基于DBSCAN密度聚类和长短期记忆网络的同调机群辨识方法

闫 旭，薛 易，相东昊

(1.国网浙江省电力有限公司 淳安县供电公司，杭州 310000； 2.黑龙江科技大学 电气与控制工程学院，哈尔滨 150000；3.国网山东省电力公司 东营供电公司，山东 东营257000)

0 引 言

随着电网互联范围的逐步扩大，电网运行方式日益复杂多变[1]，传统电力系统暂态稳定防御体系中同调机群辨识方法，不论是在时间上还是在精度上已难以满足互联大电网在线安全稳定防控的需求[2]，亟需一种同调机群在线快速辨识的新方法，为电网调度部门采取紧急控制提供决策支撑[3]。近年来，随着广域量测系统(wide area monitoring system, WAMS)的大面积覆盖[4-5]，数据的储备容量大幅提升，电网实时量测信息得以有效采集并高效利用，为突破电力系统暂态稳定控制技术的瓶颈提供了优质的数据支撑。

随着广域量测系统的推广，发电机组电气量得以实时采集，为发电机组动态特征的提取提供了海量数据源[6]。文献[7]通过普罗尼算法提取功角信息波动特性包括幅值以及频率特征。文献[8]利用多尺度小波将功角摇摆曲线分解为整体信息和细节信息。文献[9]基于面板数据提取机组功角、机端电压及转子角速度3个指标在时间序列上不同的特征。文献[10]通过挖掘机端电压相量轨迹特性辨识同调机群。

基于同调机群辨识结果中相同簇类间的动态波动特征行为相近这一现象，对受扰系统通过聚类方法提取各发电机节点电压波动特性，以实现同调机群辨识的最终目的[11]。文献[12]结合属性阈值聚类以及密度聚类方法提升分群精度。文献[13]引入谱图聚类对描述机组间同调耦合度的同调信息无向图进行图分割，辨识机组的同调性。

上述方法辨识结束时刻，系统可能已经严重失稳，此时采取措施已错过有效控制时机。针对现有方法时效性较差的问题，该文提出同调机群快速辨识方法，如图1所示。

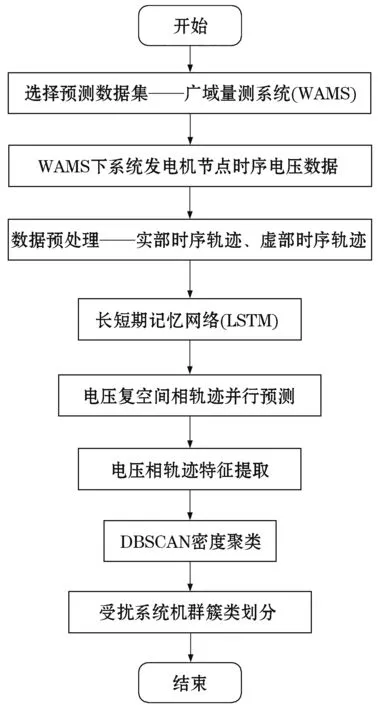
图1 电力系统同调机群快速预估方法Fig.1 Fast prediction method of coherency generator groups

基于电网积累的海量数据，结合长短期记忆网络对电网故障初期电压相量轨迹信息进行超实时预测；继而通过构建的轨迹偏移特征平面提取轨迹特征，采用密度聚类划分簇类；最后结合扩展等面积准则(extend equal area criterion，EEAC)对所提辨识方法加以验证。

1 基于长短期记忆网络的电压动态轨迹快速预测

电压相量轨迹以实虚部描述其复空间内的坐标变化情况，以图2所示等值2机系统为例[14]，假设阻抗均匀分布，1、2、3、4、5分别为联络线上的等分点。

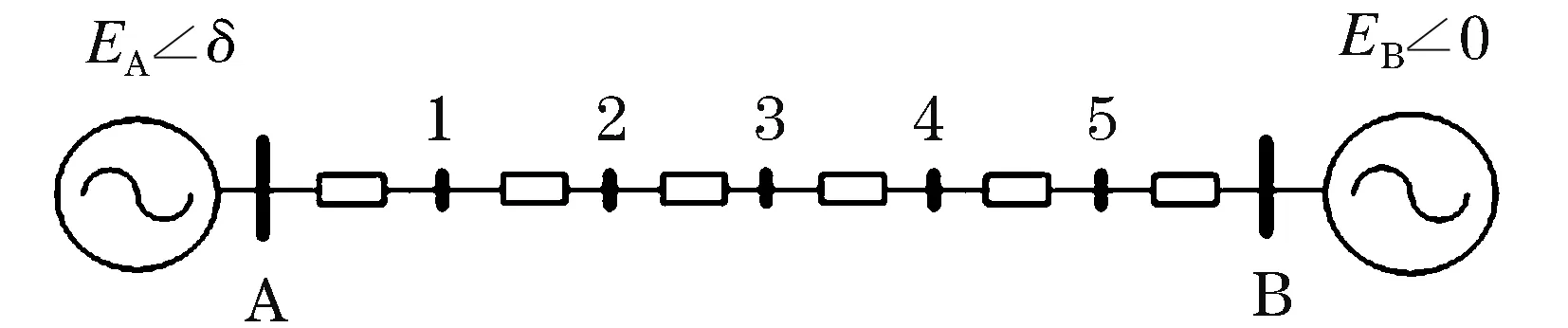
图2 电力系统2机模型Fig.2 Double machine model of power system

假设两电势幅值EA和EB相等，δ在0°～360°范围内变化，各节点的电压相量轨迹是半径不同的圆，如图3所示。

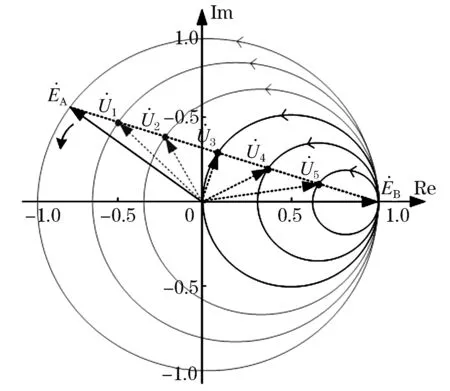
图3 节点电压相量轨迹Fig.3 Nodal voltage phasor trajectory

如直接对电压相量轨迹进行预测，由于缺失时间属性的参与，必定会降低预测精度，因此对电压相量轨迹进行拆分，如图4～5所示，通过长短期预测方法并行预测带有时间属性的电压相轨迹实虚部，该方法相较于直接预测方法可有效提升轨迹预测精度。

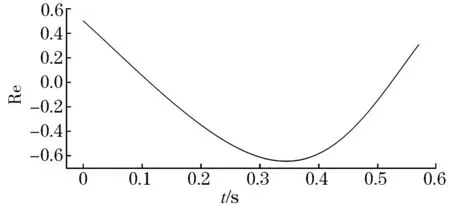
图4 相轨迹实部时序轨迹Fig.4 Real part trajectory of phasor trajectory

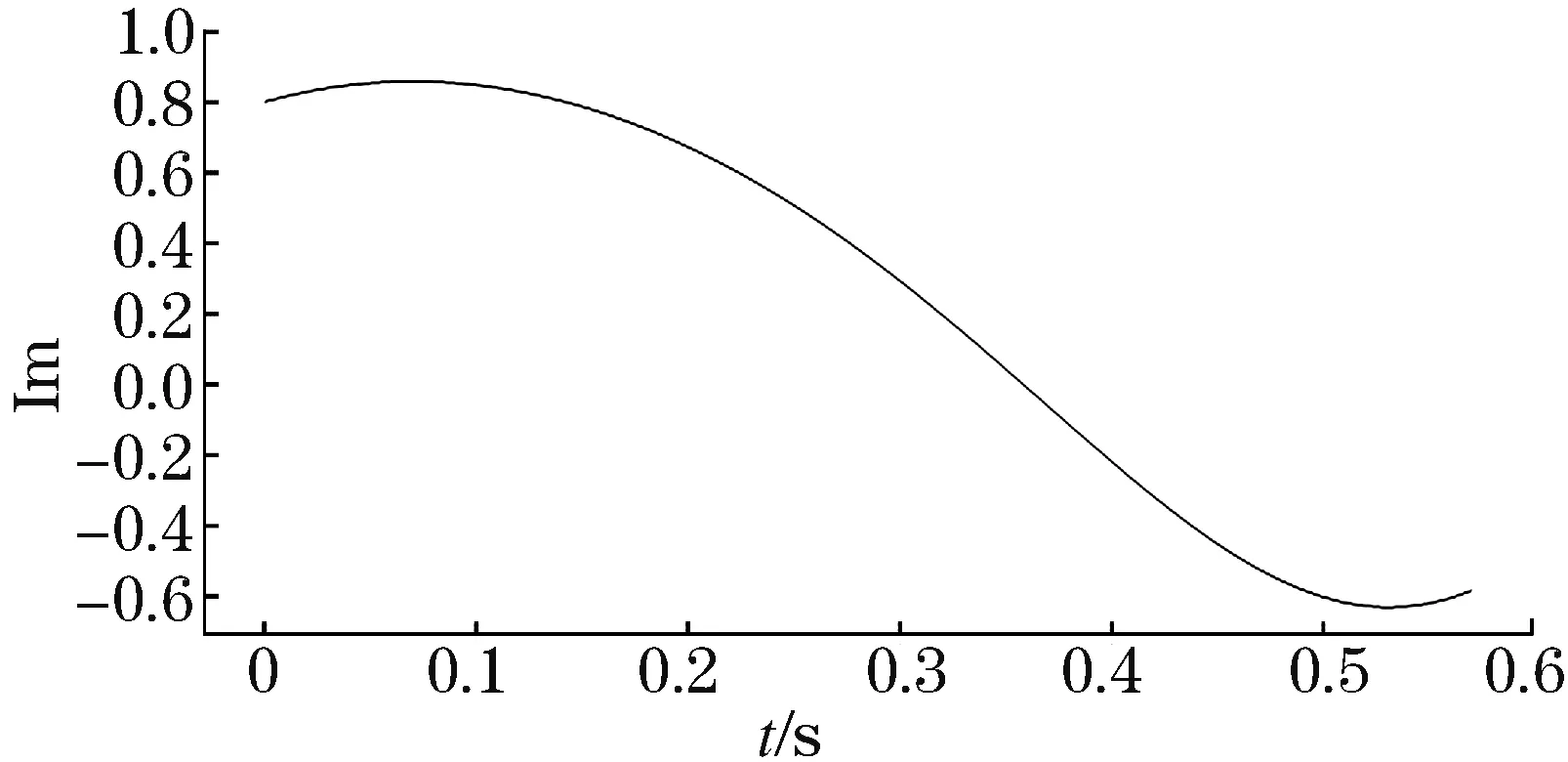
图5 相轨迹虚部时序轨迹Fig.5 Imaginary part trajectory of phasor trajectory

为提升预测精度，长短期记忆网络充分考虑时间属性的影响，并通过门控制器强化记忆。多时间断面下的非线性拟合问题可以显著提升数据预测精度，有效解决互联大电网具有多源信息交互的数据预测问题。

长短期记忆网络出色的记忆功能主要由其内部的LSTM记忆单元实现。图6所示为长短期记忆网络记忆单元的内部结构示意图，单元由输入门(Input Gate)、输出门(Output Gate)、遗忘门(Forget Gate)组成，且添加了一条用以长期记忆信息的信息链，保证关键特征信息能够有效记忆、迭代、传递。

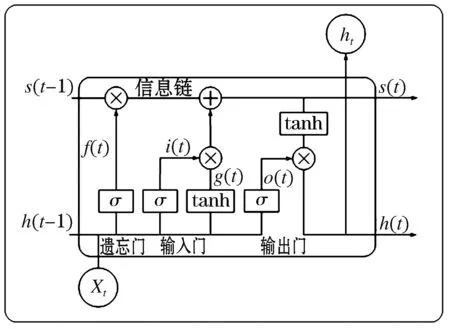
图6 LSTM记忆单元内部示意图Fig.6 Internal schematic diagram of LSTM memory unit

如图6所示，记忆单元不同的“门”控制器内部由相应的激活函数对输入信息进行“审核”，详细过程为：输入信息同前一时刻隐含层的输出同时通过记忆单元内部遗忘门、输入门、输出门，并通过对应的激活函数。从图6中可以看出，信息链上的信息汇集功能主要由遗忘门与输入门参与实现，信息于信息链上汇集后经在激活函数与输出门的共同作用得到当前时间断面下记忆单元的输出结果，具体计算式如下所示：

i(t)=σ(Wixx(t)+Wihh(t-1))+bi

(1)

f(t)=σ(Wfxx(t)+Wfhh(t-1))+bf

(2)

o(t)=σ(Woxx(t)+Wohh(t-1))+bo

(3)

s(t)=g(t)·i(t)+s(t-1)·f(t)

(4)

(5)

(6)

式(1)～(4)分别代表输入门、遗忘门、输出门、信息链对应的计算式。其中，Wih、Wfh、Woh为各门控制器与输出信息间的权重关系；Wix、Wfx、Wox分别表示各门控制器与输入信息间的权重关系；bi、bf、bo分别表示各门控制器的偏置向量。式(5)～(6)对应门内激活函数，主要为sigmoid以及tanh函数。

3个门控制器的共同作用实现了输入信息的遗忘与记忆功能，并通过专门的信息链保证关键信息有效传递。针对现今具有高维时变非线性特点的电网数据而言，长短期记忆网络可以有效挖掘蕴含在电网数据中的关键特征并长时间记忆，具有较好的工程实用价值。

电压相量轨迹如图7所示，G1～G5代表同一时间段内电压相量轨迹曲线。可以看出，该时间段内电压相量轨迹间波动异性随时序演进而逐渐显现。该文通过构建特征偏移平面提取轨迹偏移特征，为后续通过DBSCAN密度聚类辨识同调机群提供前期数据准备。

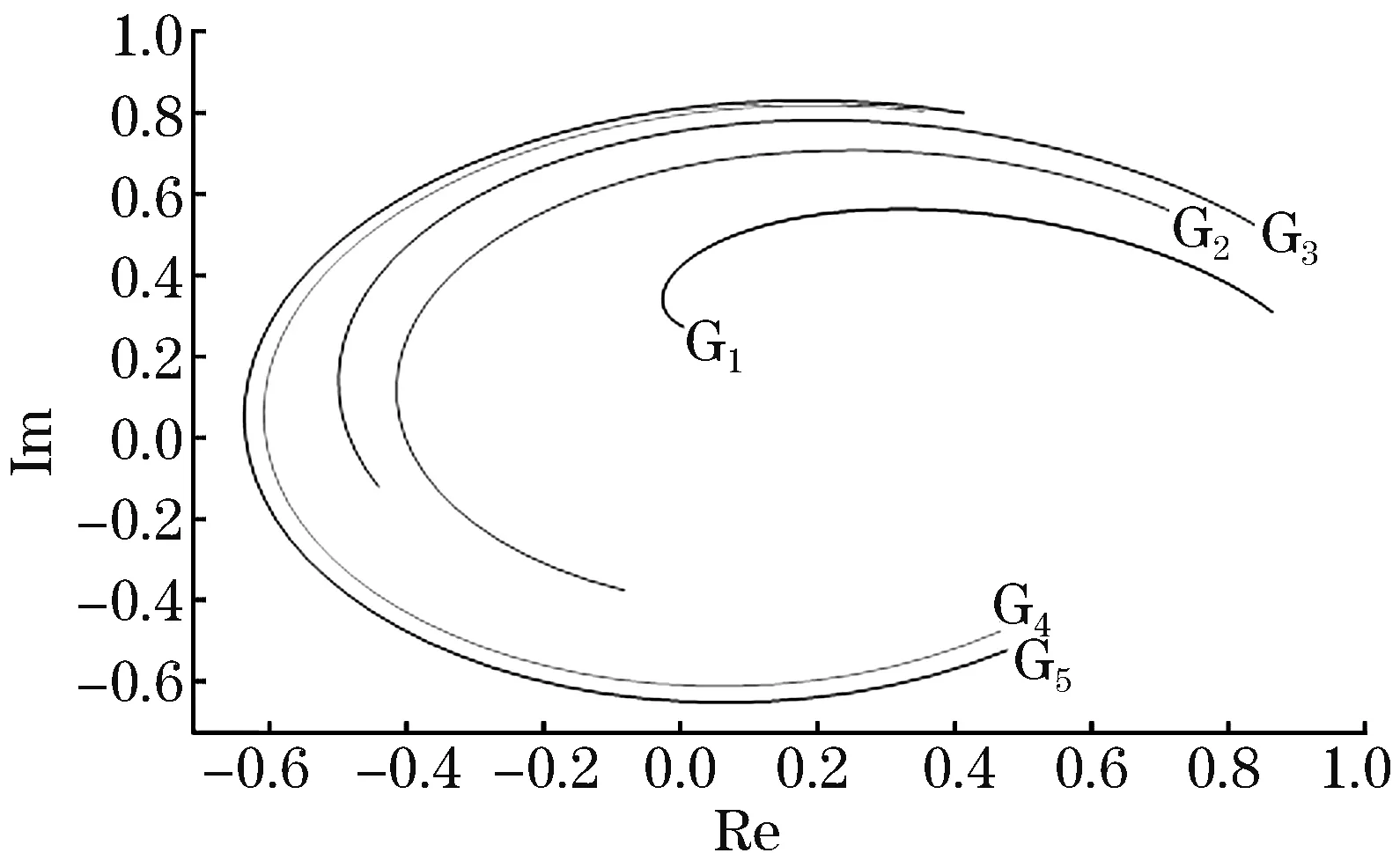
图7 电压相量轨迹Fig.7 Voltage phasor trajectory

2 基于DBSCAN密度聚类的电网同调机群快速辨识

多机系统中机组间存在着不同程度的耦合关系，扰动发生后，电网内的发电机组将呈现明显的振荡分群现象。同属一群的发电机组，其机端电压相轨迹的偏移趋势具有强相似性，而分属两群的发电机组，其机端电压相轨迹偏移具有较大的差异性。因此如何提取能够反映系统分群特性的轨迹特征是同调机群快速辨识的关键。

2.1 轨迹偏移特征平面的构建

电网节点电压运动的相似性特点使邻近机组的轨迹信息具有局部相似性与整体差异性特点。从运动学角度看，轨迹变化趋势可用相邻相量间的转角、长度加以表征[15]。因此，通过挖掘电压相轨迹的几何特征，可以实现对受扰系统内节点的快速聚类。基于此，构建了轨迹偏移特征平面，具体如图8所示。

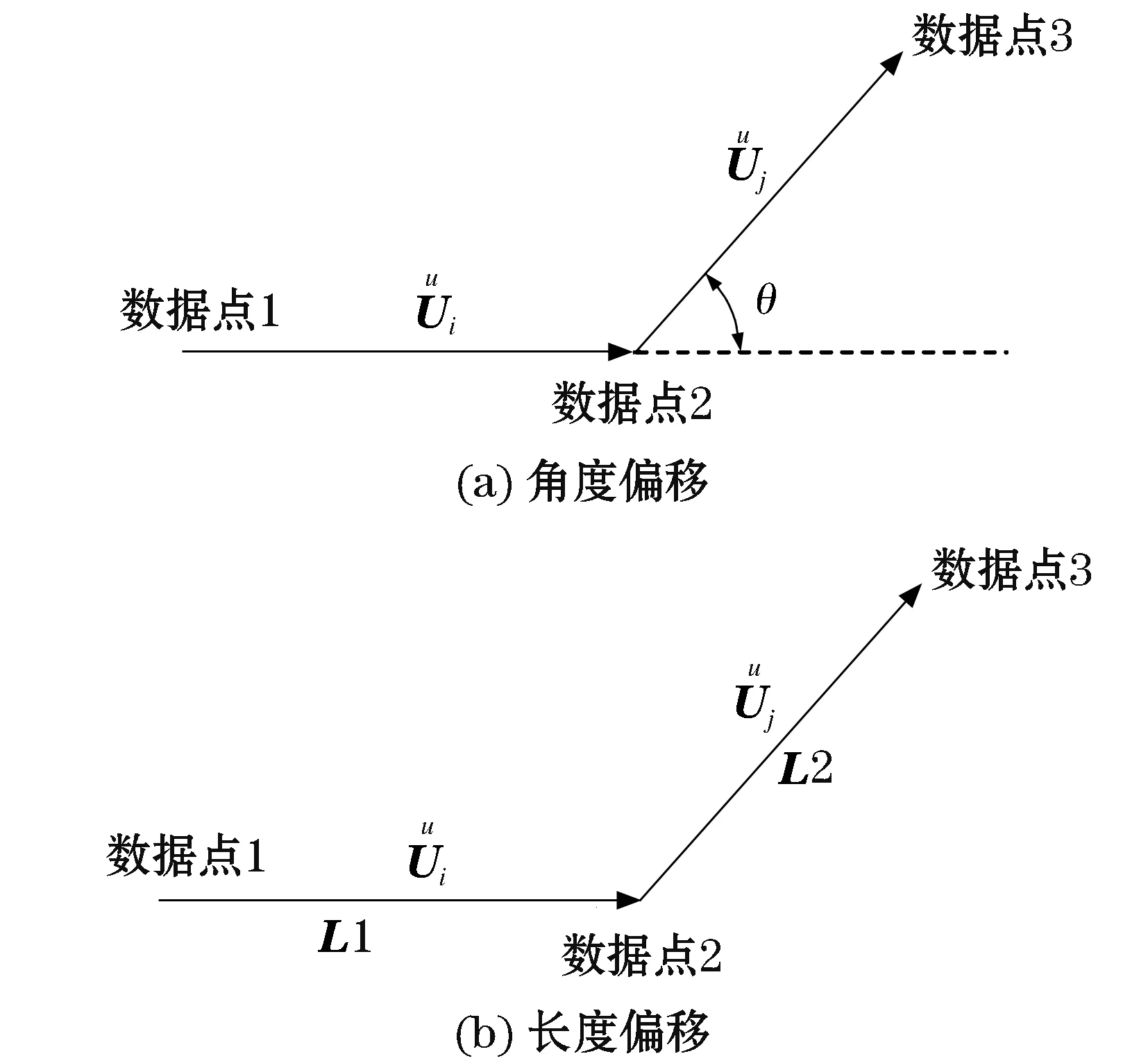
图8 轨迹向量偏移Fig.8 Trajectory offset

(7)

长度偏移定义如式(8)所示：

(8)

长度偏移与角度偏移对应的值越大，代表相邻时间断面内不同发电机组电压相轨迹间的关联性越小，属于同一簇类的概率就越低。

如图9所示，相邻时间断面内的电压相量轨迹运动规律可以长度偏移与角度偏移为载体体现。采用DBSCAN密度聚类将不同电压相轨迹的长度偏移与角度偏移作为坐标点进行聚类分析，由于轨迹波动特征悉数提取，聚类效果也更为明显。

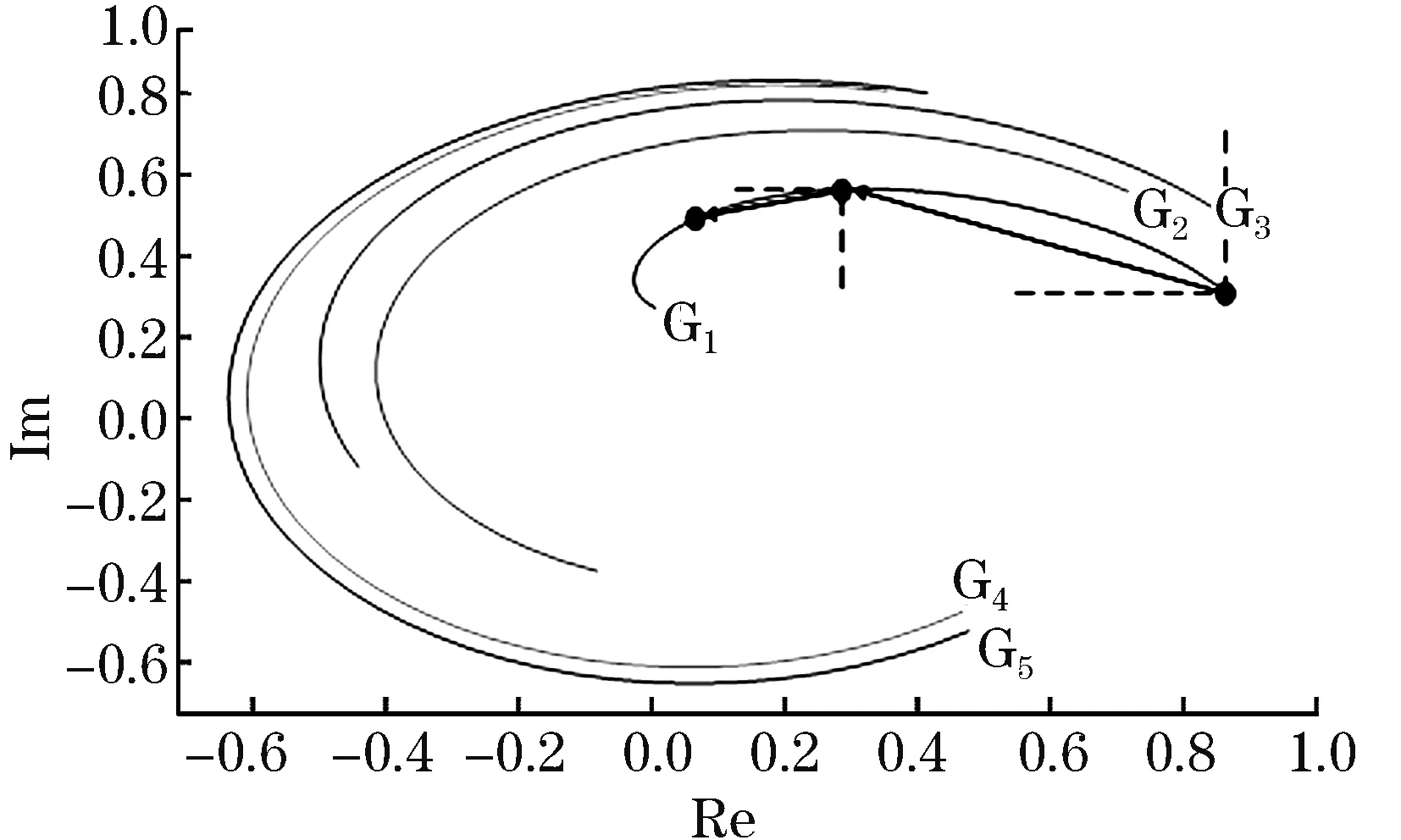
图9 轨迹偏移Fig.9 Trajectory offset

2.2 DBSCAN密度聚类的算法原理

作为无监督学习的重要技术手段，DBSCAN密度聚类的实质是甄别样本数据集中的高密度数据集合并进行划分处理，基于密度可达关系确定最大密度相连的样本群。同其他的聚类方法有所不同，DBSCAN密度聚类可以实现对任一复杂数据确定聚类数并进行聚类处理，同时对数据中的噪声点进行辨识并加以剔除。

DBSCAN密度聚类方法引入Eps邻域与邻域密度阈值min Pts参数确定划分高密度数据集合的阈值，其中Eps邻域代表聚类类簇的半径值大小，min Pts定义聚类类簇所含样本数。Eps邻域：若存在数据集D，其内xi样本的Eps邻域是指规定半径内的样本集。具体定义式为

NEps={xi=D|distance(xi,xj)<=Eps}

(9)

对任一样本数据集D=(x1，x2，x3，…xn)，有关其聚类过程除上述Eps邻域以及min Pts邻域密度阈值外共涉及如下参数：

1)核心对象：假设样本数据xj∈D，且其Eps邻域内所涉及样本点不小于邻域密度阈值，算式为

|N(xj)|≥min Pts

(10)

即表明点xj为核心对象。

2)密度直达：样本数据xj同其Eps邻域内任一点间存在密度直达关系。

3)密度可达：对于样本序列{n1，n2，n3，…nn}，xi=n1，xj=nn，nn+1同nn之间密度直达，则xi同xj之间亦可成为密度可达关系。

4)密度相连：同样对于样本数据集D，其中样本点x3为核心对象，如果x1、x2同x3之间同时存在密度可达关系，则x1、x2密度相连。

为详细说明，通过图10演示DBSCAN密度聚类分群原理：对任意规模样本集进行聚类，设定min Pts为5，图10中空心点代表核心对象，实线圆内的点代表同核心对象间存在密度直达关系的样本集合，核心对象间的箭头则代表核心对象间存在密度可达关系，以此可以得到样本数据集的分群处理结果。

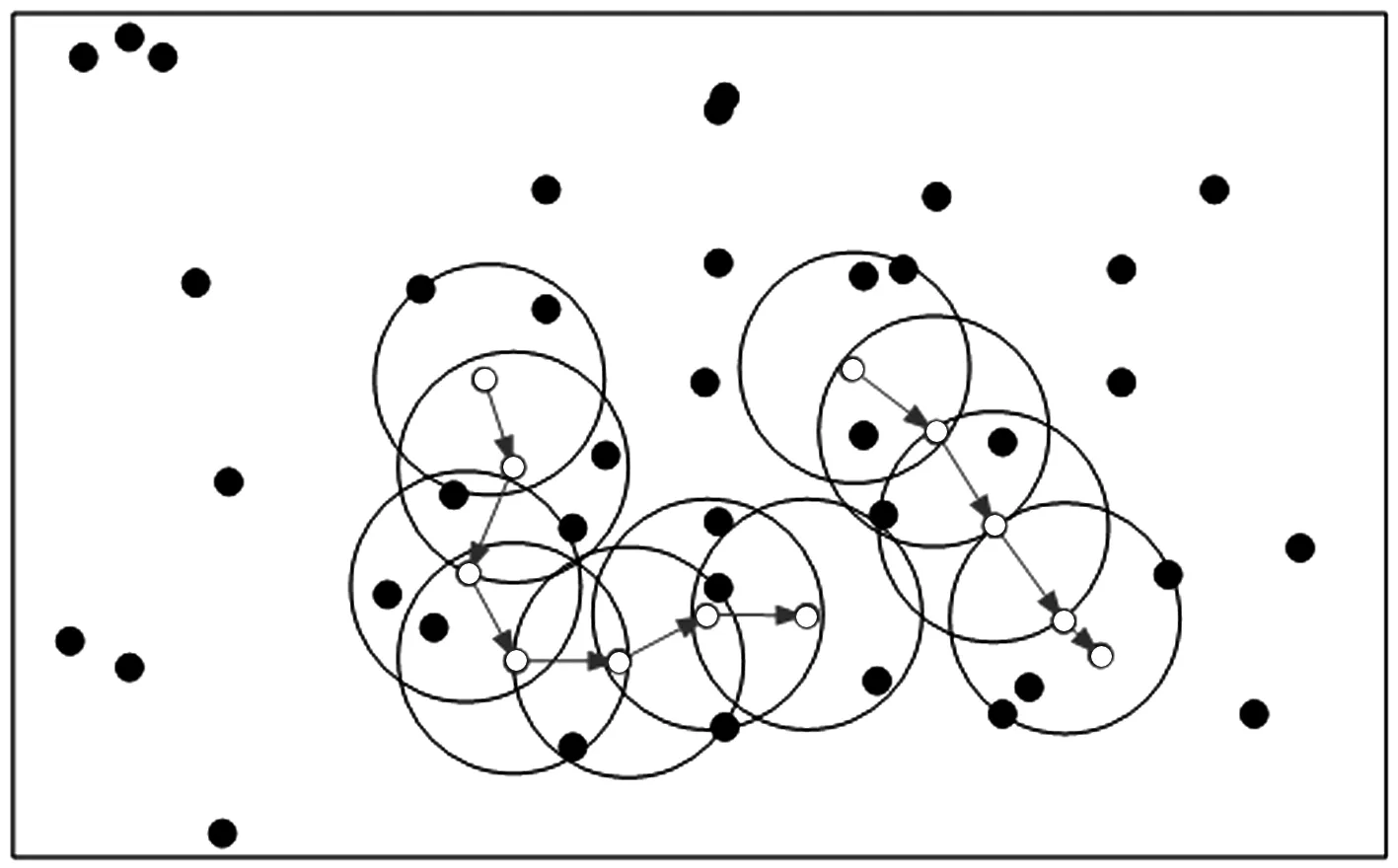
图10 DBSCAN聚类示意图Fig.10 DBSCAN clustering diagram

3 基于EEAC的同调性辨识结果验证

基于EEAC[16]对上述基于DBSCAN密度聚类预测的同调机群辨识结果进行校核。通过CCCOI-RM变换，得到领先群S和滞后群A的等值单机映像，定义如下：

(11)

式中：M为等值惯量；δ为等值功角；ω为等值转速；PM为等值机械功率；PE为等值电磁功率。上述各变量计算如下式所示：

δ=δS-δA

(12)

ω=ωS-ωA

(13)

(14)

(15)

(16)

式中：MS、PMS、PES分别为超前机群内等值惯量、等值机械功率、等值电磁功率；MA、PMA、PEA分别为滞后机群内等值惯量、等值机械功率、等值电磁功率；δS和δA分别为S和A的功角；ωS和ωA分别为S和A的转速。图11为在稳定和失稳情况下基于上述模型得到的S和A等值功-角特性曲线。

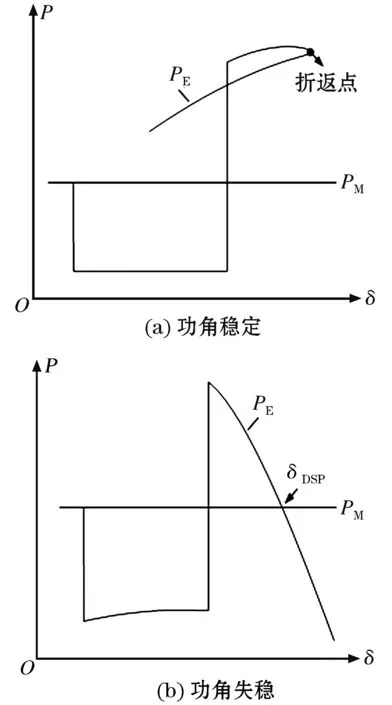
图11 功-角特性曲线Fig.11 P-δ curve

图11(a)中等值功角在抵达折返点后开始回摆，功角开始减小，表明S和A保持同步维持稳定，同调性好；由图11(b)可知，等值功-角特性会越过动态鞍点(dynamic saddle point, DSP)，功角继续增大，表明S和A失去同步无法稳定，同调性差。

4 算例分析

通过IEEE-39节电系统对所提同调机群辨识方法加以验证，通过仿真获得所需样本数据集。系统拓扑如图12所示，其中包含10台发电机，39号母线上的发电机代表与该系统相连的外部电力网络。

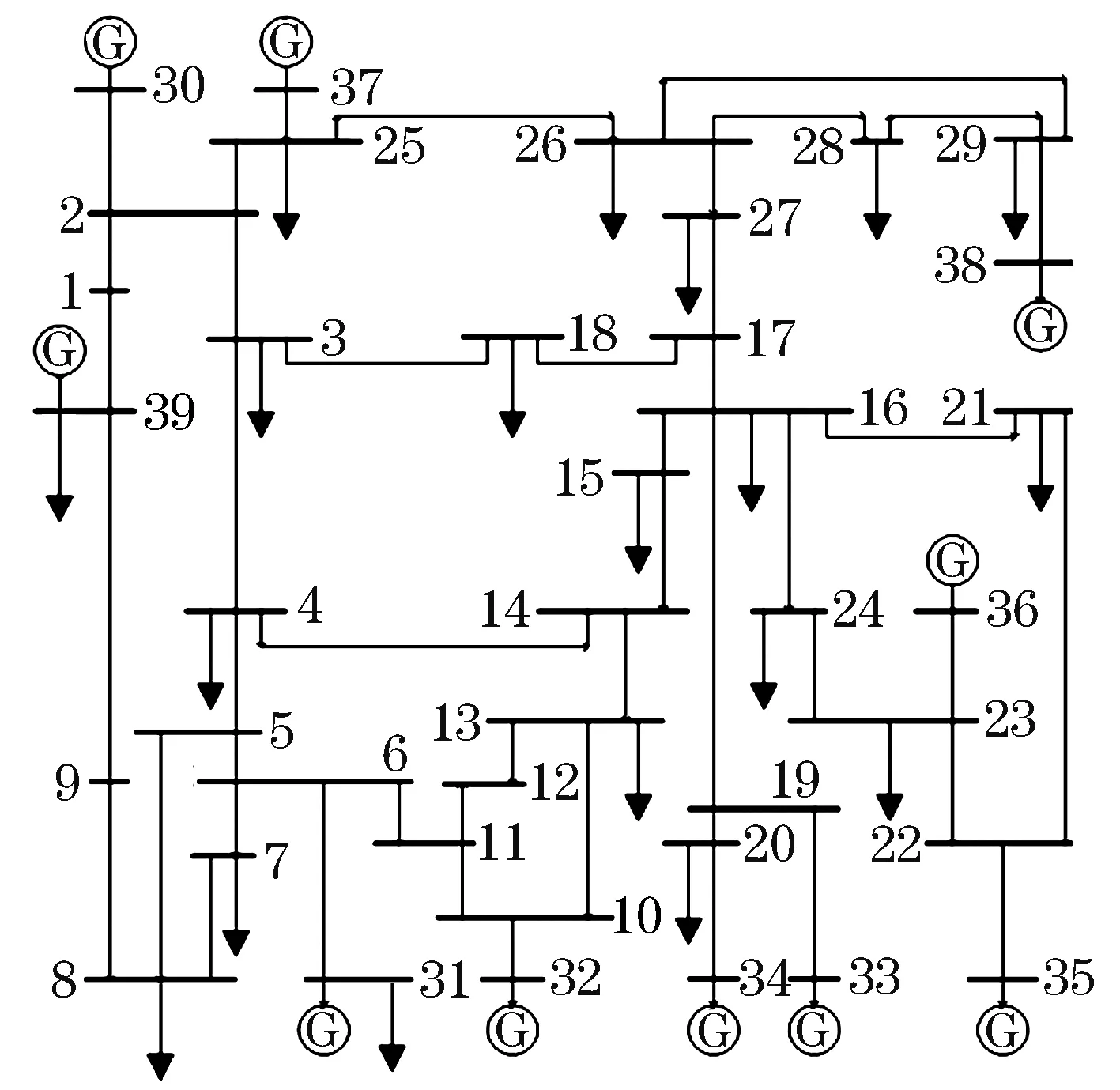
图12 IEEE-39节点系统拓扑Fig.12 IEEE-39 bus system topology

有关长短期记忆网络预测模型搭建以及训练学习过程采用Python编译软件实现，利用其搭建长短期记忆网络模型并进行超实时预测，有关长短期记忆网络记忆单元的参数设置见表1。

表1 记忆单元参数Table 1 Memory unit parameter

如表1所示，反复试验后确定LSTM记忆单元采用sigmoid激活函数，以均方根误差函数以及RMSprop优化算法核定预测精度，不断迭代并校正预测结果。

根据系统的故障位置以及故障清除时刻的不同，构建长短期记忆网络的学习样本共12 000组，随机抽取10 000组用以训练，其余作为测试样本。采用均方根误差算法在迭代过程中对预测值进行修正，结果如表2所示。

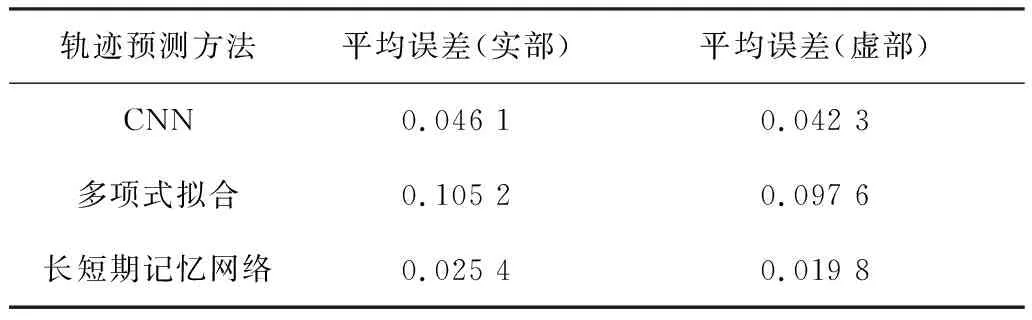
表2 电压相轨迹预测效果对比Table 2 Comparison of prediction effect of voltage phase trajectory

由表2可以看出，长短期记忆网络的预测结果的平均误差均小于另2种方法，表明预测样本与实际样本间的离散程度最低，即代表该方法非线性拟合的效果最好。

通过总结分析发现，系统失稳初始状态多为两群失稳模式，若未采取有效控制手段，大多将发展为多群失稳模式。因此采用两群失稳样本进行研究，设定t=0 s时在线路16—24的50%处发生三相短路故障，0.22 s后清除，系统38号机为领先机组，其余机组为滞后机组，功角变化曲线如图13所示。

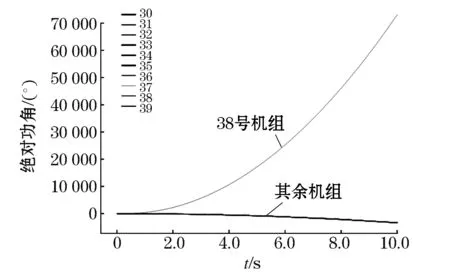
图13 IEEE-39节点系统功角曲线Fig.13 P-δ curve of IEEE-39 bus system

基于广域量测系统采样周期值大小，以故障清除后的采样点作为待预测样本数据，设置时窗步长为1，时窗长度为7，通过长短期记忆网络对电压相量轨迹进行预测，结果图14所示。

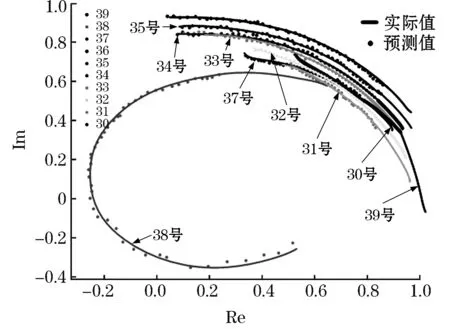
图14 各机组仿真结果曲线Fig.14 Simulation result curve of each curve

根据所提同调机群快速辨识体系方法，基于长短期记忆网络预测对受扰系统电压相轨迹信息进行快速预测，继而根据轨迹偏移特征平面对电压相轨迹波动特征进行提取，并通过DBSCAN密度聚类快速预测同调机群，根据反复试验最终确定Eps邻域值为0.12，min Pts值为1，最终聚类结果如图15所示。

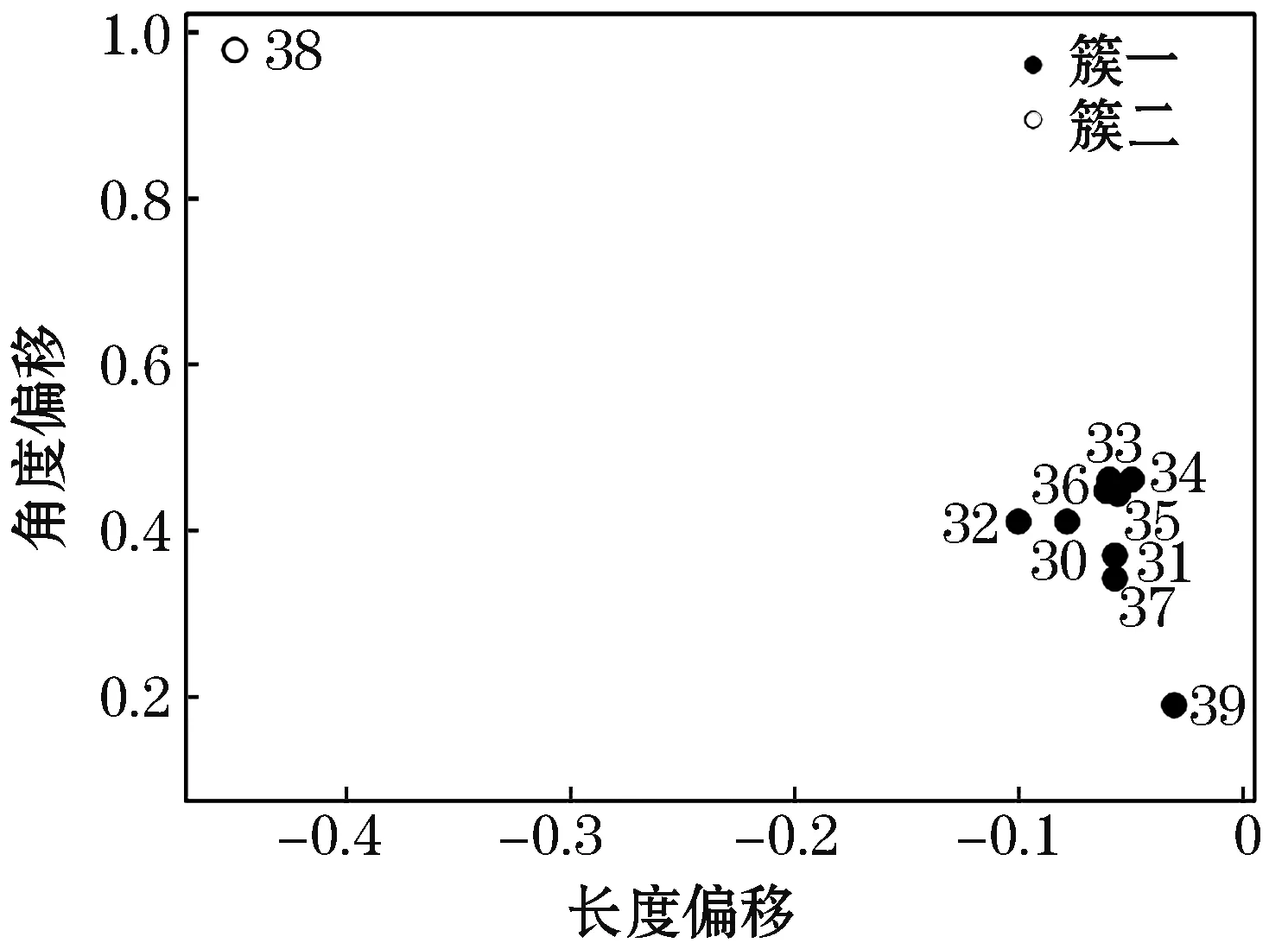
图15 聚类分析Fig.15 Cluster analysis

图15所示为聚类分析效果图，领先机群与滞后机群间的电压相轨迹偏移差异明显。其中，发电机38为一簇，其余机组相轨迹成簇，通过比对功角大小划分发电机38归属领先机组，其余归属滞后机组，结果如表3所示。

表3 分群结果Table 3 Clustering results

利用EEAC对上述辨识结果进一步验证，领先群S和滞后群A的等值功-角特性曲线如图16所示。

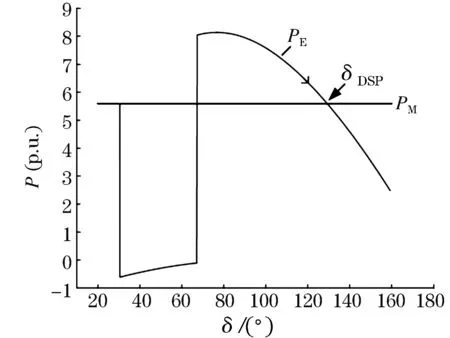
图16 功-角特性曲线Fig.16 P-δ curve

当t=0.54 s时，等值功-角特性越过DSP，功角持续增大，表明S和A两机群失去同步无法稳定，验证了所提方法分群结果的准确性。

5 结 语

1)通过长短期记忆网络对受扰后的电压相量实虚部时序轨迹并行预测，相比其轨迹预测方法，具有更高的预测精度。

2)构建轨迹偏移特征平面，提取出电压相量轨迹信息的时序变化特征，为同调机群快速辨识提供新途径。

3)基于DBSCAN密度聚类方法进行轨迹时序变化特征的聚类分析，并通过EEAC校核聚类结果，进而实现同调分群。该方法不依赖于模型，具有较好的泛化能力。