长眼轴白内障眼六种人工晶体度数计算公式的准确性分析

杨 智 史庆成 吴海娟 周衍文▲

1.沈阳爱尔眼视光医院白内障科，辽宁沈阳 110003；2.辽宁省康平爱尔眼科医院综合眼病科，辽宁康平 110500

高度近视已经成为全球范围内发病率越来越高的公共健康问题，尤其在亚洲[1]。眼轴超过26 mm的高度近视白内障患者逐渐增多。第二、三代及部分第四代人工晶体（intraocularlens，IOL）度数计算公式对于正常眼轴眼的预测准确性尚可,但是对于长眼轴眼,预测误差增大并向远视飘移[2-4]。对于这种误差的矫正有几种方法，包括Wang-Koch眼轴矫正公式、IOL常数优化、使用新一代公式等，但是眼轴矫正计算相对繁琐，而仅针对长眼轴的个性化的常数优化并不优于ULIB网站上的优化方法[5]。目前国际上出现很多新的准确性更高的公式：包括 Kane[6]、Hoffer QST[7]、Barrett UniversalⅡ[8]等，大多能在网上免费获得。本研究观察不同公式在长眼轴眼的IOL度数计算方面的准确性。

1 资料与方法

1.1 一般资料

回顾性分析2019年3月至2020年3月沈阳爱尔眼视光医院收治的44例（44眼）长眼轴（＞26 mm）的白内障患者临床资料，所有患者接受白内障超声乳化术（或者飞秒激光辅助）联合IOL植入术。其中男15 例，女 29 例；年龄 25～79 岁，平均（57.7±11.0）岁；病程2～36个月，平均7（2，11.5）个月。本研究已经沈阳爱尔眼视光医院医学伦理委员会审核批准。

纳入标准：①全部患者眼轴＞26 mm，平均眼轴（30.45±1.82）mm；②晶状体混浊程度依据 LOCSⅢ系统分级[9]，皮质混浊小于C4，核混浊小于N4，后囊下混浊小于P3。

排除标准：①角膜云翳影响角膜曲率测量；②翼状胬肉侵入角膜超过1 mm；③严重晶体混浊不能用IOL Master测量获得眼部数据；④各种类型青光眼；⑤既往眼部手术史；⑥严重眼底病变；⑦术中及术后发生手术相关的并发症；⑧术后最佳矫正视力＜0.5。

1.2 方法

术前常规行眼前节裂隙灯显微镜检查、眼底检查、A超、B超、眼压、电脑验光、角膜地形图以及角膜内皮镜检查等。使用用IOL Master700(德国Carl Zeiss公司)测量眼轴长度（axial length，AL）、角膜曲率（ker atometry，K）、前房深度（anterior chamber depth，ACD），晶体厚度（lens thickness，LT），白到白（white to white，WTW）等数据。通过IOL Master700内置的SRK-T、Hoffer Q和Holladay2公式以及在线计算公式Barrett UniversalⅡ、Kane、Hoffer QST，计算所用 IOL 的度数和预期屈光度，最终IOL度数主要参考Barrett UniversalⅡ和Kane公式，并预留-0.5 D左右。

手术由同一位资深医师进行，采用2.2 mm 120°角膜缘切口，植入可折叠式后房型IOL（德国人类光学非球面晶体，MCX11 ASP）于囊袋内，光学面居中。A常数采用厂商建议常数118.3（因ULIB网站并无该晶体优化常数）。

1.3 观察指标及评价标准

术后1个月复查时进行电脑验光及主观验光，综合得到患者最佳视力的等效球镜度，用实际术后屈光度减去预期屈光度得到的数值的绝对值做为绝对屈光度误差（absolute refractive error，AE），其中位数为中位绝对屈光度误差（median absolute refractive error，Med AE）。计算并比较各公式的Med AE、ME以及各公式在0.5 D及1.0 D误差范围内的比例。

1.4 统计学方法

采用SPSS 20.0统计软件进行数据分析，符合正态分布的计量资料用均数±标准差（±s）表示，两组间比较采用t检验，不符合正态分布者转换为正态分布后统计学分析；计数资料采用率表示，组间比较采用χ2检验，以P＜0.05为差异有统计学意义。各公式Med AE比较采用Friedman秩相关样本的双向方差分析并进行两两比较，以P＜0.05为差异有统计学意义。

2 结果

六种公式的绝对预测误差比较，差异有统计学意义（χ2=175.36，P＜0.05）。各公式 Med AE 及 ME 见表1，可见各公式在长眼轴眼预测误差普遍向远视飘移。Kane、Barrett UniversalⅡ、Hoffer QST、SRK-T、Holladay2、Hoffer Q公式误差在0.5 D以内的比例分别为36.4%、27.3%、22.7%、9.1%、4.5%、4.5%，误差在 1.0 D以内的比例分别为70.5%、63.6%、50%、31.8%、11.4%、9.1%。可见Kane公式和Barrett UniversalⅡ公式以及Hoffer QST公式误差绝对值最小，较低误差所占的百分比最大。

表1 六种公式Med AE及ME比较（D，±s）

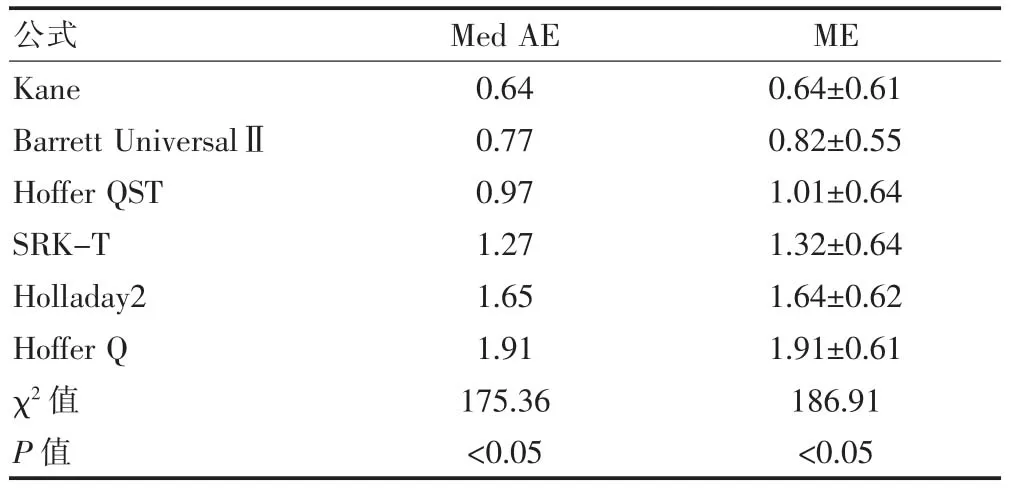
表1 六种公式Med AE及ME比较（D，±s）

公式 Med AE ME Kane Barrett UniversalⅡHoffer QST SRK-T Holladay2 Hoffer Q χ2值P值0.64 0.77 0.97 1.27 1.65 1.91 175.36＜0.05 0.64±0.61 0.82±0.55 1.01±0.64 1.32±0.64 1.64±0.62 1.91±0.61 186.91＜0.05

3 讨论

Kane公式[6]由Jack X Kane研发，其基于理论光学原理并加入人工智能因素，但是其公式结构尚未公布，该公式可在网站http：//www.iolformula.com获得（于2020年2月16日发布）。它使用角膜曲率、眼轴、前房深度、性别来预测有效IOL位置 （effective lens position，ELP），角膜厚度和晶体厚度为可选项，越来越多的研究证实该公式准确性位于前列[10-13]。

Barrett UniversalⅡ公式由Graham Barrett在其1987年研发的一代公式基础上不断改进而来，2013年更名为Barrett UniversalⅡ公式。为厚透镜公式，基于近轴光线追迹技术。其使用眼轴、角膜曲率和前房深度预测ELP，晶体厚度和角膜直径做为可选项。已经有很多大样本研究证实其准确性[14-15]。

Hoffer QST公式由Hoffer等在Hoffer Q公式基础上完善而来，可在网站http：//www.hoffer qst.com.免费获得[7]。

本研究纳入44例患者共44只长眼轴眼（平均眼轴为30.45 mm），回顾性比较了六种公式的准确性。按照国际上目前通行做法[10]，主要比较Med AE的大小以及在误差在0.5 D及1.0 D以内的比例。研究发现六种公式准确性依次为Kane、Barrett UniversalⅡ、Hoffer QST、SRK-T、Holladay2、Hoffer Q 公式，但前三者间差异无统计学意义，与Kane等[6]的研究结果相似。不过在一定误差范围内的患者比例，仍然是Kane公式最高，Barrett UniversalⅡ公式次之。同时，通过比较ME，发现在长眼轴眼中，各公式都不同程度的存在远视飘移。本研究结果，对于长眼轴眼IOL度数预测，应以Kane、Barrett UniversalⅡ等新一代公式为主，同时根据眼轴长度预留一定度数的近视，以达到术后正视。目前国内尚无关于Kane公式、Hoffer QST公式应用于超长眼轴眼（平均30.45 mm）的准确性研究。

本研究的局限性在于样本量偏小，同时未进行A常数优化，有待今后增加样本量，并进行常数优化后再行比较。另外对于预留近视的量，尚无量化方法，有待于今后更大样本的长眼轴数据（≥26 mm）分析，通过建立回归方程的方法，优化各公式的预留量。同时对Kane公式、Hoffer QST公式应用于中国人正常眼轴和短眼轴眼的准确性做进一步观察。

综上所述，对于高度近视白内障患者的IOL度数计算，建议选择Kane公式和Barrett UniversalⅡ公式，同时因为所有公式均向远视飘移，可根据眼轴预留一定度数的近视。