基于思维水平促进学生空间观念发展的数学活动设计
2021-12-29陈春芳
□陈春芳
通过数学教学活动,帮助学生积累数学基本活动经验,是义务教育阶段数学教学的核心目标之一。义务教育阶段,学生在“图形与几何”领域学习的主要内容是直观几何。教师需要通过设计一系列活动帮助学生积累活动经验,建立空间观念。
教师在设计数学活动时不仅要充分利用学生已有的知识与经验,还要考虑学生几何学习的思维特点。20世纪50年代,荷兰学者范希尔夫妇把几何思维划分为5个水平:直观水平、分析水平、非形式化的演绎水平、形式化的演绎水平和严密性水平。这一几何思维发展理论认为,几何学习不是一个连续的过程,而是跳跃的分阶段的过程,上述5个思维水平之间存在次序性。为了帮助学生从一个水平过渡到下一个水平,数学活动扮演着极其重要的角色。在设计数学活动时教师要特别关注学生的几何思维水平是怎样的,学生的认知困难在哪里,在此基础上设计符合学生认知规律和思维水平的数学活动,发展学生的空间观念。
一、设计实物与图形相互转化的数学活动
在对“空间观念”进行描述时,“想象”一词非常重要。心理学把人对头脑中已有表象进行改造,创造出新形象的过程称作想象。没有想象,很难对现实世界进行了解与把握,很难做到发明与创造,因此发展学生的空间观念要重视对想象能力的培养。教学中,教师要注重在实物与图形之间搭建桥梁,设计物与形联系的数学活动,在想象中培养学生的空间观念。
(一)在从实物到图形的抽象活动中培养空间观念
经历从实物中抽象出几何图形的过程,是学生发展空间观念的第一步。如在教学“长方体和正方体的认识”时,教师请学生在课前收集了很多外形是长方体或正方体的物品,包括茶叶盒、香皂盒、礼品盒等,课堂上教师通过动画演示将包装盒的颜色、装饰等去除,引导学生充分关注物品的形状、大小,帮助学生将自己展示的物品抽象成与之对应的立体图形。在这一过程中,学生的思维逐渐由实物直观过渡到图形直观,最终发现长方体图形的本质属性,发展了空间观念。
(二)在借助图形推想实物的活动中培养空间观念
学生的几何思维在图形直观的基础上进一步发展,将达到想象直观水平。教学中,教师要设计能帮助学生借助想象发展空间观念的活动。如呈现立体图形的三视图及相关的数据(如图1),请学生借助信息想象图形,并猜测可能是什么物体。

图1
在猜测过程中,学生根据空间知觉得到初步判断:长10米的物体,肯定不是家用冰箱。那么,长10米的物体可能是什么?首先,学生想到测量教室的大小,教室的长大约是8米,宽大约是6米,高大约是3米。其次,借助教室的表象,再次想象三视图中所描述的物体的大小,发现其长与教室的长差不多,宽比教室的一半还小,高和教室的高度相差不大。从而想象出三视图所描述图形的原型,可能是公共汽车。在这个过程中,学生由开始的空间知觉,到借助教室大小形成空间表象,最后在与教室大小的比较中想象出三视图描述的物体的大小,即形成空间观念。这一从知觉到表象再到合理想象的递进发展过程,培养了学生的空间观念。
二、设计操作与想象相互结合的数学活动
小学生形成、发展空间观念主要依靠“视”与“触”。在整个小学阶段,触觉、运动觉与视觉的协同活动,始终是学生获得空间观念的有力支撑。
(一)基于学情,在分类活动中建立对几何概念的直观理解
借助分类活动辨析图形特征,是学生发展空间观念的有效方式之一。如在教学“平行四边形的认识”时,教师设计了让学生将图形进行分类的活动,引导学生在观察对比的过程中感悟平行四边形、梯形等图形之间的关系。在分类对比活动中,学生逐步借助直观发现了平行四边形区别于其他图形的本质特征,加深了对平行四边形的认识。
(二)把握核心,在开放性活动中抽象出立体图形的本质特征
开放性活动有助于学生更好地把握图形的核心要素,抓住图形的本质特征。仍以“长方体和正方体的认识”教学为例,长方体是学生从抽象的角度认识的第一个三维图形,学生要由对二维图形特征的认识过渡到对三维图形特征的认识。随着图形维度的增加,学生对图形特征的探索从长、宽拓展到长、宽、高以及面,并且在头脑中逐步建立起对立体图形各要素之间关系的理解。
教学时,教师为每个小组提供了不同规格的学具,请学生尝试选择学具拼搭长方体。学生需要根据各学具袋中给出的小棒长度和数量(如表1),先想象所拼成的长方体的样子,再动手操作拼搭长方体。
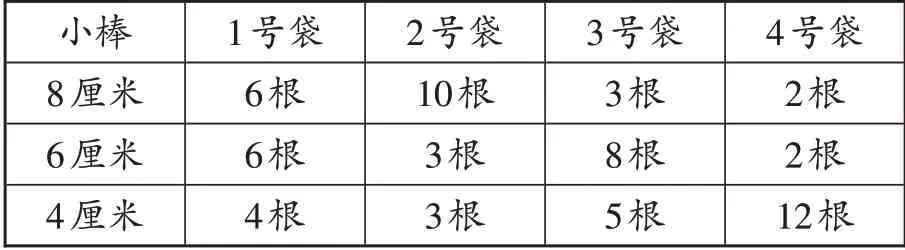
表1“拼搭长方体”学具袋材料说明
从如下课堂教学片段中可以发现,在拼搭的过程中,学生需要观察学具袋中每类小棒的长短和数量,通过不断将实物与头脑中想象的图形对接,逐步建立长、宽、高三个要素之间的联系。
生:我们组选择的是1号学具袋中的小棒。我们发现4厘米的小棒根数最少,有4根。8厘米长的小棒和6厘米长的小棒都比4根多。于是我们每一种长度选择4根,作为长方体的长、宽、高,就拼成了一个长方体。
生:我们组选择的是3号学具袋中的小棒。虽然8厘米的小棒不够4根,不能选择,但6厘米的小棒数量是8根,4厘米的小棒够4根,这样我们组拼成对面是正方形的特殊长方体。
生:我们组选择的是4号学具袋中的学具,只能选择12根4厘米的小棒拼成一个棱长为4厘米的正方体。正方体也是特殊的长方体。
师:有没有哪个组选择的是2号学具袋中的学具?
(学生摇头)
师:为什么你们不选择2号学具袋中的学具呢?
生:长方体的特征是长、宽、高各有4条,也就是需要3组4根的小棒。如果是特殊的,对面是正方形的长方体,则需要一组8根小棒加上一组4根小棒。更特殊的正方体需要的是12根同样长度的小棒。而2号学具袋中的小棒数量不足,没法拼成长方体。
在选择学具拼搭长方体、正方体的过程中,学生对长方体、正方体“棱”的特征的认识逐步加深。通过开放性的操作活动,学生的空间观念得到了发展。
(三)方法习得,在数形结合的画图中培养空间观念
画图是“图形与几何”领域常规的学习方式,学生可以通过画图丰富对几何图形的认知,促进空间观念的发展。
如请学生解决这样一个问题:“有一个长方体,‘左面’是长5分米、宽6分米的长方形,‘后面’是长9分米、宽5分米的长方形,请问这个长方体‘上面’的面积是多少?”学生需要借助画图,先将只有左和后两个面的长方体部分图还原成长方体原图,再借助图形直观找到长方体“上面”的相关数据,进而找到问题的答案。在“图形与几何”领域的学习中,培养学生画图的意识与习惯,教给学生画图的基本方法,在图形直观与想象直观间搭建平台,可以有效培养学生的空间观念。
三、设计既开放又体现综合性的主题实践活动
综合性主题实践活动是为了让学生综合利用所学知识解决问题而设计的活动。同样在“长方体”相关教学中,教师设计了“制作收纳盒”的综合性活动,让学生自主设计、制作收纳盒。
在动手操作前,学生首先联系生活实际,提出制作收纳盒需要考虑的问题:收纳盒的材质、大小尺寸、摆放位置等。课堂上教师提出要求:各组制作的收纳盒将放在班级置物架上进行展览,每个小组可用的展示台面大小不超过5平方分米,并为学生提供制作收纳盒的学具(标有数据的大小不同的长方形,有的能够使用,有的不能够使用)。学生在对这些学具进行分析的基础上,根据实际情况选择材料,设计并制作收纳盒。有的小组先选择一块长方形作为长方体的底面,底面决定了拼成的长方体的长和宽,在此数据基础上选择合适的长方形作为前后面和左右面,拼成之后,再根据条件进行验证,判断是否能够放在面积是5平方分米的置物架上。也有的小组先根据材料设计方案,将不同长方形的长和宽与长方体的长、宽、高建立对应关系,再完成收纳盒的制作。还有的小组为了能制作出更符合本组设计意愿的收纳盒,选择了先在白纸上设计出收纳盒的展开图再制作。在以上过程中,学生无论采用何种操作方式,也无论最终能否成功制作出收纳盒,他们都在综合运用数学知识,在建立二维图形与三维图形各要素对应关系的过程中,加深对长方体性质、特征的理解和把握。
儿童空间观念的形成是一个渐进的过程,这个过程与儿童空间思维水平发展的阶段性相联系。“图形与几何”教学必须根据学生的认知特点和几何思维水平设计数学活动,让学生在有效的活动中积累经验,发展空间观念。
