基于SLPP-LSSVM 的空战效能评估研究

李宗晨，姚 旭，甘旭升

（空军工程大学空管领航学院，西安 710051）

0 引言

战斗机是进行空中突击的主要武器，其性能水平很大程度上反映了国家的航空科技实力。战斗机的空战效能通常是指战斗机完成预定空战任务所具有的性能和能力。空战效能评估就是从不同层面定性定量地综合描述战斗机的空战使用效能。其在战斗机研制采购、敌我双方作战实力对比、作战预案想定等方面都有广泛的应用，也可为指挥员作出进一步决策提供依据。

由于战斗机自身的复杂性以及空战态势的多变性，在诸多影响战斗机空战效能的因素中，几乎每一种因素都难以用确定的量来刻画对空战效能的影响程度，更无法确切描述各影响因素与战斗机空战效能之间的解析关系，这无疑给空战效能的科学评估工作带来了很大困难。为此，研究人员提出了诸多空战效能评估方法，其中比较典型的，诸如粗糙集［1-3］、贝叶斯网络［4］、TOPSIS［5］、神经网络［6-7］和支持向量机（Support Vector Machine，SVM）［8］等。然而，这些评估方法在参数设置、计算复杂性、实现难度、满足精度要求等方面都或多或少存在着不足。本文围绕SVM 的改进版本—最小二乘SVM （Least Square SVM，LSSVM）在空战效能评估中应用展开研究。与标准SVM 相比，LSSVM 具有大致相当的逼近能力以及更快的学习速度［9-10］。然而，在工程实践中，由于系统复杂性以及内部要素交互耦合，使用单纯LSSVM 建模，难以达到理想精度，甚至无法解决问题。在本文的空战效能评估问题中，由于各种因素的影响，可能存在冗余和多重共线性，对LSSVM 建模和评估过程会有负面影响。有必要探索一种围绕提高LSSVM 工程应用效果的组合评估方法，以解决LSSVM 建模前的数据特征提取问题。

基于此，在构建LSSVM 模型过程中，引入一种有监督局部保留投影（Supervised Locality Preserving Projections，SLPP）的特征提取技术，通过将SLPP 与LSSVM 有机结合，优势互补，以实现空战效能的客观评价，并给出了实例验证。

1 空战效能综合评估指标体系构建

空战是利用飞行器在空中进行战斗，以击落对方，夺取制空权为目的的一种战争形式，现代典型空战的基本态势如图1 所示。通常包括搜索、接敌、攻击和退出战斗等阶段。搜索阶段，是指在指挥所引导下，用机载设备或目视，为发现和识别空中目标所作的机动飞行阶段；接敌阶段，是指为获得有利攻击态势而进行的机动飞行阶段；攻击阶段，是指用机载航炮、导弹打击目标阶段；退出战斗阶段，为空战终止阶段。以上各阶段并没有严格界限和区分，并且实际空战影响因素诸多，交互耦合复杂，充满了不确定性。基于此，要构建反映实际的空战效能综合评估指标体系，不仅要详细研究空战过程和战斗机的特点，还要从影响因素分析入手，充分征求专家的意见，根据现有的成果和规范标准，并遵循系统性、科学性和可测性的原则。本文选取文献［1］中的空战效能综合评估指标体系，如下页图2所示。

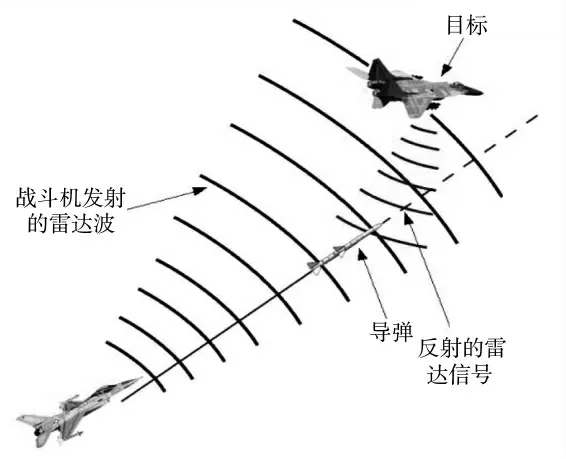
图1 典型空战基本态势图

图2 空战效能综合评估指标体系

式中，Dd表示雷达反射截面为5 m2最大发现目标距离（km），Abearing表示最大搜索方位角（°），Pd为发现目标概率，m1和m2分别为跟踪目标数量和同时允许攻击目标数量。K2代表雷达体制衡量系数，其取值见文献［11］。红外搜索装置的探测能力参数的计算同式（2），区别在于K2取值需要改变［4］。信息系数sa的基本值为0.5，有数据链在此基础上加0.1～0.2，有敌我识别装置加0.10～0.15，有GPS 导航系统加0.1，有无线电通信电台加0.1，但sa最大值不能超过1.0。

其他评估指标也都有各自的量化计算方法，具体过程见文献［11］。

2 SLPP 特征提取

SLPP 是对无监督局部保留投影法（Locality Preserving Projection，LPP）向有监督版本的扩展［12-13］。该方法能够充分利用数据的局部信息和类别信息，使得映射后的同类数据之间的距离尽量变小，而异类数据之间的距离尽量变大。这一性质使得SLPP适用于基于分类的特征提取。

SLPP 的目标函数如下：

式中，a 为投影向量。如果通过上式可求解出d 个投影向量，则也能相应得到d 个特征值。

SLPP 算法的实现步骤：

步骤1 采用k-近邻法构建两个邻接图，分别为类内邻接图和类间邻接图。

1）类内邻接图。当点i 为点j 的k 个类内近邻点，或点j 为点i 的k 个类内近邻点，点i 和点j 用边连接起来。

2）类间邻接图。当点i 为点j 的k 个类间近邻点，或点j 为点i 的k 个类间近邻点，点i 和点j 用边连接起来。

步骤2 赋权，分别通过下式计算W 和B。

3 LSSVM 模型

LSSVM 继承了标准SVM 的结构风险概念和核映射思想，并通过求解变换后的线性方程组来训练SVM，极大提高了SVM 的训练效率［9］，这也是LSSVM 能够迅速推广使用的一个重要原因。

在上式中，C 是经验风险和置信区间的折中系数，也即正则化参数。ξi为非相关随机误差。

以上约束优化问题可由Lagrange 方法转化为以下形式

为保证LSSVM 泛化性能，参数C 和σ2需要采用k-折交叉验证法与网格搜索法进行优化［14］。k-折交叉验证法的处理过程：通过随机方式把训练数据划分成k 个子集，并使各子集中的训练数据个数相等或近似相等。选择k-1 个子集作为LSSVM 训练集；余下一个子集作为验证集。通过训练可得到式（13）的估计模型，将验证集输入向量代入所得到的估计模型中，可计算出验证集输出向量的估计值，如此反复执行k 次，直到k 个子集作为验证集都被不重复执行一次。通过k 次验证集输出向量的真实值与估计值的差，可计算出MSE。网格搜索法的处理过程：在给定C 和σ2的各自取值范围内，分别等距离分出P 个点和Q 个点，构成了一个P×Q的网格，网格上的点即为C 和σ2组合。对网格上各点对应的C 和σ 都执行k-折交叉验证过程，可计算网格上各点的MSE，最小MSE 的网格点对应的C和σ2，即为所求的最优C 和σ2。若无法达到预期，可选取前面优化中较小MSE 对应的C 和σ2，在此基础上执行特征分解，计算特征值和对应的特征向量，并再次界定网格，执行更加精细的优化过程，直到搜索出预期的C 和σ2组合。

4 空战效能SLPP-LSSVM 综合评估模型

由于空中作战的非线性、不确定性、模糊性等特点，造成了影响空战效能的要素之间的耦合交互，并使之呈现较强的非线性特征。虽然前面在构建空战效能综合评估指标体系过程中，遵循了科学的设计原则与构建流程，但仍难以确保各评估指标之间的绝对不相关，不满足LSSVM 建模输入的独立性要求，影响了评估结果的可信性。此外，由于数据的采集处理以及指标选取的主观性等原因，指标数据中难免存在一些噪声成份和信息冗余，这也会对LSSVM 的计算复杂性和模型精度造成影响。因此，为保证评估结果的准确性和客观性，在构建LSSVM 评估模型前，需要预先对指标评估数据进行特征提取，以解决上述存在的问题。

基于以上分析，针对空战效能综合评估问题，本文提出了基于SLPP 特征提取的LSSVM 的模型，其评估流程如图3 所示。该过程大致可分为两部分：首先，采用SLPP 提取指标数据的低维特征；然后利用SLPP 提取的特征，构建LSSVM 模型并完成空战效能评估。在此过程中，SLPP 的特征提取作用，主要体现在降低输入维数、消除指标数据中存在的多重共线性和噪声，以期简化LSSVM 的网络结构，提升评估模型的性能，进而对空战效能作出正确反映。

图3 空战效能SLPP-LSSVM 评估流程

根据上述思想，SLPP-LSSVM 的输入由评估指标数据组成，共9 维。而输出为空战效能评估等级数据（高、较高、一般、较低和低，分别用数字1、2、3、4、5 表示）。

5 算例分析

构建了空战效能综合评估指标体系，即可按照图3 的流程完成建模与评估。下页表1 给出空战效能的专家评估基础数据，数据来源于文献［3，8］。对表中数据进行标准化处理，得到数据样本。选取样本1～63 用于SLPP-LSSVM 模型的训练，样本64～69 用于模型检验。本文所涉及计算，基于LS-SVMlab1.5 工具箱在MATLAB 编程环境中实现。并假设SLPP-LSSVM 的实际输出与期望输出之差的绝对值小于判定值0.2，可认定评估出的等级是正确的；否则，认定评估错误。

表1 三代以上战斗机不同机型及其典型挂载方案下的样本数据

为了解SLPP 特征提取处理效果，并与LPP 和LFLD 对比，将表1 中的1～63 号样本分别用图标来表示，如表2 所示。先将“△”类样本视为一类，而将“○”、“□”、“◇”和“☆”4 类样本视为另外一类。这样即得到一个二分类问题。图4 分别给出LPP、LFLD 和SLPP 特征提取后的二维尺度下的处理效果。从图4 中不难看出，LPP 处理后，“△”类与“○”类存在混淆；LFLD 处理后。“△”类与其他各类存在边缘重叠，类间距离不清晰；而经SLPP 处理，类间距离明显，能将“△”类与其他各类很好区分。总体上SLPP 处理效果最好。

图4 各方法二维特征提取效果

表2 空战效能等级及其图标

为量化呈现上述特征提取效果，分别采用LPP、LFLD 和SLPP 提取评估指标数据的主元特征，并选取前5 个主元作为输入，以表1 中的空战效能的量化值作为输出，优化超参数，训练LSSVM 评估模型，并检验测试。

优化LSSVM 超参数，可将10-折交叉验证法与网格搜索法组合起来，实现对正则化参数C 和核宽度参数σ2的优化搜索。为测试组合方法的稳定性，可分别将C 和σ2设定为不同初始值，10-折交叉验证过程中，训练样本可划分为5 个子集。由于C和σ2不属于同一数量级，且相差较为悬殊，搜索过程可分为两个步骤，即先粗搜索再精搜索。粗搜索的网格点“·”个数为10×10，选取较大步长，通过误差等高线划定最优C 和σ2对应网格点的范围；精搜索的网格点“×”个数同样为10×10，在粗搜索给出的范围内，选取相对较小步长执行精细搜索。图5给出不同C 和σ2初始值下的搜索过程。

图5 不同C 和σ2 初始值下的搜索过程

将以上搜索过程得到的最优C 和σ2组合，用于训练LSSVM 评估模型，并将表1 中64～69 号样本中的指标F1～F9数据标准化后，输入所构建LSSVM 模型，计算出相应的空战效能评估值。表3给出不同初始C 和σ2值下的SLPP-LSSVM 模型的评估值；而表4 对比了LSSVM、LPP- LSSVM、LFLD-LSSVM 与SLPP-LSSVM 的评估结果。

表3 SLPP-LSSVM 模型评估检验结果

由表3 和表4 可看出，LPP-LSSVM、LFLDLSSVM 与SLPP-LSSVM 模型的错判率都低于单纯的LSSVM 模型，说明经LPP、LFLD 和SLPP 预处理的评估效果要优于单一LSSVM。尤其是经SLPP 特征提取构建的LSSVM 模型，在不同初始参数值情况下，得到的评估结果与专家评估结果完全一致，对测试样本没有出现错判，这是由于基于局部结构的SLPP，可提取有辨识力的低维特征，并能有效消除指标数据的多重共线性，以及所含噪声干扰，同时，也降低了LSSVM 输入维数，简化了网络结构，证明了SLPP-LSSVM 在解决空战效能评估问题中的优越性。

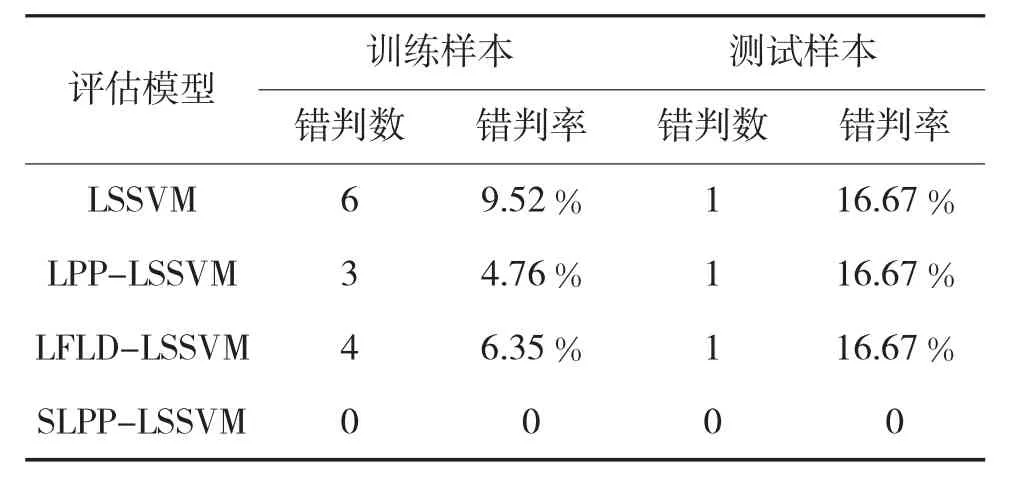
表4 各模型评估等级错误率对比

6 结论

本文在空战效能综合评估指标体系基础上，建立了SLPP-LSSVM 空战效能评估模型。实例计算表明，较之于LSSVM 模型、LPP-LSSVM 模型和LFLDLSSVM 模型，基于SLPP 特征提取的LSSVM 模型，既可以消除冗余和多重共线性，又能够简化模型结构，提高评估精度。因此，采用该模型进行空战效能综合评估是有效可行的。