考虑电子雷管延期误差的隧道爆破叠加振动研究*
2021-12-28刘翔宇吴昊骏吴晓东王思杰
刘翔宇,吴昊骏,吴晓东,王思杰
(北京科技大学 土木与资源工程学院,北京 100083)
普及电子雷管起爆系统是未来工程爆破发展的趋势,电子雷管作为一种新型爆破器材,具有可任意设置起爆时间、起爆精度高等优点,目前已在各类爆破工程中广泛应用[1-5],取得了良好的爆破效果。
在隧道电子雷管爆破中,学者们通过现场试验对比法[6,7]、半周期错相减振法[8,9]、多孔波形叠加法优选了孔间延时[10],显著降低了爆破振动强度。上述研究在应用电子雷管实现降振时,通常不考虑其延期误差。实际上电子雷管起爆时间虽然准确,但仍然存在一定的延期误差[11,12]。城市隧道爆破尤其是复杂环境下的城区隧道爆破中需要严格实现低振速控制时,需要考虑雷管延期误差对多孔延时爆破振动的影响。以往学者们多研究导爆管雷管延期误差对爆破叠加振动的影响,许红涛等通过遗传算法研究了导爆管雷管延期误差引起的爆破振动叠加对的最不利情况[13];韩亮等通过引入概率模型,定量分析了因导爆管雷管的延期误差而引起的干扰降振的概率值[14];吴昊骏等根据实测的各段导爆管雷管延时范围[15],基于Anderson叠加理论获取了8孔延时爆破百万种以上的全部合成振动组合,分析了各段延时误差对振速影响。目前,针对电子雷管延期误差对爆破叠加振动的影响少有研究。
以重庆市观音桥隧道为背景,基于Anderson叠加理论[10,15],考虑各段电子雷管延期误差,设计计算程序并优化算法,解算出4孔微差爆破近万种全部合成振动组合,分析了雷管实际延期误差及延期精度对多孔延时爆破叠加振速的影响。研究结果可为隧道爆破电子雷管的现场应用提供一定的参考依据。
1 工程背景
重庆市观音桥商圈北大道隧道,位于重庆市中心区域,施工区间有密集地面建筑物及地下管线,隧道埋深为20~30 m,要求地面振速不超过1.0 cm/s。在同类型爆破工程中控制指标严苛,施工难度大。
爆破试验在隧道左洞K1+330~K1+367区段进行,隧道断面尺寸为11.8 m×9.55 m,面积90.85 m2,采用电子雷管全断面爆破,电子雷管延期误差为±1 ms。爆破区主要为砂岩,无不良地质现象,隧道围岩类别为Ⅳ级。
2 有无延期误差下四孔叠加最大振速计算
在隧道爆破振动波形中,由掏槽爆破引起的振速往往是振动全过程中的最大值。因此,针对掏槽爆破振动叠加过程中电子雷管延期误差的影响进行研究。由于楔形掏槽是隧道爆破的常用掏槽方式,掏槽孔数根据隧道断面大小及岩石性质等参数确定,以四孔楔形掏槽为例,计算不同孔间延时下四孔叠加最大振速。
首先进行不考虑延期误差时的叠加计算,作为参考,然后进行考虑延期误差时的叠加计算,最后将二者结果进行对比,分析电子雷管延期误差的对爆破振动的影响。
2.1 不考虑延期误差时的四孔叠加最大振速计算
2.1.1 单孔波形的选取及拟合
在隧道左洞工作面掏槽区分别进行1.2 kg、1.4 kg药量的单自由面单孔爆破试验,在工作面地表正上方监测,得到相应振动波形。每种药量均试验3次以上,对比多次试验结果,发现相同条件下同药量波形基本一致。1.2 kg、1.4 kg的典型单孔波形如图1所示,最大振速分别为0.512 cm/s、0.897 cm/s。

图 1 现场实测单自由面单孔振动波形Fig. 1 Single-hole vibration waveform of single free surface measured on site
由于所获波形{[tn,g(tn)]}是离散数据,为便于叠加计算,需要先将波形拟合为连续函数,采用Fourier级数的三角函数形式,参照文献[10]的步骤,利用MATLAB编程计算,得到单自由面单孔波形函数v(t)。
2.1.2 不同孔间延时对应的最大振速计算
隧道爆破中,掏槽孔距相对于各掏槽孔至测点的距离可忽略不计。基于Anderson叠加理论,认为4个掏槽孔取相同的单孔波形函数,且各孔孔间延时取相同值。采用线性叠加方法,在1~50 ms孔间延时范围内,以1 ms为增量,对1.2 kg、1.4 kg药量的单孔波形函数v(t)进行四孔波形叠加,得到各延时下的叠加波形V(t,{Δti}),如式(1)所示。
(1)
式中:V(t,{Δti})为叠加波形;v(t)为单自由面单孔波形函数;Δti为第i个掏槽孔起爆时间;Δt为孔间延时,取值1~50 ms。
取叠加波形V(t,{Δti})中正、负向最大振速绝对值的较大值,得到各延期时间Δt对应的最大叠加振速Vmax(t,{Δti}),1.2 kg、1.4 kg药量下,1~50 ms延时下的四孔叠加最大振速如图2所示。
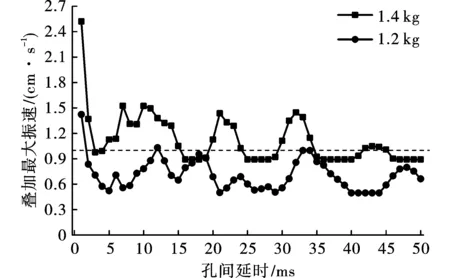
图 2 1.2 kg、1.4 kg药量各延时的叠加最大振速Fig. 2 The maximum superposed vibration velocity under each delay time of 1.2 kg and 1.4 kg charges
由图2可以看出,1.2 kg药量下,1~50 ms延时的叠加最大振速普遍低于安全振速,只有个别孔间延时(1 ms、12 ms)的叠加振速超标,其中叠加最大振速较小(与单孔最大振速相近)的延时有5 ms、21 ms、29 ms、40~44 ms;而1.4 kg药量下,1~50 ms延时范围内,部分延时的叠加最大振速接近安全振速,但尚未超标,包括3~4 ms、16~19 ms、25~29 ms、35~41 ms、46~50 ms,其他部分延时的叠加振速已超标。
2.2 电子雷管延期误差对叠加最大振速的影响研究
2.2.1 延期误差下各延时的叠加最大振速计算
现场所用电子雷管的延期精度为±1 ms,电子雷管的实际起爆时间在其延期误差范围内随机分布。孔间延时以0.1 ms为误差微元,计算电子雷管延期误差的影响,根据式(1)采用枚举法对所有可能的起爆时间组合进行遍历叠加计算,求取叠加最大振速。
当考虑电子雷管延期误差时,各掏槽孔的实际起爆时间在如下范围内
Δti,real∈{(i-1)Δt-err,(i-1)Δt+err}
(2)
式中:Δti,real为第i个掏槽孔的实际起爆时间,i=2,3,4;err为电子雷管延期误差,取值1 ms;Δt为孔间延时,取值1~50 ms。
以5 ms孔间延时为例,第1个掏槽孔的起爆时间为0 ms,第2个掏槽孔的实际起爆时间在4~6 ms范围内,第3个掏槽孔的实际起爆时间在9~11 ms范围内,第4个掏槽孔的实际起爆时间在14~16 ms范围内。
孔间延时以0.1 ms为误差微元,因此第2~4孔每个炮孔的实际起爆时间均有21种可能,则四孔掏槽的起爆时间组合有321(9261)种,对应321种叠加振动波形和321个叠加振速最大值,是否超标难以直接判断。因此,对1~50 ms孔间延时,遍历计算所有可能起爆时间组合的叠加最大振速,得到1.2 kg、1.4 kg药量各延时条件下考虑电子雷管正负最大1 ms延期误差的叠加最大振速,如图3、图4所示。
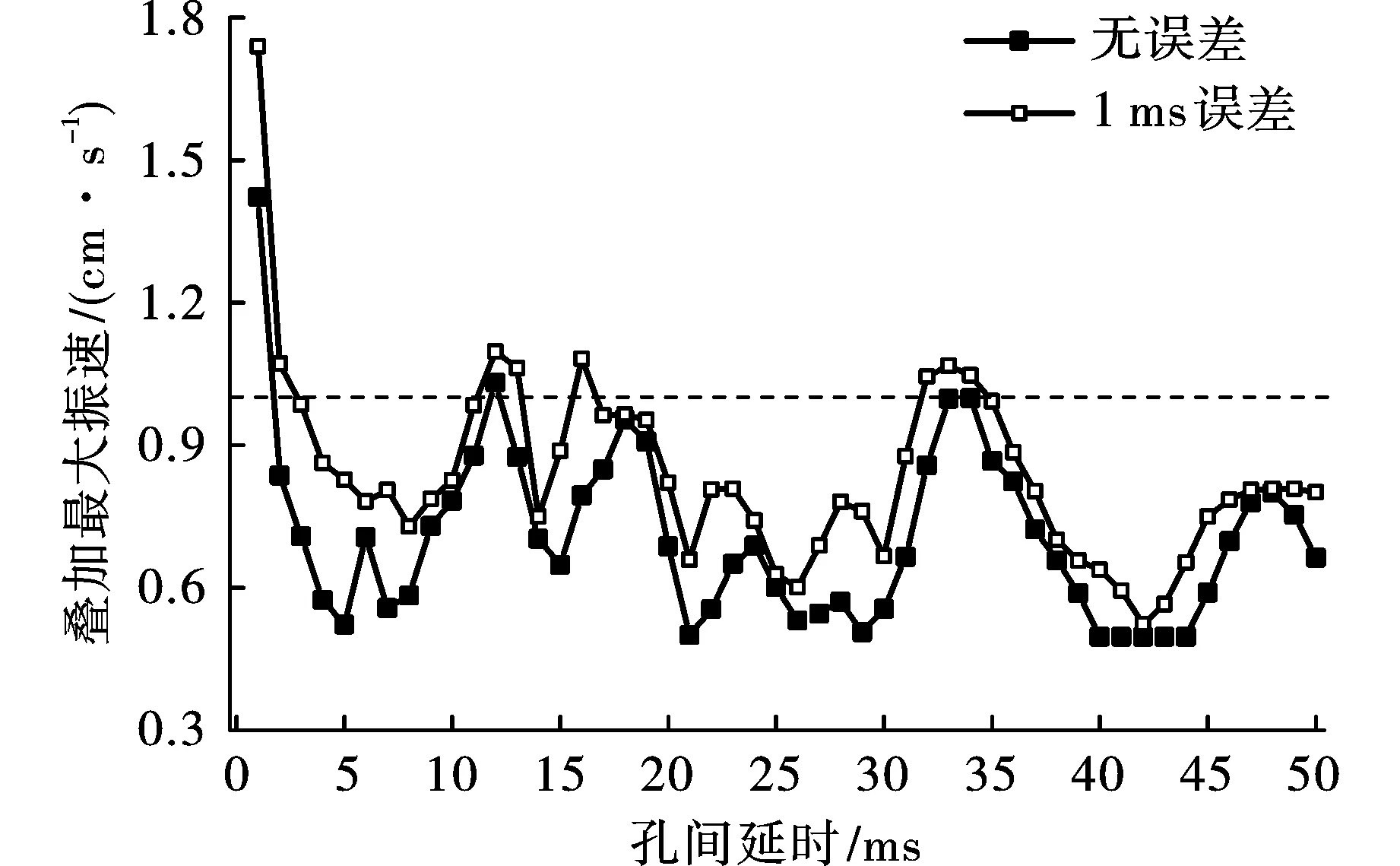
图 3 1.2 kg药量有无延期误差各延时的叠加最大振速Fig. 3 The maximum superposed vibration velocity of each delay time of 1.2 kg charge with or without delay error
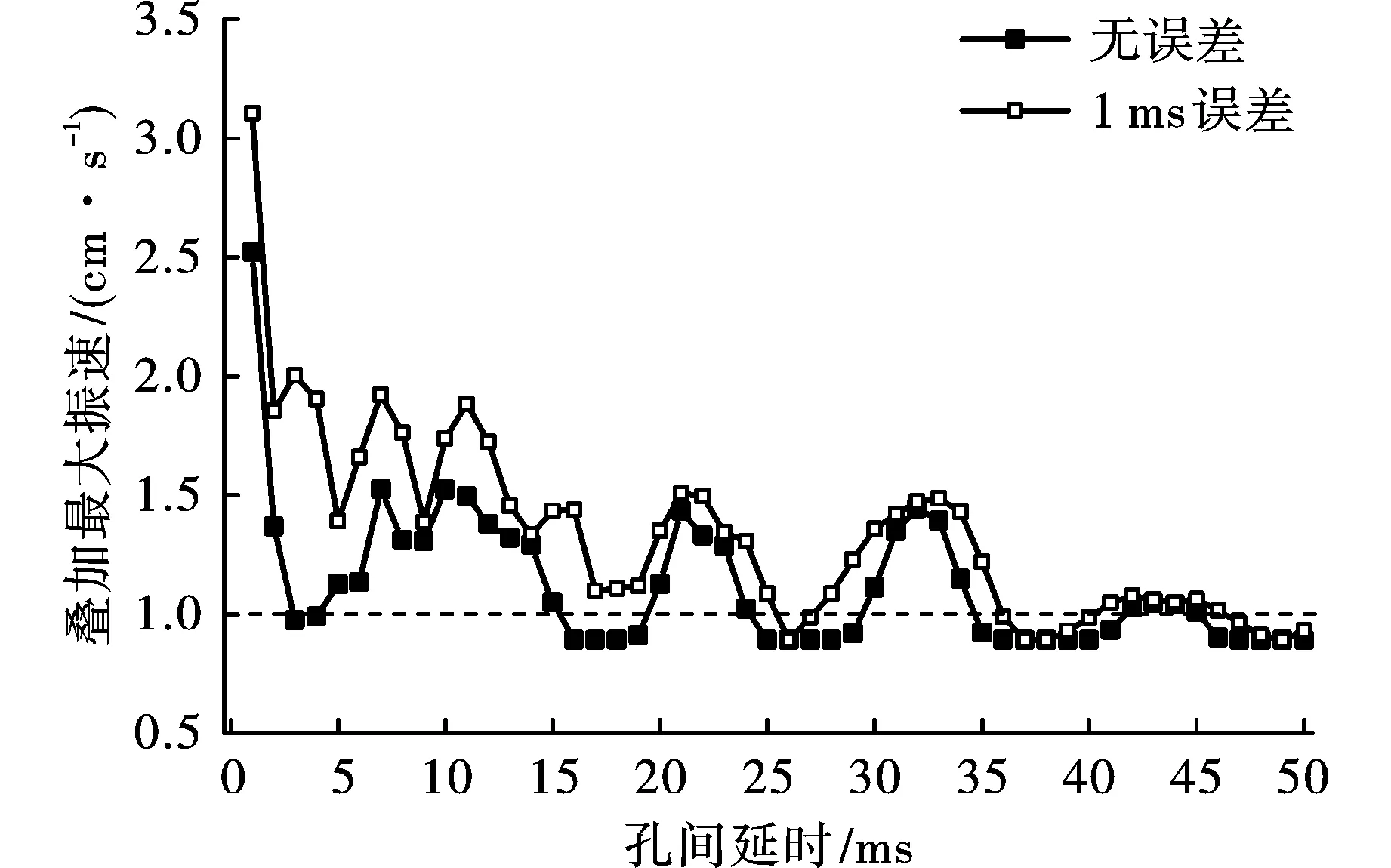
图 4 1.4 kg药量有无延期误差各延时的叠加最大振速Fig. 4 The maximum superposed vibration velocity of each delay time of 1.4 kg charge with or without delay error
由图3、图4可以看出,当考虑电子雷管的延期误差时,1.2 kg、1.4 kg药量下所有延时的叠加最大振速几乎均有不同程度的增加。1.2 kg药量下,大部分延时的叠加振速仍远离安全振速,但也有个别延时的叠加振速超标;1.4 kg药量下,大部分延时的叠加振速超标,只有26~27 ms、36~40 ms、47~50 ms延时的叠加振速未超标,相比于不考虑延期误差的情况,振速超标的孔间延时数量明显增多。
2.2.2 不同孔间延时下延期误差对叠加最大振速的影响研究
为了对比不同孔间延时下延期误差对叠加最大振速的影响,求有无延期误差下各孔间延时的叠加最大振速差值,如图5所示。

图 5 1.2 kg、1.4 kg药量考虑延期误差时振速差值对比图Fig. 5 Comparison of vibration velocity difference between 1.2 kg and 1.4 kg charge considering delay error
图5中,横坐标是孔间延时,纵坐标是电子雷管精确起爆和考虑±1 ms延期误差的叠加最大振速的差值。由图5可以看出,不同延时的叠加振速差值受延期误差的影响不同,叠加最大振速差值的总体变化趋势为振速差值随孔间延时增大而减小,在局部范围内则随延时变化无规律地上下振荡。两种药量的振速最大差值均出现在较小的孔间延时处,1.2 kg药量在1 ms孔间延时处振速差值最大(0.32 cm/s),1.4 kg药量在3 ms孔间延时处振速差值最大(1.03 cm/s)。这是因为单孔波形振速随时间衰减,较小的孔间延时意味着各掏槽孔在各自波形振速仍较大时就开始叠加,此处振速的变化率也更大,因此导致短延时的延期误差产生更大的叠加振速差值。值得注意的是,受偶然因素影响,有部分短延时的振速差值可能较小,某一延时的振速差值需要经过计算后才能确定。
1.2 kg药量的振速差值变化较为平缓,而1.4 kg药量的振速差值随延时增大而变化较大,尤其是1~16 ms延时范围内的振速差值明显高于17~50 ms延时。这是由于1.4 kg药量的单孔波形峰值振速随时间变化较大,而1.2 kg药量的单孔波形峰值振速随时间变化较小,导致了电子雷管延期误差对两者的影响不同。
此外,对比1.2 kg和1.4 kg药量的叠加最大振速差值发现,在1~16 ms延时范围内,1.4 kg药量的振速差值显著大于1.2 kg药量,如图5灰色阴影标记处所示;在17~50 ms延时范围内,两种药量的振速差值相近。这是由于在20 ms之前,1.4 kg药量的单孔波形振速远大于1.2 kg药量,这也表明了当波形振速较大时,因延期误差产生的振速偏差也较大。
2.2.3 延期误差下振速超标的概率分析
通过上述计算,发现有部分延时在考虑正负最大1 ms延期误差时的叠加最大振速超标,影响现场的安全施工。为此,有必要计算分析上述延时叠加振速超标的概率,采取妥善的限制措施。计算公式如下
p=sun[Vmax(t,{Δti,real})>1.0]/N×100
(3)
式中:sum(Vmax(t,{Δti,real})>1.0)为超过安全振速的起爆时间组合数量;Vmax(t,{Δti,real})为某实际起爆时间组合下的叠加最大振速;Δti,real为第i个掏槽孔的实际起爆时间;N为所有可能的起爆时间组合总数量,为321(9261)种。
考虑到1.2 kg药量下大部分延时的叠加振速均小于安全振速,因此选择1.4 kg药量,根据式(3)计算并分析1~50 ms各延时叠加振速超标的概率。计算结果如图6所示。

图 6 1.4 kg药量下各延时叠加振速超标的概率Fig. 6 The probability that the superposed vibration velocity corresponding to each delay time exceeds the safe value under 1.4 kg charge
根据振速超标概率,可将1~50 ms延时分为三类:
第一类,不考虑延期误差时振速已超标;
第二类,无论是否考虑延期误差,振速均不超标;
第三类,不考虑延期误差时振速未超标,考虑电子雷管延期误差时,振速可能超标。
在第三类情况中,3~4 ms、16 ms、19 ms、29 ms、35 ms、41 ms孔间延时的叠加振速超标概率较大(多数在50%以上),而17~18 ms、25 ms、28 ms、46 ms孔间延时的叠加振速超标概率较小(小于5%)。
3 电子雷管延期精度对叠加最大振速的影响分析
随着国内外爆破器材的发展,电子雷管的延期精度将越来越高,本节研究不同延期精度对叠加振速的影响。延期精度是雷管延期误差的最大值,不同厂家生产的电子雷管延期精度存在差异[12],例如I-kon电子雷管(0~100 ms)的延期精度为±0.1 ms,隆芯1号电子雷管(0~100 ms)的延期精度为0.5 ms。
为了量化分析延期精度对振动叠加结果的影响,在计算时延期精依次取值0.1 ms,0.2 ms,…,0.9 ms,1 ms,归纳总结1.2 kg、1.4 kg药量下不同延期精度对各延时四孔叠加振速的影响。
在1~50 ms延时范围内选取典型的延时进行分析。由上述计算结果可知,1.4 kg药量下,存在少数延时,延期误差正负最大1 ms对叠加最大振速无影响,因此在研究延期精度的影响时不能选择这些延时。分别在1.2 kg和1.4 kg药量的各延时中选取叠加振速较小同时受延期误差影响的延时进行分析,1.2 kg药量下孔间延时选取5 ms、22 ms、28 ms、45 ms,1.4 kg药量下孔间延时选取3 ms、19 ms、29 ms、35 ms、46 ms。
根据式(1)、(2)计算1.2 kg、1.4 kg药量在上述孔间延时下不同延期精度的叠加最大振速Vmax(t,{Δti}),计算结果如图7、图8所示。
由图7、图8可以看出,叠加最大振速随延期精度变化近似符合线性增大的规律。其中,1.2 kg药量下,不同延期精度对长短延时的叠加最大振速的影响相近;而1.4 kg药量下,延期精度对短延时3 ms叠加最大振速的影响明显大于其他延时,这是由于3 ms延时的波形叠加条件下,各单孔波形的振速仍处于高位,尚未出现明显衰减,且振速的变化率更大,导致延期精度对叠加振速的影响更大。
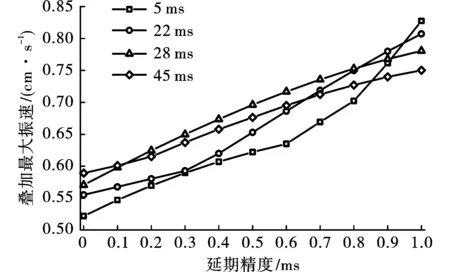
图 7 1.2 kg药量不同延期精度下的叠加最大振速Fig. 7 The maximum superposed vibration velocity of 1.2 kg charge under different delay accuracy
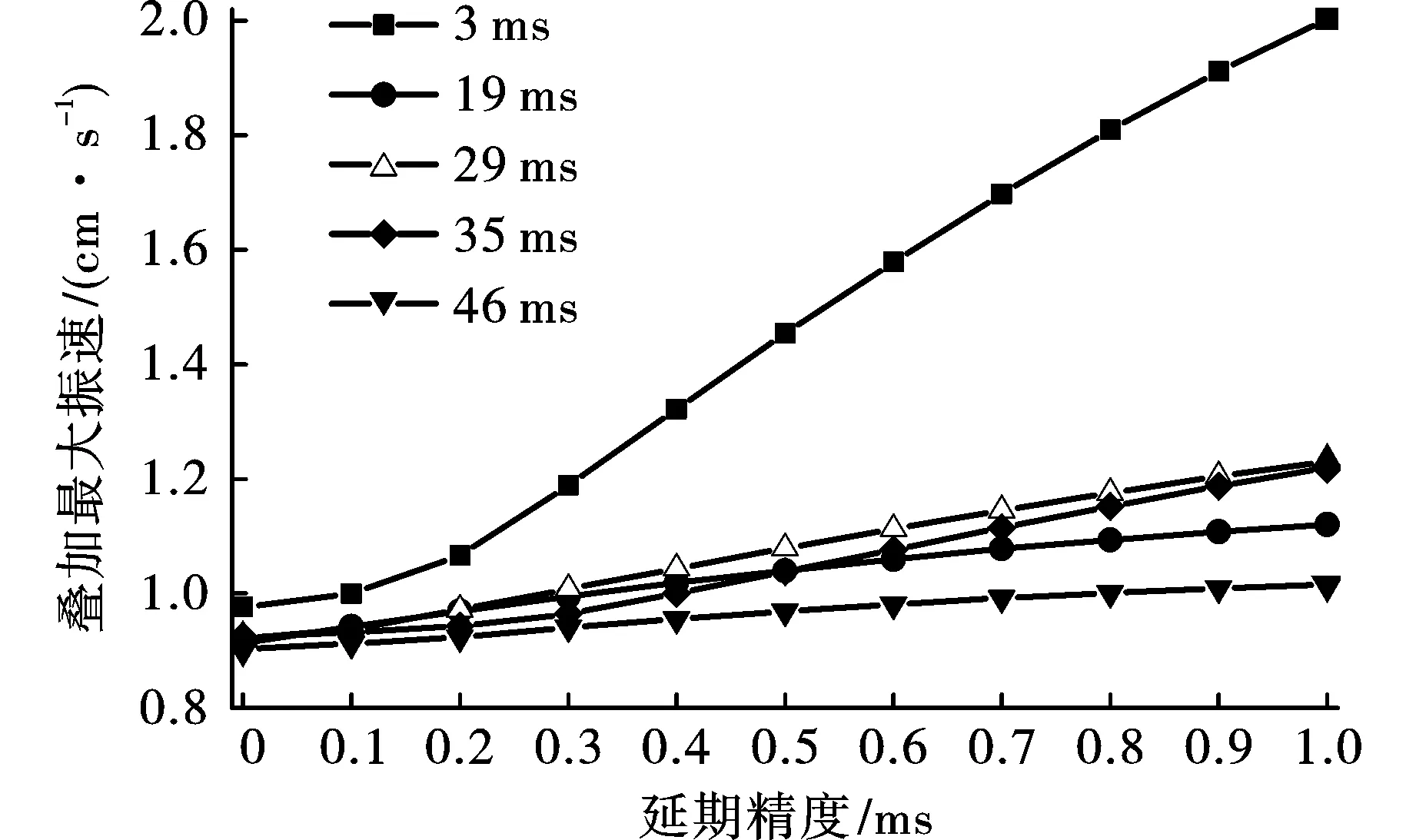
图 8 1.4 kg药量不同延期精度下的叠加最大振速Fig. 8 The maximum superposed vibration velocity of 1.4 kg charge under different delay accuracy
4 结论
(1)在考虑电子雷管延期误差时,各延时的叠加最大振速几乎均有不同程度的增加;电子雷管的延期误差对较大药量的叠加振速影响更大,有无延期误差下,1.4 kg药量的叠加振速最大差值是1.2 kg药量的3倍。
(2)根据叠加振速是否超标,可将孔间延时分为三类:第一类,无延期误差时,叠加振速已超标;第二类,有无延期误差,叠加振速均不超标;第三类,考虑电子雷管延期误差时,叠加振速存在一定概率超标。当爆破振速要求严苛时,应选择有无延期误差振速均不超标的孔间延时。
(3)电子雷管延期误差对叠加振动的影响整体上随延时增大而减小,在局部范围内有无延期误差的振速差值随延时无规律地变化。
(4)叠加最大振速随延期精度的变化大致符合线性增长的规律。因此,有必要进一步提高电子雷管的延期精度,以降低延期误差对多孔爆破叠加振动的影响。
