深埋式桩板结构桥-隧过渡段动力响应特征分析
2021-12-28李双龙魏丽敏何重阳
李双龙 ,魏丽敏 ,2,何 群 ,2,何重阳
(1. 中南大学土木工程学院,湖南 长沙 410075;2. 中南大学高速铁路建造技术国家工程实验室,湖南 长沙410075;3. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
桩板结构路基通过轨道结构下铺设的承载板与群桩基础能够将上部荷载传递至深部地基,从而达到降低路基永久沉降的目的[1-2]. 按照承载板的埋置深度进行分类,桩板结构路基可分为非埋式、浅埋式及深埋式[3]:承载板与轨道结构直接连接为非埋式;承载板上部通过基床表层与轨道结构相连为浅埋式;桩板结构埋置在路堤基底(承载板上部为填方路基)为深埋式. 詹永祥等[4]开展了非埋式桩板结构路基模型试验,试验表明桩基的存在加深了路基动力影响范围;苏谦等[5]对郑西线某非埋式桩板结构路基的应力与沉降变形进行观测,数据表明测点最大累计沉降仅为1.0 mm;还有其他学者[6-7]建立有限元模型对非埋式桩板结构路基的动力特性进行研究,获得了路基动力响应(动应力、动加速度等)的空间分布;苏谦等[8]考虑浅埋式桩板结构温度效应,建立了温度作用下桩板结构温度力的计算模型.
以上研究主要集中在非埋式与浅埋式桩板结构路基,而有关深埋式桩板结构路基方面的研究相对较少,特别是当深埋式桩板结构路基用作过渡段时,相关报道更是少见. 上海-昆明高速铁路江西段某工点针对桥梁与隧道之间因距离短而无法设置常规过渡段(如倒梯形过渡段)[9]的情况,首次将深埋式桩板结构路基用作该工点桥梁-隧道过渡段[10],作为一种新型过渡段,其过渡效果及动力特性值得进一步研究.
为此,本文针对该工点桥-隧过渡区(包含隧道口、过渡段及桥台)展开现场动力响应测试,研究过渡区在列车激励下的动力响应分布规律,并且建立考虑车辆-轨道-路基耦合振动数值模型,研究桩板结构过渡段的竖向动应力分布及过渡区列车行车平稳性,进而对过渡区线路平顺性作出评价.
1 现场试验
1.1 过渡段结构组成
所研究过渡区总长约39.2 m,过渡段长度约26.0 m,两端分别与隧道及桥梁相连,见图1(a),图中:B0、S1、S2、S3 和T0 为横向测试断面. 过渡区地表土层为第四系全新统残坡积(Q4el+dl)粉质黏土,最大厚度约为20.0 m,下伏二叠系下统茅口组(P1m)灰岩.
过渡段基床表层厚度0.4 m,为级配碎石填料;基床底层厚度2.3 m,为级配碎石混合5%水泥填料;基床底层以下为两联桩板结构,由承载板和钻孔灌注桩组成,见图1(b). 承载板为钢筋混凝土结构,钻孔灌注桩与承载板刚性连接,靠近隧道一联采用等桩长设计,靠近桥台一联采用不等桩长设计,结构尺寸见图2.
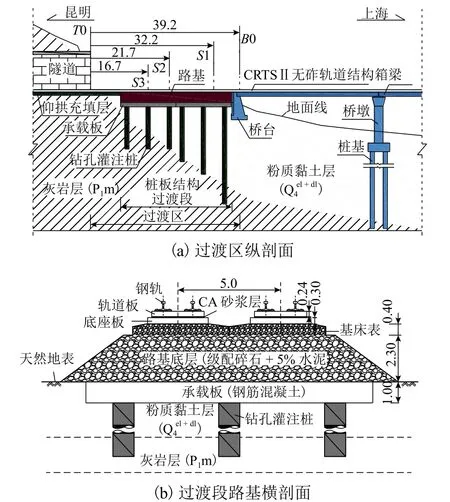
图1 桥-隧过渡区结构概况(单位:m)Fig. 1 Schematic profile of the transition zone (unit: m)

图2 桩板结构尺寸(单位:m)Fig. 2 Pile-plank structure (unit: m)
1.2 监测布置及数据采集
过渡区共设置5 个横向测试断面(B0、S1、S2、S3 和T0),里程DK722+522.8~DK722+562.0. 每个断面测点的位置分布在上行线和下行线底座板的内外两侧、线路中心线路基表面以及路基两侧边坡位置,见图3,T0-2:T0 代表监测断面,2 代表测点编号,其余同理. 测试列车包含CRH380B、CRH2、CRH380A-001、 CRH380A-6158、 CRH380AM 及DF11共6 种车型,对应列车轴重分别为16、13、14、14、15、22 t. 建立了行车自动触发的数据采集及无线传输测试系统,采用891-Ⅱ型拾振器监测振动信号,891-Ⅱ型拾振器包含加速度和速度两种档位,加速度档位最大量程为40 m/s2,灵敏度为0.1 V•s2/m;速度档最大量程0.5 m/s,灵敏度为30.0 V•s/m. 利用INV3060D 型采集仪对振动信号进行采集,采样频率为256 Hz. 采用DASP(V10)软件对振动速度信号进行全程一次积分可获取动位移.
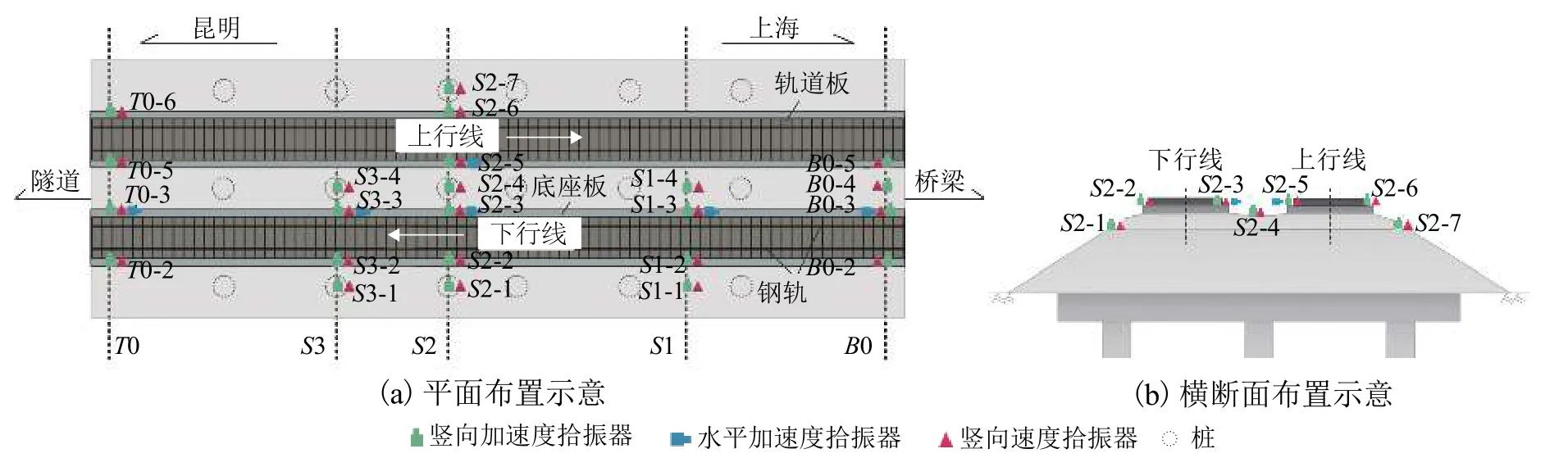
图3 监测布置Fig. 3 Layout of monitoring instruments
2 试验结果与分析
2.1 信号数据处理
采用阻断频率为120 Hz 的低通滤波和频带为49~51 Hz 的带阻滤波对振动信号进行过滤[11]. 提取滤波后振动有效值进行分析,振动有效值采用式(1)计算[12].
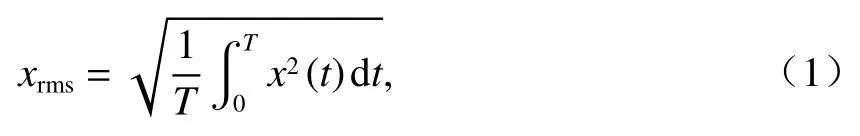
式中:xrms为振动信号有效值;T为振动周期;x(t)为振动信号瞬时值;t为时间.
为了减小试验人为或系统误差,采用区间估计法统计振动信号有效值的置信区间,置信水平为95%. 然后提取上限值作为数据样本分析不同因素对过渡区动力响应的影响.
2.2 车型对过渡区动力响应的影响
图4 分别给出了不同车型列车在下行线行车工况下底座板测点T0-3、S3-3、S2-3、S1-3 及B0-3 振动加速度和动位移有效值的纵向与横向分布.
由图4 可知:相比其他车型,CRH380A-001 型列车引起过渡区的振动加速度有效值整体上更大,这是因为CRH380A-001 列车平均行车速度相比其他车型更大,所引发的路基动力放大效应更明显. 从纵向分布来看,断面T0 及S1 的振动加速度要比断面S2、S3 及B0 的更大. 已有研究表明[13],列车经过轨道刚度突变区域会引发附加动力荷载,使列车及轨道路基振动更加剧烈. 由此推断,列车下行线行车经过桥台至过渡段的连接区域时,列车在该区域产生了附加动力荷载,进而引发断面S1 的振动加强.


图4 不同车型振动加速度和动位移有效值对比Fig. 4 Comparison of effective values of acceleration and displacement under different train types
DF11 车型引起的动位移有效值比其他车型更大,原因在于该车型相比其他车型轴重更大. 在横向上,两侧底座板测点离列车荷载作用位置最近,因而其动位移都要比路基中心及两侧边坡测点的更大.
从以上试验结果来看,不同车型由于轴距、轴重及编组形式等不同,引起过渡区振动响应也不同,但竖向振动加速度及动位移有效值都很小,振动加速度及动位移有效值的最大值分别为0.85 m/s2、0.034 mm,表明在不同车型列车激励下深埋式桩板结构过渡区振动水平较低.
2.3 车速对过渡区动力响应的影响
CRH380A-001 型列车以12 种车速在上行线行车. 图5 分别给出了上行线底座板测点T0-5、S2-5 及B0-5 的竖向加速度和竖向位移有效值随车速的变化情况.
从图5 中可以看出:随着行车速度的增大,隧道、过渡段及桥台测点的振动加速度及动位移有效值也增大,表明过渡区振动水平与车速大小密切相关;由于过渡段填料相比隧道与桥台来说,具有低刚度、高阻尼的特性,使得过渡段的振动响应与隧道或桥台存在明显差异,而车速的增大使得这种差异加剧,进而在纵向上过渡区的振动响应呈现如图5 中的“V”字形分布.

图5 不同车速列车激励振动响应对比Fig. 5 Comparison of dynamic responses under different train speeds.
2.4 行车方向对过渡区动力响应的影响
已有研究表明[14],不同行车方向的过渡段动力响应存在明显差别. 测试过程中,CRH380A-001 型列车在下行线分别以桥至隧、隧至桥两个方向行车.图6 给出了两个方向行车条件下下行线底座板测点T0-3、S3-3、S2-3、S1-3 及B0-3 的振动响应对比.
由图6 可知:在两个行车方向上测点S3-3 及S2-3 的竖向加速度有效值相差不大,但测点S1-3 和B0-3 相差较大. 当方向为桥至隧时,列车由高刚度桥台驶向低刚度过渡段过程中,引起列车对轨道及路基结构的冲击荷载,造成低刚度区域(如断面S1)振动加强;当方向为隧至桥时,由低刚度过渡段驶向高刚度桥台,在桥台附近(如断面B0)会造成振动加强. 两个方向上各个测点的竖向动位移有效值相差不大,主要原因为试验车辆轴重一定,故而行车方向对竖向动位移的影响不大.

图6 不同行车方向动力响应对比Fig. 6 Comparison of dynamic responses in two driving directions
2.5 竖向加速度变化率评价模型
振动加速度是轨道路基动力响应的重要控制指标. 本文尝试采用竖向加速度在过渡区单位长度上的变化率η来反映过渡区振动响应沿纵向分布的变化幅度,如式(2).

式中:Δa为相邻测试断面间竖向加速度差值;Δl为断面间距离.
采用竖向加速度置信水平为95%的置信区间上限值进行分析. 以下行线行车轨道板内侧测点(即测点T0-3、S3-3、S2-3、S1-3 及B0-3)振动响应数据为样本,图7 分别给出了相邻测试断面间的竖向加速度(a1、a2、a3、a4、a5)差值及其变化率范围.
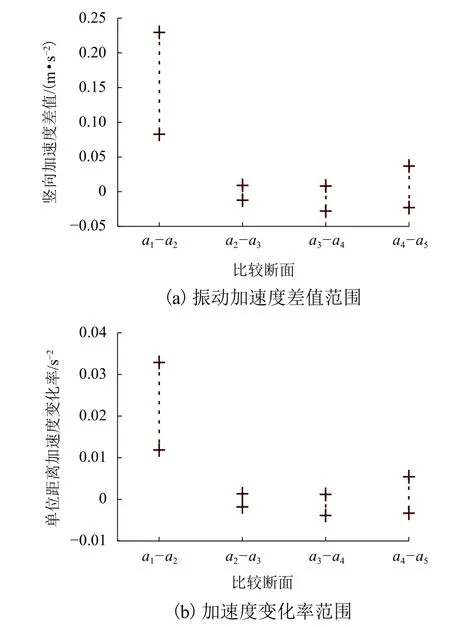
图7 相邻测试断面间的加速度变化Fig. 7 Acceleration changes between adjacent test sections
从图7 中可以看出:过渡段断面S3 至S2、S2 至S1 间的竖向加速度差值及其变化率较接近,并且都很小,表明过渡段内动力响应的分布较为均匀. 对比a1-a2与a4-a5可知,断面T0 至S3 的竖向加速度差值及其变化率显著大于断面S1 至B0,表明桥台至过渡段的平顺性要优于过渡段至隧道的平顺性.
3 数值分析
3.1 数值模型建立
为了更全面地揭示深埋式桩板结构过渡段的动力行为,采用ABAQUS 软件建立考虑车辆-轨道-路基耦合作用的三维有限元模型进行分析. 整体模型由隧道段、过渡段、桥梁段组成,采用C3D8R 实体单元对轨道结构、路堤及地基进行网格划分. LI 等[15]认为为了尽可能消除边界效应,模型纵向边界与轮对作用点距离应大于18 倍的轨枕间距,本计算模型在满足该要求的前提下,同时考虑工作站性能,计算模型在x方向取42.0 m,y方向取80.0 m,z方向取31.5 m,各结构尺寸见图1(b)和图8(a). 桩板结构采用实体单元模拟(图8(b)),其与土层的所有界面设置面-面接触. 桥台与过渡段连接处的动力响应是重点关注部位,因而建立了桥台和简化的单跨简支梁模型,简支梁纵向长度32.7 m,桥面板宽度13.6 m.

图8 数值模型建立(单位:m)Fig. 8 Establishment of numerical model (unit:m)
采用线性弹簧-阻尼单元沿纵向按间距0.65 m(扣件纵向间距)连接钢轨与轨道板来模拟扣件系统.应用赫兹非线性接触理论描述轮轨法向行为,以轮对环形踏面为主面,钢轨轨面为纵面建立接触,采用“罚”函数考虑轮轨切向行为,摩擦系数取0.2. 计算模型不考虑轨道几何不规则性,将轨道考虑为理想化的水平轨道. 以CRH380AM 型号列车的2 节车厢进行模拟计算以考虑相邻转向架引起的动力响应叠加效应,行车速度300 km/h,车厢结构尺寸见图8(c).列车模型由车体、转向架和轮对结构组成,设置为刚体. 本文重点关注轮轨-路基垂向的动力响应,忽略车体的横向作用,采用简化车轨耦合作用模型[16]. 应用赋予线性弹性-阻尼属性的连接单元来模拟列车的二系悬挂系统,相关车辆参数见表1.

表1 车辆参数与扣件参数Tab. 1 Vehicle parameters and fastener parameters
模型四周边界设置黏弹性人工边界单元以防止动应力波在边界处的反射,设置阻尼比为1.0[17],地基土层及路基层采用基于摩尔库伦屈服准则的弹塑性本构模型,其他结构层或土层均采用线弹性本构模型,计算材料参数见表2,部分参数参考文献[18-19]进行取值. 设置最大计算时步为2.5 ms,采用动力隐式积分法进行计算.
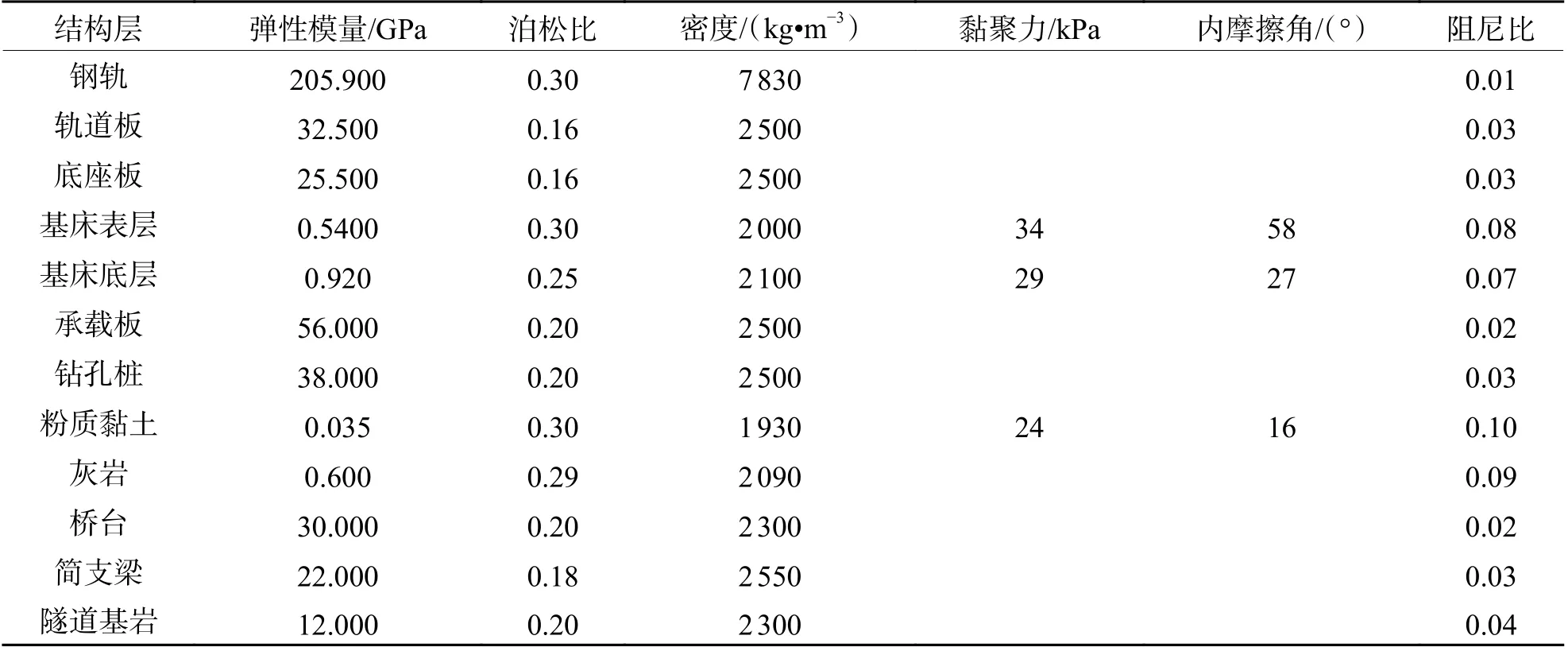
表2 过渡区各结构层材料属性Tab. 2 Material properties of components in the transition zone
3.2 模型验证
图9 为测点S2-3 的振动响应曲线对比. 表3 给出了底座板内侧测点与路基中心测点振动加速度与速度实测值与模拟值的对比. 综合图9 和表3 可以看出,数值模拟得到的振动峰值时间点与实测结果基本对应,并且大部分测点振动响应峰值的计算值与实测值比较接近,相对误差基本小于30%. 不过,仍然有部分测点差别较大,如:T0 断面底座板测点的加速度计算值与实测值相差45.6%,振动速度相差34.5%. 分析认为:隧道口测试断面实测值可能受行车过程空气动力影响较大,而数值分析过程中不能体现这种作用,导致二者出现偏差. 整体上,模拟结果的幅值和分布与现场监测数据较接近,说明数值分析模型的建模方法和计算参数合理可靠.
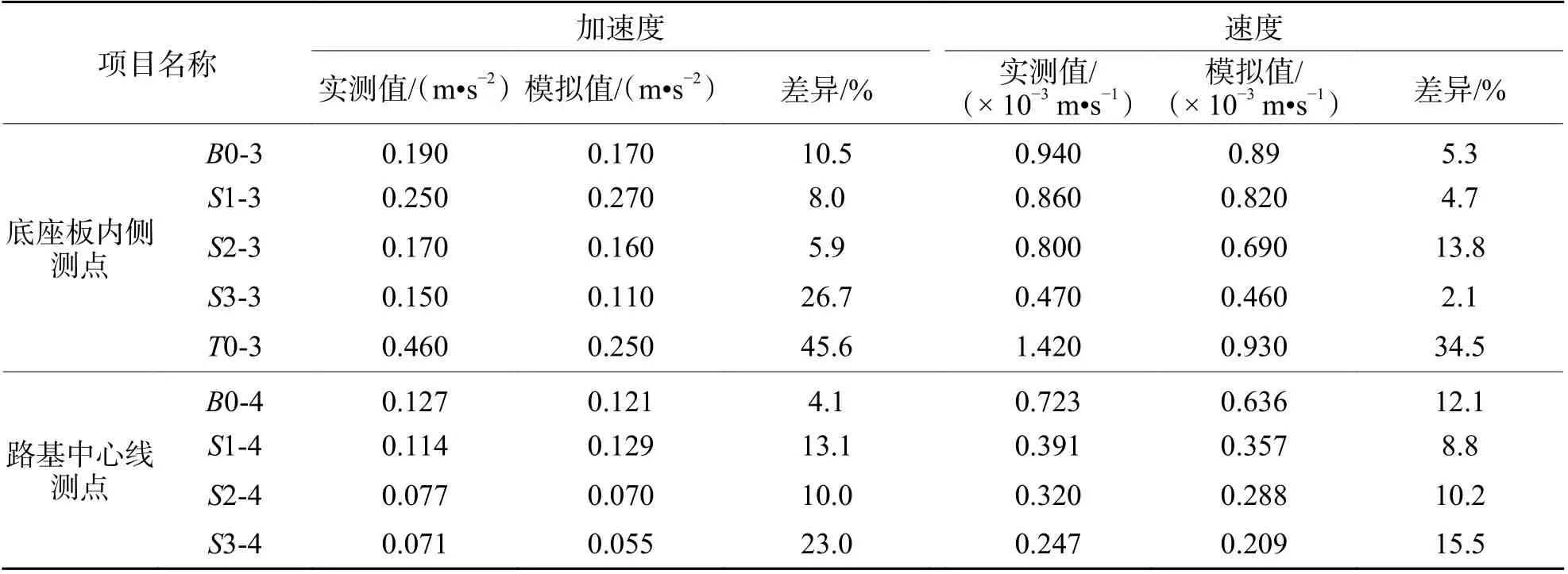
表3 模拟值与实测值对比Tab. 3 Comparison between the numerical results and the field measurements
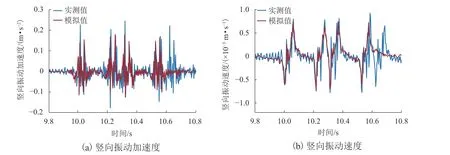
图9 模拟值与实测值对比(测点S2-3)Fig. 9 Comparison between the numerical results and the field measurements (Point S2-3)
3.3 过渡段基床及地基动应力分布
采用验证后的数值模型对过渡段基床及地基动应力分布进行分析,结果如图10.
由图10 可知:列车由桥台驶向隧道过程中,邻近双转向架引起测点的动应力比单转向架的值要大,并且钢轨正下方测点动应力值要比轨道中心线测点动应力值大约17.7%;结合图10(b)可知:行车荷载在路基表面引起的竖向动应力主要分布在转向架的正下方,大致呈“矩形”,并向轨道中心及路基两侧衰减;当轮对位于断面S1 时,最大竖向动应力达到31.23 kPa,而位于断面S3 时为29.14 kPa,由此可以推断,列车由桥台驶向过渡段时,列车对桥台与过渡段连接处及其附近区域的轨道施加了附加荷载,造成断面S1 动应力相比其他断面要大,这也可能是下行线实测值中断面S1 振动水平相比过渡段其他断面要大的原因.

图10 基床竖向动应力分布Fig. 10 Vertical dynamic stress distribution of the subgrade
为了揭示深埋式桩板结构路基及地基的荷载传递规律,图11 给出了断面S3 钢轨正下方基床及地基土体的动应力沿深度分布规律.
从图11 中可以看出:基床层动应力随深度的增大而逐渐衰减,由基床表层顶面29.14 kPa 衰减至基床底层底面6.22 kPa;由于桩板结构的存在,列车荷载主要由桩体承担,造成承载板以下的桩间土体应力很小,仅有1.93 kPa,相应动应力衰减系数仅为0.07,对比一般桩筏加固路基,相同地基深度下动应力衰减系数一般为0.10~0.20[20-21],可见桩板结构的存在能够使浅部地基土体承受的动力作用降低,这也证实了詹永祥等[4-5]的研究结论;在桩端附近,上部荷载通过桩身扩散至桩端底部附近土体,进而引起深部土体应力增大.

图11 基床及地基竖向动应力沿深度分布Fig. 11 Distribution of vertical dynamic stress along the depth of subgrade and foundation
3.4 过渡区线路平顺性分析与评价
为了进一步揭示过渡区轨道等效刚度分布情况,采用式(3)[22]计算竖向轨道等效刚度.

式中:K为竖向轨道等效刚度;Q为列车单轮荷载,本文取值为75 kN;Z为钢轨竖向振动位移幅值.
图12 绘制了钢轨竖向振动位移幅值、轨道等效刚度分布曲线. 由图可知:最大刚度在桥台位置,为94.7 kN/mm,最小刚度在靠近过渡段路基中心的位置,为75.6 kN/mm. 陈小平等[23]认为我国无砟轨道整体刚度在60.0~85.0 kN/mm,该过渡段路基刚度与其结论基本符合. 蔡成标等[24]认为要保证过渡区轨道具有良好的动力学性能,η(钢轨动挠度曲线的斜率)应控制在0.300 mm/m 以内. 由图可以计算出过渡区最大钢轨挠度变化率约为0.149 mm/m. 可见,采用深埋式桩板结构过渡段能够实现桥台-隧道刚度的平顺过渡.

图12 过渡区钢轨位移和等效刚度分布Fig. 12 Distribution of the rail displacement and equivalent stiffness in the transition zone
图13 分别给出了列车在过渡区行车过程中车体、转向架和轮轴的竖向振动加速度响应. 由图可知:当列车以速度300 km/h 从桥台驶向隧道时,由于轮-轨的动态接触作用,轮轴振动竖向加速度变化相比转向架和车体来说更加剧烈;受车体内部悬挂系统的减震作用,转向架及车体振动频率大幅降低,量值也大幅减小;由于过渡段与桥台(或者隧道)的连接处存在刚度差异,轮轴、转向架及车体竖向加速度在该区域出现加速度增大现象,其中过渡段与隧道连接处轮轴加速度最大,为11.77 m/s2,车体最大值0.74 m/s2. 《铁道机车动力学性能试验鉴定方法及评定标准》[25]规定具有优良等级舒适度的车体最大竖向加速度不应大于2.45 m/s2. 从模拟结果来看,以300 km/h 车速经过该过渡区时列车舒适度达到了优良等级,表明过渡区线路平顺性良好.
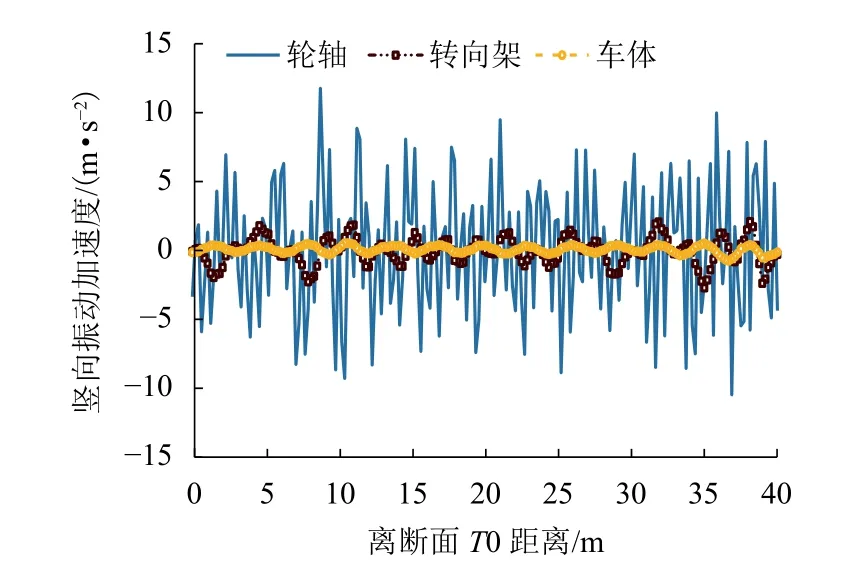
图13 列车经过过渡区时的竖向加速度分布Fig. 13 Vertical acceleration distribution of the train passing through the transition zone
4 结 论
1) 不同车型列车激励下深埋式桩板结构过渡区振动水平较低,过渡区振动加速度及动位移有效值的最大值分别为0.85 m/s2、0.034 mm. 受列车动力附加荷载作用,过渡段与桥台连接区域振动水平比过渡段内其他位置振动水平更高.
2) 过渡区动力响应有效值随车速的增大而增大,过渡段动力响应的增大幅度要比隧道与桥台的更小. 行车方向对过渡段与桥台连接区域的动力响应影响较大,对其他断面影响微弱.
3) 由过渡区相邻断面加速度差值及其变化率可知,深埋式桩板结构过渡段动力响应沿线路纵向分布较为均匀,并且桥台至过渡段的平顺性要优于过渡段至隧道的平顺性.
4) 桩板结构的存在使列车荷载能够传递至深部地基,降低了基床或浅部地基土体承受的动力作用.
5) 列车以300 km/h 车速经过该过渡区时,过渡区内钢轨挠度最大变化率小于控制值,乘客舒适度达到优良等级,表明深埋式桩板结构路基用作该桥台-隧道过渡段时过渡效果良好.
