基于跟驰特性的智能网联车混合交通流轨迹重构
2021-12-28蒋阳升王思琛姚志洪
蒋阳升 ,刘 梦 ,王思琛 ,高 宽 ,姚志洪
(1. 西南交通大学交通运输与物流学院,四川 成都 611756;2. 西南交通大学综合交通大数据应用技术国家工程实验室,四川 成都 611756)
随着无人驾驶技术的发展,未来道路上的智能网联车(connected automated vehicle,CAV)将逐渐普及. 但最新研究表明[1],预计2045 年道路上L4 级别的CAV 渗透率仅能达到24.8%. 因此,未来很长一段时间内,道路上将普遍呈现由常规车(regular vehicle,RV)、网联人工驾驶车(connected vehicle,CV)和CAV 组成的混合交通流. 网联车(CV 和CAV)能够提供海量的车辆轨迹数据,而这些数据蕴含了丰富的时空交通信息,是交通状态估计的基础数据之一. 但由于RV 无法提供自身的轨迹数据,在智能网联环境下全样本车辆轨迹数据仍难以获得. 因此,如何利用已有的轨迹数据来重构所有车辆的轨迹具有重要的意义[2].
近年来,有许多学者对车辆轨迹重构问题进行了探讨,主要为基于经典交通流理论和基于统计概率模型的方法. 这些方法按轨迹重构数据来源可分为三大类:定点检测器、移动检测器和多源数据.Coifman[3]基于双线圈检测器数据和交通流理论,通过在时空图中估计路段行程时间重构车辆轨迹.Rao 等[4]利用车牌识别数据构建了一种车辆路径重构方法,进一步可基于路径对交通网络的历史OD(original-destination)进行估计. Hao 等[5]、Wan 等[6]、Shan 等[7]基于概率论的思想,分别采用随机模型、期望最大化算法(expectation-maximum,EM)及最大似然估计,从微观角度重构浮动车任意相邻采样点之间的运动轨迹. Li 等[8]提出了基于K 最近邻回归算法利用不完整轨迹来扩充轨迹样本量. Xie 等[9]基于修正的交通信号配时方案、车辆通过时间和车辆行程时间构建微观仿真环境,实现了对干道车辆轨迹重构. Mehran 等[10]通过融合秒级浮动车数据、音视频数据(audio video interleaved,AVI)及信号控制参数,提出了一种基于变分理论城市干道车辆运行轨迹估计方法,并利用东京一条包含五个交叉口的单行道实测数据进行了方法验证和误差分析. 唐克双等[11]通过融合视频和定点检测器流量数据,基于交通流理论和交通仿真思想,构建了一种不依赖高频浮动车数据,适用于多车道的轨迹重构方法. 综上分析可知,现有研究均能够对车辆轨迹数据进行有效重构,但均只考虑了人工驾驶环境,未考虑未来智能网联混合交通流的情况. 随着智能网联技术的发展,CAV 除了能提供自身轨迹数据外,还能通过感知设备(摄像头和雷达)提供自身一定范围内的车辆轨迹数据. 因此,CAV 采集的移动传感数据将会给轨迹重构提供一种新的思路. 如何充分考虑混合交通流环境下不同车辆类型提供的数据,构建全样本车辆轨迹重构模型,是未来CAV 环境下车辆轨迹重构亟待解决的关键问题.
为解决该问题,本文拟研究混有RV、CV 和CAV 的混合交通流全样本车辆轨迹重构方法. 充分利用CAV 和CV 提供的轨迹数据信息,提出基于跟驰特性的混合交通流轨迹重构模型,并通过仿真试验验证模型在不同交通流密度和CAV 渗透率条件下的合理性与有效性.
1 跟驰特性分析
在本文研究中,不考虑车辆换道的影响,选取较为简单的场景来阐述轨迹重构思想. 在微观交通流分析中,一般采用跟驰模型描述车辆之间的跟驰行为. 该模型认为当前车辆是否加减速与本身速度、前后车速度差和位置差有关. 因此,在已知部分轨迹的情况下,采用该模型可分析相邻轨迹中存在其他车辆轨迹的可能性.
跟驰模型主要可分为五种类型:刺激反应模型、安全间距模型、社会力模型、优化速度模型和低阶线性模型[12],均可作为本文轨迹重构的基础模型. 而作为社会力模型的一种,智能驾驶员模型(intelligent driver model,IDM)能够很好地描述熟练驾驶员的驾驶习惯,应用范围更广. 因此,本文以IDM 为例描述车辆之间的跟驰特性,如式(1)所示.

2 基于IDM 的车辆状态估计
2.1 数据环境分析
本文研究的混合交通流中有三种类型的车辆:RV、CV 和CAV. 其中,CAV 除提供自身的轨迹数据外,还可通过感知设备获取周围一定范围内的车辆位置和状态信息,因此,能提供周围一定范围内车辆的轨迹数据. 混合交通流中不同车辆组成如图1所示. CAV 探测范围内的车辆信息均可采集,不论是RV 还是CV. CV 由于不具备感知设备,所以只能提供自身的轨迹数据. 而RV 由于其不具备或未打开联网功能,所以既不能提供自身的轨迹数据,也不能提供周围车辆的轨迹数据.

图1 混合交通流中不同车辆组成Fig. 1 Composition of different types of vehicles inmixed traffic flow
从以上分析可知,在该混合交通流环境下,主要需要对CAV 探测范围之外的RV 进行轨迹重构.混合交通流轨迹时空图如图2 所示. CAV 两辆(CAV1、CAV2),CV 三辆(CV1、CV2、CV3);将阴影区域A中前一辆CAV 探测到的最后一辆车记为Vn−1,后面一辆CV 记为 Vn;红色虚线表示CAV 轨迹;蓝色点线表示CV 轨迹;黑色实线表示RV 轨迹;阴影区域A和B即为需要重构轨迹的区域. 在跟驰模型中,本车的跟驰行为主要与前车有关,即前车的轨迹直接影响本车的轨迹. 以阴影区域A为例,若区域A中无其他车辆,Vn会跟随 Vn−1,本车 Vn与前车 Vn−1构成跟驰行为,可采用跟驰模型进行描述.但若区域A中还存在未被观测的RV,则本车 Vn用跟驰模型计算的加速度会与实际加速度存在较大差异. 因此,构建轨迹重构模型试图寻找区域A内的最佳轨迹条数,来实现这种差异的最小化.
CV 提供的轨迹数据可分为是否在CAV 的检测范围内. 当CV 在CAV 的检测范围内,如图2 中的CV1 和CV3,这两辆车的轨迹可直接由CAV 观测,故该车提供的数据有无对整个模型的求解没有影响. 当CV 不在CAV 检测范围内时,如图2 中的CV2,此时需要利用该轨迹和CAV 提供的轨迹重构阴影区域A和B中的车辆轨迹.

图2 混合交通流轨迹时空图Fig. 2 Spatio-temporal diagram of mixed traffic flow trajectories
2.2 估计插入车辆的速度
车辆时空轨迹示意如图3 所示,图中:A1,A2,···,Ak为时空区域;k为时间总步数;Δt为时间步长;xn(Δt)为 Δt时 Vn的位置. 考虑到交通流稳定时,前后车的速度差别较小. 因此,第k个时空区域Ak中车辆 Vn的速度vn的估计如式(2)所示[13].


图3 车辆轨迹示意Fig. 3 Schematic diagram of vehicle trajectories
由于插入的RV 在区域Ak中,因此,该车在时刻kΔt的速度可以用区域Ak的速度v(Ak) 进行估计.
2.3 估计插入车辆的位置
在任意时刻,插入车辆的位置都需满足与前后车之间的安全间距. 因此,将Vn前插入的第i辆车记为 Vn,i,Vn,i的位置xn,i只能出现在一定的区间范围内,如式(3)所示.

当xn,i(t)在可行域内取不同的值时,Vn会得到不同的加速度. 而当估计加速度aˆn(xn,i(t))与实际加速度an(t) 最接近时,对应的xn,i(t) 即为要插入车辆Vn,i的位置.

综上,该优化模型的目标函数为式(4),约束条件为xn,i和aˆn(xn,i(t)) ,为典型的非线性优化模型,可用MATLAB 自带的函数直接进行求解.
3 基于IDM 的车辆轨迹重构
由第2 节的分析可知,得出插入车辆后,可由模型计算其插入的位置和速度. 因此,车辆轨迹重构模型即为需要寻找已知轨迹中间未知轨迹的数量,插入车辆轨迹示意如图4 所示. 当插入车辆数已知时,可采用第2 节中的方法依次求得每辆插入车辆轨迹的具体位置和速度. 考虑到车辆之间的最小安全间距,插入车辆数m的最大可能取值为N,如式(5)所示.

图4 插入车辆轨迹示意Fig. 4 Schematic diagram of inserted vehicle trajectories

在估计插入的速度和位置后,可重构 Vn,m的轨迹. 根据IDM 由 Vn,m的轨迹可求出 Vn的加速度.插入m辆RV 后代入式(1)可计算 Vn的理论加速度.
此处,选用 Vn加速度的均方根误差作为衡量标准,则均方根误差最小时对应的m即为最佳插入的车辆数,如式(8)所示.

因此,该问题也为一个非线性优化问题,目标函数为式(8),约束条件为式(1)、(6)、(7). 综上,当确定最佳插入车辆数量以后,可采用第2 节中的方法对每一插入车辆轨迹进行精确地重构.
4 数值仿真分析
4.1 仿真参数设置
为验证模型的有效性,基于IDM 设计元胞自动机进化规则,模拟单车道高速公路交通流运行规律.所有车辆之间跟驰行为均用IDM 描述[14−15]. 仿真路段长度1000 m,元胞长度0.1 m,仿真时间1000 s,仿真步长1 s. 为使仿真数据更趋向于真实数据,在仿真过程给车辆设置随机减速模拟真实道路上的车流运行状况.
本文共设计两种基准试验方案,第一种方案是将CAV 的渗透率恒定为8%,CV 渗透率恒定为20%,改变试验中的交通流密度,研究不同交通流密度对模型的影响. 第二种方案将交通流密度设定为70 辆/km,改变CAV 和CV 的渗透率,研究不同渗透率对模型的影响. 本文IDM 的参数[16]取值为:s0=2 m,aM=1 m/s2,T=1.5 s,b=2 m/s2,l=4.5 m.
4.2 交通流密度的影响
为研究道路上交通流密度对本文模型结果的影响,将CAV 和CV 的渗透率分别设定为8%和20%.首先,可基于仿真试验获取路段的流量-密度-速度关系如图5 所示.

图5 流量-密度-速度关系Fig. 5 Relationship between volume,density and speed of traffic flow
由图5 可知:仿真路段中的最佳密度为40 辆/km,即当交通流密度大于40 辆/km 时,路段上的车辆开始出现拥挤;当交通流密度大于70 辆/km 时,车辆的平均速度低于20 km/h,而高速公路中很少出现车辆速度小于20 km/h 的情况. 因此,为研究本文模型在不同交通状态下的重构效果,此处将交通流密度设为20、30、40、50、60、70 辆/km. 为避免随机因素的影响,同一交通流密度下采用不同的随机种子进行仿真和轨迹重构,取其平均值作为最终结果. 轨迹重构图像示例如图6 所示. 不同交通流密度条件下求得的插入车辆数如表1 所示.

图6 交通流密度为60 辆/km 时轨迹时空图Fig. 6 Spatio-temporal diagram of the trajectories when traffic flow density is 60 veh/km
由表1 可知:当交通流密度小于等于40 辆/km 时,会出现插入的车辆数小于实际车辆数;而当交通流密度大于40 辆/km 时,则出现插入的车辆数大于实际车辆数. 从百分比误差来看,当出现拥堵前,随着交通流密度的增加,模型求得的插入车辆数的误差逐渐减小,插入辆数的百分比误差也逐渐减小;当出现拥堵后,随着交通流密度的增加,模型求得的插入车辆数的误差逐渐增加,插入辆数的百分比误差也逐渐增大. 分析可知,开始拥堵之前,大多数车辆自由行驶,且车辆之间相互干扰较少,所以误差较大.开始拥堵后,当两辆车之间插入的车辆数较大时,模型求得的插入车辆数会产生一定的误差. 随着交通流密度的增大,车辆之间的间距逐渐减小,出现两辆车之间插入的车辆数较大的情况增多,故插入辆数的误差逐渐增大.

表1 不同交通流密度条件下插入车辆数估计Tab. 1 Estimation of the numbers of inserted vehicles under different traffic densities
当交通流密度小于60 辆/km 时,本文模型求得的插入车辆数的误差小于1 辆,误差小于10%. 综上分析可知,本文模型求得的插入车辆数较为准确,适用于高速公路的各种交通状态.
为进一步评估本文模型的轨迹插入效果,选用每一时刻插入车辆的实际和估计位置之间的平均绝对误差(MAE,eMAE)、平均绝对百分比误差(MAPE,eMAE)和均方根误差(RMSE,eMAE)表征重构轨迹的准确性,分别如式(9)~(11)所示.

式中:xˆ(t)为插入车辆的估计位置;x(t)为插入车辆的实际位置.
根据式(9)~(11),可得不同交通流密度下的误差值,如表2 所示. 由表2 可知:当交通流密度为20 辆/km 时,由于需要插入的车辆数过少,所以重构轨迹车辆位置的平均绝对误差相较其他密度较高.当交通流密度大于20 辆/km 时,重构轨迹车辆位置的误差随着交通流密度的增大而增加,但变动幅度不大. 在不同的交通流密度条件下,重构轨迹车辆位置的平均绝对误差的平均值为12.97 m,平均绝对百分比误差的平均值为0.37%,均方根误差的平均值为19.55 m. 从整体上来说,本文模型在不同交通流密度下重构轨迹车辆位置的误差较为稳定.

表2 不同交通流密度条件下轨迹重构误差Tab. 2 Trajectory reconstruction error under different traffic density conditions
4.3 CAV 和CV 渗透率的影响
CAV 和CV 提供的数据作为模型的已知数据,研究其渗透率对模型结果的影响尤为重要.
4.3.1 CAV 渗透率的影响
为研究不同CAV 渗透率对模型结果的影响,将交通流密度设为70 辆/km,CV 渗透率设为20%.CAV 的检测范围设为100 m. 若车辆在道路上均匀分布,则CAV 检测范围包含7 辆车. 但考虑到车辆的随机分布和感知设备的误差,此处假设CAV 能记录检测范围内车辆数为6. 将CAV 渗透率分别设置为4%、6%、8%、10%、12%和14%,研究不同渗透率下的车辆轨迹重构效果,其中,插入车辆数估计误差如表3 所示,轨迹重构结果示例如图7 所示.

图7 CAV 渗透率为14%时轨迹时空图Fig. 7 Spatio-temporal diagram of the trajectories whenCAV penetration rate is 14%
由表3 可知:当道路上的交通流密度为70 辆/km时,随着CAV 渗透率的增加,需要插入的车辆数减少,轨迹重构的难度减小,求出的插入车辆数的误差和百分比误差均逐渐减小;当渗透率只有4%的情况下,模型也能够较好地估计插入轨迹的数量. 因此,本文模型在未来不同渗透率环境下均能很好应用.进一步,可计算重构轨迹车辆位置误差如表4 所示.

表3 不同渗透率条件下插入车辆数估计Tab. 3 Estimation of the numbers of inserted vehicles under different CAV penetration rates
由表4 可知:当道路上的交通流密度为70 辆/km时,随着CAV 渗透率的增加,重构轨迹车辆位置的误差逐渐减小,即本文模型的准确性逐渐提高. 以MAE 为例,当CAV 的渗透率在4%~8%范围内时,平均每增加一辆CAV,平均绝对误差减小1.12 m.当CAV 的渗透率在8%~14%范围内时,平均每增加一辆CAV,平均绝对误差减小0.73 m. 因此,当CAV 渗透率大于8%时,平均绝对误差趋于稳定.

表4 CAV 不同渗透率条件下轨迹重构误差Tab. 4 Trajectory reconstruction error under different CAV penetration rates
4.3.2 CV 渗透率的影响
将交通流密度设为70 辆/km,CAV 渗透率设为8%,研究CV 渗透率为16%、18%、20%、22%、24%时轨迹重构结果,如表5 所示.

表5 CV 不同渗透率轨迹重构结果Tab. 5 Reconstruction results of different CV penetration rates
由表5 可知:随着CV 渗透率的提高,插入辆数的误差逐渐减小,插入数量的百分比误差也逐渐减小,即轨迹重构效果不断提升. 此外,车辆位置的误差也越小,即轨迹重构的准确性有所提高.
为研究CAV 和CV 渗透率对试验结果的影响,以CAV 渗透率为横轴,CV 渗透率为纵轴,绘制均方根误差热力图,如图8 所示.
由图8 可知:均方根误差趋势为随着CAV 或CV 渗透率的提高,轨迹重构效果逐渐变好. 但与CV渗透率相比,CAV 渗透率对结果的影响更大. 分析可知,增加一辆CAV 能够获得道路上多辆车的轨迹数据,而增加一辆CV,只能获取该车的轨迹数据.因此,当CAV 渗透率较高时,已知轨迹的车辆较多,此时CV 对试验结果的影响较小.
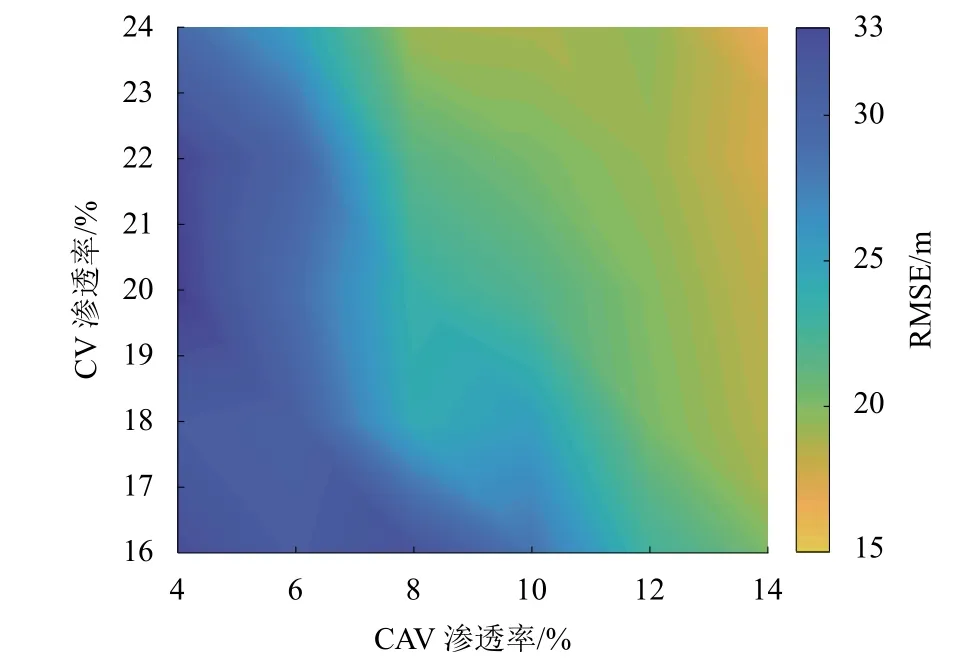
图8 均方根误差热力图Fig. 8 Heat map of RMSE
5 结 论
1) 在出现拥堵前,随着交通流密度的增加,本文模型求得的插入车辆数的误差逐渐减小;而在出现拥堵后,随着交通流密度的增加,本文模型求得的插入车辆数的误差逐渐增大.
2) 本文模型重构轨迹车辆位置的平均绝对误差在不同的交通流密度条件下均在可接受范围内,即本文模型在不同的交通流密度下均能较为准确地重构所有车辆的轨迹.
3) 重构轨迹的准确性随着CAV 和CV 渗透率的增加而提高. 与CV 渗透率相比,CAV 渗透率对结果的影响更大. 且当CAV 渗透率较低时,本文模型也能较好地重构所有车辆的轨迹.
本文证明了基于跟驰特性的车辆轨迹重构模型的有效性,但选取的场景简单,仅研究了单车道高速公路车辆轨迹重构模型,未来将结合换道模型,研究智能网联环境下多车道车辆轨迹重构模型.
致谢:西南交通大学综合交通大数据应用技术国家工程实验室交大数科创新中心项目(JDSKCXZX-202003)和重庆交通大学重庆市交通运输工程重点实验室开放课题(2018TE01)的资助.
