由拉普拉斯变换求傅里叶变换方法的研究
2021-12-28陆三兰
宋 琪,陆三兰
(华中科技大学 电子信息与通信学院,湖北 武汉 430074)
在“信号与系统”课程中,傅里叶变换和拉普拉斯变换都是重要的教学内容.一般来说,傅里叶变换的学习难度更大一些,因为一些不满足绝对可积条件的信号,它们的傅里叶变换不是根据定义或者用傅里叶变换的常用性质获得的,而是采用了一些特殊方法,学生们往往难以掌握.绝大多数“信号与系统”教材总是将傅里叶变换的内容安排在前面,而将拉普拉斯变换放在后面,因此利用拉普拉斯变换求傅里叶变换的方法往往被忽视了.实际上,由于拉普拉斯变换与傅里叶变换之间存在普遍性与特殊性的关系,故利用拉普拉斯变换求傅里叶变换也不失为一种有效的方法,当然具体使用时还需要注意使用条件.
1 拉普拉斯变换与傅里叶变换的关系
连续时间信号x(t)的傅里叶变换定义为[1]

x(t)的拉普拉斯变换定义为

对比式(1)与式(2)可知,x(t)的拉普拉斯变换与傅里叶变换的表达式有如下关系:

由于s=σ+ jω,只有当σ= 0时,才有s=jω,故式(3)成立的条件是:X(s)的收敛域(ROC)必须包含s平面的虚轴(即σ= 0).也就是说,利用拉普拉斯变换求傅里叶变换必须满足此条件.有必要说明一点,式(2)定义的是双边拉普拉斯变换,其收敛域可能是s平面上的一个右半平面、左半平面、垂直带状区域或者是全平面.根据函数X(s)的收敛域是否包含虚轴(jω轴),利用拉普拉斯变换求傅里叶变换可分为三种情况: (1)若X(s)的收敛域不包含虚轴且收敛边界不在虚轴上,则信号x(t)的傅里叶变换不存在; (2)若X(s)的收敛域包含虚轴,则信号x(t)的傅里叶变换存在,且X(jω)的表达式与X(s)的表达式之间具有式(3)所示关系; (3)若X(s)的收敛域不包含虚轴但收敛边界位于虚轴上,则X(jω)可能存在,但X(jω)与X(s)的表达式之间并非如式(3)所示那样简单直接的替换关系.
2 利用拉普拉斯变换求傅里叶变换
2.1 X( s )的收敛域包含虚轴
这种情况下信号的拉普拉斯变换很容易获得,直接将拉普拉斯变换表达式中的s替换成jω便可得到傅里叶变换.
例1求x(t) =sin( πt)[u(t) -u(t-10)]的傅里叶变换.
解x(t)是时限信号,即其值只是在有限区间t∈[0,10]内不为零,故其拉普拉斯变换的ROC 是全s平面,可先求出X(s),再转化成X(jω).下面先求其拉普拉斯变换.
因x(t)可表示为x(t) =sin( πt)u(t) -sin(π(t-10))u(t- 1 0),由变换对
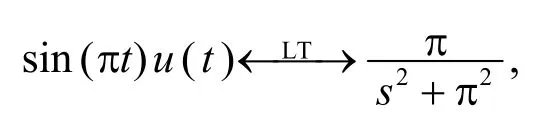
并利用时移性可得
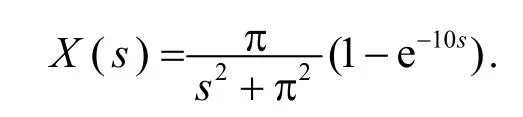
然后可由式(3)得到
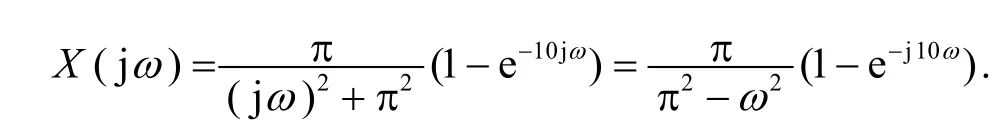
此题如果直接按照定义计算积分会比较麻烦,而通过拉普拉斯变换的表达式转化成傅里叶变换的表达式则非常方便快捷.
2.2 X( s )的收敛边界在虚轴上
当s平面的虚轴不在X(s)的收敛域内部,而是收敛域的边界时,这种情况下若傅里叶变换存在,其表达式包含冲激函数,不能直接由式(3)得到.
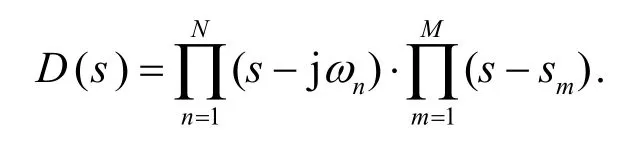
这里极点jωn位于虚轴上,极点sm位于虚轴的左侧或者右侧.对有理函数X(s)部分分式展开后得

对式(4)进行拉普拉斯逆变换,若X(s)的ROC 是右半平面,则x(t)具有如下形式:
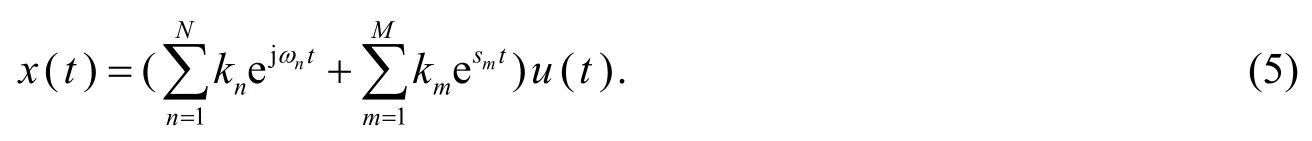
若X(s)的ROC 是左半平面,则x(t)具有如下形式:
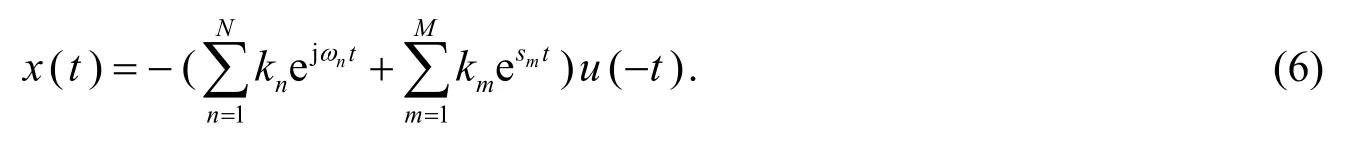
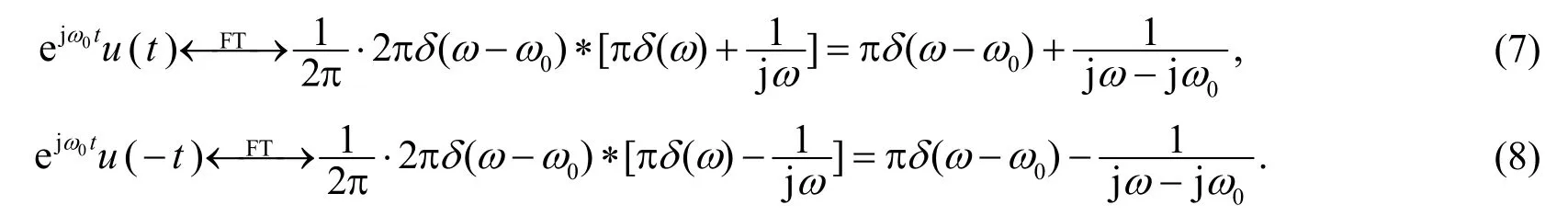
故式(5)和式(6)的傅里叶变换分别是
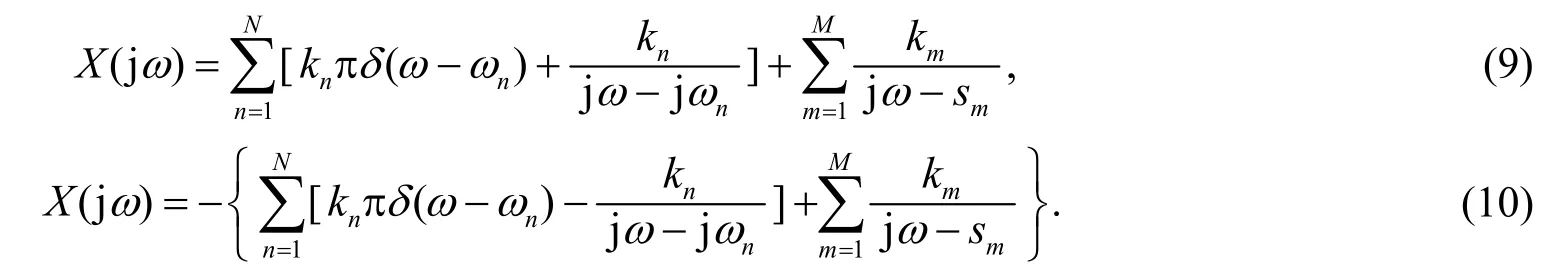
式(9)是当 X(s) 的ROC 是右半平面时,根据 X(s) 的部分分式展开式求得的傅里叶变换公式; 式(10)是当 X (s) 的ROC 是左半平面时,根据 X(s) 的部分分式展开式求得的傅里叶变换公式.
例2利用x(t) =e-tu(t)+u(t)的拉普拉斯变换求其傅里叶变换.
解x(t)是右边信号,且有一个极点0s= 位于虚轴上,于是由式(9)有
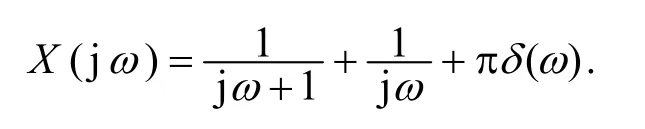
例3求x(t) =cos(πt)u( -t)的傅里叶变换.
解x(t)是左边信号,由于cos( πt)u( -t) =cos(- πt)u( -t),且,从而X(s) =于是由式(10)有

2.3 X( s )在虚轴上有高阶极点
上一小节详细推导了 X(s)在虚轴上有简单极点的情况下,如何由拉普拉斯变换求得傅里叶变换公式.当 X(s)在虚轴上有高阶极点时,文[2]认为傅里叶变换表达式中包含冲激函数的导数.从傅里叶变换的物理意义是信号的频谱密度函数这个角度来考虑这个问题,当频谱密度函数中包含冲激函数,就意味着信号包含的某个频率(冲激所在频率点)具有非零的有限大小的幅度(例如直流信号,或者周期函数包含的谐波的振幅).冲激函数的导数即冲激偶,是强度为无限大的一对冲激,根据数学上导数的定义可以将频谱密度函数中包含的冲激偶理解为信号包含的某个频率的振幅为无穷大,这样的信号在实际工程中是不存在的,因此冲激函数的导数没有工程意义[3].因而不必考虑虚轴上有高阶极点的情况.
3 结束语
在求信号的傅里叶变换时,只要条件满足,适当利用拉普拉斯变换可以有效减少计算或化简的运算量,提高正确率.
