外壁流线型分压工具结构参数优化分析*

宋兴良 孙英 王玉宏

（1.大庆油田有限责任公司采油工程研究院；2.黑龙江省油气藏增产增注重点实验室；3.大庆油田有限责任公司天然气分公司；4.大庆油田技术监督中心）

随着油田开发不断深入，我国大部分油田相继进入高含水阶段，开采难度逐年增大[1-3]。目前，大庆油田三次采油开发对象由一类油层逐渐转向二、三类油层，层间差异更大，单层注入量由50～70 m3/d下降到10～50 m3/d。目前化学驱分注技术存在一定的不适应性。由于在低注入量条件下，聚合物驱溶液流速相对较低，流动状态及水力特性发生变化，导致外壁流线型分压工具很难建立有效节流压差，无法满足现场单层注入量较低层段的注入需求。因此，对现有外壁流线型分压工具进行结构优化，提高低注入量情况下的节流压差，同时黏度损失又不超过现场要求[4]。

1 几何模型建立

根据节流原理，溶液在流过变截面时会产生节流压差，压差变化受截面形状影响。聚合物溶液在外壁流线型分压工具的作用下产生节流压差。为了匹配原壁流线型分压工具结构特点，基本结构与原壁流线型分压工具保持一致，主要结构参数如图1所示。外壁流线型分压工具流域模型见图2，深蓝色部分为溶液流过的区域，即流域模型，空白部分为分压工具的节流部分，不同结构参数分压工具的流域模型不同，对介质流经节流部分的影响也不同。

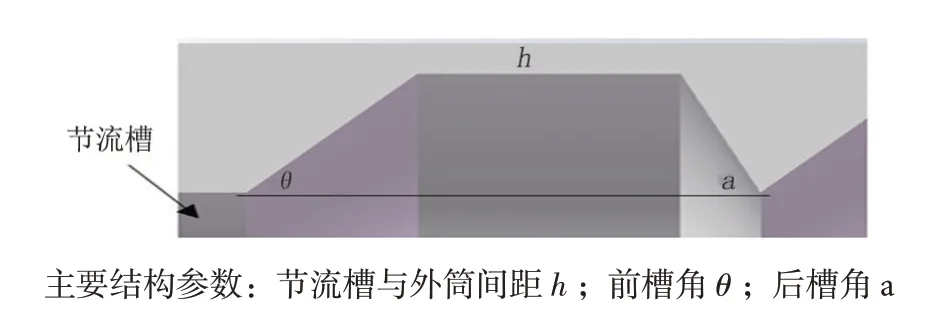
图1 分压工具主要结构参数

图2 分压工具流域模型

2 数值模拟研究

2.1 压降数学模型建立

由于聚合物溶液为典型的非牛顿流体，且经过拟合后的流变曲线符合幂律流体的流动特性[5-6]。

根据环形柱坐标系，R0为外筒半径，Ri为内筒半径，在环形空间中取长为L，内径为(Ro+Ri)2-r，外径为(Ro+Ri)2+r的环形流束来分析。

根据压力与切应力的平衡关系推导所得环空流道的流变公式改为变截面的公式：

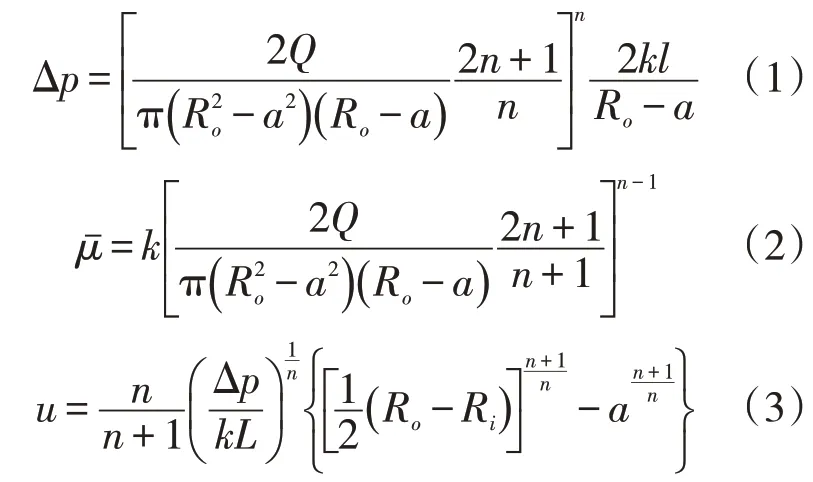
式中：Δp为进口端与出口端的压差，MPa；Q为流量，m3/s；a为变截面内径，mm；n为流体非牛顿性强度系数；k为聚合物平均黏度系数；L为圆管长度，m。

2.2 湍流模型的选择

由于分压工具整体尺寸较小，溶液在节流槽的作用下产生节流效应，溶液所受剪切程度越大，速度变化越大，涡流耗散则越严重。由于各湍流模型的适用范围不同，考虑经过分压工具流动属于无规则湍流运动，基于大量文献调研和经验积累，采用RNGk-e模型进行模拟，具有较高的计算精度[7-8]。

2.3 流变模型建立

针对聚合物溶液在分压工具内流动的流场特点，在数值模拟中不考虑热力学过程，流体流动的基本控制方程不包括能量方程。假设分压工具流场的物理量不随时间变化，为定常不可压流动，不考虑重力[9]。建立的基本控制方程如下：

连续性方程：

动量方程：

式中：ρ为流体密度，kg/m3；ui为i方向流速，m/s；uj为j方向流速，m/s；p为流体微元上的压强，MPa；τij是由分子黏性作用而产生的作用在微元体表面上的黏性应力张量，MPa。

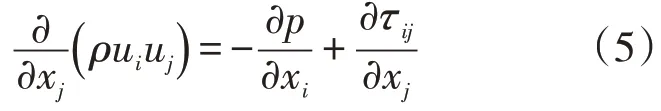
聚合物溶液属于非牛顿流体幂律定律，由非牛顿幂律流体的本构方程：

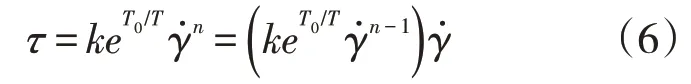
式中：τ为流体流动中的剪切应力，MPa；T0为参考温度，K；T为实际温度，K；γ̇为剪切速率，1/s。

FLUENT中还可以设置表观黏度的上下限，即：

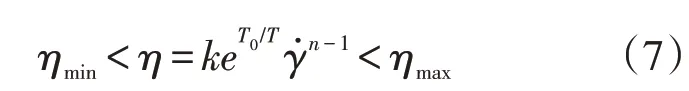
式中：η为表观黏度，Pa·s；k为流体的平均黏度系数（稠度系数）；n为流体非牛顿性强度系数（幂律指数）；ηmin和ηmax分别为幂律流体表观黏度的下限和上限。如果根据幂律流体模型计算得到的表观黏度超过了黏度的上下限，就用ηmin和ηmax的值代替计算出的黏度值。

2.4 有限元网格模型建立

建立完几何模型后，利用ICEM软件对分压工具的模型进行网格划分。采用四面体单元换分网格不仅可以减少计算量，还可以显著提高计算的稳定性和精度。通过对流道的三维几何模型的拓扑分析，将计算域分成若干可划分的单元网格的块，然后生成整体均为四面体单元的网格，在生成模型的整体网格时，为了对溶液在边界流动时的数值模拟更加精确，在分压工具的边界上设置边界层，分压工具的网格划分如图3所示。

2.5 边界条件和数值模拟过程

流场边界条件设置如下：入口边界：聚合物从入口进入分压工具环空流道，轴向速度u=Q/2A，水力直径DH=4Am/Cm计算，Am为入口截面积，Cm为湿周，湍流强度按5%取值，取出口压力为0 MPa，z=0截面设定为对称边界，固壁采用无滑移边界条件，壁面上u=0；壁面附近采用非平衡壁函数法。

由于环空间隙特别小，间隙内的流动属于近壁面流动，并且在间隙径向方向上流动参数变化剧烈，若使用传统的标准壁面函数，将会进一步增加误差[10]。对于此类问题，使用非平衡壁面函数将有更好的准确性。压力和速度的求解采用压力-速度耦合的SIMPLEC方法，代数方程采用超松弛法进行迭代求解。能量方程残差收敛标准设定为10-6，其他变量残差值的收敛标准均设为10-5。

3 流固耦合有限元分析

3.1 正交实验设计

压力降和黏度损失是衡量节流槽性能的重要参数，其影响因素很多，外壁流线型分压工具的槽距长度变量会对压降和黏损产生影响，对此先进行外壁流线型分压工具槽距对压降和黏损的影响见图4和图5。

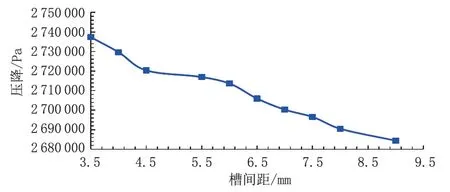
图4 槽间距对压降影响

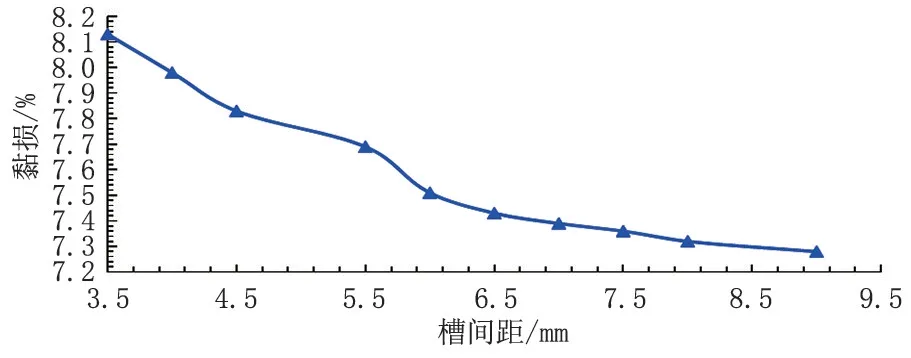
图5 槽间距对黏损影响

图4和图5中为流量为10 m3/d时聚合物溶液通过不同槽间距的外壁流线型分压工具的压降和黏损，当槽间距变化时，压降也随之变化，且槽间距越大，压降越大，但整体变化很小，但对黏损的影响较大，当间距超过6 mm时，黏损急剧增加，但对压降影响较小，所以为了简化正交实验的流程，选择槽间距为常数6 mm。所以对于外壁流线型分压工具来说，其主要作用的结构参数分压工具与外筒间距、前槽角、后槽角3个因素。

实验因素结构方案正交见表1，通过改变注入量的大小，模拟各流量下外壁流线型分压工具的压力降和黏度损失，最终优选出满足流量为10 m3/d时，压降下降超过1 MPa、黏损小于7%的最优结构参数组合。

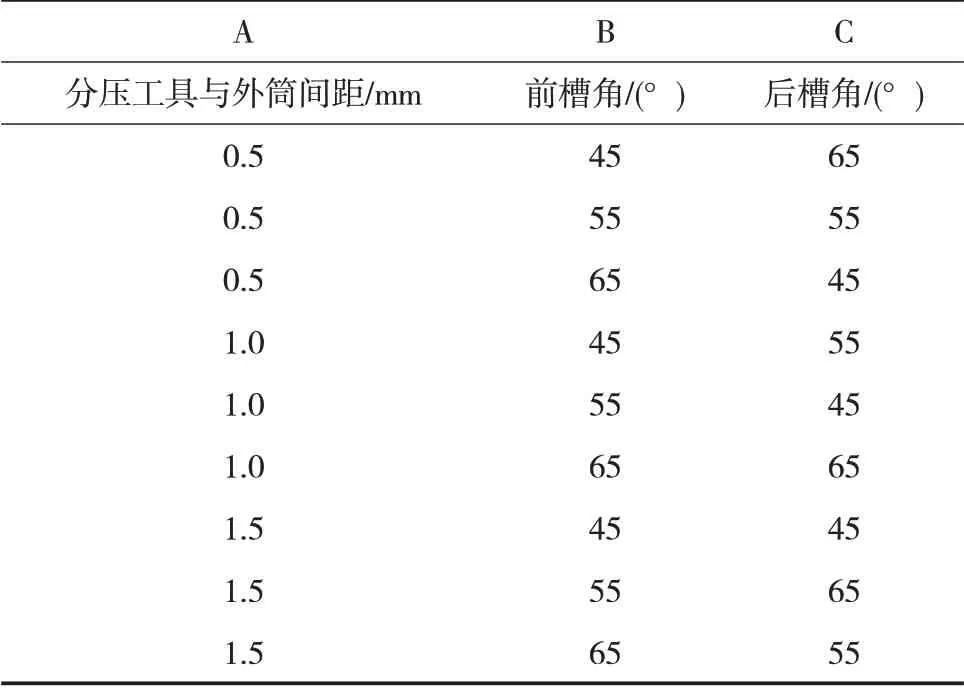
表1 实验因素结构方案正交

3.2 正交实验结果分析

当聚合物溶液高速流过外壁流线型分压工具时，由于速度梯度产生的剪切拉伸作用会导致聚合物溶液中聚合物分子发生机械降解，导致溶液黏度损失。流量10 m3/d时外壁流线型分压工具模拟结果见表2，随着各项影响因素的改变，压降和黏损均有不同程度的变化，其中压降变化范围在0.821～3.193 MPa，黏损在6.66%～7.51%。

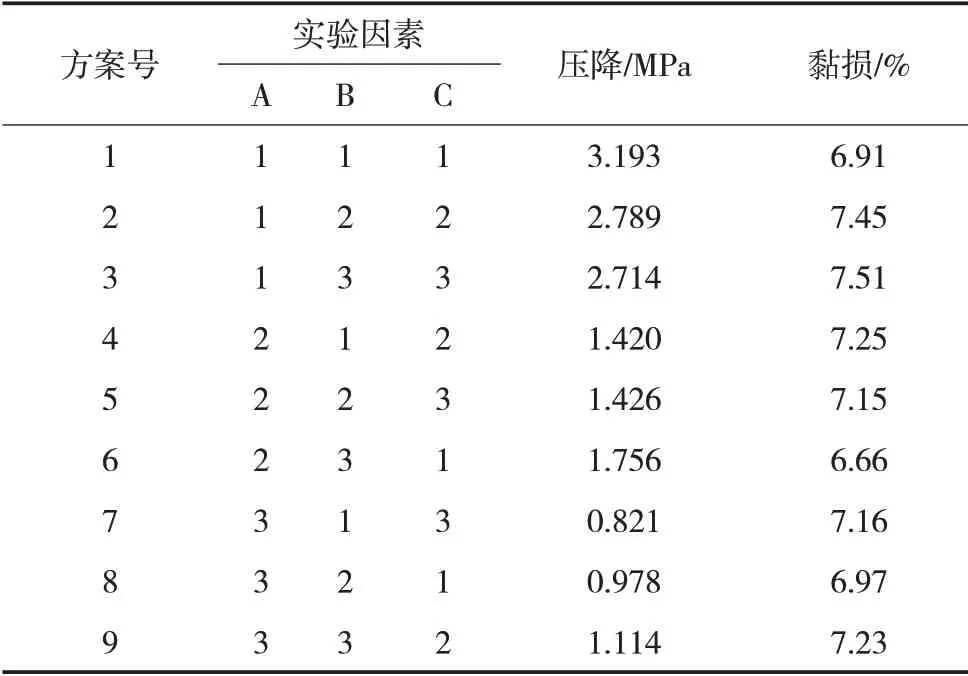
表2 外壁流线型分压工具模拟结果

运用综合平衡分析法来选择最优参数组合。分注工具各因素不同结构参数的压降及黏损的方差分析结果如表3和表4所示。

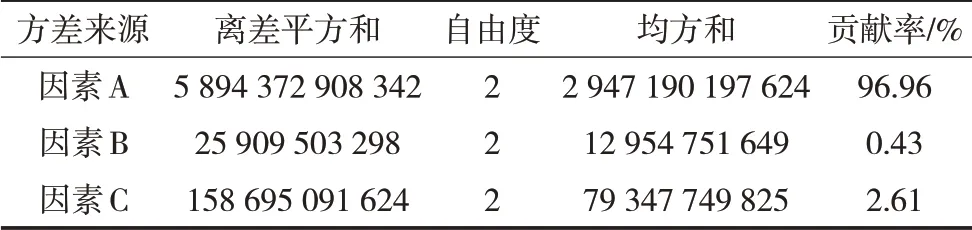
表3 压降的方差分析结果

表4 黏损的方差分析结果

由表3的分析可知：外壁流线型分压工具与外筒间距、前槽角、后槽角对压降影响的贡献率分别为96.96%、0.43%、2.61%。三个结构因素中外壁流线型分压工具与外筒间距对压降的影响最为显著占96.96%，前槽角及后槽角对压降的占比较小。

而外壁流线型分压工具与外筒间距、前槽角、后槽角对黏损影响的贡献率分别为21.47%、2.09%、76.44%。由此可知：外壁流线型分压工具的三个结构因素中，后槽角对黏损的影响同样最为显著占76.44%，而外壁流线型分压工具与外筒间距、前槽角对黏损的影响同样较为明显，分别为21.47%、2.09%。

根据方差分析结果，因素A对于压降与黏损的影响贡献率最大，这两个指标均随着A水平值的增大而增大，因此两个指标的选择出现了较大的矛盾，而由于分外壁流线型分压工具其最主要的作用是需要达到一定的压降，因此选择造成压降最大的结构参数即外壁流线型分压工具与外筒间距为0.5 mm；就因素B前槽角和因素C后槽角来看，其对于压降的影响相对较小仅为0.43%、2.61%，而对于黏损的影响较大为2.09%、76.44%，因此对于因素B前槽角和因素C后槽角，选择对减小黏度损失最有利的结构参数前槽角45°和后槽角65°。

通过方差分析方法和综合分析方法计算可知：若按照现场要求综合考虑压降与黏损的因素，为达到现场要求，则优选出的分压注入工具节流槽的最优结构参数为节流槽与外筒间距0.5 mm、前槽角45°、后槽角65°。

4 经济效果分析

依据优选结果对新型外壁流线型分压工具进行加工制造，并进行室内试验和现场应用，聚合物溶液流经新型分注工具时，在流量10 m3/d范围内，黏损率由原环形降压槽工具黏损8.2%降至7%，黏损得到较好改进。

2020年在大庆油田某聚合物区块开展现场试验2口井，共连通油井8口。采用该分注工具后，截止到2020年12月底，有效厚度动用比例最高提高9.7个百分点，中渗透层动用程度明显提高，薄差层得到有效动用。连通8口油井4个月累计产油量1 427 t，销售价格按2 758元/t，吨油操作成本按835元/t计算，经济效益274.41万元，分注贡献率按8%计算，取得经济效益21.95万元。

5 结论

1）针对聚合物驱分注井单层注入量较低时，采用原外壁流线型分压工具较难建立有效节流压差的问题，对外壁流线型分压工具的结构参数进行分析，推导建立了流体流过外壁流线型分压工具的压降和流变数学模型。

2）通过CAXA及ICEM软件建立外壁流线型分压工具三维模型，并进行网格划分，通过Fluent有限元分析获得聚合物溶液在不同结构参数外壁流线型分压工具中的流动特性，并结合综合平衡分析法对外壁流线型分压工具的结构参数进行优化，最终优化后的结构参数为外壁流线型分压工具与外筒间距0.5 mm、前槽角45°、后槽角65°。

3）模拟结果显示单层注入量10 m3/d时，节流压差由0.2 MPa提高到3.19 MPa，聚合物溶液黏损率小于7%，现场试验结果显示可有效提高中低渗透层动用程度，改善二、三类油层注入效果，具有良好的应用前景。