车体垂向振动对高铁FSO通信性能影响的研究
2021-12-28缪慧敏郭记涛吴茗蔚刘喜昂
缪慧敏,郭记涛,孟 婷,吴茗蔚,刘喜昂
(浙江科技学院 a.机械与能源工程学院;b.信息与电子工程学院,杭州 310023)
面对日益增长的交通需求,高速铁路(以下简称高铁)可作为缓解需求的一种重要解决方案,它具有绿色、环保、节能的优点[1]。截至2020年7月底,中国高铁运营里程达到14.14万km[2],根据2016年修订的《中长期铁路网规划》,预计2025年铁路网规模达到17.5万km左右[3]。随着高铁的快速发展,传统的无线射频(radio frequency,RF)技术因存在多普勒频移、带宽低、干扰强等缺点,已经不能满足人们高质量通信的需求。而自由空间光(free space optical,FSO)通信技术可对现有RF技术进行补充,它具有保密性好、抗电磁波干扰[4-5]、部署快捷[6]、不需要频谱许可证[7-8]等优点,不受多普勒频移的影响,并且有足够的带宽来满足数据传输需求。2007年,Kotake等[9]提出了一种在列车和地面之间使用FSO的地对车通信系统,并证明该系统是一种很有发展前景的列车通信系统。Fan等[10]和Mabrouk等[11]分别提出了旋转收发机和多发射机方案,可减少沿轨道部署的基站总数,从而降低了建设成本。Fathi-Kazerooni等[12]和Mohan等[13]分别提出了双波长和分段多波束2种覆盖模型,为列车与基站之间提供无缝连接和切换,因而提高了地对车通信系统性能。高铁地对车FSO通信链路与传统FSO通信链路最大的区别在于列车一直处在前进的运动状态中,并伴随着不可忽略且难以准确估计的机械振动。由于列车的运动方向和速度都是可控且已知的,所以可利用捕获、瞄准和跟踪(acquisition, tracking and pointing,ATP)系统[14-15]修正由于列车的前进运动导致的发射机与探测器在水平方向上的偏移,因此可假设长时间内水平方向上探测器处在发射机发出光束的中心。然而高铁车体垂向振动对通信链路所带来的影响鲜有研究提及,故本研究探索高铁车体移动过程中垂向位移的统计特性,并利用动态束腰控制方案来降低车体垂向振动对通信链路性能的影响。
1 地对车FSO通信链路
一个典型的高铁地对车FSO通信链路如图1所示,在铁轨的一侧建立基站安装发射机,在列车顶部放置接收机,发射机发出高斯光束被接收机接收。图1中:z为发射机与接收机之间的传输距离;ω0为z=0时高斯光束的光斑半径,即束腰;ωz为高斯光束的光斑半径。
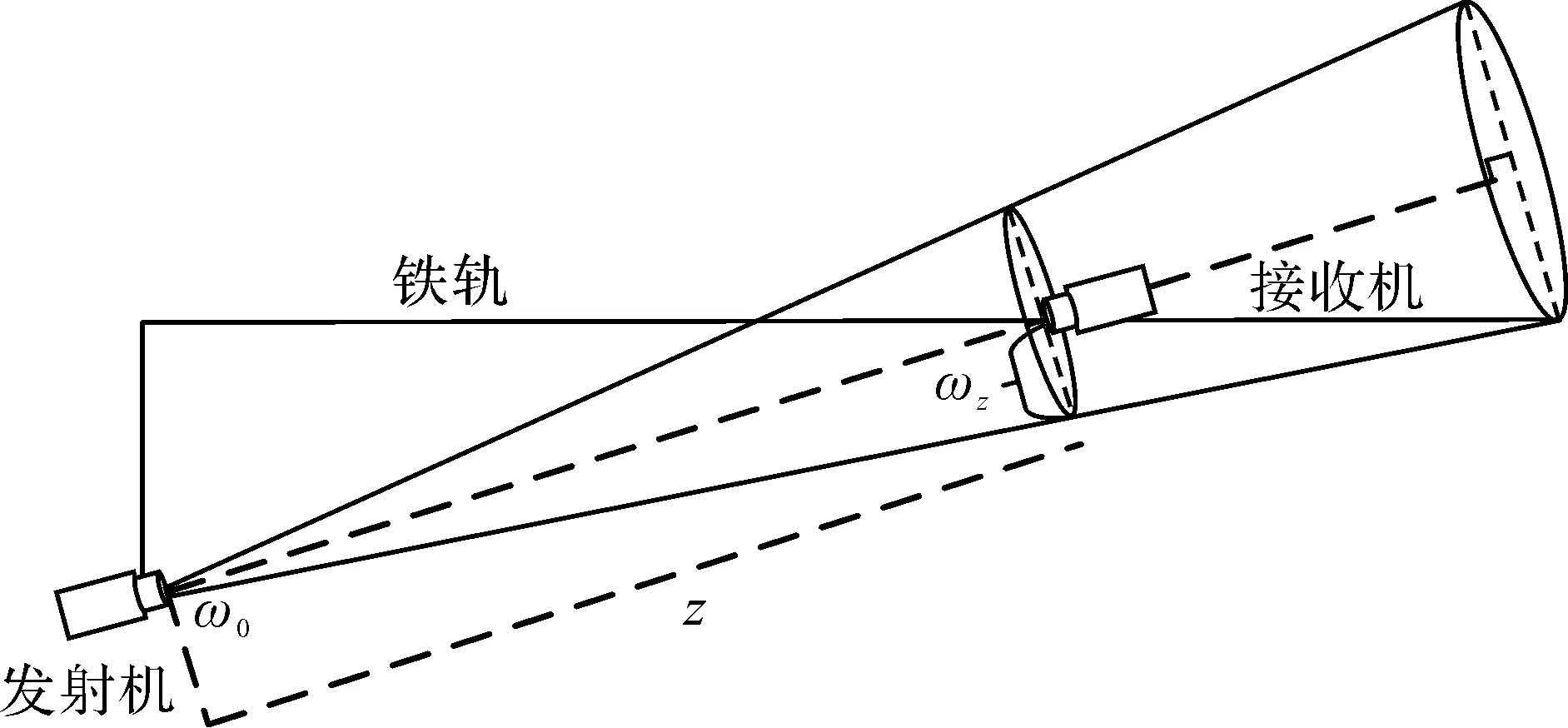
图1 高铁地对车FSO通信链路
根据高斯光束传输的特性,随着传输距离z的变化,高斯光束的光斑半径ωz表达式[16]11952为
(1)
式(1)中:λ为发射激光波长。图2为高斯光束截面,a为光学探测器C的半径;d为光学探测器C中心与高斯光束中心的偏移距离。在车体静止的情况下,d=0;在车体运动的情况下,列车前进会导致水平方向上的偏移,该偏移仅与前进时间t和车速v有关,为非随机变量,可利用ATP系统进行校准;相比车体垂向振动所导致的偏差,车体横向振动所导致的偏差较小[17],可忽略不计,因此d等价于高速列车车体垂向位移。将接收端光学探测器C接收功率和光斑总功率的比例定义为指向性误差hp,可用MarcumQ函数表示[18]为
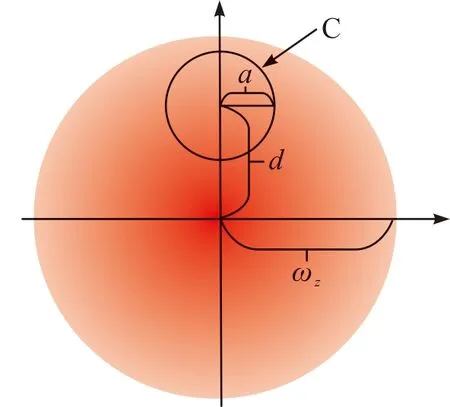
图2 高斯光束截面
(2)
2 车体垂向振动模型
2.1 轨道高低不平顺仿真
高铁轨道的轨面并非处于理想的平顺状态,列车行驶过程中带来的轨面的损耗、铁轨的焊接、路基的弹性不均匀等问题都会造成轨道不平顺[19]。通过大量实际数据的测量,已有针对不同轨道拟合出的功率谱密度(power spectral density,PSD)函数来描述轨道不平顺状态。以高速无砟轨道为例,其轨道高低不平顺表达式为S1(F)=A/Fm[20]1,F为空间频率,A、m为拟合系数,参数值及PSD函数曲线参见TB/T 3352—2014《中华人民共和国铁道行业标准》[20]2,4。为了进一步研究PSD函数,我们需要得到以频率f为变量的轨道高低不平顺表达式S2(f)。利用PSD函数在相应单位带宽中均方值相等(S1(F)dF=S2(f)df)的原理[21],再根据空间频率F、频率f及车速v之间的关系f=Fv,可得高速无砟轨道PSD函数的频域表达式为
S2(f)=Af-mvm-1。
(3)
通过估计功率谱的Blackman-Turkey法,有频谱模值与PSD函数之间的关系[22]140如下:

(4)
式(4)中:zv(n)为轨道高低不平顺时间序列;Zv(k)为zv(n)的频谱;DFT为离散傅里叶变换;Δf为频率采样间隔;N为时域与频域的采样点数。由于zv(n)为随机过程,其振幅相位皆具有随机性。设n(k)为复高斯白噪声,在式(4)频谱模值基础上乘以n(k),可得轨道高低不平顺频谱

(5)
取车速v=100 m/s,波长范围为2~200 m(即频率范围0.5~50 Hz),时间采样间隔Δt=0.001 s,采样点数N=214进行仿真。图3为高速无砟轨道的高低不平顺时域样本。

图3 高速无砟轨道高低不平顺时域样本
2.2 车体模型
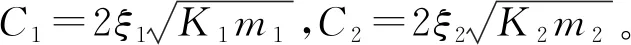

图4 1/4车体4自由度模型
根据D’Alembert’s原理,对车体所受动力进行分析,得到垂向振动微分方程组[23]56:
(6)
各悬架的详细参数见文献[23]58。
2.3 Simulink仿真模型
利用MATLAB软件中的Simulink工具搭建车体仿真模型(图5),其中图5(a)为根据式(6)所搭建的微分方程Simulink仿真模型。由于搭建模型的过程比较繁琐,当车体模型较复杂时,搭建模型的难度将会大大增加,因此我们利用车体垂向位移与轨道不平顺之间的传递函数来搭建车体的Simulink仿真模型,可降低搭建模型的难度。
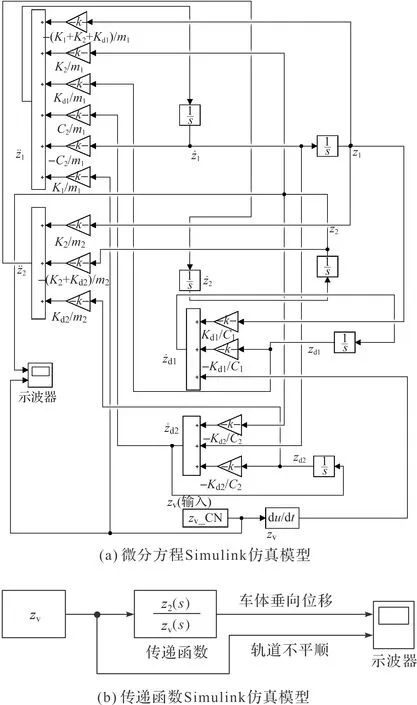
图5 Simulink仿真模型
利用拉普拉斯变换,将式(6)从实数域转换到复数域:
(7)
式(7)中,s为复变量。求解式(7)中Z2(s)与Zv(s)之比,即为车体垂向位移与轨道不平顺之间的传递函数
(8)
式(8)中:
图5(b)为根据式(8)建立的车体传递函数Simulink仿真模型。将2.1节所得的轨道高低不平顺仿真数值zv作为输入,经过车体传递函数Simulink仿真模型,可得输出车体垂向位移z2,轨道不平顺和车体垂向位移对比如图6所示。由图6可知,微分方程Simulink仿真模型与传递函数Simulink仿真模型输出的z2吻合,所以传递函数法也可得到z2,同时大大降低仿真复杂度。另外,z2比zv曲线变得光滑,这是为了乘客的舒适性,以最小化加速度为目的进行的模型参数优化。z2曲线变得光滑表明加速度减少,乘客舒适性提升。但在最小化加速度的情况下,z2幅值变化范围大于zv,因此需要分析z2对通信链路的影响。
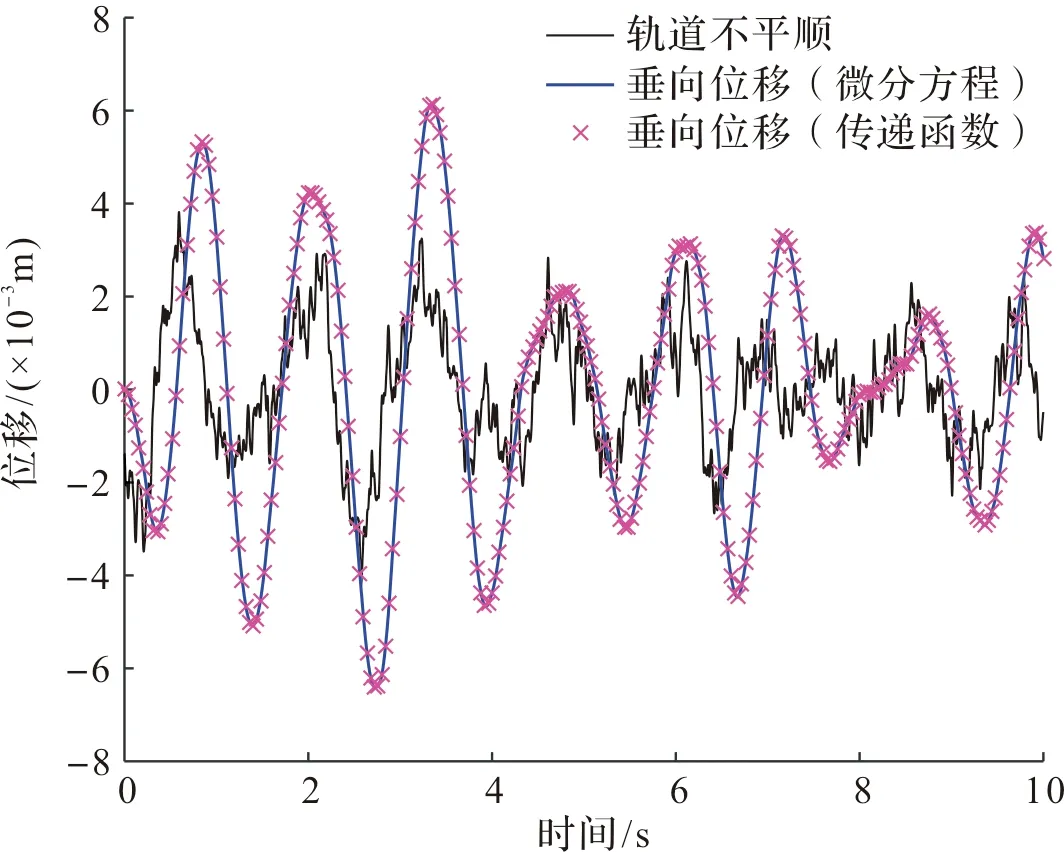
图6 轨道不平顺和车体垂向位移对比
2.4 垂向位移仿真数据的统计特性
对于2.3节的车体垂向位移离散序列z2(n),估计其均值[24]90为
(9)
估计其方差[24]159为

(10)
对车体垂向位移z2进行概率密度函数(probability density function,PDF)统计特性分析,车体垂向位移概率密度函数如图7所示。由图7可知,车体垂向位移PDF与高斯分布曲线重叠,由此可发现z2服从高斯分布。因此可定义z2的PDF:

图7 车体垂向位移概率密度函数
(11)
在2.1~2.3节的研究中,为了求得z2需要经过轨道不平顺仿真和车体模型仿真过程,中间的细节繁琐不便。但由z2的PDF可以通过仿真快速得到z2,中间过程大大缩短,减少了仿真时间。以N=225数量级为例,按照传统方法经轨道不平顺仿真、车体模型仿真过程得z2需约95 s,直接由z2的PDF仿真得z2需约0.5 s,仅为前者的0.53%,由此可见z2的PDF仿真法的优越性。另外,在高铁激光通信领域,通过z2的PDF可以推导指向性误差的PDF,这是信道建模的关键步骤,故有重要的研究意义。
3 动态束腰控制方案性能仿真
采用开关键控(on-off keying,OOK)调制方式,系统瞬时误码率[25]为
(12)
式(12)中:Q(·)为高斯Q函数;R为光学接收器响应度,取0.5;Pt为发射功率,取39.810 7 mW(16分贝毫瓦);N0为接收端噪声单边功率谱密度,取2×10-14A/Hz;Rdata为数据传输速率,取1 Gb/s[26]。
在考虑车体垂向位移z2的所有可能值情况下,利用式(11)~(12)可得系统平均误码率[16]11954

(13)
在传统的固定束腰控制方案中,ω0为固定值,在确定的传输距离下,ωz不变。根据式(13),取仿真参数z=1 km,a=10 cm,λ=1 550 nm[26],固定束腰控制方案下的系统平均误码率如图8所示。
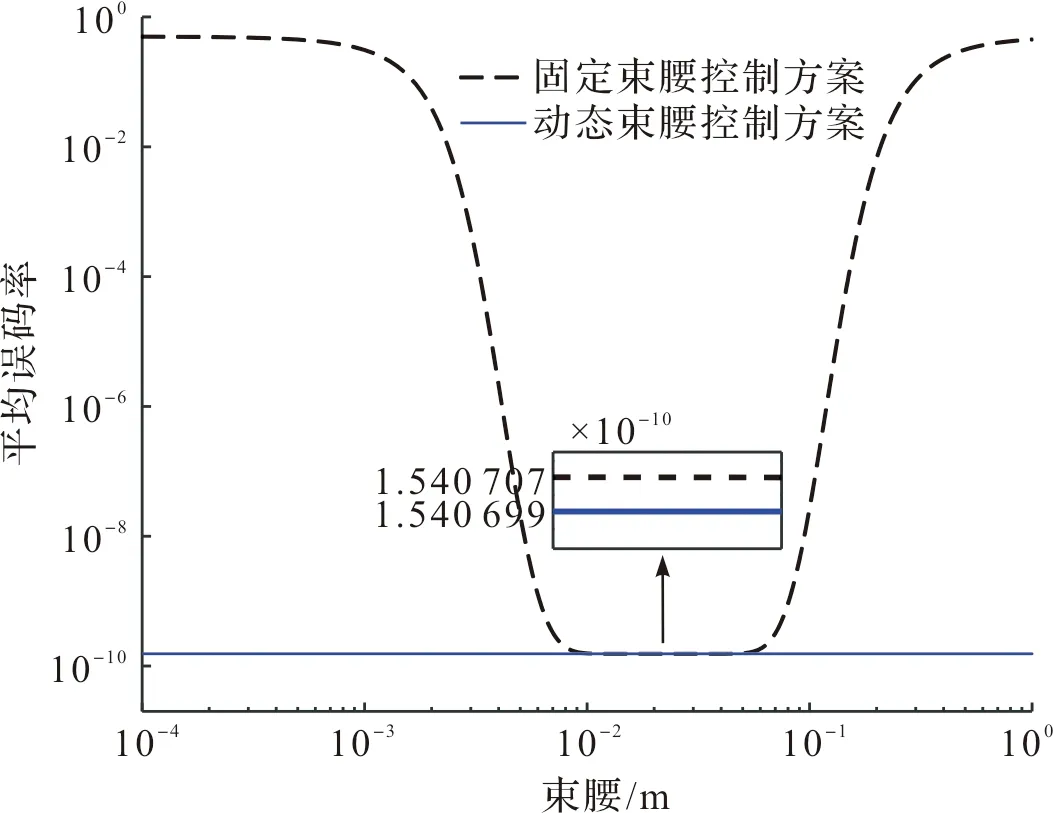
图8 固定及动态束腰控制方案下的系统平均误码率
在动态束腰控制方案中,ω0为动态数值,ωz随ω0而变化,文献[16]11956推导其ωz的最优值:
(14)

4 结 语
本文研究了高铁地对车通信系统,通过对车体进行垂向受力分析,利用拉普拉斯变换推导出车体垂向位移与轨道不平顺之间的传递函数,可以方便快捷地搭建车体传递函数Simulink模型,生成车体垂向位移数据。通过统计,进一步得出了车体垂向位移的概率密度函数表达式,简化了车体垂向振动位移的仿真。采用动态束腰控制方案,将其应用于高铁地对车通信系统,并通过仿真验证了本方案性能的优越性。
