基于自适应滑模观测器的PMSM 无传感器控制
2021-12-28赵仙花夏宇敬高兴超史振萍吴延霞
赵仙花,夏宇敬,高兴超,史振萍,吴延霞
(253023 山东省 德州市 德州学院 能源与机械学院)
0 引言
永磁同步电动机(Permanent Magnet SynchronousMotor,PMSM)因其结构简单、体积小、质量轻、功率密度高等优点,得到了广泛应用。近年来,永磁同步电机无传感器控制技术成为了国内外研究人员研究的热点[2-4]。目前实现高动态性能永磁同步电机控制的两种主流控制策略是矢量控制和直接转矩控制[1],其中矢量控制应用最广,最成熟。矢量控制系统的关键是转子位置和转速信息的准确获取,以前通常是采用机械传感器来获取转子位置和转速,这样不仅增大了系统的成本和体积,同时也降低了可靠性。
滑模观测器对内部参数变化不敏感、对外部扰动的鲁棒性以及对数学模型精度要求不高,适用于永磁同步电机位置和速度的估算方法[5],但是传统的滑膜观测器由于采用了高频切换开关函数,给系统带来了一系列问题,如抖动、鲁棒性差、趋近速度慢等,影响了系统控制精度,制约了其应用。
为了提高永磁同步电机无传感器控制系统的整体性能,本文在分析传统趋近律滑模结构的基础上,通过选取指数项、系统状态可变项和终端项并结合非奇异终端滑模设计了一种自适应非奇异终端滑模观测器。
1 永磁同步电机的数学模型
在不影响控制性能的前提下,为了简化分析,忽略磁路铁心的饱和,不计磁滞和涡流损耗影响,假设绕组中感应电势波形为正弦波[6],则在α-β静止坐标系下永磁同步电机电流方程可写为

反电动势方程:
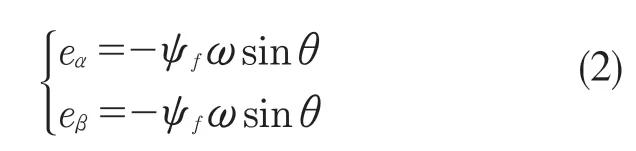
式 中:iα,iβ——定子电流α-β轴分量;uα,uβ——定子电压α-β轴分量;eα,eβ——反电动势α-β轴分量;Ls、Rs——定子电感和电阻;ψf——永磁体磁链;ω——电机角速度;θ——电机转子角位置。
由式(2)可得:

由式(3)和式(4)知,可通过估算滑膜观测器的反电动势来得到转子位置和转速信息,以实现电机的无传感器控制。
2 自适应非奇异终端滑模观测器
自适应非奇异终端滑模观测器实现框图如图1 所示。

图1 自适应非奇异终端滑模观测器实现框图Fig.1 Diagram of adaptive nonsingular terminal sliding mode observer
为获得反电动势估算值,根据静止坐标系α-β中的永磁同步电机数学模型构造滑模观测器:
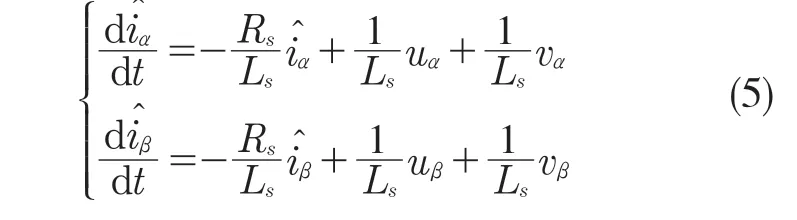
由式(5)减去式(1)可得定子电流偏差方程:
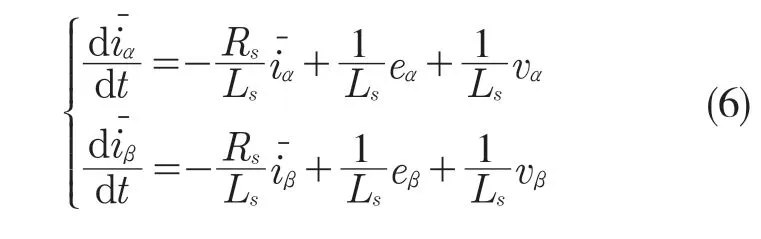
由式(6)整理得:

滑模控制器的设计通常分为:滑模面的选取、控制率的设计两部分。
2.1 滑模面的选取
定义非奇异终端滑模面S:

式中:λ>0;p,q——正奇数,1
2.2 自适应趋近律的设计
目前几种典型趋近律为等速趋近律、指数趋近律、幂指数趋近律和一般趋近律,由于对系统状态变量不能自动调整,其收敛性能不佳。合理的趋近律应该是当系统远离滑模面时,趋近速度增大,减少趋近时间,以满足系统动态响应。而当系统趋近滑模面时,速度逐渐降为零,以降低抖动。为改善控制性能,本文采用连续函数sigmoid()代替sgn(),将几种趋近律相结合并对其系数进行修正设计了一种自适应趋近律,使其能根据距离平衡点的远近自动调整趋近速度,提高系统性能。所设计的自适应趋近律为
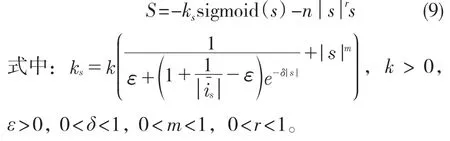
当滑模切换函数│s│增大时

当│s│减小时,

对于式(7),选取非奇异终端滑模面式(8),趋近律式(9),设计如下控制器,则电流误差系统将在有限时间内收敛到0,即满足=0,有
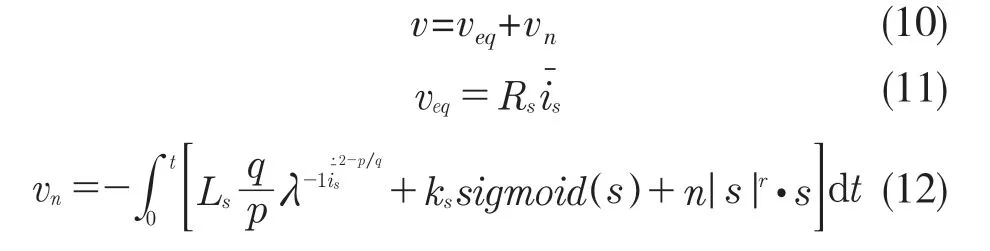
2.3 滑模存在和稳定性的证明
选取 Lyapunov 函数证明观测器稳定性

观测器误差方程(7)可简化为

由式(18)知,通过滑模控制律可以观测电机的反电动势,然后通过反电动势可以计算出转子位置和转速,以实现永磁同步电机无传感器控制。
3 仿真实验与分析
为验证自适应非奇异终端滑模观测器的可行性和有效性,在MATLAB/Simulink 中搭建其仿真模型。永磁同步电机无传感器控制采用idref=0 控制策略,控制系统原理图如图 2 所示。
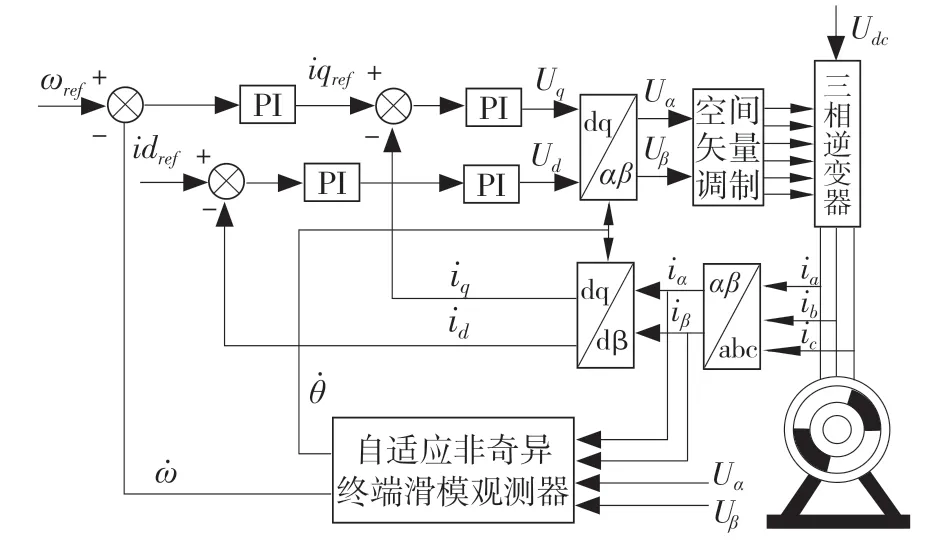
图2 控制系统原理图Fig.2 Schematic diagram of control system
仿真中电机参数有:极对数Pn=4,阻尼系数B=0,磁链ψf=0.1 Wb,转动惯量J=0.001 kg·m2,定子电感Ls=8.5 mH,定子电阻R=2.875 Ω。仿真条件有:直流侧电压Uab=311 V,PWM 开关频率fpwm=10 kHz,仿真时间t=0.2 s。因为搭建的模型较复杂,为了使仿真速度加快,选用定步长ode3(Bogacki-Shampine)算法,仿真步长为2×10-7s。参考转速设定为ωref=1 000 r/min。
图3 分别为传统滑模观测器下仿真得到的转子转速估计值与实际值的变化曲线、转子转速误差变化曲线、转子估算位置与实际位置的变化曲线和位置误差曲线。

图3 传统滑模观测器Fig.3 Traditional sliding mode observer
由图3 曲线可以看出,传统滑模观测器抖振比较大,且误差较大,精度低,系统性能差。
图4 分别为自适应非奇异终端滑模观测器下得到的仿真结果。
由图4(a)、(b)可以看出,设置电机初始转速为1 000 r/min,在0.02~0.03 s 升高为1 200 r/min,在0.05~0.06 增加载荷10 N/m。可以看出自适应非奇异终端滑模观测器即使是在转速和载荷突变的情况下也能快速准确地跟踪转速实际值,并很好地抑制了抖动现象,转速估计误差在转速突变的情况下也不超过5 r/min,稳态运转时都不超过4 r/min,变化非常小,跟踪精度高。由图4(c)、(d)可以看出,转子位置的最大误差不超过0.8 rad,误差很小。

图4 自适应非奇异终端滑模观测器Fig.4 Adaptive nonsingular terminal sliding mode observer
图5 为自适应非奇异终端滑模观测器下两轴的反电动势估计值曲线。由图可知,得到的反电势波形较平滑,在削弱电压尖峰的同时有效抑制了传统滑模观测器的抖振现象,使转子位置和转速的观测值更准确。
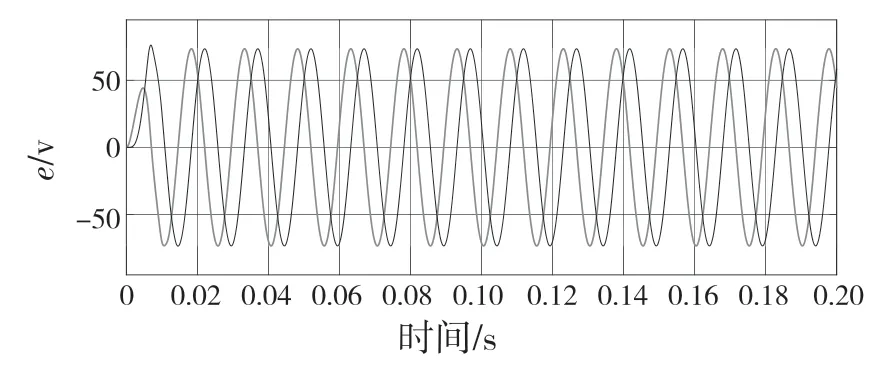
图5 两轴的反电动势估算曲线Fig.5 Estimation curve of extended electromotive on two axes
4 结语
本文在分析研究永磁同步电机无位置传感器矢量控制的原理、传统滑模观测器以及控制算法的基础上,基于非奇异终端滑模控制设计了一种自适应非奇异终端滑模观测器,利用李雅普诺夫函数进行了稳定性和可行性证明,并通过MATLAB/simulink 进行了仿真实验。仿真结果表明,此观测器与传统滑模观测器相比,系统动态响应快、控制精度高,而且系统对负载和各参数的变化具有较强的鲁棒性,稳定性好。
