矩形渠道翼形量水槽的体型优化及试验研究

刘鸿涛，蔡蝶，吴波，赵瑞娟，魏希莹，屈忠义

(1. 内蒙古农业大学水利与土木建筑工程学院，内蒙古 呼和浩特 010018； 2. 长春工程学院水利与环境工程学院，吉林 长春 130012； 3. 吉林省水工程安全与灾害防治工程实验室，吉林 长春 130012； 4. 长春工程学院机电工程学院，吉林 长春 130012； 5. 松辽水利委员会，吉林 长春 130012； 6. 永吉县星星哨水库灌区管理处，吉林 长春 132214)

灌区量水是灌区用水管理重要的基础工作[1-2]. 量水槽是一种利用管道文丘里测流原理，通过在渠道中修建断面缩小的槽形建筑物，形成临界流进行流量测量的量水设施[3].自引用量水槽以来，中国科研人员针对渠道类型，在传统量水槽的基础上进行了深入研究和创新，发明了无喉道量水槽、抛物线形量水槽、机翼形量水槽、圆柱形量水槽等[4-5]新型量水槽.其中由潘志宝等[6]研发的机翼形量水槽，其水头损失小，过流能力强，不易产生淤堵，尤其适用于中国北方含沙量较高的灌区.但机翼形量水槽也存在淹没出流时适用性降低的问题.因此，文中在机翼形量水槽的基础上对量水槽壁面曲线进一步优化，旨在寻求解决淹没出流时，测流精度不满足要求等问题的方法，提高量水槽在平原灌区的适用范围.

1 量水槽体型优化构想

鸟类在上亿年的进化演变中，形成了有利于飞行的独特翅膀结构.有关于仿生翼形的气动性能研究已充分揭示了鸽子高效飞行的原理.由于鸽子高速飞行时的高雷诺数气流流态与过槽水流流态具有相似性，因此文中截取鸽翼主翼段[7]截面曲线作为原型曲线，制作鸽翼形量水槽模型，如图1所示，并在矩形渠道试验平台上进行试验探究.

图1 鸽翼形量水槽实物图

1.1 曲线拟合

由于试验经费有限以及出于对自然界动物的保护，文中通过查阅相关鸽翼气动性能研究的文献[7]，获得鸽翼主翼段截面照片，并将照片导入CAD软件中，进行数字化处理，如图2所示.

图2 鸽翼主翼段截面曲线图

为了使鸽翼主翼段截面曲线能够作为量水槽的壁面曲线进行应用，试验采用水平线截取的方法，获取主翼段截面的上轮廓线，并将点绘得到的上轮廓线坐标数据导入Origin中进行公式拟合.研究发现，虽然阶数越高拟合的曲线精度越好，但曲线公式过于冗长不利于量水槽的工程应用，因此最终采用了能够很好地描绘该曲线特征，且R2大于0.95的5阶多项式进行曲线方程拟合，得式(1)，即

y=0.746 75+0.296 38x+1.214 57×10-5x2-

1.466 7×10-6x3+2.908 83×10-9x4-

3.107 89×10-12x5.

(1)

1.2 结构设计

矩形渠道鸽翼形量水槽由收缩段、喉口、扩散段组成，如图3所示，图中H为量水槽上游稳定断面水深，mm；h为量水槽下游稳定断面水深，mm；BC为喉口宽度，mm；B为渠道宽度，mm；L为翼长，mm;p为翼高，mm.文中研究的鸽翼形量水槽收缩比ε为0.541，翼长L为954.81 mm，翼高p为68.9 mm，喉口宽度BC为162.2 mm.模型试验的渠道长为7 m、渠宽0.3 m、渠深0.4 m，渠道由有机玻璃板连接而成，渠道底坡为平底.

图3 鸽翼型量水槽结构图

量水槽上下游渠道每隔30 cm左右设置1个测量断面，上游断面编号为1—12，下游断面编号为23—32；由于量水槽段水流变化迅速，测量断面间隔过大时，无法精确地描绘流态变化，因此量水槽段每隔10 cm左右设置1个测量断面，编号为13—22,其中断面13为量水槽进口断面，断面22为量水槽出口断面，断面16为量水槽喉口断面.

1.3 测流原理

矩形渠道鸽翼形量水槽，其过水断面沿程为矩形，在收缩段内，水流由缓流变为急流，并在喉口下游某断面形成临界流，对应断面水深称为临界水深.临界流位置的水深与流量存在稳定关系，通过临界流原理[8]推导流量公式的基本形式为

Q=Ghβ,

(2)

式中：Q为流量，L/s；G为流量综合修正系数；β为流量综合指数.

2 试验布置

图4为试验体系示意图.

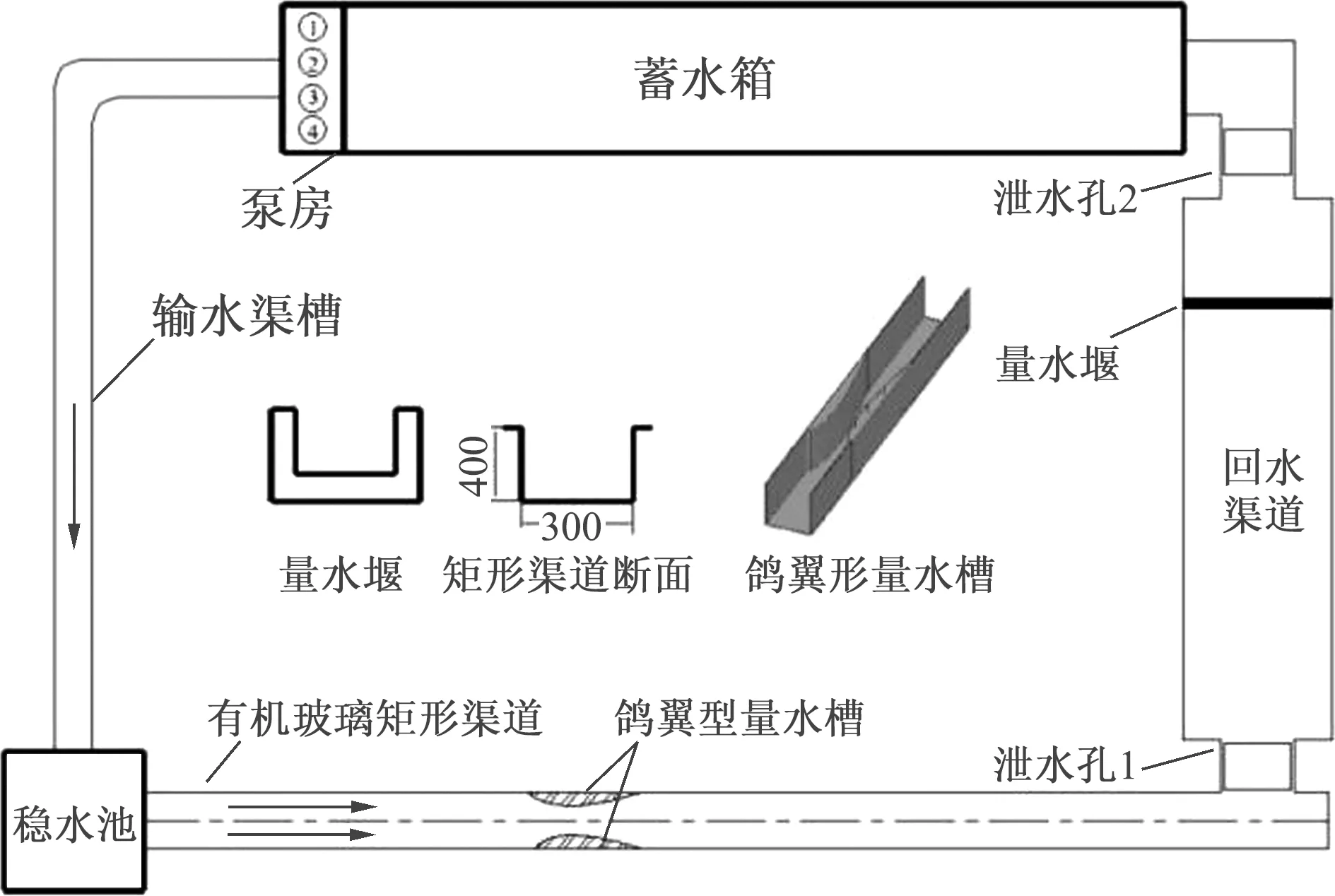
图4 试验体系示意图

试验体系由水泵、蓄水箱、输水管道、稳水池、矩形渠道、鸽翼形曲线量水槽、尾门升降挡板、回流渠道、量水堰、回流管道等组成.由水泵从蓄水箱中抽水，通过输水管道进入稳水池，流入矩形渠道，由泄水孔1下泄到回水渠道，流经量水堰后由泄水孔2回到蓄水箱.试验开始前，采用便捷式声学多普勒超声波流量计(测流精度为0.5 %)对量水堰进行校核，试验量水槽安装于矩形渠道上游稳定水流位置，槽体按顺水流方向沿渠道中轴线安装在渠道两侧边壁，试验体系示意图如图4所示.

在10种流量工况(2.888～18.371 L/s)下，分别对鸽翼形量水槽自由出流和淹没出流进行模型试验.试验通过控制变频水泵机组对流量进行调节，淹没度由尾门升降板进行调节.水位采用SCM 60型水位测针(精度为0.1 mm)测量.

3 翼形曲线量水槽试验结果分析

3.1 水面线

水面线可以直观地反映过槽水流沿程变化情况.图5为鸽翼形量水槽在不同流量Q、不同流态下的水面线，图中L为水深，Di为断面编号，其中i=0—32.

图5 自由出流及淹没出流水面线图

自由出流时，槽前水面线趋于直线，水流平稳；进入量水槽后，水面迅速跌落，在断面16(喉口)附近水面线斜率最大；在断面22(出口)位置，水跃现象随着流量的增大逐渐由弱变强，当流量大于16.192 L/s时不再产生水跃，而是继续出现水跌现象.淹没出流时，渠道水深整体高于自由出流时各断面水深，量水槽内水面以喉口断面为对称轴约呈倒三角形状，这是由于槽前水流通过喉口后流速变大且受扩散段壅水影响，在喉口位置发生淹没式水跃，且这种现象随着流量增大越发明显.

3.2 流量公式

试验通过分析量水槽各断面的水深-流量的相关系数R，确定量水槽的水深-流量控制断面.自由出流时，量水槽内断面水深-流量相关系数R为0.977 8～0.995 0，其中最大值发生在断面14；淹没出流时，量水槽内断面水深-流量相关系数R均在0.850以上，虽然较自由出流时的相关系数有所减小，但依据数理统计的知识，此时的水深-流量也是存在较强相关性的，且相关系数R的最大值也在断面14位置，因此综合考虑，选取断面14作为水深-流量控制断面.

改变流量工况，测量不同流量下断面14的水深数据，拟合流量公式确定综合修正系数G和流量综合指数β；淹没出流时，流量不仅与控制断面水深存在相关性，还与淹没度St有关[9]，因此对于淹没出流的流量公式采用自定义函数的方法进行拟合，确定函数的系数以及幂指数.拟合得到自由出流和淹没出流的流量公式：

1) 自由出流

Q=1.030 3×h1.082 73,R2=0.991 4.

(3)

2) 淹没出流

Q=0.394 5×h1.371 42×St6.509 42,R2=0.887 3.

(4)

3.3 测流精度

图6为计算流量与实际流量对比图，图中Qi为流量工况编号，i为1—10.

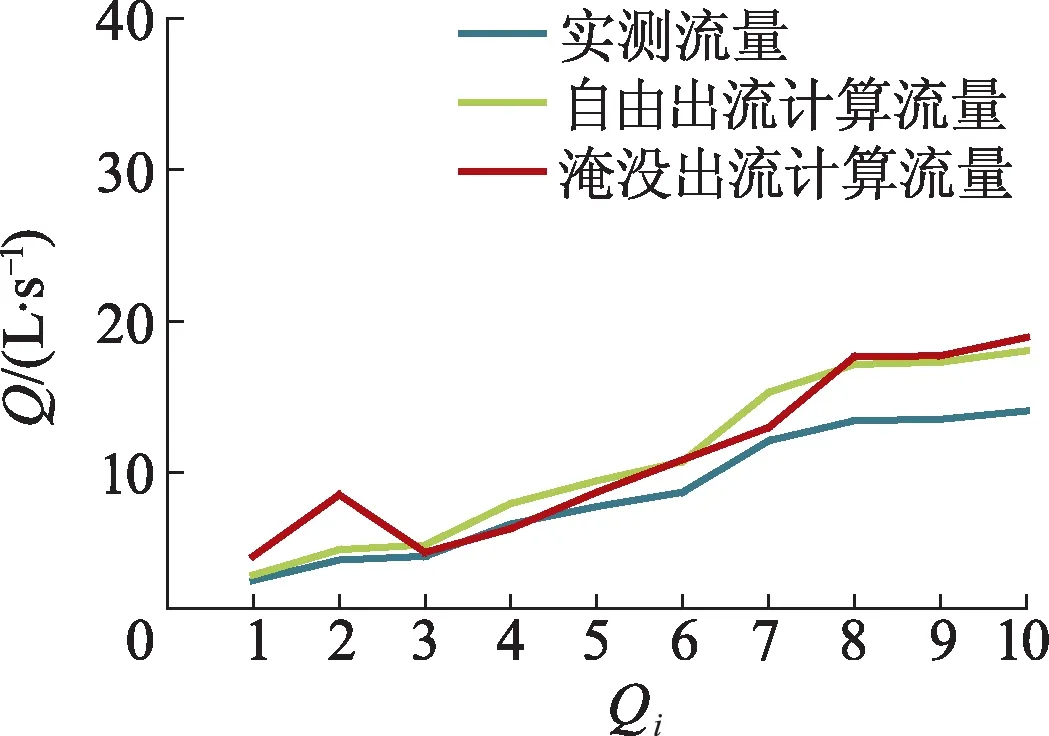
图6 计算流量与实际流量对比图

测流精度是衡量明渠量水建筑物性能优劣的主要技术指标，因此将计算流量和实测流量进行对比，以检验量水槽测流性能的好坏.测流精度计算公式为

(5)

式中：e为测流相对误差；Qc为根据流量公式计算得到的计算流量，m3/s；Qm为试验实测流量，m3/s.

计算得到测流误差结果，如图6所示，自由出流测流误差较小，基本在2%～3%，满足灌区测量规范[10]要求，淹没出流在小流量时误差较大，当流量大于4.377 L/s(工况2)后，测流误差逐渐减小.这是由于随着流量增大，佛汝德数逐渐减小，水流流态逐渐趋于平稳，导致误差越来越小.这与潘志宝[11]在研究U形渠道机翼形量水槽时，发现同一收缩比时佛汝德数随流量增大而减小的结论是一致的.

3.4 佛汝德数Fr

明渠水流具有与大气相接触的自由表面，有独特的水流流态，佛汝德数Fr是明渠水流流态的重要判别数.计算公式为

(6)

式中：v为平稳水流断面平均流速，m/s；g为重力加速度，m/s2.

本试验研究的鸽翼形量水槽沿程佛汝德数Fr，如图7所示.

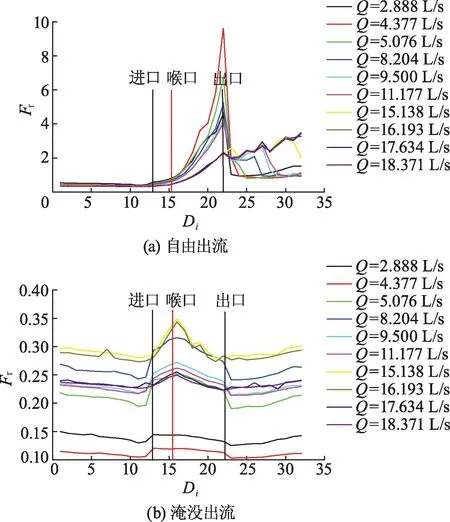
图7 自由出流及淹没出流的沿程佛汝德数

自由出流时，量水槽上游佛汝德数Fr趋于直线且小于0.5，说明此时量水槽上游水流平缓；当进入量水槽后，佛汝德数Fr逐渐增大，水流波动逐渐变得剧烈，在断面16和断面18之间(喉口以下200 mm位置)，佛汝德数Fr等于1，此时对应临界流状态；水流通过喉口后，发生远趋势水跃，水流波动进一步加剧，在断面22(出口断面)Fr达到最大值.

淹没出流时，量水槽的沿程佛汝德数Fr呈现以喉口断面为对称轴的对称趋势，量水槽段佛汝德数Fr先增大后减小，佛汝德数Fr随流量的增大而减小；在10种流量工况下，佛汝德数Fr均小于0.35，即淹没出流时，水流状态较为平稳.

3.5 临界淹没度

临界淹没度是量水槽自由出流变为淹没出流的极限情况.当量水槽的淹没度小于或等于临界淹没度的时候，下游水深对上游水深没有影响，称为自由出流；当量水槽的淹没度大于临界淹没度的时候，下游水深对上游水深产生影响，称为淹没出流.文中计算得不同流量下的临界淹没度Scr，见表1，表中h上为上游水深，h下为下游水深，hcr为影响上游水深时的下游水深.由表1可知，鸽翼形量水槽临界淹没度均在0.850以上，最高可达0.933，且随流量增大而减小，说明鸽翼形量水槽具有较大的测流范围.

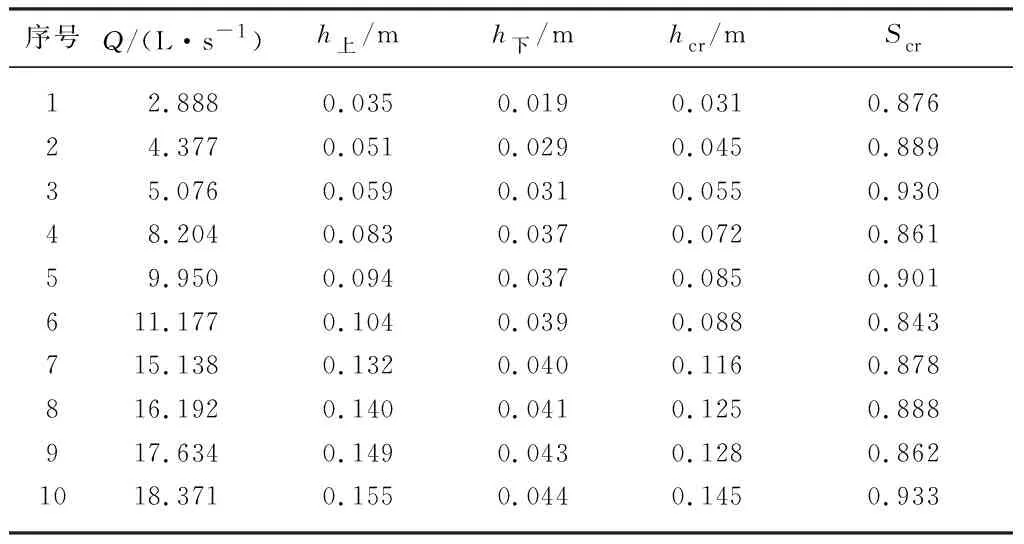
表1 临界淹没度计算表

3.6 鸽翼形量水槽与机翼形量水槽测流性能对比

机翼形量水槽和鸽翼形量水槽在自由出流时测流性能相近，因此基于淹没出流条件，对比二者测流性能.其中矩形渠道机翼形量水槽流量公式已在文献[12]中推导得到.试验结果如图8所示，在10种流量工况下，鸽翼形量水槽的测流误差均小于机翼形量水槽，说明鸽翼形量水槽在保证测流精度的同时，在一定程度上改进了机翼形量水槽在淹没出流时测流精度不高的问题，扩大了量水槽在平原灌区的适用范围.

4 结 论

1) 从水面线方面，不同流态水跃发生位置不同.自由出流时，鸽翼形量水槽的水跃发生在出口断面附近，淹没出流时，该现象发生在喉口附近.

2) 从测流精度方面，不同流态测流精度不同.自由出流时的测流精度整体高于淹没出流，测流误差为2%～3%，淹没出流在小流量时误差较大，当流量大于4.377 L/s后，测流误差逐渐减小，说明鸽翼形量水槽在淹没出流状态下也可以正常工作.

3) 从佛汝德数方面，不同流态水流剧烈波动位置不同.水流波动剧烈位置与结论1中水跃位置相同，符合能量守恒理论.

4) 从临界淹没度方面，鸽翼形量水槽的临界淹没度随流量增大而增大，且最高可达0.933，说明该量水槽在测量大流量工况时存在较大的自由出流空间，同时在淹没出流时又能保证一定的测流精度，因此整体上扩大了该量水槽的适用范围.为解决量水槽在平原灌区应用受限的问题提供了一定帮助.