基于IMM的机动目标卡尔曼跟踪滤波算法

李越强

(解放军91977部队，北京 100036)

0 引 言

机动目标跟踪问题一直是人们研究的重点，为了实现机动目标高精度稳定跟踪，首先要建立与实际目标运动相匹配的目标运动模型[1-2]。而常规跟踪滤波算法对目标跟踪时基于某一种运动模型，因此难以适应机动目标随时改变运动状态，针对机动目标跟踪，目前常用的有多模型、交互式多模型(IMM)、切换模型等方法[3-4]。多模型方法就是对一组不同机动模型分别进行跟踪滤波，最终的参数估计是各滤波器估计值的加权和。在多模型基础上，Bar-Shalom提出了交互式多模型方法，这一方法对无序目标的机动检测显示了更好的鲁棒性和跟踪的稳定性。切换模型则是分别建立机动和非机动运动模型，利用机动检测实现在这2个模型之间的切换[5-7]。一般来说，IMM的跟踪性能较好。

本文对二维空中机动目标进行了研究，首先对机动目标跟踪原理、Kalman滤波算法以及IMM方法原理进行了阐述，并采用Kalman滤波算法对基于单模型和IMM机动目标跟踪进行了仿真比较分析。

1 机动目标跟踪原理

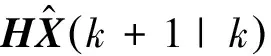
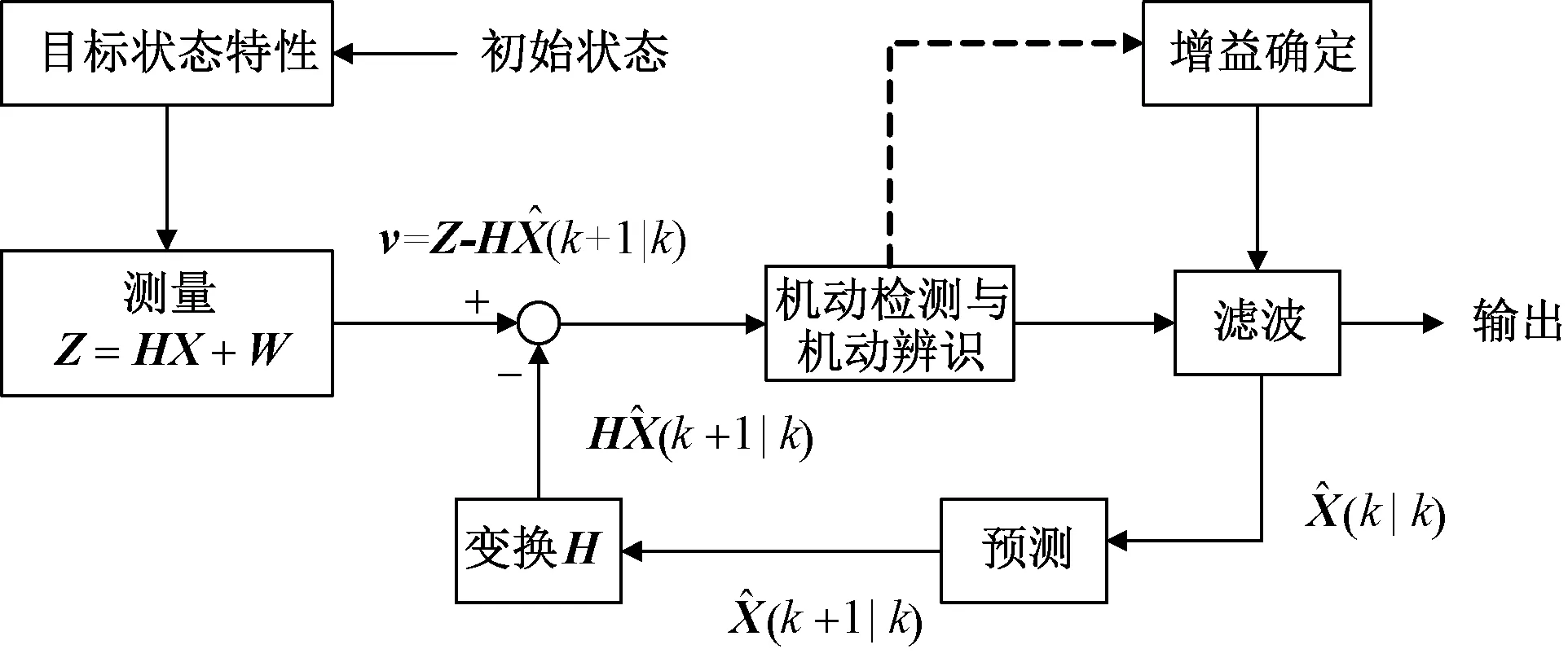
图1 机动目标跟踪基本原理图

2 机动目标跟踪算法

2.1 卡尔曼滤波算法

卡尔曼滤波器目标基本运动模型：

X(k+1)=Φ(k+1,k)X(k)+Γ(k)W(k)

(1)

式中：X(k)为当前k时刻目标运动状态向量；Φ(k+1,k)为目标状态从k时刻到k+1时刻的状态转移矩阵；Γ(k)为系统模型噪声系数矩阵。

基于式(1)模型目标观测方程，有：

Z(k+1)=C(k+1)X(k+1)+V(k)

(2)

式中：W(k)为模型量测噪声协方差矩阵；W(k)、V(k)为均值、高斯随机序列。

卡尔曼滤波算法基本步骤如下：

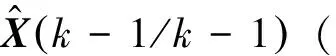
(3)

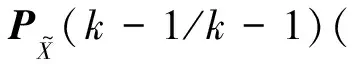
ΦT(k,k-1)+Γ(k-1)Q(k-1)ΓT(k-1)

(4)

(3) 当前k时刻卡尔曼增益计算：

(5)

(4) 计算当前k时刻滤波估计:

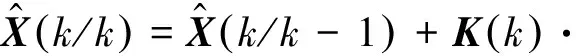
(6)

(5) 计算当前k时刻滤波误差方差阵:

(7)

卡尔曼滤波算法计算滤波估计及滤波增益和协方差矩阵计算流程图如图2、图3所示。

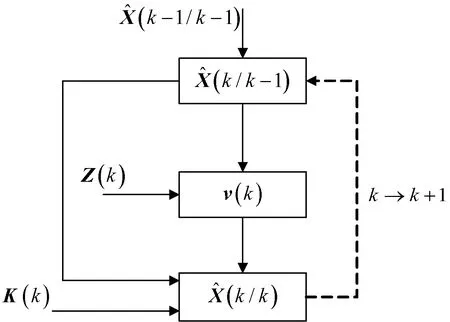
图2 计算滤波估计流程图

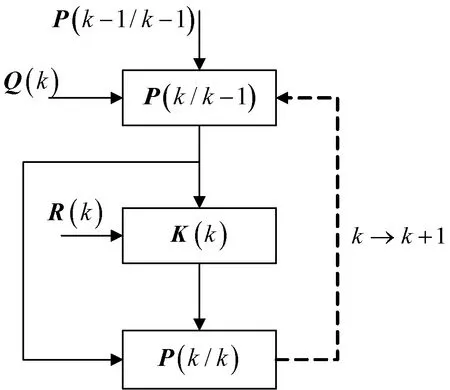
图3 卡尔曼滤波增益和误差方差阵计算流程图

在应用卡尔曼滤波算法时，需要指定滤波器起始条件，可根据目标的初始状态计算出卡尔曼滤波器起始条件。起始条件的建立参考文献[3]中有详细描述，在此不再赘述。

2.2 交互多模型方法

IMM方法中，每一个运动模型对应着相应的滤波器，具备多个滤波器、1个模型概率估计器、1个交互式作用器和1个估计混合器，通过多个模型相互作用跟踪1个机动目标，具有r个模型的IMM方法原理框图如图4所示。

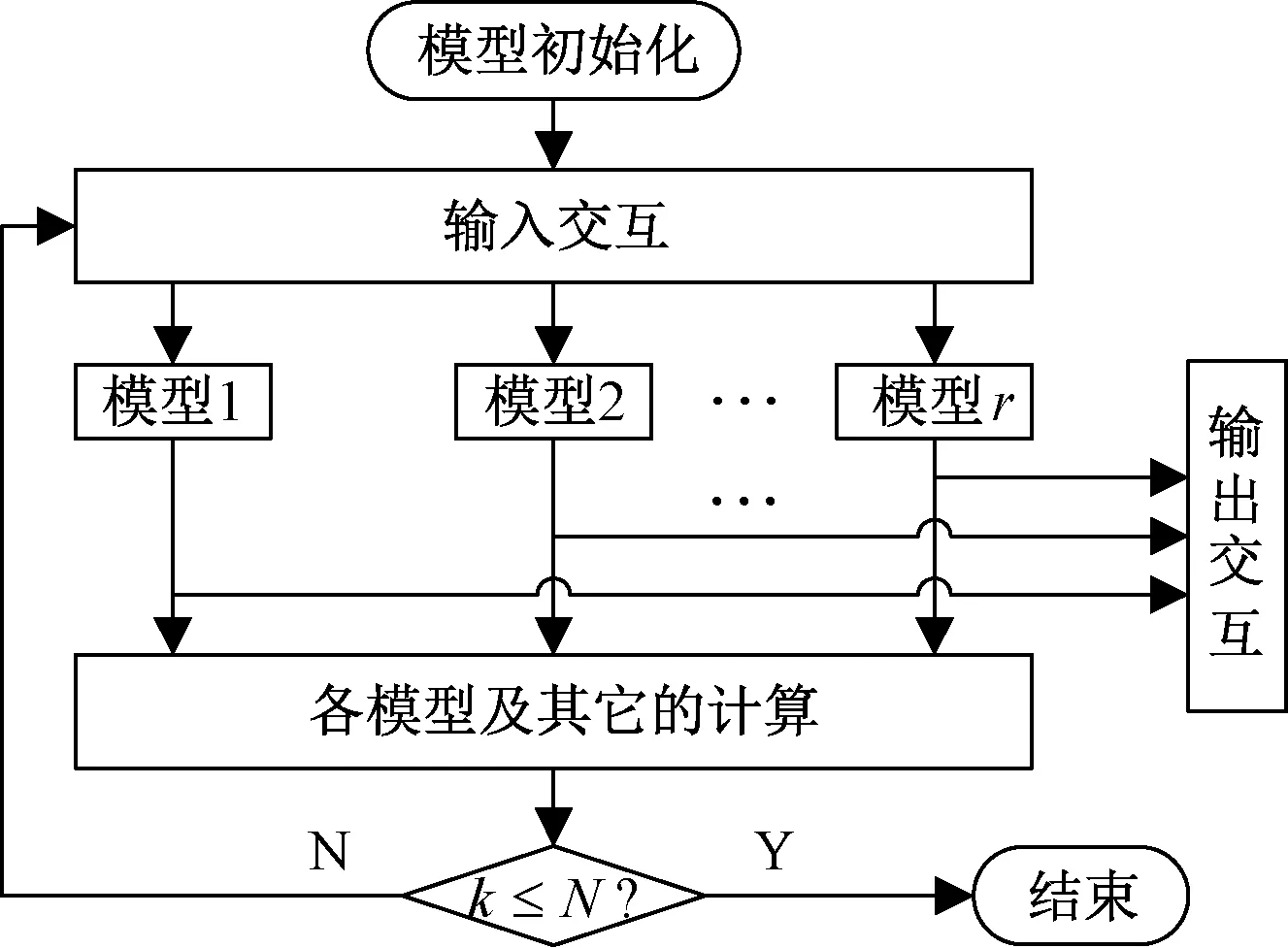
图4 IMM方法原理框图

假设IMM方法中各模型间切换概率是基于马尔科夫链计算的，那么各个模型交互作用器利用模型概率和模型转移概率类计算每一个滤波器的交互作用。从模型i转移的模型j的转移概率为pij，马尔科夫链转移概率矩阵如下：

(8)

IMM方法滤波循环开始后，每一个滤波器利用多个模型交互式估计和测量数据计算出一个新的估计和模型的可能概率，然后，前一时刻的模型概率、模型可能性、模型转移概率被用来计算新的模型概率，那么总的状态就可以通过新的状态估计以及相应的模型概率计算出来。

基于马尔科夫链的交互多目标概率切换计算的IMM方法步骤如下：

(1) 输入交互：

(9)

其中：

(10)

Poj(k-1/k-1)=

(11)

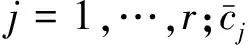
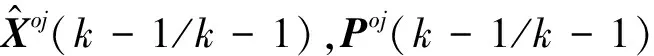
(3) 模型概率更新计算

若第k时刻，模型Mj(k)的滤波残差为υj(k)，相应的协方差为Sj(k)，假设服从高斯分布，则模型Mj(k)的可能性为：

Λj(k)=P{Z(k)/Mj(k),Zk-1}=

(12)

其中：

(13)

模型Mj(k)的概率更新为：

(14)

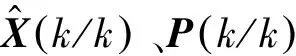
(15)

(16)

3 仿真分析

采用卡尔曼滤波算法对基于单模型和IMM机动目标跟踪滤波仿真，IMM包含3种模型：模型1为匀速直线运动模型，模型2为右转机动模型，模型3为左转机动模型。分别利用IMM和以上3种单个模型对机动目标进行跟踪。3种模型状态转移矩阵分别为：

(17)

(18)

(19)

式中：T目标采用时间间隔，取值1 s；ω为目标转弯角速率，取值3°/s。

图5 目标运动轨迹

分别采用IMM方法以及3种单模型(匀速直线、左转、右转)的Kalman滤波对该机动目标进行跟踪，其滤波后轨迹、IMM方法模型概率曲线、不同模型滤波的x/y坐标位置误差以及不同模型滤波的x/y方向速度误差分别如图6～图11所示。

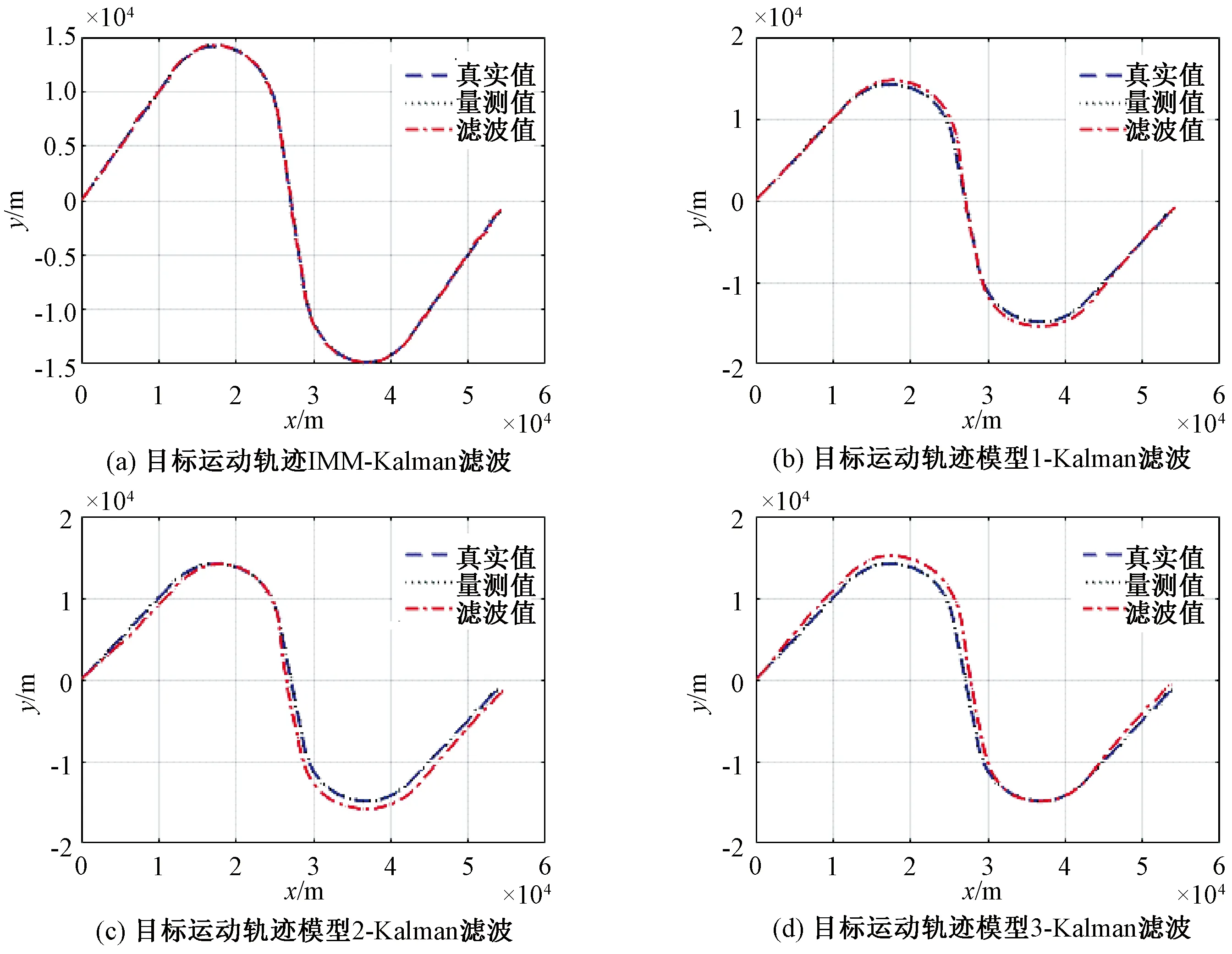
图6 基于IMM、模型1、模型2以及模型3四种Kalman滤波轨迹结果

通过图6、图8、图9、图10和图11可以看出，采用模型1对机动目标进行跟踪滤波时，与模型1相匹配的第1、3、5段轨迹的位置和速度跟踪误差相对于其他模型更小，滤波后轨迹在第1、3、5段更接近真实轨迹；由于其他轨迹段与模型1不匹配，在其他轨迹段出现了较大的位置和速度跟踪误差，其他轨迹段滤波后轨迹较真实轨迹有较大偏差。

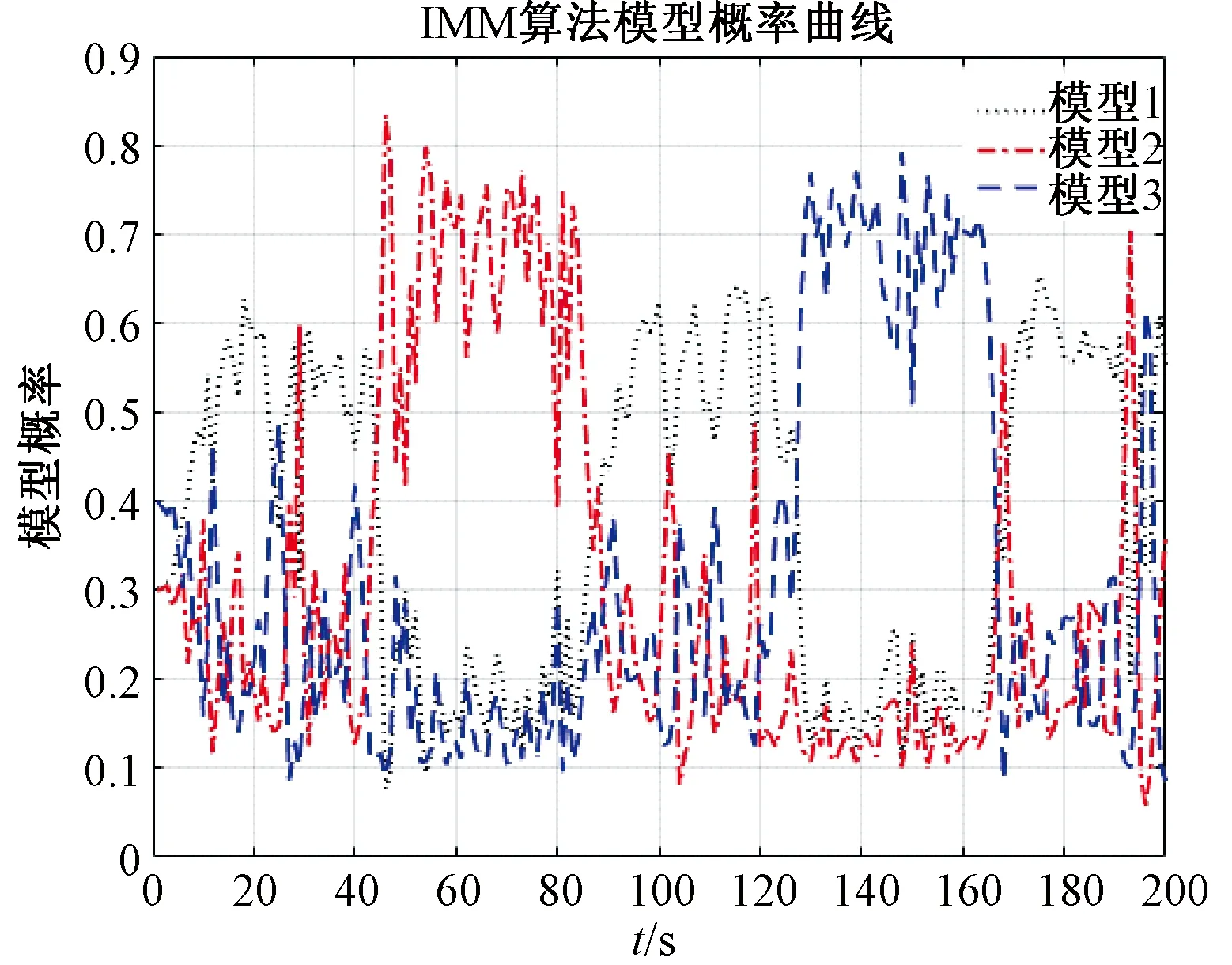
图7 基于IMM方法滤波模型概率曲线

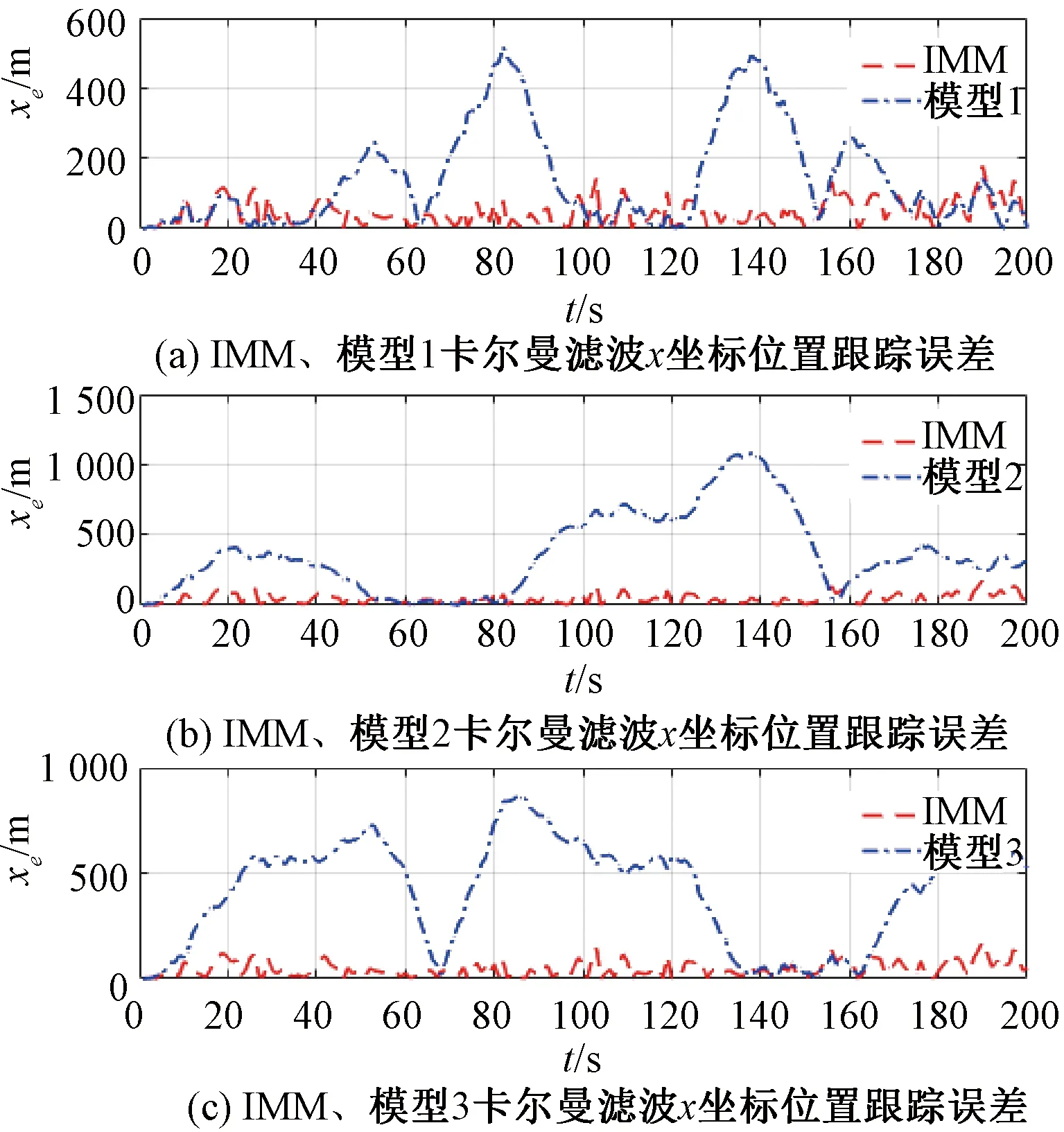
图8 IMM与单模型滤波x位置跟踪误差比较

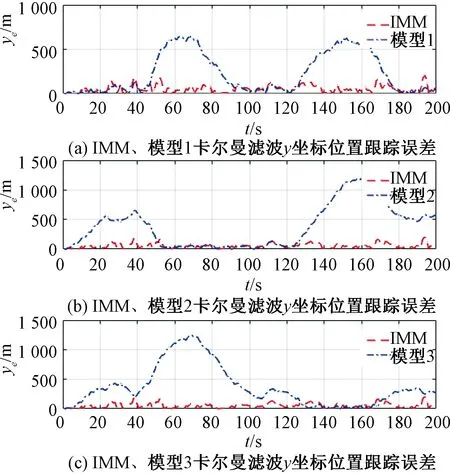
图9 IMM与单模型滤波y位置跟踪误差比较

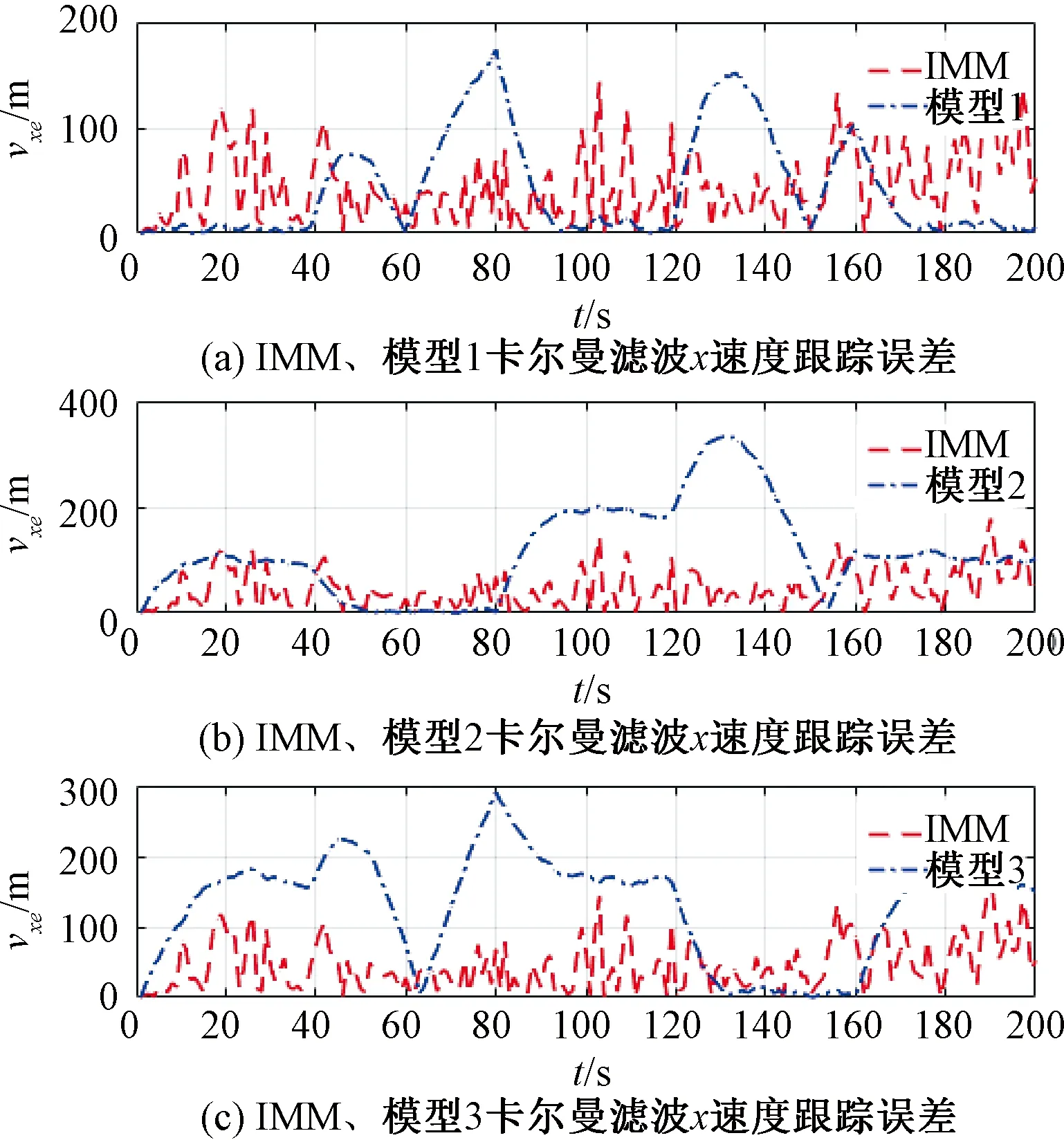
图10 IMM与单模型滤波x速度跟踪误差比较

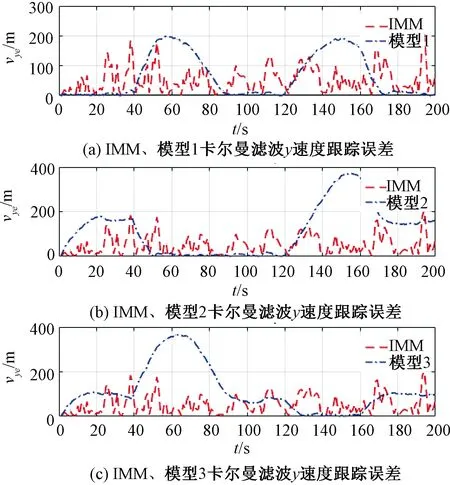
图11 IMM与单模型滤波y速度跟踪误差比较

采用模型2对机动目标进行跟踪滤波时，与模型2相匹配的第2段轨迹的位置和速度跟踪误差相对于其他模型更小，滤波后轨迹在第2段更接近真实轨迹；由于其他轨迹段与模型2不匹配，在其他轨迹段出现了较大的位置和速度跟踪误差，其他轨迹段滤波后轨迹较真实轨迹有较大偏差。

采用模型3对机动目标进行跟踪滤波时，与模型3相匹配的第4段轨迹的位置和速度跟踪误差相对于其他模型更小，滤波后轨迹在第4段更接近真实轨迹；由于其他轨迹段与模型3不匹配，在其他轨迹段出现了较大的位置和速度跟踪误差，其他轨迹段滤波后轨迹较真实轨迹有较大偏差。

采用IMM方法对机动目标进行跟踪滤波时，由图7可知，在各段轨迹中，第1、3、5段轨迹与模型1更匹配，在该3段轨迹中模型1的概率比其他模型更高；第2段轨迹与模型2更匹配，在该段轨迹中模型2的概率比其他模型更高；第4段轨迹与模型3更匹配，在该段轨迹中模型3的概率比其他模型更高。IMM滤波预测输出结果由各模型滤波结果加权输出，但主要由匹配度较高的模型滤波结果确定。

图12为采用该算法对无人机跟飞实测数据，图13和图14分别为无人机X和Y方向的运动状态和跟踪误差。从实际数据可以看出该算法在无人机机动时，能很好地跟踪目标，且在进入稳定航迹后，跟踪误差逐渐收敛，具有良好的跟踪效果。

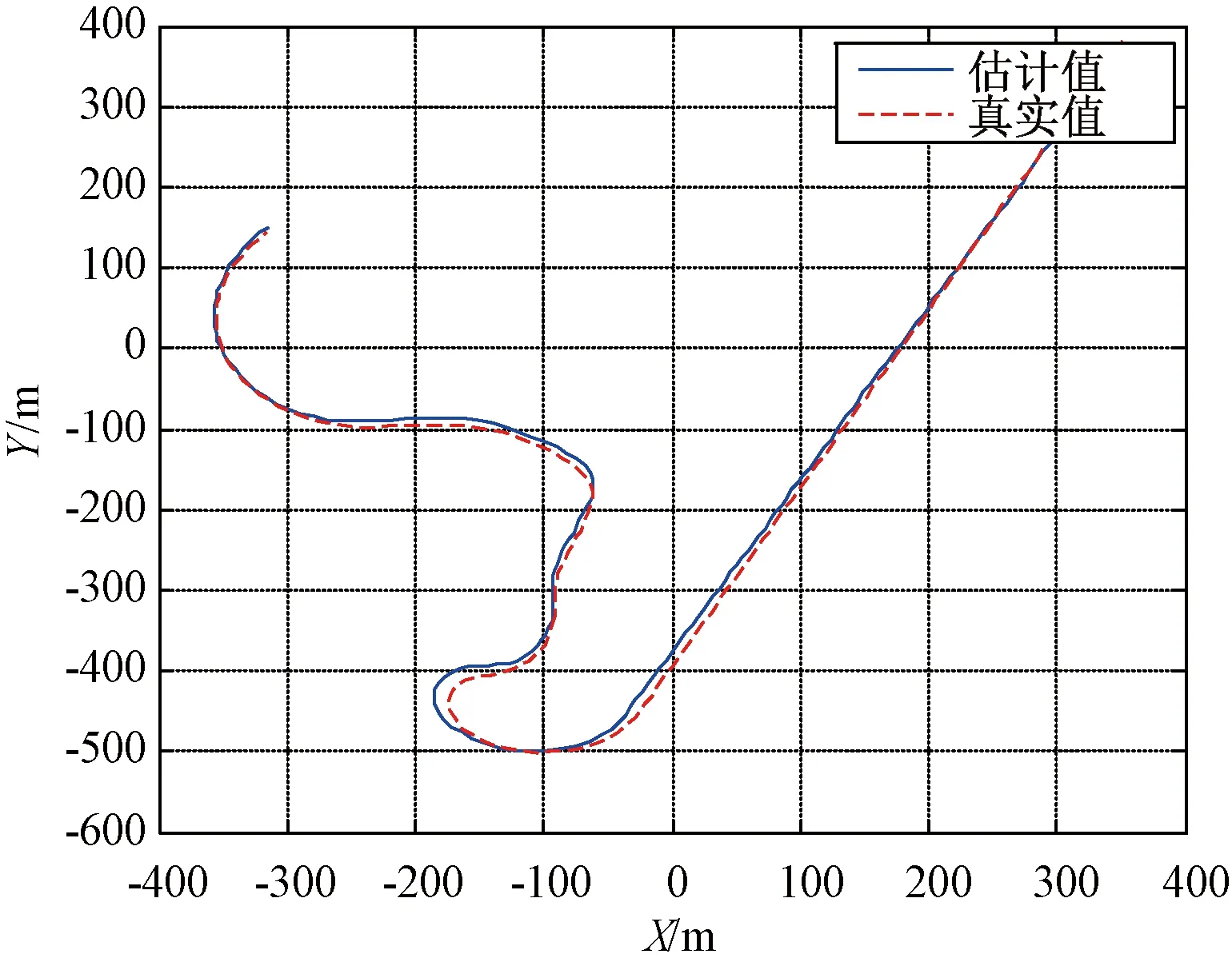
图12 无人机运动轨迹

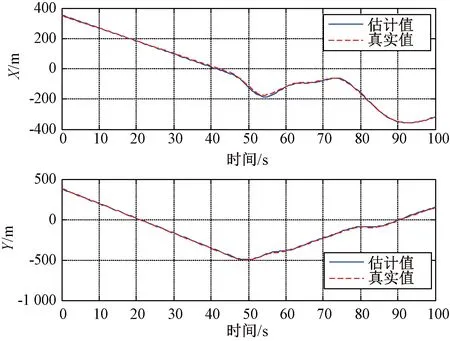
图13 无人机各方向运动状态

图14 无人机各方向滤波跟踪误差

在目标进行机动时，基于IMM跟踪滤波可实时更新计算各模型概率。与当前轨迹匹配最高的模型概率更大，IMM跟踪滤波结果受匹配度更高模型的滤波影响也就更大，使得目标机动全程均能很好地对其跟踪滤波，相较于采用单模型对机动目标跟踪滤波，具有更高的滤波精度。但由于IMM方法包含多种模型，跟踪滤波时，多种模型同时跟踪滤波，且还需更新计算模型概率以及交互计算等，相较于单模型跟踪滤波，计算量更大，对硬件要求更高。

4 结束语

本文主要对基于IMM机动目标卡尔曼跟踪滤波算法进行阐述，IMM机动目标跟踪能够实时选择与当前目标运动匹配度最高的模型滤波主导IMM输出结果，相较于单模型仅能对机动目标中与该模型相匹配的一段运动轨迹进行高精度跟踪，IMM能够实现机动目标全程较高精度稳定跟踪。理论上只要IMM包含的模型种类足够多，且机动目标各阶段总能与IMM中某一种模型相匹配，IMM就能实现对机动目标高精度全程稳定的跟踪，但考虑到IMM的计算量以及实际机动目标运动模型，IMM一般包含几种典型运动模型以及适合的模型参数库就能很好地对机动目标进行跟踪。