基于多源数据集成的地理信息系统数据高效整合研究

刘 波

（山东省国土测绘院，山东 济南 250013）

0.引言

在信息技术飞速发展的背景下，地理信息系统的设计研发取得了质的飞跃[1]。随着地理信息指标不断地细化，地理信息系统产生了海量的数据，如何在分析工作过程中迅速整合数据成为了当下的研究热点[2]。从地理数据的整合本质来看，数据整合过程就是将地理信息系统中的数据处理为多源数据集后，利用数据集内数据的多源性以及多尺度性，设定数据管理标准，将不同管理项目内的数据整合为相同的量纲的过程[3]。在该种数据整合方法的支持下，不同类型的地理信息系统数据之间能够形成协调一致的状态，为高效分享地理信息数据提供支持。由此可知，研究基于多源数据集成的地理信息系统数据高效整合方法具有必要性。

在上世纪五十年代中期，国外研究人员将集成管理技术与地理空间处理技术作为技术支持，设定了数据整合的统一标准[4]，实现了不同系统间的数据跨平台互通。国内地理信息系统研究起步较晚，研究人员归纳总结了地理信息系统数据的特点，确定了数据整合工作首要解决的问题，并构建了数据尺度变换算法。文献[5]中的数据整合方法，以BIM和GIS作为数据集成处理工具，制定了数据整合的数据标准，在三维可视化平台的支持下构建了数据整合过程。文献[6]中的数据整合方法应用Spark环境作为数据处理工具，采样计算信息数据的综合权重，采用基于相关性的特征处理方法构建数据整合规范，构建形成数据整合过程。经阶段性的应用探析可发现，现有的数据整合方法存在整合时间较长、属性匹配度较低的问题，由此可知，研究基于多源数据集成的地理信息系统高效整合过程具有一定的意义。

1.基于多源数据集成的地理信息系统数据高效整合研究

1.1 集成地理信息系统多源数据

地理信息系统内存在多源结构的信息数据，在集成处理时，采用模式树的方法将信息数据处理为层次结构，处理过程如公式（1）所示：

式（1）中，H为构建的层次处理参数；D0为模式树的节点参数；T为数据的处理周期。将模式树结构内的数值按照从大到小的顺序排列，将层次参数大的信息数据划分在模式树内的主节点处，将数值大小相差不大的数据放置在相同等级内的树状节点内，整理为以数值为模式结构点的模式树后，在相同结构内标定信息多源数据的属性，采用节点传递函数处理相同模式树结构内的数据，处理过程如公式（2）所示：

式（2）中，h（v）为构建的节点函数；v为属性参数；W为标定函数；其余参数含义不变。将模式树间的地理信息数据构建数值关系后，为了消除地理信息数据之间的约束，在多源数据内设定一个数值等价条件。设定的等价条件如公式（3）所示：

式（3）中，R为地理信息数据的转换参数；S为信息数据的多源等价参数；G为多源数据的属性参数；其余参数含义不变。等价处理后的多源数据存在一定的异构冲突，为了消除实际产生的异构冲突，采用K关联的处理方式集成多源数据为模式树的结构增量。处理过程如公式（4）所示：

式（4）中，f（i）为构建的模式树节点的增量函数；Bi为多源数据的冲突修正；N为模式树结构内存在的节点总数。此时，在集成处理多源数据过程中，模式树结构内形成了集成传递过程（如图1所示）：

图1 多源数据的集成传递过程

由图1中的集成传递过程可知，在不同结构增量参数的控制下，地理信息系统中的数据处理多个传递条件的多源数据集，利用集成处理后的信息数据集，匹配地理信息数据的属性。

1.2 匹配地理信息数据属性

使用上述集成处理后的多源数据，将模式树结构内的数据处理为属性元素，引用相似度计算公式计算属性元素之间的相似性，计算公式如公式（5）所示：

式（5）中，A、B分别为选定的属性元素；wi为属性元素的相似性权重；J为元素匹配参数。考虑到模式树结构中深层次元素的单位不可分性，在模式树内构建一个路径匹配过程。构建的匹配过程如公式（6）所示：

式（6）中，P为构建路径匹配函数；a为路径条件参数；k为匹配路径的权重因子；d1为元素节点在模式树中的路径距离；其余参数含义不变。将符合路径匹配数值关系的多源数据处理为相同的类别，采用数值扩充的方式重新计算相同路径内的元素相似性，数值关系如公式7所示：

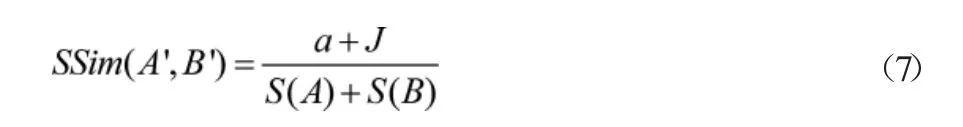
式（7）中，SSim（A′，B′）为相同路径内元素的相似度；S（A）、S（B）分别为相同路径内元素的属性值。将上述处理的相似性数值处理为值域，并以该值域作为匹配过程中的数值条件，最终构建的数据属性匹配过程如公式（8）所示：

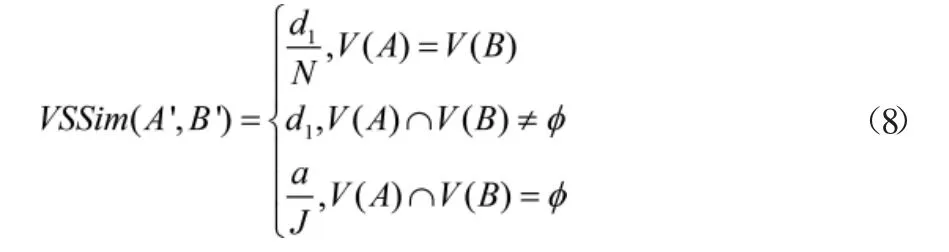
式（8）数值关系中，V为构建的匹配函数；V（A）、V（B）分别表示属性参数形成的数值条件集；其余参数均保持原含义不变。利用上述构建的信息数据属性匹配的数值关系，为了高效实现数据整合过程，构建数据整合算法。

1.3 建立数据整合算法

在上述构建的属性匹配过程中，调用属性匹配形成的数据个体选择过程，根据多源数据之间的个体作用，确定多源数据间数值作用规则，数值关系如公式（9）所示：

式（9）中，Q为设定的数据作用参数；f（A′）、f（B′）为数据匹配属性的相互函数；K为数据匹配次数。为了满足数据整合过程的时效性，在上述的数值作用规则内，采用Metropolis准则设置属性数据更新过程。设定的更新过程如公式（10）所示：

式（10）中，Fi为设定的更新函数；λi为引用准则内的规则函数；ti为设定的更新周期；其余参数保持其原有含义不变。受到地理信息系统数据标度单位的影响，不同地理信息尺度数据在整合时，容易出现数据不兼容的现象。为了处理该现象，在上述构建的数值更新过程内，以设定的更新周期作为自变量，整理更新过程产生的数值阶跃响应（如图2所示）：

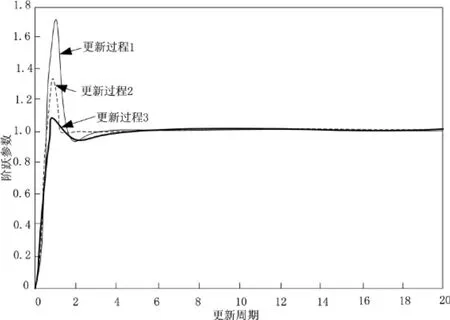
图2 更新过程产生的阶跃响应

由图2可知：在前两个更新周期内，更新数值内产生了数值较大的阶跃，将该阶跃状态下的更新参数作为整合算法内的精细参数，最终构建形成的数据整合算法如公式（11）所示：

式（11）中，D（v）为构建的数据整合算法；L为算法的收敛参数；其余参数保持原有含义不变。为了增强数据整合算法的时效性，转换融合数据的状态为遍历状态，增强数据融合算法的时效性。综合上述处理过程，最终完成对基于多源数据集成的地理信息系统数据高效整合过程的研究。

2.仿真实验

2.1 采集地理信息系统数据

随机调用某地的地理信息系统，调配后台数据中的栅格配准功能，采集得到地理信息系统中的数据，采集过程（如图3所示）：

图3 采集地理信息系统数据过程

数据采集后，将得到的系统数据整理为（如表1所示）的系统数据集：

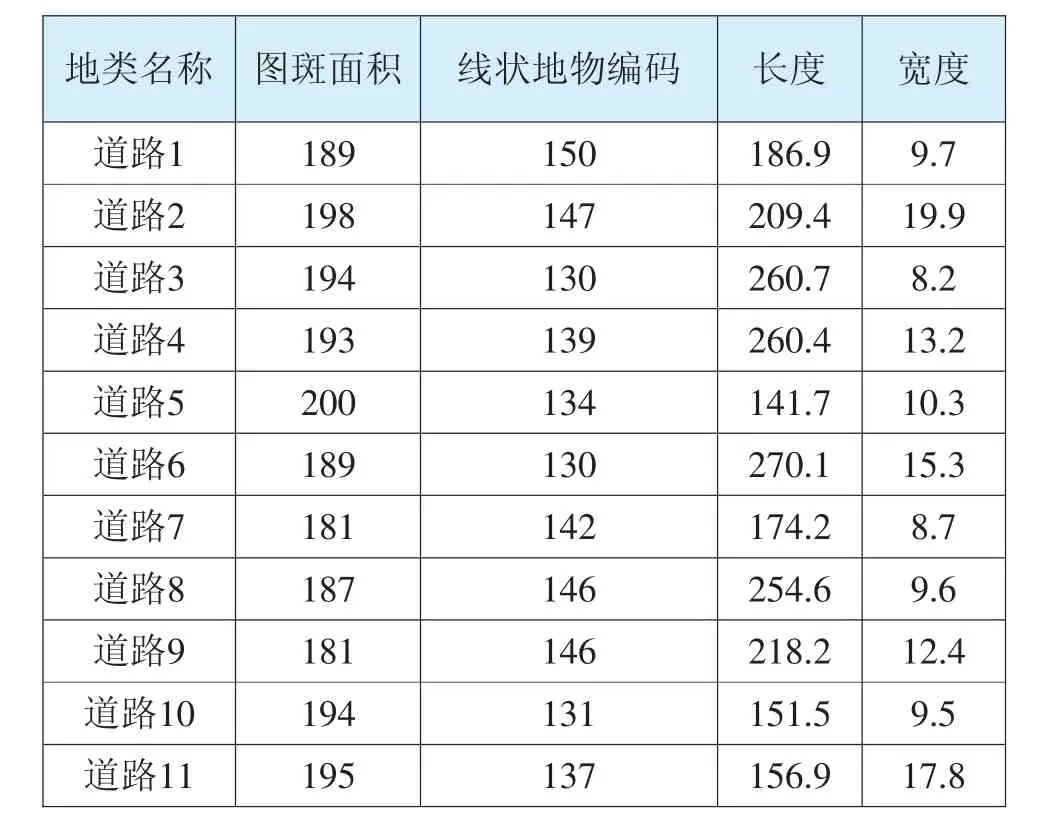
表1 整理得到的地理信息系统数据

在图3所示的系统数据支持下，采用单独图层处理的方式将表1中的数据增量处理为图斑范围，不断核实图斑范围中产生的偏差。，修正处理完毕后，将更新后的信息系统数据作为整合处理对象，应用基于多源异构的整合方法、基于模式映射的整合方法以及所设计的数据整合方法进行实验，选定相同的性能指标作为处理对象，对比三种整合方法的性能。

2.2 结果及分析

使用上述采集得到的地理信息系统数据，对应不同的地类名称，采用XML文档将其映射处理为图斑数据模式。映射处理过程如公式（12）所示：

式（12）中，r（u）为构建的映射模式函数；Ne为参与整合数据的数量；pu为映射的调优参数。将其映射处理为地理图斑数据模式后，以该模式作为地理信息系统的属性，定义三种数据整合方法数据匹配属性的过程，统一计算三种数据整合方法在匹配过程中形成的匹配度，数值关系如公式（13）所示：

式（13）中，α为计算的匹配度；em为数据整合方法内的匹配函数；其余参数含义不变。结合上述构建的匹配度数值关系，在表中地类数据的支持下，整理数据整合方法数据属性的匹配度，结果（如图4所示）：

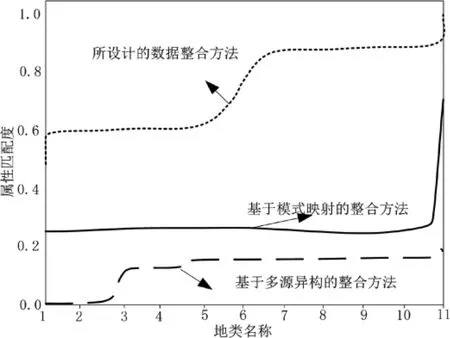
图4 三种数据整合方法属性匹配度结果

在定义采集地理信息数据的图斑属性后，根据映射处理形成的数值关系，构建数据整合方法的匹配度数值关系，定义计算得到的匹配度参数越大，则表明该种数据整合方法匹配地理图斑属性越准确。由图4所示的属性匹配度可知，基于模式映射的整合方法在处理前十种地类时，计算得到的匹配度在0.25左右，在处理第十一种地类时，属性匹配度上升至0.6，该种数据整合方法能够匹配准确的图斑属性，但匹配过程不稳定。基于多源异构的数据整合方法在前五组地类数据内属性匹配呈现了数值突变，在处理剩余地类数据时，匹配度数值保持在0.1左右，该种数据整合方法实际匹配土地图斑属性表现出的准确性较差。而所设计的数据整合方法在处理前五组地类数据时，图斑匹配度数值为0.6，在处理接下来的图像时，匹配度数值上升至0.9，与选定对比的两种数据整合方法相比，所设计的整合方法匹配地理图斑属性最准确。

在上述实验环境下，整理不同地类数据形成的数据量大小，并结合表中各项参数的数值大小，构建数据量数值关系，如公式（14）所示：

式（14）中，c为构建的数据量处理函数；b为线状地编物；L为地理面积的长度；H为地理面积的宽度；S为地理处理面积。对应上述数据量数值关系，处理表中地理信息为数据量，并以该数据量作为自变量，调用运行地理信息系统的上位机，整理三种数据整合方法产生的整合时间，时间结果（如图5所示）：

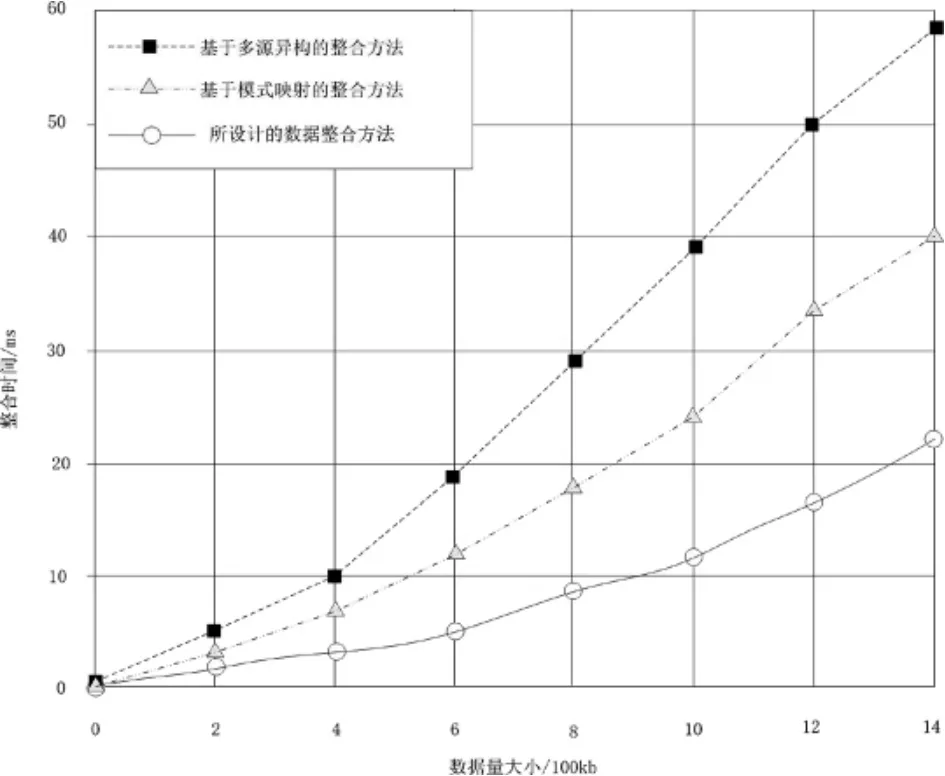
图5 三种数据整合方法所需的时间

在构建的数据量转化公式内，整理上表中的各项数据处理为数据量为0～1400kb的数据，调用运行整合方法的上位机，根据统计得到的时间结果可知，将数据整合方法处理的数据量规范在相同的数值区间时，以1400kb的地理信息数据作为对比指标，基于多源异构的整合方法所需的运行时间为58ms，实际所需的数据整合时间最长。基于模式映射的数据整合方法在相同数据处理量下所需的整合时间为40ms，实际所需的整合时间较长。而所设计的数据整合方法在相同的数据整合量下所需的数据整合时间为22ms，与两种应用对比的数据整合方法相比，所设计的数据整合方法消耗的整合时间最短，时效性最佳。

保持上述实验环境不变，对应上述定义得到的地理图斑属性，对应不同的地类，将采集得到的地理信息系统数据反向验证地理信息系统所构建的图斑面积，调用三种数据整合方法中的处理算法，构建地理面积误差判断数值关系，如公式（15）所示：

式（15）中，V为计算得到的误差；M、N分别为地理图斑的边长；P（ci，αj）为信息数据被整合的概率；i、j分别为信息系统的模式参数；其余参数含义不变。对应上述构建的整合地理图斑面积产生的误差判别数值关系，整理三种数值整合方法产生的误差结果（如图6所示）：

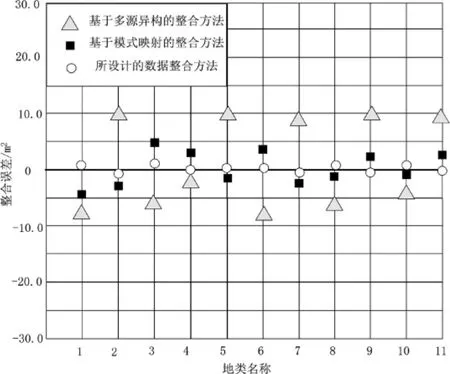
图6 三种数据整合方法整合图斑地理面积产生的误差

根据定义的面积误差数值关系，对应整理三种整合方法整合地理图斑面积产生的误差，由上图可知，定义统计坐标范围内的正向为大于标准地理图斑面积，负向则为小于标准地理图斑面积。结合上述标定的数据点可知，基于多源异构的数据整合方法在设定的地类范围内，实际产生的整合面积误差最大，远远偏离标准地理面积。基于模式映射的数据得到的整合面积误差较小。而所设计的数据整合方法最终实际产生的整合误差点在设定的0线左右，与两种选定的数据整合方法相比，所设计的数据整合方法整合地理图斑面积产生的误差最小。

3.结束语

利用多源数据集成技术作为支持，研究构建了地理信息系统数据整合过程，经实验验证可知，所设计的数据整合过程能够改善现有数据整合方法数据整合时产生的误差过大的问题。在未来工作当中，希望所设计的数据整合过程能够为其提供理论支持。