基于视觉图像的多自由度工业机器人轨迹控制方法
2021-12-27谢梅玲
杨 晶,谢梅玲
(1.广东省广州应用科技学院,广州 511370;2.广东省广州应用科技学院,广州 511370)
0 引言
科技发展带动工业机器人研究领域迅速扩大,为现代机械制造等领域提供越来越精细化、智能化的应用工具,从某种意义上来讲,现代工业机器人已经成为衡量国家科技水平的一项重要工具。随着工业时代的到来,工业机器人产业发展已经取得了重大成就,根据现阶段的工业机器人销量统计数据,可知目前的快递行业、机械制造行业等,都在加大工业机器人的投入使用力度。机器人作为一个多输入、多输出的复杂工具,在使用过程中存在较大的不确定因素,从而影响机器人的运动姿态或移动轨迹,所以近年来多自由度机器人被广泛研究。但根据实际使用现状发现,多自由度工业机器人的运动姿态更加灵活,对于运动、姿态、位置等方面的控制越来越困难,当运动范围有限、目标物位置角度复杂多样的条件下,机器人的轨迹控制效果不佳[1]。针对此类问题基于视觉图像,研究全新的多自由度工业机器人轨迹控制方法。
1 基于视觉图像的多自由度工业机器人轨迹控制方法
1.1 双目立体视觉原理标定活动范围
想要控制多自由度工业机器人的轨迹精度,此次研究依据双目立体视觉原理设计全新的控制方案。已知目标物体的形状、大小等数据,都是通过两只眼睛同时观察得到的,所以双目视觉更接近人眼视觉,利用眼睛将原本二维空间内的信息转换成三维数据,根据视觉图像中的数据获得机器人可活动的范围。根据双目视觉原理的基本内容,将三维空间中存在的随机目标物体,看作一个实心圆点,利用两台摄像机同时观察该点,当确定两个相机的显示图像与该点对应,那么能够确定空间点的信息,得到该点的世界坐标系。但常规情况下的运动为平行运动,假设两个相机完全相同且与x轴重合、与y轴和z轴平行,此时的相机沿x轴方向运动距离d后与另外一个相机的位置重合,如图1所示。
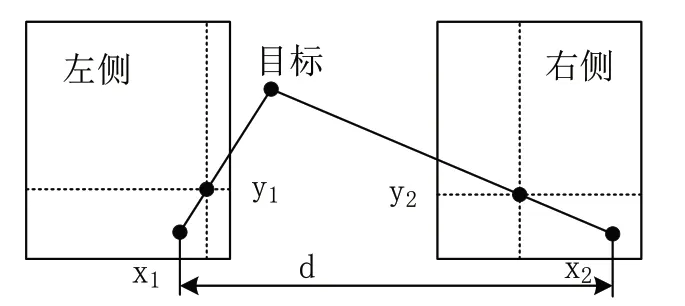
图1 相机平行位置假设
考虑环境温度、湿度以及压强等参数对相机内参数的影响,根据上述假设标定相机内参数[2]。将图像上的随机点p的像素记为p(x,y,1),要求该点与空间坐标P(x,y,z)对应,根据两个坐标对应的齐次坐标,得到关系式:
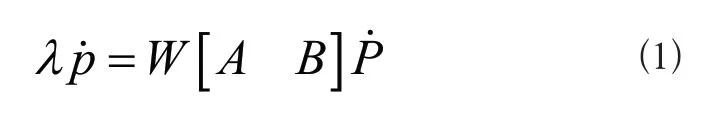
式中:λ表示尺度因子;p.、p.均表示齐次坐标;W、A、B表示相机的内参数和外参数矩阵。假设畸变系数为μ,保证μ1、μ2相互正交且形成的平面内不包含相机外参数B,根据上述假设条件,设置矩阵G=W[μ1μ2B]=[w1w2w3],则det(W)、det([μ1μ2B])以及det(G)的计算结果不为0,根据式(1)和上述矩阵G,可以推导出wTiCwi=uTijd,其中C表示转置矩阵。根据上述结果,得出基本约束方程为:
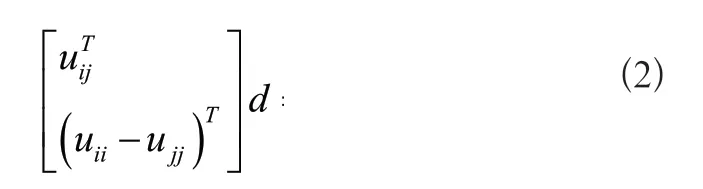
对目标物体拍摄n张图像,得到n个方程组,即Ud=0,导出d的值确定拍摄距离,实现对活动范围的标定。
1.2 检测视觉图像中的目标所在区域
在不断变化的视觉图像中,为了增强对目标的辨识,灰度化处理视觉图像,描述同一幅图中的局部色度和亮度,通过提取所有位置的色度和亮度分布特征,定位目标物体所在区域范围。对于目标物体来说,边缘图像的二值化处理效果,直接影响定位范围的准确性。根据现有图像处理方法可知,图像二值化处理的关键在于选择阈值。此次研究设定,若阈值使分割产生的误分割最少,那么该阈值为最优阈值。默认视觉图像中所有像素点的灰度值都服从正态分布,设置密度函数F1(x),利用该函数计算目标像素点灰度;设置密度函数F2(x),利用该函数计算背景点灰度。根据上述两个参数的均值η和方差σ、目标像素点占图像总像素点的比例R、背景点与图像总像素点的比例1-R,得到下列计算结果:
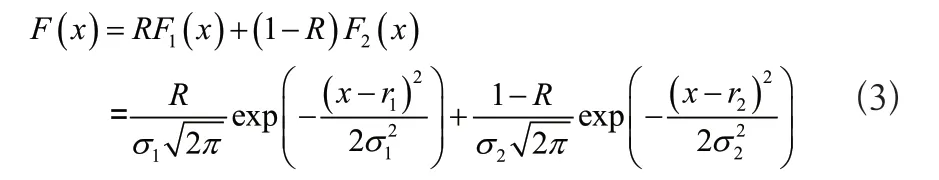
式中:r1、r2表示两幅图中的无意义像素点。假设阈值为K,该值的所在位置如图2所示。
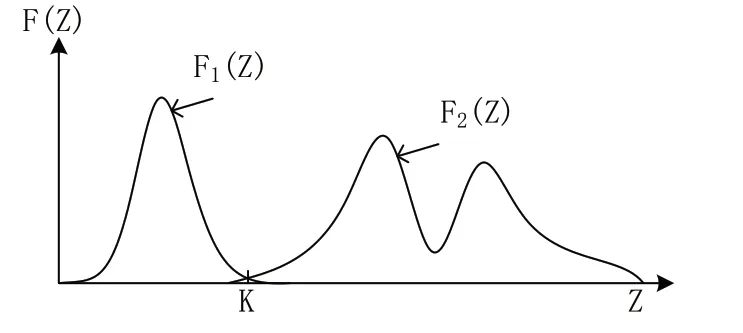
图2 目标像素、背景像素和阈值分布图
当灰度值小于K时和大于K时,像素为目标点或背景点[3]。假设目标点被误认为是背景点的概率为E1(K)、背景点被误认为是目标点的概率为E1(K),则通过下列计算公式,获得总误判概率:
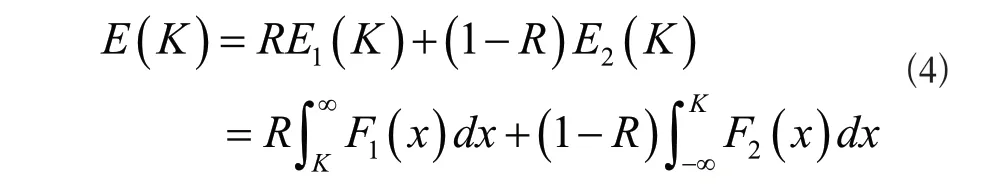
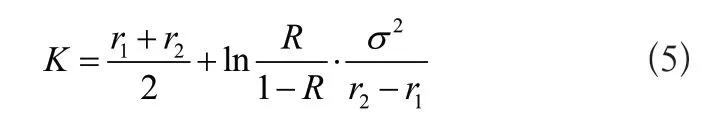
当目标点和背景点有相同分布时,阈值K最佳,可以实现对图像信息的分割,实现对视觉图像中目标所在区域的检测。
1.3 规划机器人运动轨迹
根据视觉图像目标物体所在方位检测结果,规划工业机器人的直线轨迹、圆弧轨迹。对直线运动轨迹方程插补处理,规划机器人的直线位置轨迹。假设视觉图像的目标物体检测范围内,轨迹的起点和终点位置坐标分别为qa和qb,则轨迹长度为L=|qb-qa|。假设起点和终点之间的中间点为qi,该点到起点qa的长度为L',则直线运动轨迹方程为:

对上述公式中的参数L'插值就能得到坐标qi。此次研究选择五次多项式插值法,在L'(0)=0和L'i(mi)=L两组条件下,得到五次多项式插值结果:
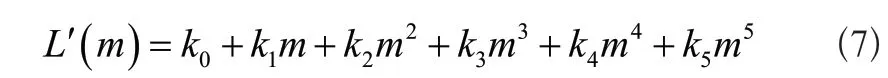
假设L'i(0)=0、L'i(mi)=0,根据两组条件和两组假设,通过式(7)得到k0、k1以及k2的值为0,其他参数的计算结果为:
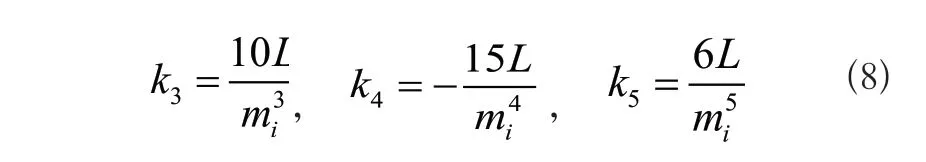
将上述6组结果代入到式(7)中,通过计算导出中间点qi的值,实现直线位置轨迹规划。但多自由度的工业机器人功能更加齐全,所以活动轨迹会更加多样灵活,因此针对圆弧位置规划运动轨迹。根据上述已知假设,设置圆弧起点、终点坐标以及中间点坐标,分别用qa=[xa,ya,za]Tqb=[xb,yb,zb]Tqi=[xi,yi,zi]T表示。设置中间点与起点之间的弧长为Li,建立圆弧运动轨迹方程,得到半径R要和圆弧圆心q0之间的几何关系,公式为:

式中:φ表示几何关系参数。根据上述计算导出3×3矩阵U和3×1矩阵V的关系为U[x0,y0,z0]T=V,以此导出圆弧圆心q0的坐标和半径R的值。将上述结果代入下列公式,得到以路径中间点为参数的圆弧运动轨迹方程:
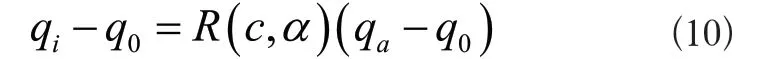
式中:c表示旋转轴;a表示圆心角[4]。综合直线位置和圆弧位置,实现对多自由度工业机器人不同活动轨迹的规划。
1.4 设计模糊PID控制器调节运动轨迹
多样化的机器人运动轨迹划分完毕后,需要依靠可靠的技术控制机器人按照规划的轨迹稳定运动。设计模糊PID控制器,如图3所示,通过该控制器稳定机器人的运行。

图3 模糊PID控制器结构图
模糊PID控制器共由三个主要模块组成,分别为模糊语言变量分类模块、语言变量隶属函数生成模块、模糊控制规则选取模块。设置控制器为二维模糊作为,设置二输入语言的位置误差和误差率分别为f和fc,三输出语言变量为tp、ti、td[5]。已知输入语言变量分为负大、负中、负小、零、小正、中正、大正共计7种类别,利用三角形隶属函数计算所有模糊子集,推到出位置误差和误差率的值,该值的取值范围在0~1之间。设置模糊PID控制器的运行规则:
当f较大时,认为机器人处于初始匀速运动阶段,为了提高机器人响应速度,调整tp和ti的值至最大,同时减小td的值,尽可能消除产生的误差;当f处于中等大小时,要同时控制机器人的位置误差和移动误差,所以将ti的值控制在最小,调节机器人的动作响应速度;当f较小时,为了加强机器人的运动稳定性,增加tp和ti的值消除稳态误差,但此时的微分作用会放大f,所以要求td的值尽可能最小。根据上述设计思路,通过下列公式调节控制器的运行:
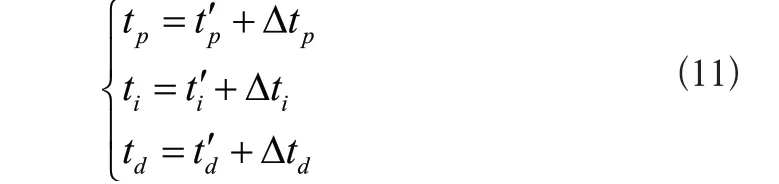
公式中:t'p、t'i、t'd为阶跃响应整定出来的PID参数;△tp、△ti以及△td为不同参数对应的活跃值。以规划的运动轨迹为前提,通过模糊PID控制器调节机器人运动轨迹,至此基于视觉图像的多自由度工业机器人轨迹控制方法完成设计。
2 应用与分析
2.1 搭建测试环境
测试环境由多自由度工业机器人、双目设备以及运动控制设备等主要硬件共同组成,其中多自由度工业机器人执行下达的工作指令、双目设备实现数据采集与特征提取功能、运动控制设备控制机器人执行各项指令。选择的机器人通过主动臂与从动臂的活动执行指令。双目视觉设备是此次研究轨迹控制方法中,全新的环节,通过RERVISION摄像头获取实时数据。该相机的镜头中心间距为65mm,利用HUB连接2路摄像头,保证2路摄像头同时工作,最终通过1根USB线传输给机器人。已知机器人软件部分由PLC和此次研究设计的模糊PID控制器共同组成,经由PC端控制机器人的正向和反向运动、路径规划等。该机器人的软件主要执行三项功能:
1)将机器人动作级指令上传到控制指令区,观察机器人运动情况,该过程中的代码通过双目设备自动获取并生成。
2)在机器人的控制区建立通信连接,管控机器人的启动、运动、线路调整、停止等操作,为了将实验误差控制在最小范围内,所有控制只在PC端的软件界面中完成,不再设置其他人机交互设备。
3)设定机器人的运动范围,按照上、下、左、右、前、后共6个方向设置点,同时要求双目设备支持同步功能,也就是要求双目设备能直接向机器人反馈实时环境数据以及自身运动数据。
根据上述内容准备测试工具,检查图4所示的设备和工具是否可以使用,测试此次研究的机器人轨迹控制方法的应用效果。

图4 测试工具
将不同颜色的白板笔安装到机器人机械臂末端,通过控制机器人运动姿态,让机器人在白纸板上画出完整的蝴蝶轮廓,分析本文研究方法是否更加稳定。
2.2 轨迹控制效果
将基于NURBS算法的控制方法作为对照A组,将基于布谷鸟算法的控制方法作为对照B组,将本文的轨迹控制方法作为实验组,要求三组方法在白纸板的左上、右上、左下、右下分别绘制4个完整的蝴蝶轮廓,结果如图5所示。
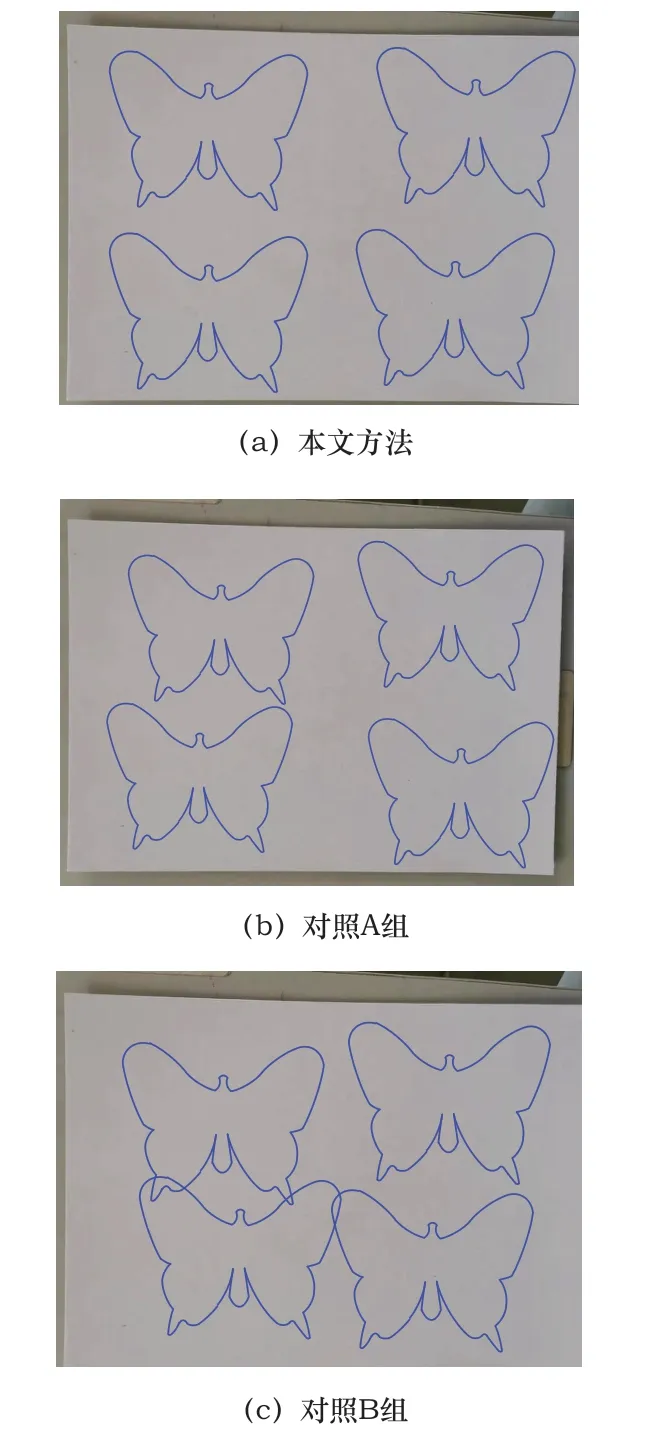
图5 轨迹控制效果
根据上图显示的蝴蝶形状可知,本文方法和对照A组方法获得了预期的结果,但对照B组的白纸板上有3组蝴蝶形状的边缘轮廓重叠,说明对照B组方法的控制效果最差。将机器人机械臂末端的蓝色白板笔换成红色,按照白纸板上现有的蝴蝶形状,再次绘画蝴蝶轮廓,要求红色轮廓与蓝色轮廓重合,得到的结果如图6所示。
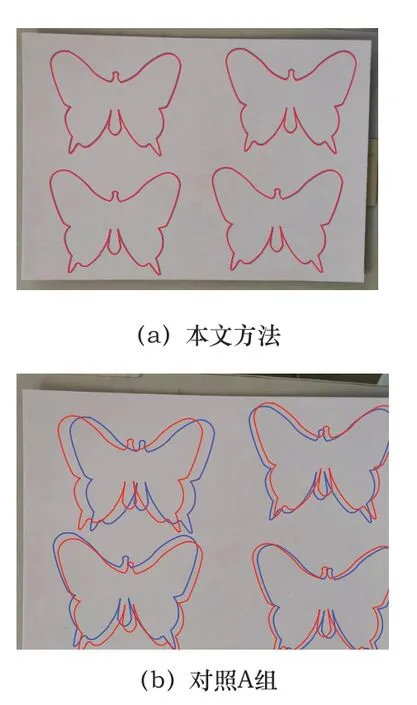
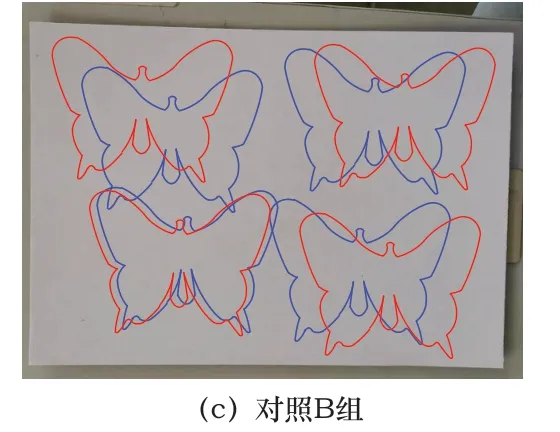
图6 覆盖轨迹控制效果
根据上图显示的测试结果可知,要求覆盖原有蝴蝶形状时,只有本文方法得到了理想覆盖效果,对照A组和对照B组的覆盖效果较差,尤其对照B组的蝴蝶轮廓,与已有的轮廓之间存在的差异最大。根据上述实验测试结果,认为本文方法的控制效果最佳。
2.3 控制误差对比实验
根据上述测试结果,比较轨迹控制误差,验证不同方法应用下,多自由度机器人运动姿态的稳定性。已知机器人的功率为260W,关节电机减速比为85∶1,关节转角范围在±105°范围内,最大转速为1.0转/秒。实验设置测试时间为1000ms,通过不同控制方法实现对18Hz正弦信号的控制,得到前700ms的轨迹控制误差,结果如图7所示。

图7 轨迹控制误差
根据上图曲线可知,三组方法均存在控制误差,其中实验组的控制误差范围在±0.5cm之间;对照A组的控制误差在±1.5cm之间;对照B组的控制误差在±4.5cm之间。已知数据的正、负代表误差方向,不影响数据计算。导出1000ms测试时间内完整的测试误差数据,结果如表1所示。
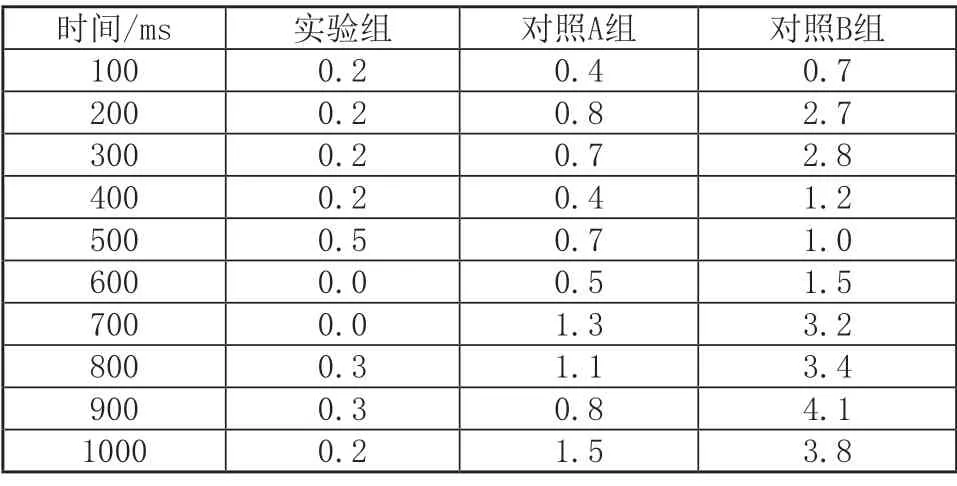
表1 轨迹控制误差(cm)
计算三组方法对轨迹控制产生的平均误差,分别为0.21cm、0.82cm以及2.44cm。综合上述测试结果可知,本文方法的轨迹误差控制效果更好,说明通过视觉图像能够获得更加精准的控制范围,增强了模糊PID控制对机器人稳定性的控制。
3 结语
此次研究以视觉图像为新的研究重点,通过视觉图像帮助模糊PID控制器加强轨迹控制效果,增强了机器人工作的稳定性。此次研究是针对多自由度工业机器人设计的,对于利用该方法控制其他自由度工业机器人的轨迹效果,还有待验证,因此在使用该方法之前需要明确使用对象,防止出现误差较大的情况。
