基于Plackett-Burman试验设计与响应面法优化玉米秸秆离散元模型

朱惠斌 钱 诚 白丽珍* 李 慧 牟丹磊 李骏杰

(1.昆明理工大学 农业与食品学院，昆明 650500； 2.山东省农业机械科学研究院，济南 250010)

我国的玉米种植长期采用传统耕作模式，存在土壤有机碳含量降低、耕层厚度减小、土壤潜在生产力降低等问题[1-3]。保护性耕作具有改善土壤理化性质、增强土壤蓄水保墒能力和提高土壤微生物群落数量等显著效益[4-6]。免耕播种机是在玉米种植区进行保护性耕作的重要农机具。防堵装置是免耕播种机的核心部件，其主要作用是切断或拨离秸秆从而保证免耕播种施肥作业的顺利进行。为提高免耕播种机防堵装置的作业性能，应对其进行数值模拟，从而对防堵装置的结构进行优化改进。防堵装置数值模拟的关键点是建立可破碎的玉米秸秆模型，从而对切割或拨离秸秆的过程进行数值模拟。

目前，机械部件的数值模拟方法主要为有限元法[7-8]和离散元法[9-10]，尤其在农业机械设计与理论分析方面，如对冰草种子[11]和花生[12]进行建模，对深松铲[13]、开沟器[14]、旋耕刀[15]和排种器[16]等进行优化改进。离散元法可用于模拟免耕播种机防堵装置的作业过程，为防堵装置优化提供理论依据，如已有研究建立玉米秸秆层离散元模型[17]和小麦秸秆离散元模型[18-19]对防堵装置进行数值模拟。但上述基于Hertz-Mindlin (no slip)模型建立的秸秆离散元模型存在局限性，这些秸秆模型不会因外力而发生断裂或破坏，无法对防堵装置切割秸秆的过程进行数值模拟。为对防堵装置切割或拨离秸秆过程进行数值模拟，以Hertz-Mindlin with bonding模型为接触模型建立可破碎的玉米秸秆离散元模型。

采用离散元法对免耕播种机防堵装置进行数值模拟时，需对秸秆离散元模型进行参数标定从而减小数值模拟的误差。已有研究主要采用堆积角试验对各类离散元模型进行标定，如苜蓿秸秆[20]、油菜茎秆[21]、水稻种子[22]、胡麻籽粒[23]和三七种子[24]。堆积角试验标定法不能准确反映出离散元模型的力学特性，因此采用单轴压缩试验法对玉米秸秆离散元模型进行标定，以减小免耕播种机防堵装置数值模拟的误差。

本研究拟对玉米秸秆进行物理单轴压缩试验，基于Hertz-Mindlin with bonding接触模型建立玉米秸秆离散元模型；以物理试验与仿真试验的临界载荷相对误差为试验指标，采用单因素试验法、Plackett-Burman试验设计和Box-Behnken响应面法确定离散元模型的最优仿真参数组合；以期为免耕播种机防堵装置的数值模拟提供仿真参数依据。

1 材料与方法

1.1 玉米秸秆物理单轴压缩试验

试验材料选用昆明理工大学保护性耕作试验田种植的“红单6号”玉米，在玉米收获2周之后采集秸秆。选取粗壮笔直的节间玉米秸秆为试样，标距为60 mm，直径为25.67 mm，含水率约为53.6%。试验设备为CSS-44100万能材料试验机，最大载荷100 kN。以10 mm/min加载速度和10 kN加载力进行单轴压缩试验，试验重复9次。根据试验结果，玉米秸秆单轴压缩试验的临界载荷为935.4 N。

1.2 玉米秸秆仿真单轴压缩模型

1.2.1The Hertz-Mindlin with bonding接触模型

The Hertz-Mindlin with bonding接触模型是基于Potyondya提出的颗粒粘结模型(Bonded particle model，BPM)，主要用于物料破碎、磨损的模拟(图1)[25]。该接触模型采用有限尺寸的粘结键将颗粒粘结，粘结键可以抵抗切向和法向位移，直至达到最大法向和切向剪应力使粘结键断裂。此后，粒子以硬球的形式相互作用。在粘结键产生前，通过Hertz-Mindlin接触模型计算颗粒间的相互作用。

在某一时刻粘结键产生后，将粘结力和力矩设置为零，求出在每个时间步所受粘结力和力矩的叠加增量。表达式如下：

Fn=-vnSnAδt

(1)

Ft=-vtStAδt

(2)

Mn=-ωnStJδt

(3)

(4)

式中：Fn为法向粘结力，N；Ft为切向粘结力，N；δt为时间步长，s；Mn为法向力矩，N·m；Mt为切向力矩，N·m；Sn为法向刚度，N/m3；St为切向刚度，N/m3；vn为法向速度，m/s；vt为切向速度，m/s；ωn为法向角速度，rad/s；ωt为切向角速度，rad/s；A为

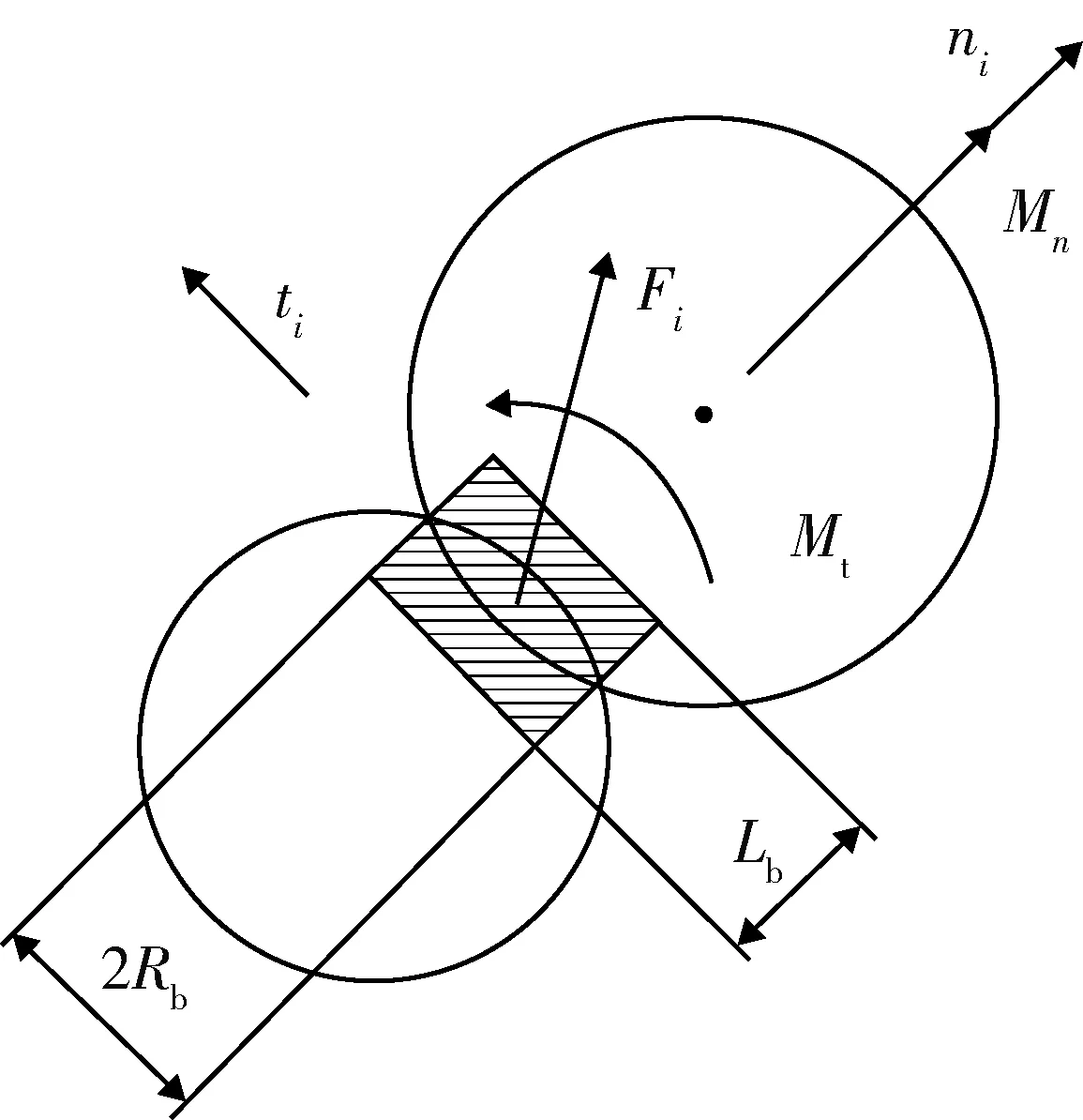
ti表示切线方向；ni表示法线方向。 Mt，切向力矩；Mn，法向力矩；Fi，粘结力；Rb，粘结键半径；Lb，粘结键长度。 ti, tangent direction; ni, normal direction. Mt, tangential moment; Mn, normal moment; Fi, bonding force; Rb, radius of bond; Lb, length of bond.图1 The Hertz-Mindlin with bonding接触模型Fig.1 The Hertz-Mindlin with bonding contact model

当模型中粘结键的法向应力σmax和切向应力τmax到达临界值时，粘结键产生破坏，表达式如下：

(5)

(6)

1.2.2玉米秸秆离散元模型

玉米秸秆可分为内瓤和外表皮，属于各向异性材料。本研究的玉米秸秆离散元模型主要用于免耕播种机防堵装置的数值模拟，只需保证玉米秸秆离散元模型能体现秸秆的力学特性。在实际建模时，对玉米秸秆进行简化，将秸秆等效为各向同性材料。基于离散元法建立玉米秸秆离散元模型，以颗粒之间产生粘结键来体现玉米秸秆的力学性能。采用颗粒快速填充法建立玉米秸秆离散元模型，建模流程见图2。

基于Gambit软件对玉米秸秆进行几何建模，设置其半径为13 mm，高为60 mm。对几何模型进行网格划分，设置spacing为3、网格类型为四面体网格，完成网格划分。将已划分网格的几何建模导入刀Fluent软件中，以用户自定义函数下Compiled UDFs命令导入编写好的C文件，对C文件进行编译，得到包含颗粒坐标的文件。C文件可根据用户定义的最大填充系数和基础半径，求出几何体所有网格的中心坐标，最后生成有关颗粒坐标、速度和粒径倍数等信息的文档。设置最大填充系数为0.61，基础半径为1 mm。

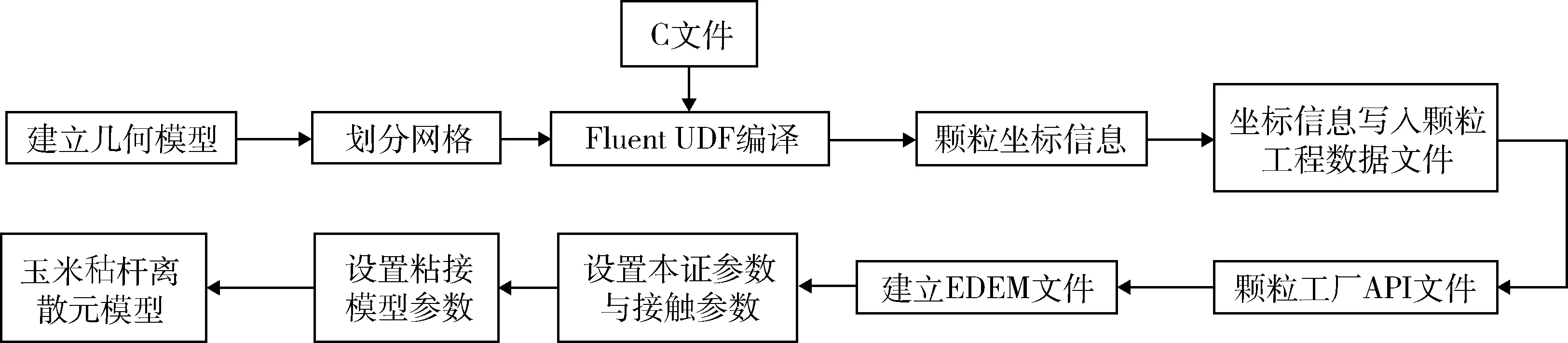
图2 离散元模型建立流程Fig.2 Process of building discrete element model

建立EDEM文件，对颗粒与几何模型的本征参数和接触参数进行设置，如表1所示[26]。设置颗粒的半径为1 mm，接触半径根据试验方案进行设置。把颗粒坐标数据复制到颗粒工厂数据文件“Block_Factory_Data.txt”中，将颗粒工厂API文件“myFactory.dll”导入EDEM。设置颗粒之间的接触模型为“The Hertz-Mindlin with bonding”，相关参数根据试验方案进行设置。将划分好网格的玉米秸秆模型导入，设置时间步长为Rayleigh的时间步长2%，完成玉米秸秆离散元模型的建立(图3)。

基于后处理功能将粘结完成的秸秆离散元模型输出为“.edm”文件，将压板与支撑底座的几何模型导入输出文件，为压板添加Force Controller，设置压缩力为10 kN，速度为10 mm/min，玉米秸秆仿真单轴压缩试验模型见图4。

表1 颗粒与几何模型的仿真参数Table 1 Simulation parameters of particle and geometric model

图3 玉米秸秆离散元模型Fig.3 Discrete element model of corn stalk

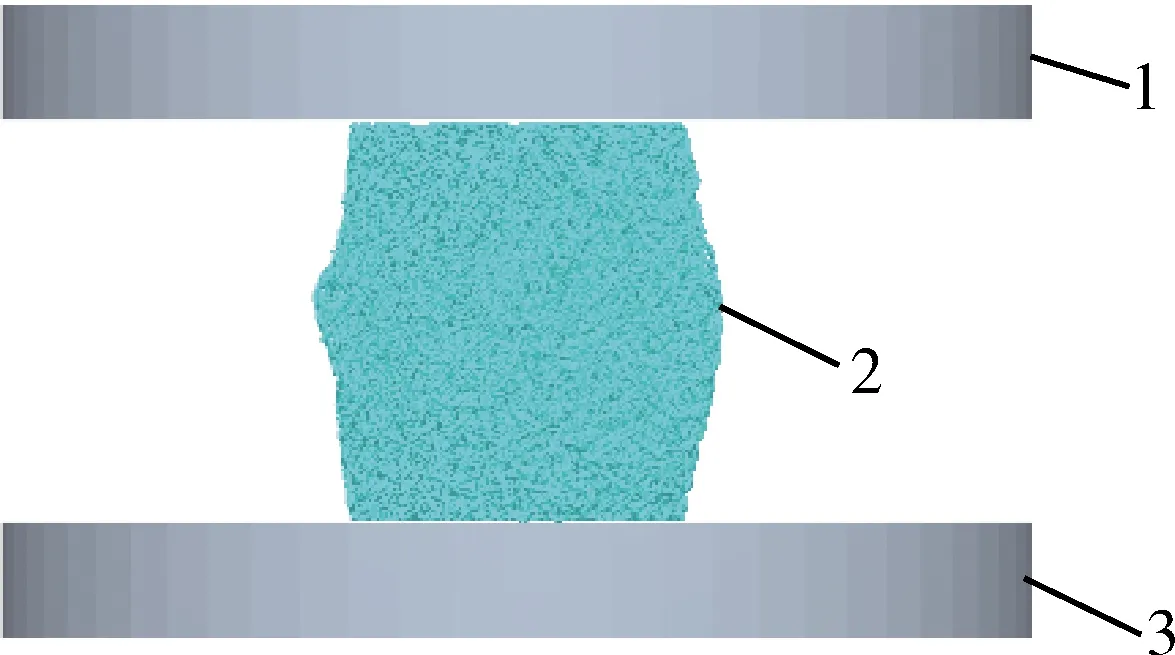
1.压板；2.玉米秸秆；3.支撑底座 1.Compression; 2.Corn stalk; 3.Support base图4 仿真压缩试验模型Fig.4 Model of simulated compression test

1.3 试验因素与试验指标

选取接触半径和Hertz-Mindlin with bonding接触模型的相关参数为试验因素，根据前期试验结果，选取因素的试验水平见表2。在仿真单轴压缩试验完成之后，导出压板在每个时间步所受到力的数据文件，根据牛顿第三定律，该力等效为玉米秸秆在压缩过程中所受到的力，以其峰值为玉米秸秆所受到的临界载荷。试验以仿真试验与物理试验中玉米秸秆所受到的临界载荷的相对误差为试验指标，根据式(7)进行计算：

(7)

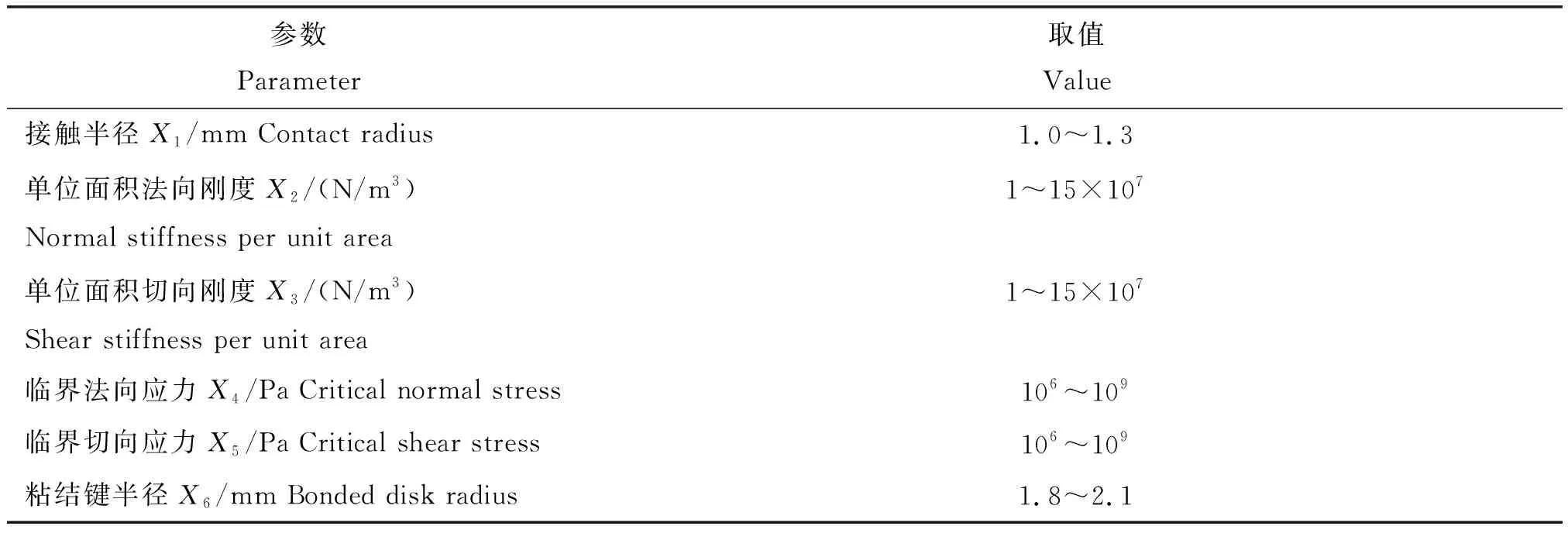
表2 Hertz-Mindlin with bonding接触模型参数Table 2 Parameters contact model of Hertz-Mindlin with bonding

式中：ER为物理试验与仿真试验的相对误差，%；Fsmax为在仿真单轴压缩试验中玉米秸秆所受到的临界载荷，N；Fpmax为在物理单轴压缩试验中玉米秸秆所受到的临界载荷，N。

1.4 试验设计

1.4.1单因素试验设计

以仿真试验与物理试验中玉米秸秆所受到的临界载荷的相对误差为试验指标，对6个试验因素进行单因素试验，分析各个因素对相对误差的变化规律。单因素试验采用的固定参数分别为：接触半径1.2 mm、单位面积法向刚度1×108N/m3、单位面积切向刚度1×108N/m3、临界法向应力1×108Pa、临界切向应力1×108Pa和粘结半径2 mm。

1.4.2Plackett-Burman试验设计

Plackett-Burman试验设计法在可在试验因素较多的条件下，选取试验因素的两个高低水平进行试验设计来筛选出对试验结果有显著影响的因素。在单因素试验的基础上，对接触半径、单位面积法向刚度、单位面积切向刚度、临界法向应力、临界切向应力和粘结半径共6个试验因素进行筛选，得到对相对误差影响显著的因素，设计了试验次数N=12的Plackett-Burman试验。

1.4.3最陡爬坡试验

根据Plackett-Burman试验结果，对具有显著性的因素(接触半径、单位面积法向刚度和单位面积切向刚度)进行最陡爬坡试验，使试验因素水平快速逼近最优范围，以进行Box-Behnken响应面法试验。

1.4.4Box-Behnken响应面法试验设计

根据最陡爬坡试验试验的结果，以接触半径、单位面积法向刚度和单位面积切向刚度为自变量，相对误差为响应值，进行Box-Behnken响应面试验。设计3因素3水平共17次的响应面试验，探究变量对响应值的影响，因素试验因素和水平见表3。

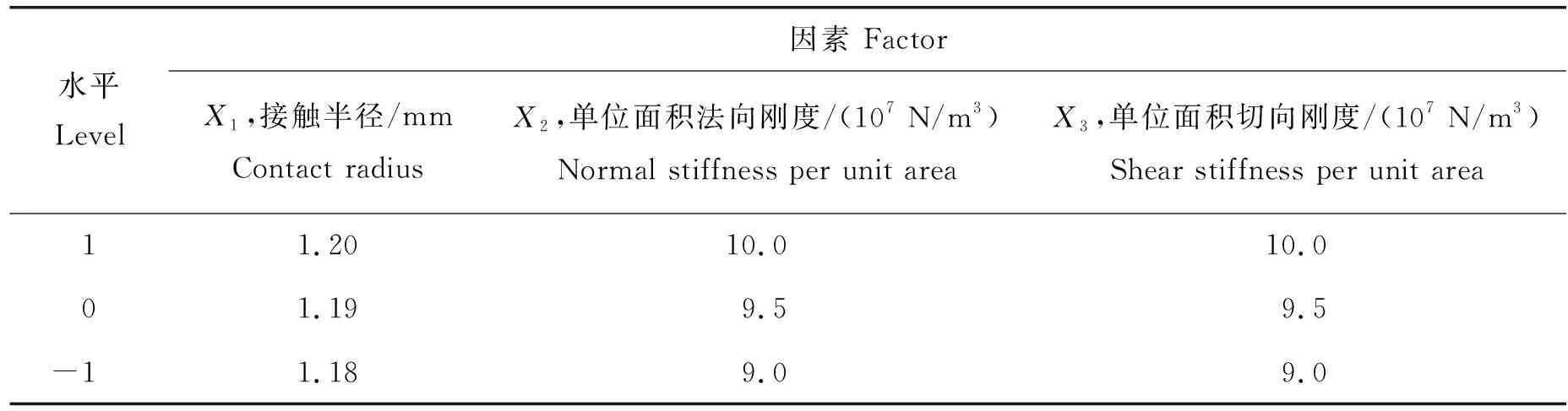
表3 Box-Behnken试验因素与水平Table 3 Experimental factors and levels of Box-Behnken

2 结果与分析

2.1 单因素试验

1)随着接触半径增大，相对误差先减小然后增大，这是由于接触半径增大使粘结键的数量增加，导致临界载荷增大(图5(a))。接触半径为1.2 mm时，相对误差最小。

2)随着单位面积法向刚度增加，相对误差先减小然后增大(图5(b))。这是由于单位面积法向刚度增大使颗粒之间粘结力增加，导致临界载荷增大。单位面积法向刚度为1×108N/m3时，相对误差最小。

3)随着单位面积切向刚度增加，相对误差先减小然后增大(图5(c))。这是因为单位面积切向刚度增大使颗粒之间粘结力增加，从而提高玉米秸秆离散元模型抵抗变形和破坏的能力，最终导致临界载荷增大。单位面积切向刚度为1×108N/m3时，相对误差最小。

4)随着临界法向应力增加，相对误差的变化不大(图5(d))。临界法向应力为1×108Pa时，相对误差最小。

5)随着临界切向应力增加，相对误差先减小后增大，但变化幅度不大(图5(e))。临界切向应力为1×108Pa时，相对误差最小。

6)随着粘结键半径增加，相对误差先减小后增大(图5(f))。这是因为粘结键半径增大使颗粒粘结力增大，导致临界载荷变大。粘结键半径为2 mm 时，相对误差最小。

X1，X2，…，X6的含义见表2，下表、图同。 The meanings of X1， X2， …， X6 are shown in Table 2, and the following Tables and Figures are the same.图5 各因素对物理试验与仿真试验相对误差的影响Fig.5 Effect of factors on relative error of physical test and simulation test

2.2 Plackett-Burman试验

Plackett-Burman试验结果见表4，对试验结果进行方差分析，结果见表5。可知：决定系数R2为0.97，说明模型适用于97.44%的试验数据；X1和X3

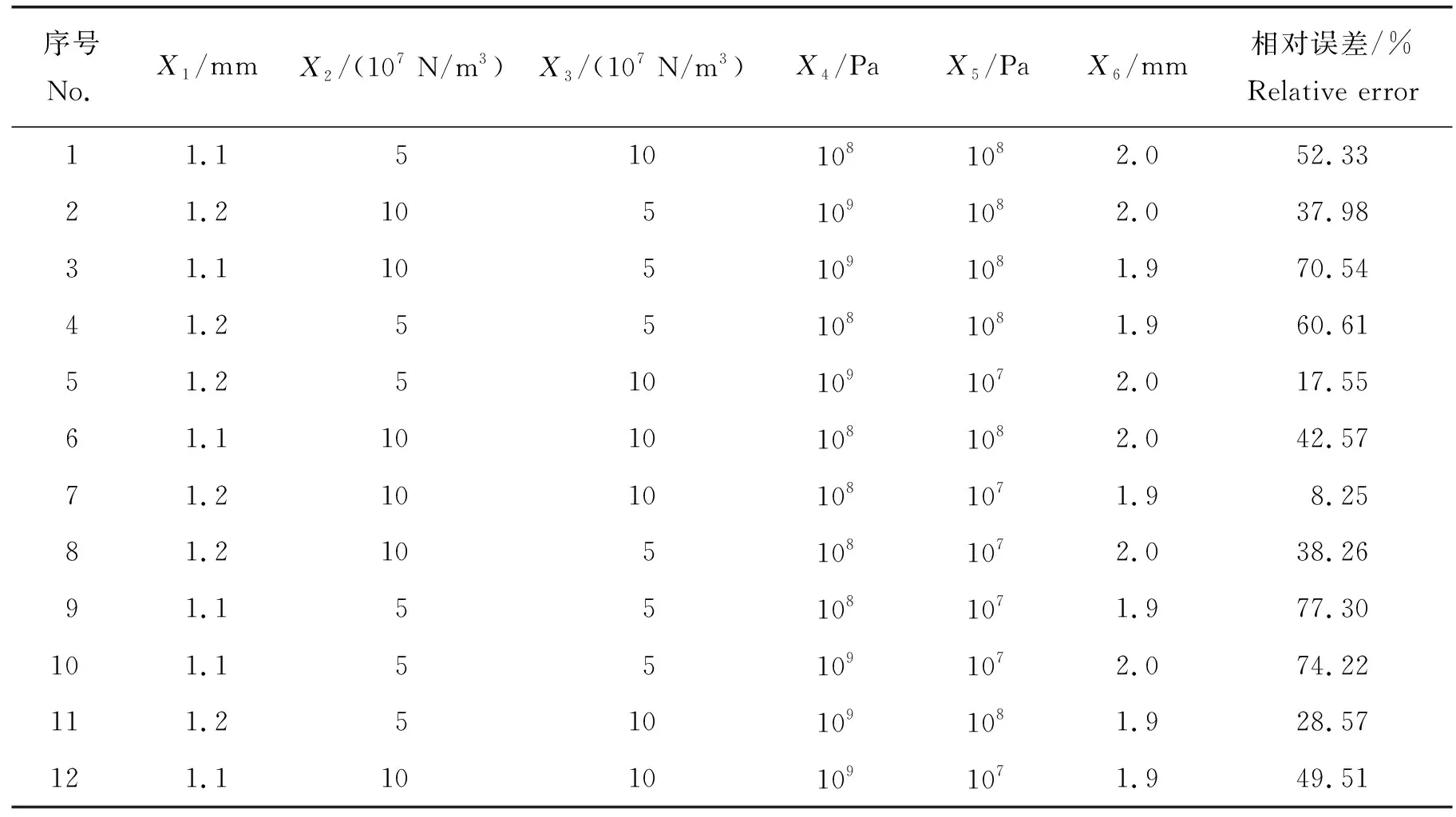
表4 Plackett-Burman试验结果Table 4 Test result of Plackett-Burman

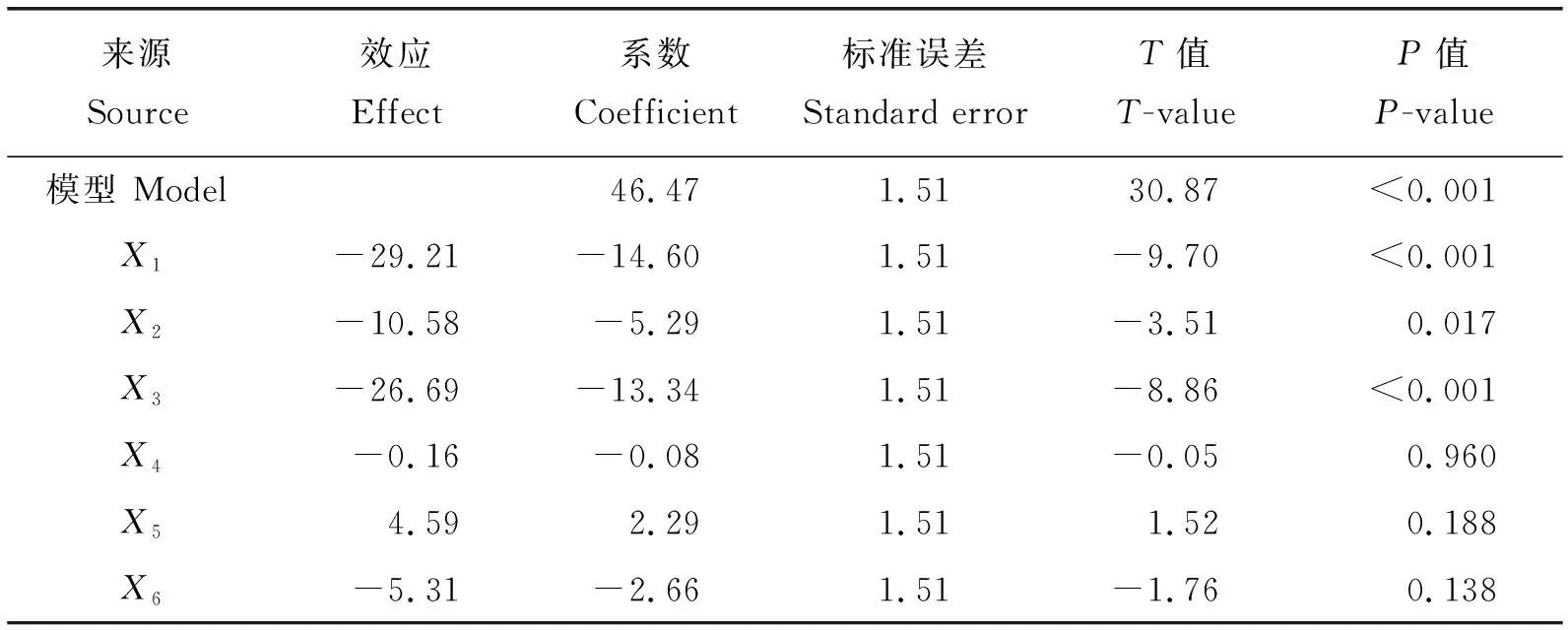
表5 Plackett-Burman试验方差分析Table 5 ANOVA for the Plackett-Burman design

的P<0.01，表明接触半径和单位面积切向刚度对相对误差的影响极显著；X2的P<0.05，即单位面积法向刚度对相对误差的影响显著；X4、X5和X6的P>0.05，说明粘临界法向应力、临界切向应力和粘结键半径对相对误差的影响不显著。因此，选取因素X1、X2和X3进行最陡爬坡试验和中心组合响应面试验。在进行最陡爬坡试验和中心组合响应面试验时，根据单因素试验结果取不显著因素的水平为：临界切向应力1×108Pa、临界切向应力1×108Pa和粘结键半径2 mm。

2.3 最陡爬坡试验

最陡爬坡试验的结果见表6，可知：试验5与试验6的临界载荷分别为775.73和986.85 N。玉米秸秆物理单轴压缩试验的临界载荷为935.4 N，在试验5与试验6的结果区间之内，而且试验5与试验6的相对误差较小，因此选取试验5和试验6的因素水平分别为Box-Behnken试验低水平和高水平。

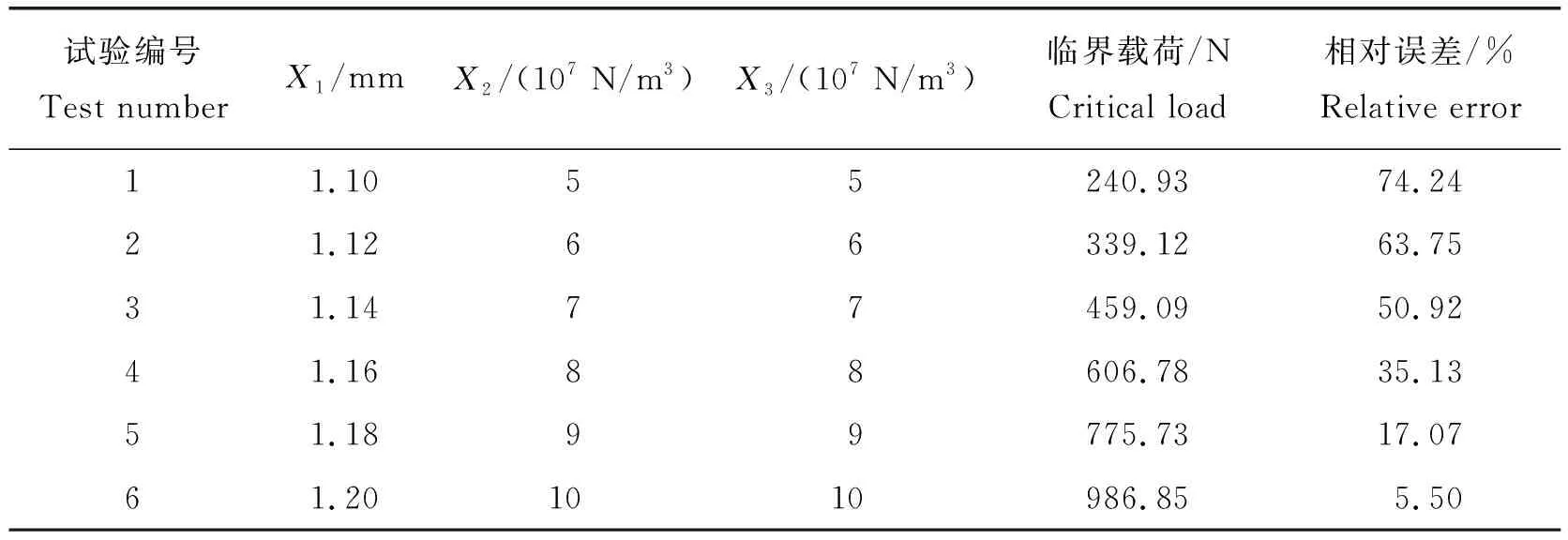
表6 最陡爬坡试验结果Table 6 The path of steepest ascent design and results

2.4 Box-Behnken试验

为得到离散元模型参数的最优组合，进行Box-Behnken试验，结果见表7。对试验结果进行回归拟合后，得到以相对误差为响应值，X1(接触半径)、X2(单位面积法向刚度)和X3(单位面积切向刚度)为变量的回归方程：

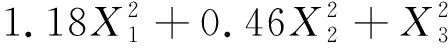
(8)

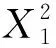
根据回归方程得到各因素交互作用对物理试验与仿真试验相对误差影响的响应面图(图6)。

表7 Box-Behnken试验结果Table 7 Experimental results of Box-Behnken

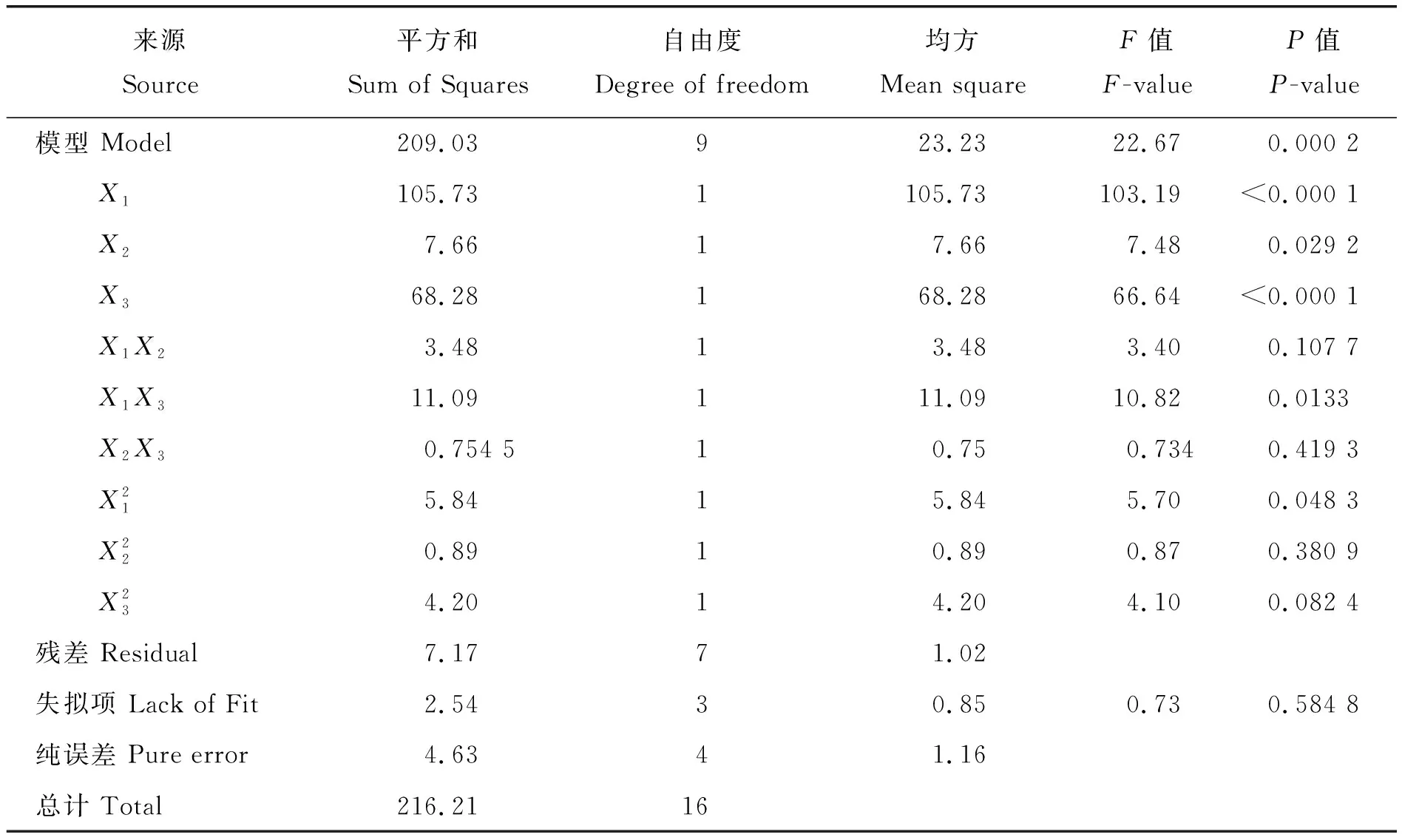
表8 Box-Behnken回归模型的方差分析Table 8 ANOVA for Box-Behnken quadratic model

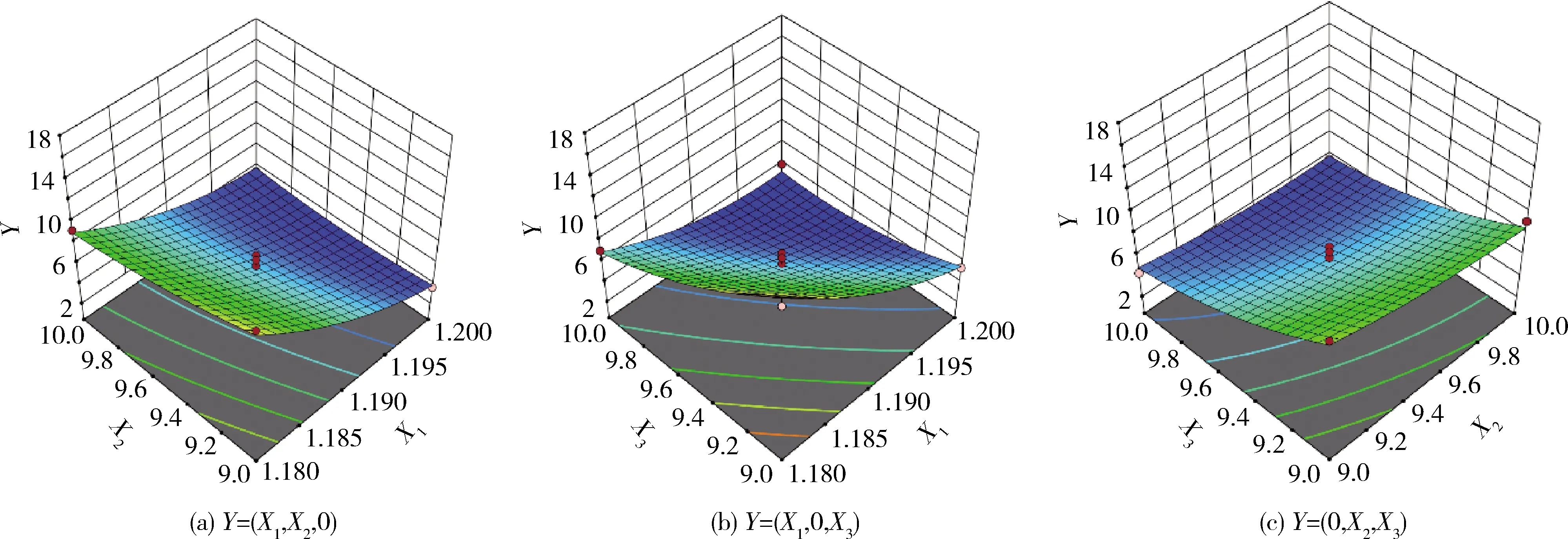
Y为玉米秸秆临界载荷试验值与仿真值之间的相对误差。 Y was relative error between the critical load test value and simulation value of corn stalk.图6 交互作用对物理试验与仿真试验相对误差的影响Fig.6 Effect of interaction factors on relative error of physical test and simulation test

当单位面积法向刚度为定值时，相对误差随着接触半径的增大，呈减小趋势，变化幅度明显，接触半径对相对误差的影响高于单位面积法向刚度的影响(图6(a))。

接触半径与单位面积切向刚度的交互作用对相对误差的影响明显(图6(b))。当接触半径为定值时，随着单位面积切向刚度的增大，相对误差呈先减小后增大的趋势；当单位面积切向刚度的增大为定值时，随着接触半径的增大，相对误差呈减小趋势，且变化幅度明显。

由图6(c)可知，当接触半径为固定水平值时，单位面积法向刚度与单位面积切向刚度的交互作用对相对误差的影响不显著。当单位面积法向刚度为定值时，相对误差随着单位面积切向刚度的增大，呈减小趋势，单位面积切向刚度对相对误差的影响高于单位面积法向刚度的影响。

2.5 最优参数与模型验证

为了使仿真单轴压缩试验中玉米秸秆所受到的临界载荷接近物理试验的935.4 N，采用Design-Expert软件对回归模型进行优化分析，得到最优仿真参数为：接触半径1.2 mm、单位面积法向刚度9.361×107N/m3和单位面积切向刚度9.845×107N/m3，预测理论相对误差为2.94%。根据最优仿真参数进行验证试验，玉米秸秆离散元模型在验证试验中临界载荷为950.2 N，与物理试验的相对误差为1.58%，试验结果与预测值基本一致，进一步证明了模型的准确性与可靠性。

3 结 论

本研究基于Plackett-Burman试验设计和Box-Behnken响应面法，以单轴压缩试验法对玉米秸秆离散元模型进行标定，探究了玉米秸秆离散元模型的最优参数组合，主要结论如下：

1)进行物理试验测定得到玉米秸秆单轴压缩试验的临界载荷为935.4 N。开展Plackett-Burman试验，筛选出对临界载荷试验值与仿真值之间的相对误差有显著影响的因素为：接触半径、单位面积法向刚度和单位面积切向刚度。

2)进行最陡爬坡试验缩小显著性因素的水平范围，再进行Box-Behnken响应曲面试验，对试验结果进行方差分析，得到二次多项式回归方程。方差分析表明，回归方程极显著，且拟合度高。对回归方程进行优化求解，得到最优参数为：接触半径1.2 mm、单位面积法向刚度9.361×107N/m3和单位面积切向刚度9.845×107N/m3。进行验证试验，验证试验的临界载荷为950.2 N，与物理试验935.4 N的相对误差为1.58%，验证了玉米秸秆离散元模型的仿真参数的可靠性。