一种基于改进时间卷积网络的生猪价格预测方法

王泽鹏 陈晓燕* 庞 涛 余 富 胡肖楠 汪 震

(1.四川农业大学 信息工程学院，四川 雅安 625014； 2.农业信息工程四川省高校重点实验室，四川 雅安 625014； 3.四川农业大学 机电学院，四川 雅安 625014)

生猪是我国农产品市场中最基本、最重要的组成部分，生猪价格是农产品市场的核心要素[1]。受较多因素影响，生猪价格存在一定的波动和异常。生猪价格的不确定性增加了参与猪肉供应链的利益相关者所面临的风险，该风险可能损害生猪行业从业者的利益，这不仅不利于生猪产业的健康发展，也不利于国家经济的健康发展。鉴于生猪价格也是市场物价的重要组成部分，科学的预测方法可以帮助政府，生猪养殖厂等群体及时做出正确的决策，为广大人民群众的利益提供有利保障。

目前，生猪价格预测方法主要从传统农产品价格预测方法中迁移而来。已有研究对农产品价格预测提出了许多简化的计算模型以及相应的分析方法：1)最简单的多元线性回归模型[2]；2)ARIMA时间序列分析模型[3]；3)灰色双指数平滑法模型[4]；4)传统的机器学习模型[5-9],其中，传统的机器学习模型是应用最多和预测效果较好的方法。因为影响猪肉价格的因素较多，所以猪肉价格数据通常是非平稳的、非线性的，以上的研究方法存在预测精度不够高、容易陷入局部极小值等问题。神经网络具有强大的非线性计算能力，能够以任意精度近似任意连续的非线性函数，可以应用于具有输入和输出之间一定关系的任何价格预测，它可以很好地捕捉复杂的非线性模式。近年来，神经网络、深度学习等方法也逐渐地应用到农产品价格预测研究中，如对中国大豆价格[10]、鱼价[11]、多种农产品价格[12]等预测，也应用到了生猪价格[13-14]预测研究中，但预测精度有待提高。

时间卷积网络(TCN)[15]是深度学习领域中一种可以用来解决时间序列预测的算法，不仅具有高度的非线性逼近能力和很强的自学习能力，而且在处理大批量数据时，预测效果更优。Pelletier等[16]将时间卷积网络应用于卫星图像分类，Kim等[17]使用深度时间卷积网络预测生物遗传变异的突变效应。本研究拟采用改进网络结构的时间卷积网络模型，以西南地区某省的生猪价格数据为样本，进行生猪价格预测研究，以期为政府和企业提供科学的决策依据。

1 材料与方法

1.1 样本

试验数据来源于西南地区某省2011—2020年每周生猪价格，试验中按照时间顺序将每5周时间段中的前4周猪价作为单个样本的特征，第5周猪价作为对应的标签，设生猪价格周数据为xi,(i=0,1,…,n)，则单个样本的特征和对应的标签映射如下：

feature=xi,xi+1,xi+2,xi+3→label=xi+4(i=0,1,…,n-4)

(1)

式中：feature为单个样本的特征；label为对应的标签；→代表一一映射关系。总计产生476个样本数据，随机打乱后按照8∶2划分原则划分出385个样本数据作为训练集，91个样本数据作为测试集。

1.2 数据预处理

为将不同量级的数据统一转化为同一个量级，以保证数据之间的可比性，对数据进行了Z-Score标准化处理。公式如下：

(2)

式中：x为样本观测值；μ为总体平均值；σ为总体标准差；Z为样本标准化后的值。

1.3 建模方法

本研究所有试验均在训练集上采用5折交叉验证法划分为子训练集和子验证集，进行模型超参数选择，选取最佳超参数后，重新训练整个训练集得到最佳模型，然后在测试集上测试模型效果。其中机器学习方法在交叉验证的基础上对训练集进行网格搜索选取最佳超参数，神经网络方法在交叉验证的基础上对训练集进行调参、改进网络结构选取最佳超参数。训练集训练时5折交叉验证见图1。

1.3.1机器学习方法

1)随机森林回归(RFR)。随机森林属于Bagging类算法，而Bagging 又属于集成学习一种方法。集成学习的大致思路是训练多个弱模型打包起来组成一个强模型，强模型的性能要比单个弱模型好很多。在训练阶段，随机森林使用bootstrap采样从输入训练数据集中采集多个不同的子训练数据集来依次训练多个不同决策树；在预测阶段，随机森林将内部多个决策树的预测结果取平均得到最终的结果。

2)极限梯度提升(XGBoost)。极限梯度回升是基于决策树的集成机器学习算法，它以梯度提升(Gradient boost)为框架，由梯度提升决策树(GBDT)发展而来，同样是利用加法模型与前向分步算法实现学习的优化过程，但与梯度提升决策树

图1 训练集训练时5折交叉验证示意图Fig.1 Five-fold cross-validation diagram in the training set

是有区别的，主要是在目标函数、优化方法、缺失值处理、防止过拟合4个方面对梯度提升决策树进行了改进。

3)轻型梯度提升机(LightGBM)。轻型梯度提升机和极限梯度提升一样是对梯度提升决策树(GBDT)的高效实现，原理上它和GBDT及XGBoost类似，都采用损失函数的负梯度作为当前决策树的残差近似值，去拟合新的决策树。它的设计思路主要是减小数据对内存的使用，保证单个机器在不牺牲速度的情况下，尽可能地用上更多的数据；减小通信的代价，提升多机并行时的效率，实现在计算上的线性加速。

本研究随机森林回归试验、极限梯度提升试验、轻型梯度提升机试验网格搜索超参数变量见表1。

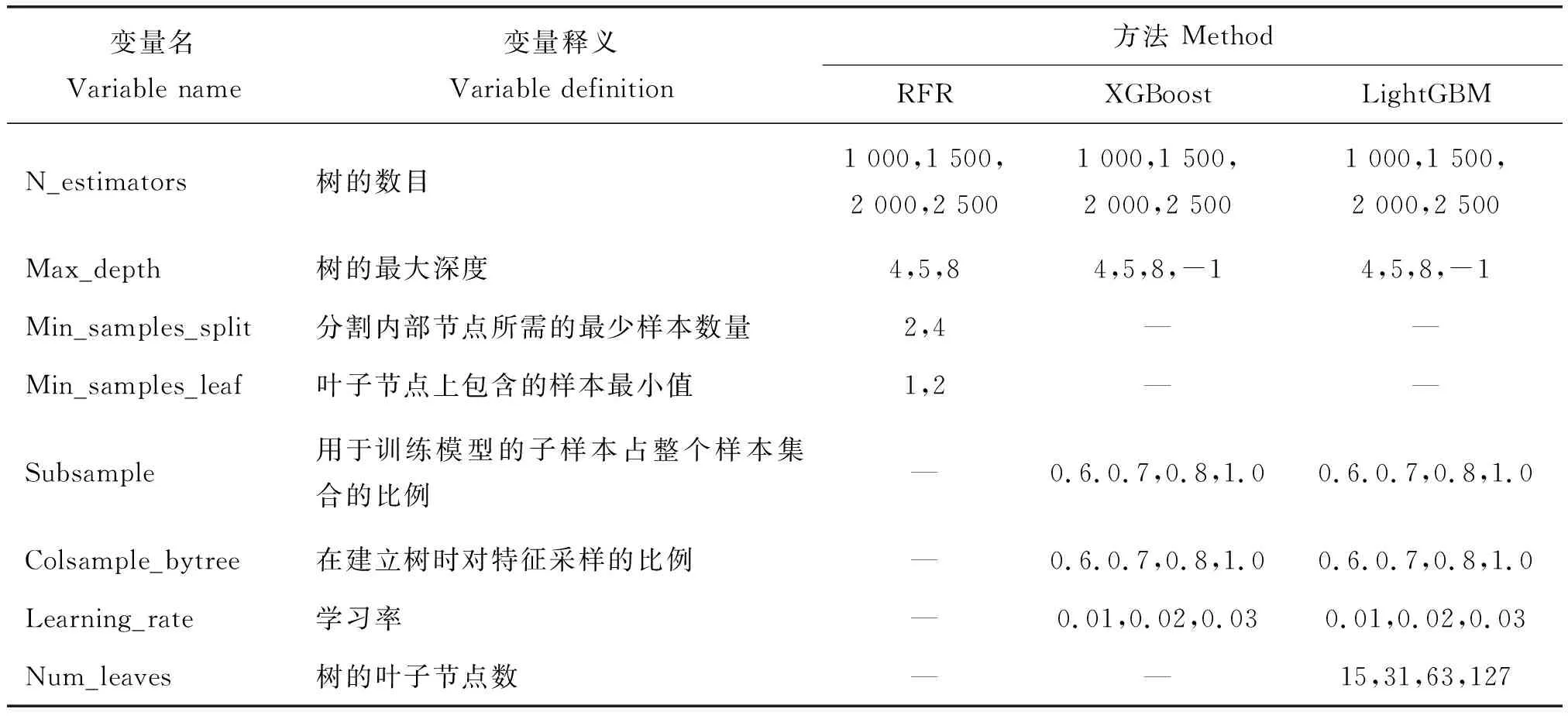
表1 3种机器学习模型网格搜索超参数变量Table 1 Three machine learning models for the grid search of hyper parametric variables

1.3.2神经网络方法

1)时间卷积网络。时间卷积网络是一种能够处理时间序列数据的网络结构，例如给定输入生猪价格序列x0,x1,…,xn共n+1个价格数据，需要预测输出序列y0,y1,…,yn，关键的约束是预测某个时间点t的输出yt仅能使用该时间点t及以前的输入数据x0,x1,…,xt，即

yt=f(x0,x1,…,xt)

(3)

时间卷积网络在不同的应用场景下有不同的实现方式，韩建胜等[18]提出一种基于双向时间卷积网络的情感分析模型,在中文文本情感分类任务中取得了较好的效果。Li等[19]提出了一种用于时间动作分割任务的多阶段架构模型，该模型在动作分割任务中的3个经典数据集上取得了较为先进的结果。Yan等[20]将时间卷积网络应用在天气预报研究中，预测结果较其他方法表现良好。本研究TCN试验结合数据集特点从2个方面进行了改进：一是考虑到输入的时间步为4和较深的网络在小数据集上容易出现过拟合现象的原因，从网络结构，即网络深度方向上进行改进。二是考虑到模型训练中如果学习率的参数值固定可能导致在训练迭代后期出现梯度消失或梯度爆炸现象的原因，从学习率设置，即从学习率动态变化角度进行改进。经过大量试验发现网络深度过大会导致过拟合,学习率固定在迭代轮次较大情况下会出现梯度爆炸。最终本研究具体改进的时间卷积网络(TCN)扩张因果卷积结构如图2所示,输入与输出之间有4个隐藏层，膨胀系数是2的指数次方，即1,2,4,8,16。模型训练时学习率采用动态衰减策略。

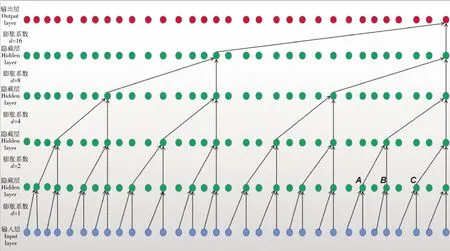
表示输入层节点；表示隐藏层节点；表示输出层节点。 膨胀系数d=n+1，其中n指每层相邻的2个尾端之间的节点数，例如图中A,B,C三点为相邻的尾端，A与B之间的节点数为1，B与C之间的节点数也为1，所以如图中第2隐藏层所示，d=1+1=2。 refers to input layer node; refers to hidden layer node; refers to output layer node Dilation： d=n+1， n refers to the number of nodes between two adjacent end of each layer. For example, the three points A, B and C in the figure are the adjacent end, the number of nodes between A and B is 1, and the number of nodes between B and C is also 1. Therefore, as shown in the second hidden layer in the figure, d=1+1=2.图2 时间卷积网络扩张因果卷积结构图Fig.2 TCN dilated causal convolution structure diagram

2)因果卷积[21]。从直观上，因果卷积类似于将卷积运算劈去一半，令其只能对过去时间步的输入进行运算。在具体网络结构实现上，一维的因果卷积主要通过padding实现，二维的因果卷积主要通过mask filter map实现。如果需要考虑较长时间前的输入变量就必须增加卷积层数，卷积层数的增加就带来了梯度消失、训练复杂、拟合效果不好等问题，为了解决这个问题，需要引入扩张卷积[22]。

3)扩张卷积。扩张卷积的主要作用是在不增加参数和模型复杂度的情况下，可以指数倍的扩大视野。对于因果卷积，为使卷积的感受野变大获得长期依赖，使用扩张卷积作为因果卷积的基本结构。扩张卷积是通过跳过部分输入使filter可以应用于大于filter本身长度的区域,等同于通过增加零来从原始filter中生成更大的filter。

4)残差连接[23]。残差连接在一定程度上消除了深度网络部分梯度消失和爆炸的影响，并且被证明是训练深层网络的有效方法，可使得网络以跨层的方式传递信息。残差结构将输出o表述为输入x和输入的一个非线性变换f(x)的线性叠加：

o=x+f(x)

(4)

1.4 评价指标

本研究试验采用的评价指标为回归问题中的常用3种评价指标，分别为均方误差(MSE)、平均绝对误差(MAE)、决定系数(R2)。均方误差(MSE)是指参数估计值与参数真值之差平方的期望值：

(5)

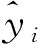
(6)

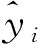
(7)

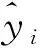
2 结果与讨论

2.1 机器学习模型结果

3种机器学习模型网格搜索后最佳超参数变量见表2。随机森林回归(RFR)模型预测的91个生猪价格数据和真实标签值拟合见图3(a)，预测值与真实标签值基本重合，但第55～60样本段预测效果较差。极端梯度提升(XGBoost)模型的预测值折线趋势基本与真实标签值折线趋势重合，但第55～60样本段预测折线较真实标签值折线略微突出(图3(b))。轻型梯度提升机(LightGBM)模型的第50～55样本段预测值与真实标签值偏差较大，预测值折线较真实标签值折线向下突出，第55～60样本段预测效果也比较差(图3(c))。

综上，3种机器学习模型的预测值折线趋势与真实标签值折线趋势基本一致，其中极端梯度提升(XGBoost)模型预测效果更好。

表2 3种机器学习模型最佳变量取值Table 2 Optimal variable values list of three machine learning models

2.2 神经网络模型结果

经过大量试验发现，在时间卷积网络(TCN)的损失函数为mse、迭代次数为2 000、学习率初始为0.01，每迭代500次学习率衰减一半,结构为4个隐藏层，每个隐藏层节点数为3，卷积核尺寸为2，丢弃率为0.2的情况下，取得了较为出色的预测效果。预测值与真实标签值的趋势拟合见图4，预测值折线趋势基本上与真实标签值折线趋势重合，预测值与真实标签值偏差非常小。预测值与真实标签值的线性拟合公式为：

y=x+0.15

(8)

式中：y为预测值；x为真实标签值。图5示出时间卷积网络模型预测结果与真实值线性拟合结果，可见散点数据基本在直线y=x上，零星几个散点偏离，但偏差较小。

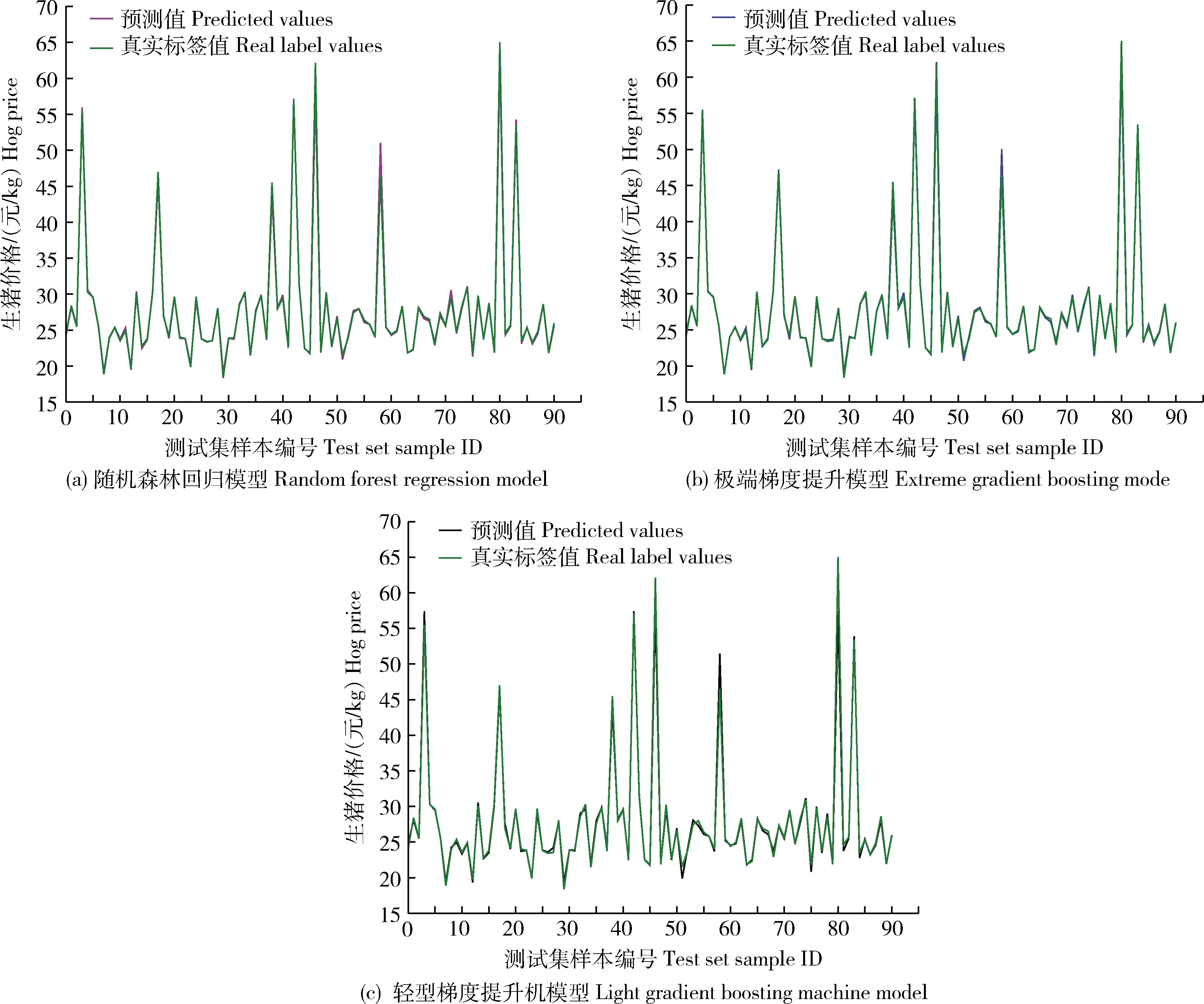
图3 3种机器学习模型对生猪价格的预测结果与真实标签值的拟合Fig.3 Fitting of prediction results of three machine learning models for hog prices with real label values

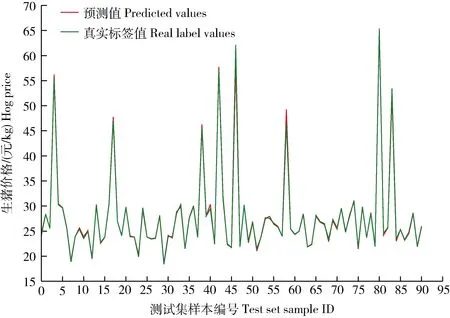
图4 时间卷积网络模型Fig.4 Temporal convolutional network model

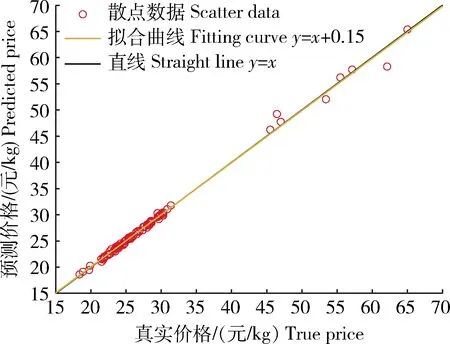
图5 时间卷积网络模型预测结果与真实值线性拟合Fig.5 Linear fitting of prediction results and real value of temporal convolutional network model

2.3 讨论

本研究4种模型预测结果与真实标签值的回归评价指标结果见表3。可知，TCN模型预测结果的MSE为0.340 606，MAE为0.288 424，R2为0.995 683，均优于其他3种机器学习模型结果,且与传统机器学习模型中预测效果最好的XGBoost预测结果(MSE为0.460 842，MAE为0.315 601，R2为0.994 159)比较，3个指标分别提升了26%、8%和0.15%。对比结果表明，TCN相比传统机器学习模型，更加充分地学习到生猪价格之间的非线性变化规律。

表3 4种模型指标结果对比Table 3 Comparison Table of four model index results

3 结 论

本研究针对生猪价格数据具有非线性、突变性、非平稳性的特点，将时间卷积网络(TCN)模型应用于生猪价格预测研究中。结合实际的生猪价格数据，调整改进网络结构及参数，进行大量试验，并同其他3种机器学习模型比较，得到如下结论：

1)从曲线拟合程度和3个评估指标的对比结果看，调优改进后的时间卷积网络模型(TCN)充分地学习生猪价格之间的非线性关系，同机器学习模型预测结果比较，预测效果更优。

2)本研究所采用的时间卷积网络(TCN)模型是高效的时间序列预测算法，在处理大批量数据时，预测效果更为明显，为具有更大数据量的农产品价格预测研究提供了一种思路。