基于局部中心度量的边界点划分密度聚类算法*
2021-12-23张梅,陈梅,李明
张 梅,陈 梅,李 明
(兰州交通大学电子与信息工程学院,甘肃 兰州 730070)
1 引言
在科学研究中,人们希望在无任何先验知识的情况下挖掘出数据内部潜在的特性,而聚类分析技术正好解决了这一问题[1]。聚类分析是一种无监督的学习方式,通过簇内数据间相似性高、簇间数据相似性低的原则来发现数据点在数据集中的真实分布[2]。
目前已有多种聚类算法被提出[3]。k-Means[4]和k-Mediods[5]算法是2种典型的基于划分的算法。该类算法通常需要用户提前输入簇个数,通过迭代使得簇内误差平方和最小来获得最终划分结果,因此基于划分的方法只能识别球状簇。基于密度的噪声应用空间聚类DBSCAN(Density-Based Spatial Clustering of Applications with Noise)[6]能够在具有噪声的数据中将高密度区域划分成簇,但不同参数组合对最终聚类效果影响很大;OPTICS (Ordering Points To Identify the Clustering Structure)[7]会生成一个增广的有序序列簇,不同密度对应不同簇划分结果,虽然参数选取较容易,但由于其实现涉及到二叉树,生成的又是增广序列,因此计算量较大、速度较慢。Chamelon算法[8]是典型的层次聚类算法,它采用动态模型来确定簇之间的相似性,虽然算法发现子簇的能力很强,但时间复杂度相对较高。网格聚类算法中较有代表性的是STING算法[9],此算法虽适合大数据集,但对数据维度的可伸缩性较差,网格划分过细时,计算复杂度较高。
近几年来,为了能识别任意形状、任意密度的簇,聚类研究领域学者们相继提出了新的聚类算法[10 -12]。CLASP 算法[13]借鉴了基于划分和基于层次的方法,使用k-Means获取簇代表点,并根据互k近邻相似性度量进行聚类,但输入参数过多。CFDP(Clustering by Fast search and find of Density Peaks)算法[14]巧妙地将基于密度和基于划分的方法相结合,它认为簇中心点的密度大,与其他密度更大的数据点间的“距离”相对更远。算法可使用决策图来选定聚类中心点,但它不能识别含有多个中心点构成的簇。MulSim(a novel Similar-to-Multiple-point clustering algorithm)算法[15]考虑了单点和多点之间的相似原则,它认为当前点与另一点相似,同时也和该点的多个邻居相似,那么这2点就会被分配到同一簇中。这种方式通过更为严格的条件限制,进一步保证了算法能够有效地发现任意形状、任意密度的簇。由以上分析可知基于密度的聚类算法对任意簇的数据集识别效果更好,因此本文将在密度算法的基础上进行研究。
上述密度聚类算法存在输入参数过多、参数选取敏感及迭代次数过多等缺点。为解决这类问题,本文提出基于局部中心度量的边界点划分密度聚类DBLCM(Density clustering algorithm of Boundary point division based on Local Center Measure)算法。该算法更侧重考虑数据点的不同分布,克服以数据点局部密度作为局部中心度量的缺陷,如局部密度阈值较难给定、不同数据集中各簇的密度不均匀以及使用静态密度设置方式难以识别数据集的真实分布[16]等问题。由于数据分布往往和数据点间的距离正相关,因此本文选用数据点对距离来充当局部中心度量,同时定义了基于互近邻信息弥补的双向绝对距离。根据双向绝对距离与局部中心度量,数据点被划分到核心区域或边界区域。然后,将核心区域的点与它的互近邻中高密度点合并形成初始簇。接着,将边界区域的点加入到其最近邻点所在的初始簇,得到最终簇。本文所提算法属于非启发式算法,无需迭代,输入参数易确定,能识别任意簇,从而反映数据集的真实分布。
2 基于局部中心度量的边界点划分密度聚类算法
一般而言,核心区域的点具有较高的局部密度值,而边界区域的点往往具有较低的局部密度值[16]。本文从距离角度出发提出DBLCM算法,定义数据点对的距离作为局部中心度量,以包含双向信息的互近邻距离来定义新的距离函数。
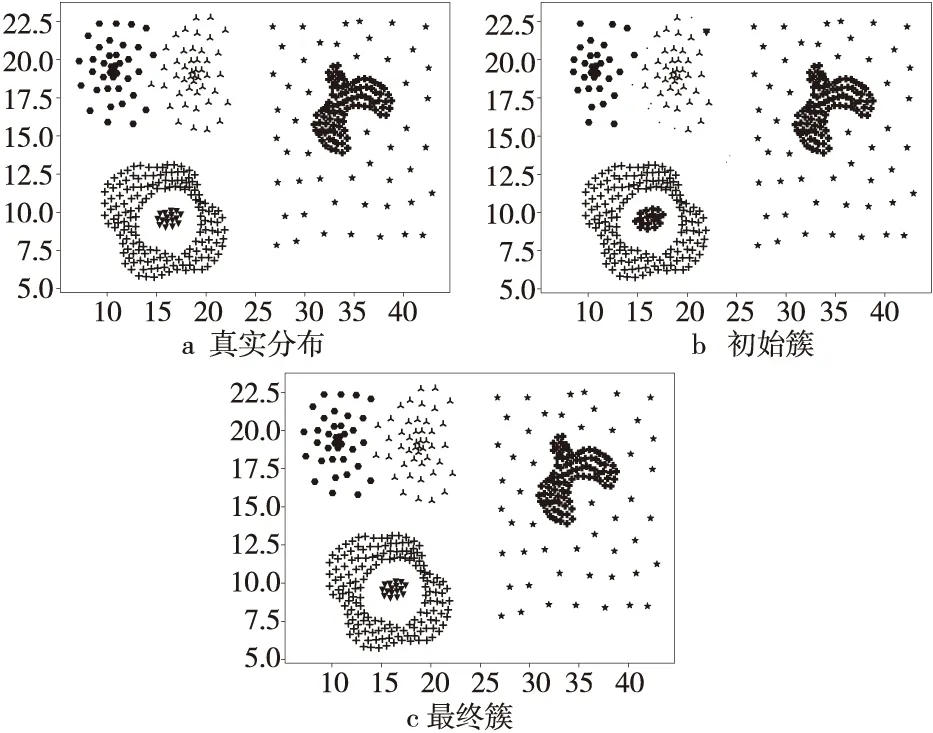
Figure 1 Clustering results of DBLCM algorithm图1 DBLCM算法聚类结果示例
DBLCM通过3个主要阶段得到正确的簇结构,以Compound数据集为例,3个阶段产生的簇如图1所示。
第1阶段在局部中心度量原则下,根据数据点的不同分布将其划分到核心区域或边界区域。第2阶段对核心区域内的点进行分配,每个数据点寻找互近邻中距离最近且密度比其大的点进行合并。图1b展示了核心区域点成簇的结果。该阶段,DBLCM已将大部分点识别出来,直接决定了算法形成的初始簇的准确性。第3阶段,对处于边界区域内的未标记点再进行分配,分配方式为寻找互近邻中最近大密度点所在簇进行分配。本阶段结束后,DBLCM获得了最终的簇结构,如图1c所示。算法结束,可以对比图1a中数据集的真实分布,DBLCM除左上角相接的2个簇的边界部分中的一个点划分错误外,其他点都准确识别。
同一个参数k值对应的互近邻集合是唯一的,“距离+密度”的寻找方式无疑确定了被寻找点的唯一互近邻,因此形成的初始簇是稳定不变的。后期边界点只需要间接寻找互近邻中最近邻点所在的簇合并即可。同一参数k下无论算法运行多少次,初始簇的结构都保持不变。
2.1 相关定义
为了方便后文描述清晰,将本文涉及到的符号定义总结如表1所示。

Table 1 Definition of commonly used symbols in DBLCM algorithm表1 DBLCM算法中常用符号定义
定义1(数据集D) 聚类是通过发掘内部潜在的结构将原始数据集划分为不同子集的过程。在本文中,数据集D定义为:D={x1,x2,…,xi,…,xn},xi表示数据集D中的第i个点,n为数据集中点的个数。
定义2(k-近邻) 在数据集D中,按照欧氏距离将点的邻居由近到远排序,顺序排在前k位的点被称为xi的k-近邻,记为Nk(xi),Nk(xi)⊆D。
定义3(互k-近邻) 在数据集D中,存在2点xi和xj,若xi在xj的k-近邻集合中,同时xj也在xi的k-近邻集合中,这时称xi和xj互为k-近邻,否则不存在互k-近邻关系。xi的互k-近邻,记为MNk(xi)。
定义4(点的局部密度) 数据集中点的局部密度与该点周围的邻居个数有关,本文采用式(1)计算数据点的局部密度。
(1)
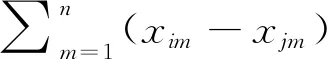
定义5(点的距离) 数据点间的距离反映了数据分布的稀疏程度,本文新定义了基于互k-近邻的双向绝对距离度量方式,如式(2)所示:
Di=DHi-DLi
(2)
其中,Di表示点xi的新距离,DHi表示点xi与其互k-近邻中距离最近且密度比其大的点之间的欧氏距离,DLi表示点xi与其互k-近邻中距离最近且密度比其小的点之间的欧氏距离。很明显,单一考虑2点之间的绝对距离不能适应各类不同数据的动态变化,而基于互k-近邻的双向距离度量方式本质上计算的是以该点为中心,合并其他数据点所能达到的有效范围。
2.2 DBLCM聚类过程
DBLCM算法需要一个输入参数,即点的近邻个数k。算法主要通过3个阶段来实现对数据集中簇的准确识别。首先计算数据点的局部密度和距离;接着根据局部中心度量原则划分核心区域和边界区域,核心区域的点形成初始簇;最后将边界区域中的未标记的点进行分配形成最终簇。算法流程如算法1所示。
算法1基于局部中心度量的边界点划分密度聚类算法DBLCM
输入:数据集D,近邻个数k。
输出:最终簇结构cluster。
步骤1使用k-d树获得数据集D中所有点的k-近邻矩阵。
步骤2在k-近邻矩阵的基础上获得数据集D的互近邻集合M。
步骤3根据不同数据集分布的特点得到局部中心度量阈值,使用式(1)计算所有点的局部密度ρi,追加到局部密度ρ集合中。
步骤4利用式(2)获得所有点的绝对距离,并将其追加到点距离集合point_dist中。
步骤5遍历point_dist,判断集合中每个点的双向绝对距离与局部中心度量阈值MD的关系,若point_disti 步骤5.1进入核心区域的点需要寻找互近邻中距离它最近且密度比它大的数据点成簇,得到初始簇的正确划分结果; 步骤5.2边界区域的点进入待分配点集合unassign_cluster中; 步骤6对待分配点集合unassign_cluster中的点判断其互k-近邻中距离最近点与阈值的关系,确认该点是离群点还是簇内的边界点,继而添加到初始簇中,得到最终簇结构cluster; 步骤7算法结束。 以上6个步骤执行完成之后,可得到对应数据集的最终簇结构。算法整个分配过程按步骤顺序执行,当数据集中的所有点被分配结束(即所有点都分配了类标),算法就会自动停止,无需人为输入停止迭代的参数。 DBLCM在初始阶段首先借助k-近邻矩阵来获得互k-近邻集合,步骤2中根据定义3判断数据集中的每个点xi以及邻居xj是否满足互k-近邻关系,满足条件则将xj添加至xi的互k-近邻集合保存,否则扫描下一个数据点,直到所有点访问结束。步骤3计算点的局部密度和距离,其中式(1)用来计算每个数据点的局部密度ρi,对于点xi,若该点与其邻居xj的欧氏距离小于阈值MD,可认为xj为xi的有效邻居,反之xi的邻居中不统计xj。其中,MD为设定的局部中心度量阈值,通过计算数据点对欧氏距离(不包含点自身的距离),整体升序排序后取所有距离总数的0.02位次位置对应值作为固定值赋予MD。步骤4利用式(2)计算每个点xi的新的绝对距离point_disti,在步骤2存储的互k-近邻列表中分别寻找比点xi密度大且离xi最近的邻居xj,计算xi与xj的距离,寻找比点xi密度小且离其最近的邻居xs,计算xi与xs的距离。 步骤5中,对于每个点xi,若绝对距离小于阈值MD,则认为该点处于核心区域;反之则认为该点处于边界区域,将其添加到待分配簇中。对处于核心区域的点,依次遍历,将点xi添加到其互k-近邻中距离最近且密度比它大的邻居点所在的簇。直到核心区域中的数据点遍历结束,至此形成初始簇。 步骤6中,为了区分待分配簇中的点是属于簇内的边界点还是离群点,算法采用间接判断点xi的互k-近邻中与其距离最近点的距离和阈值MD大小的方式,若点xi近邻点的距离小于MD,表明该点分布在离簇较稀疏的部分,但仍属于簇内的有效点,因此将点xi分配给近邻点所在的簇;反之将点xi视为离群点,直接更新点xi的类标值为-2。 为了评估DBLCM算法的有效性,本节将DBLCM与3个经典算法和3个近几年聚类领域学者新提出的优秀算法,在包含任意形状、任意密度的二维数据集及多维数据集上进行实验对比。其中二维数据集的规模不大,方便采用可视化图形展示方式对聚类效果进行呈现。为了在同一标准上更好地展示算法的性能,本文采用ARI(Adjusted Rand Index)和NMI(Normalized Mutual Information)2个外部评价指标进行量化评估。另外,本节还对DBLCM中参数k的敏感性、各对比算法的时间复杂度分别进行了分析说明。 实验采用的二维数据集有Aggregation、Compound、Spiral和Toy,其中Toy数据集引用于文献[17],其它的二维数据集均来自于东芬兰大学的网站(http://cs.joensuu.fi/sipu/datasets/)。数据集包含球状簇、螺旋簇、均匀密度簇和不均匀密度簇,能分别代表数据点的各种复杂分布。采用的多维数据集有Glass、Iris、Leaf和SPECTF,均来自UCI网站(http://archive.ics.uci.edu/ml/datasets.html)。各数据集的具体信息如表2所示。 Table 2 Information descriptions of datasets 表2 数据集信息说明 本节将使用3个经典算法和3个优秀的新算法作为对比算法,其中DBLCM算法的代码用Python语言实现,k-Means[4]和DBSCAN算法[6]均来自“scikit-learn”(http://scikit-learn.org/stable/index.html)库中,OPTICS算法[7]代码来自GitHub,CLASP[13]、CFDP[14]和MulSim[15]代码均由论文作者提供。 Figure 2 Clustering results of DBLCM and the contrast algorithms on the Aggregation dataset图2 DBLCM与对比算法在Aggregation 数据集上的聚类结果 DBLCM算法及各对比算法具体参数如表3所示。 Table 3 Parameters description of the algorithms 表3 DBLCM算法及各对比算法参数 3.4.1 二维数据集上的结果分析说明 (1)Aggregation数据集。 Aggregation是一个球状簇数据集,该数据集的簇内密度比较均匀。聚类难点在于每个簇的大小不一,且数据集中的4个簇两两之间通过几点连线的方式连接在一起。图2所示为DBLCM与6个对比算法在该数据集上的可视化结果。其中图2a为Aggregation的真实分布图,图2b~图2h为6个对比算法的聚类结果图。 从图2 可以看出,在Aggregation数据集上,DBLCM和CFDP算法均准确识别出了簇的真实结构,其中DBLCM算法采用了恰当的局部中心度量值,划分的核心区域的点遵循互近邻一致性原则聚类,保证了在初始簇的寻找阶段就将4个簇的连接部分划分开来,解决了识别的难点。而k-Means算法受初始聚类中心的影响,识别出7个球状簇,破坏了原簇的真实结构。DBSCAN算法采用静态密度设置方式,左上角簇中处于边缘的点没有正确识别,同时右边的2个簇的中间衔接部分也没有断开。OPTICS算法对识别的效果虽然相对DBSCAN有所改进,但边界区域仍有几个点错分。CLASP算法因借鉴k-Means来选取初始中心点,造成了左上角簇被划分为2个小簇,因此结果也一般。MulSim算法除右边2个簇连接部分的2个数据点被识别错外,其他点均正确识别,较完美地解决了该数据集的识别难点。 Figure 3 Clustering results of DBLCM and the contrast algorithms on the Compound dataset图3 DBLCM与对比算法在Compound 数据集上的聚类结果 (2)Compound数据集。 Compound数据集是不均匀密度的簇,识别的难点在于每个簇密度分布不一,同时包含多个中心点形成的簇。图3所示为DBLCM与6个对比算法在该数据集上的可视化结果,其中图3a为Compound的真实分布图,图3b~图3h为6个对比算法的聚类结果图。 从图3可以看出,在Compound数据集上,DBLCM相较于真实分布只错误划分了左上角2个簇间边界的一个衔接点,识别效果优于其他对比算法。而k-Means算法将左下角和右边包含2个中心点的簇划分成左右各半。CFDP算法受其思想的限制,没有正确识别出包含2个中心点的簇。DBSCAN和OPTICS算法均因为静态密度的设置在该数据集上的聚类遇到了困难。CLASP算法也没有将右边的簇正确识别出来。MulSim算法除2个簇中的几个边界点识别错误外,其余部分均正确识别了,较大程度上解决了数据集的识别难点。 (3)Spiral数据集。 Spiral数据集中的簇呈螺旋型的分布,密度随螺旋的方向不一。图4所示为DBLCM与6个对比算法在该数据集上的可视化结果,其中图4a为Spiral的真实分布图,图4b~图4h为6个对比算法的聚类结果图。 Figure 4 Clustering results of DBLCM and the contrast algorithms on the Spiral dataset图4 DBLCM与对比算法在Spiral 数据集上的聚类结果 从图4可以看出,在Spiral数据集上,DBLCM、DBSCAN、CFDP和MulSim均正确识别出了真实的簇结构。而k-Means、CLASP 2种算法只考虑了数据点间的绝对距离和基于单个中心点的聚类方式而导致识别效果很差。OPTICS算法受密度设置的影响只对密度大的点正确识别了,大多数点被识别为异常点。 (4)Toy数据集。 Toy是具有2个中心点的数据集。图5所示为DBLCM与6个对比算法在该数据集上的可视化结果,其中图5a为Toy的真实分布图,图5b~图5h为6个对比算法的聚类结果图。 从图5可以看出,在Toy数据集上,DBLCM、DBSCAN、CLASP和MulSim均正确识别出了真实的簇结构。而k-Means和CFDP将原簇划分为了左右2个簇,没有识别出簇的主要部分,原因在于它们都只是基于一个中心点的思想进行聚类,从而对该类基于多个中心点的数据集基本无效。OPTICS算法除了在静态密度的限制下将内部簇的边界点划分为离群点外,也识别出了基本正确的簇结构。 表4统计了DBLCM与对比算法在二维数据集上的指标量化结果。从表4的统计结果看出,DBLCM性能整体优于对比算法,评价指标准确反映了DBLCM能对数据集进行真实划分。 图2~图5从可视化的角度展示了DBLCM和6个对比算法在二维数据集上的聚类结果。为了更加直观地突出DBLCM算法相较于其他算法的优势,图6采用直方图的方式来展现。 Table 4 Quantitative results on two-dimensional datasets表4 二维数据集上指标量化结果 从图6a和图6b 2幅图可以观察到,DBLCM算法在本文使用的4个二维数据集上的2项指标均高于其他算法的对应指标,这也表明了DBLCM识别到的最终簇的质量高,算法整体优于其他算法。 3.4.2 多维数据集结果分析说明 为了测试DBLCM在多维度数据集上的聚类效果,本节选用Glass、Iris、Leaf和SPECTF 4个多维数据集(http://cs.joensuu.fi/sipu/datasets/)进行实验。考虑到多维数据集对应的不同维数属性的量级不一致,实验中对数据集的每一维做了Z-score标准化处理。聚类最终效果采用直方图方式来分析性能优劣。 表5中统计了DBLCM和对比算法在4个多维数据集上的量化结果。图7a和图7b采用直方图的方式,说明DBLCM算法在Glass、Iris和Leaf 3个数据集上ARI和NMI指标排名都高于对比算法。而在数据集SPECTF上,虽然DBSCAN算法具有排名最高的NMI指标,但ARI指标值为0,该情况下算法的划分结果是无效的。纵观其他算法在SPECTF数据集上的表现,DBLCM算法在SPECTF上仅次于MulSim算法,具有次优ARI和NMI结果。 Figure 6 Index histogram of DBLCM and the contrast algorithms on two-dimensional datasets图6 DBLCM与对比算法在二维数据集上的评价指标直方图 Table 5 Quantitative results on multi-dimensional datasets表5 多维数据集上指标量化结果 Figure 7 Index histogram of DBLCM and the contrast algorithms on multi-dimensional datasets图7 DBLCM与对比算法在多维数据集上的评价指标直方图 各对比算法的参数通过大量的实验寻优获得,不同数据集适用参数汇总如表6所示。 最后,为显示算法在不同维度、任意密度、任意簇的数据集上的综合性能,绘制了DBLCM在8个数据集上的NMI量化指标箱线图,如图8所示。图8中各对比算法对应的箱线图有以下特征:〇表示温和的异常值,即和正常数据偏差较小;黑色箱体的上下边界分别表示数据分布中的上下四分位数,箱体的中间白色虚线表示数据分布中的中位数;箱体上下两端的短横线表示数据分布中最大值与最小值。 从图8所示箱线图中可以看出,DBLCM算法对应的各项特征所处的位置都高于其他算法的特征的,说明本文算法在8个数据集上的值相对稳定,综合聚类性能优于其他对比算法。 综上所述,DBLCM算法在局部中心度量原则下,达到了高效识别任意簇的目的,和其他对比算法相比,DBLCM更具鲁棒性。 Table 6 Parameter statistics of DBLCM and the contrast algorithms on datasets表6 DBLCM及对比算法在数据集上的参数统计 Figure 8 NMI indicators of DBLCM on 8 datasets图8 DBLCM在8个数据集上NMI指标 本节测试DBLCM对输入参数k(近邻个数)的敏感性。实验用到前文的8个数据集,通过更改k值来记录聚类后簇的质量。 由于DBLCM在形成初始簇阶段采用互k-近邻吸引的方式,因此合适的k值直接决定着聚类后簇的质量。本节根据表6中DBLCM在各数据集上能取得的最优结果对应的参数k范围绘制了图9。从图9可以看出,随着k的增长,挖掘到的各数据集的簇的质量在逐渐变高。同时也发现,当k值为5时,绝大多数数据集评价指标均能达到最优指标的95%,当k大于5后,评价指标值随k值增大逐渐稳定,变化幅度不大。以上分析说明DBLCM对参数k不敏感。 Figure 9 Sensitivity test of parameter k for DBLCM algorithm图9 DBLCM算法中参数k的敏感性测试 DBLCM算法首先使用k-d树[18]来构建k-近邻矩阵,时间复杂度为O(n·logn),n代表数据集D中点的数目。然后寻找互近邻和计算点的局部密度均花费O(n·k),其中k代表最近邻个数。3个步骤对应时间复杂度可近似记为O(n·logn)。接着形成初始簇的时间花费为O(n·k)。最后边界区域的点分配的时间花费为O(m·k),其中,m为未分配簇列表中点的个数,通常情况下m≪n,时间复杂度可以忽略不计。因此,DBLCM的总时间复杂度为O(n·logn)。 (1)DBLCM算法有效弥补了静态密度设置方法的缺陷。 经典的密度聚类算法常选用静态密度设置的方式来获得密度阈值,不能得到一个普适的阈值参数。而DBLCM算法考虑了数据集的不同分布,提出了自适应密度的计算方式,将连接紧密但比较稀疏的2个簇成功断开,从而较好地解决了经典聚类算法遇到的密度设置问题。 (2)DBLCM算法有效弥补了单向距离挖掘数据方式的缺陷。 聚类算法例如k-Means、DBSCAN和OPTICS都需要生成一个相似性矩阵,常采用单向距离决定的数据挖掘方式。而DBLCM算法考虑了基于互k-近邻的双向绝对距离方式,本质上计算的是以该点为中心,合并其它数据点所能达到的有效范围。算法前期操作为初始簇的形成奠定了基础,同时也大大提高了初始簇的划分精确度。 (3)DBLCM算法稳定,无需迭代,对参数不敏感,同一参数下结果唯一。 密度聚类算法中不同的参数组合对聚类结果影响大,涉及到误差函数的还需要迭代多次寻优。而DBLCM算法对参数k的选取不敏感,初始簇的形成稳定、质量高,算法无需迭代,同一参数下聚类结果唯一。 为了解决聚类中任意簇检测精确度不高、迭代次数多及效果不佳等缺点,本文提出DBLCM算法。为了验证DBLCM算法的有效性,本文选用了6个有代表性的优秀对比算法在二维数据集及多维数据集上进行了对比实验。另外,为了验证DBLCM算法对参数k的敏感性,在本文使用的8个数据集上均做了测试。实验结果表明,DBLCM算法相较于对比算法具有良好的性能,识别精确度更高,检测任意簇的效果更好,而且对参数k的选取不敏感,算法无需迭代。3 实验与结果分析
3.1 实验数据集说明

3.2 对比算法说明

3.3 DBLCM算法及对比算法的参数

3.4 实验结果及分析




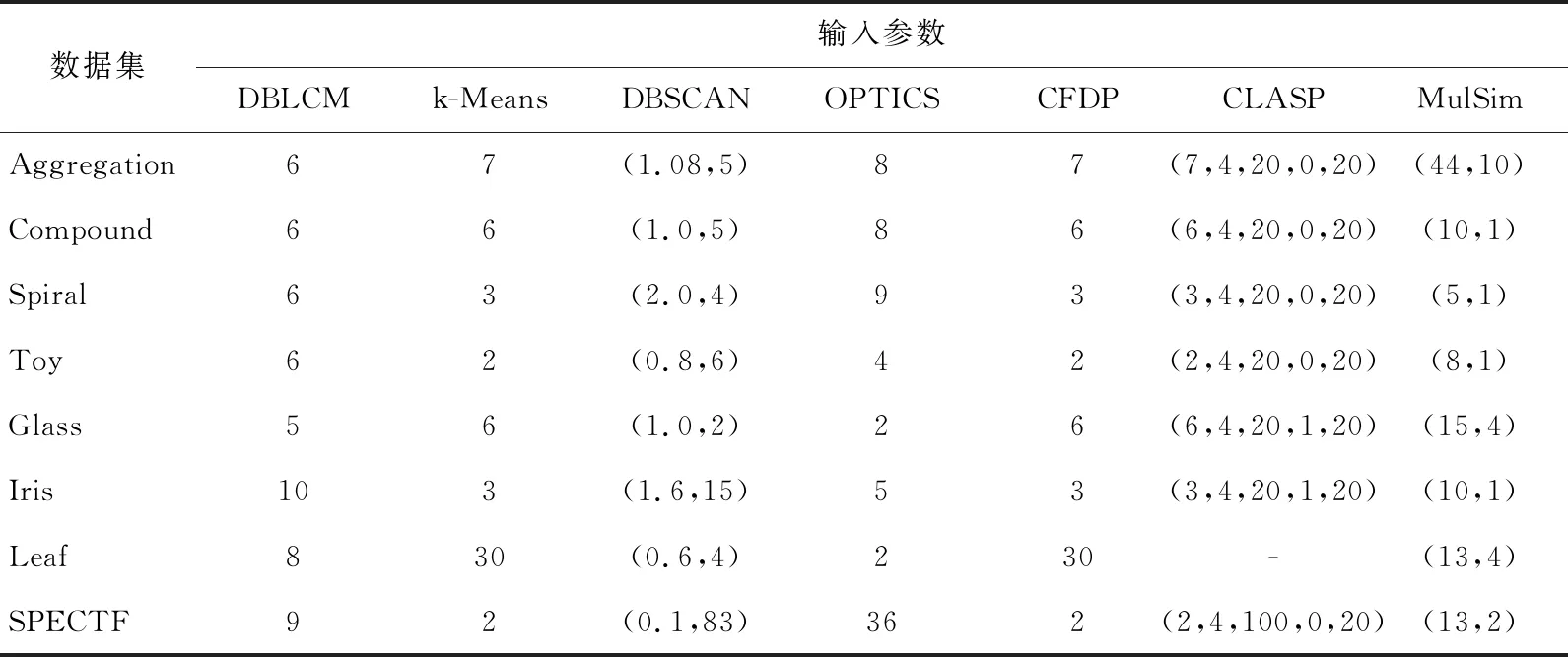
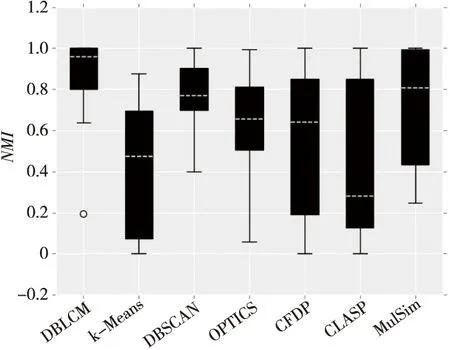
3.5 参数敏感性分析

3.6 DBLCM算法时间复杂度分析
3.7 DBLCM算法特点分析
4 结束语
