基于贝叶斯网络的列控车载设备故障诊断
2021-12-23查园园王亭岭上官伟1b
查园园,王亭岭,上官伟,1b
(1.北京交通大学 a.电子信息工程学院,b.轨道交通控制与安全国家重点实验室,北京 100044;2.华北水利水电大学 电力学院,郑州 450045)
近年来我国高速铁路事业突飞猛进,高铁凭借速度快等特点,成为人们不可或缺的代步工具,而如何确保列车在提速的同时能够安全运行,引起了该领域专家学者的关注.列车运行控制系统是控制高铁列车运行的重要设备,且对于目前应用较为广泛的CTCS3-300T型列车来说,列车运行控制系统车载设备的作用更是重中之重[1].一旦设备发生故障,列车的运行效率和运行安全都会受到一定程度的影响,若不能快速准确地定位到故障原因,甚至会造成一定的经济损失.《十三五交通领域科技创新专项规划》中强调要进一步强化高速铁路体系化安全保障技术,因此,快速、高效地定位列控车载设备的故障点成为研究热潮.
目前,车载设备故障信息基本上都是以文本的形式保存,缺乏统一性和规范性,针对该问题,文献[2]提出了基于文本挖掘的故障诊断方法,利用主题模型进行语义上的文本挖掘,进而得到故障文本在降维空间中的表达,以此来提高列控车载设备的故障诊断正确率.文献[3]在现场技术人员经验知识的基础上,采用Labeled-LDA方法对车载设备故障日志进行特征提取,并通过粒子群优化的支持向量机算法对故障信息进行分类,以提高分类的准确性.文献[4]通过对车载设备故障诊断技术发展现状的分析,针对车载设备故障数据的多样性、复杂性和耦合性,提出基于案例推理的故障诊断方法,首先结合案例特点,利用层次组织方法形成案例库,并在归一化处理后得到每个案例对应的特征属性的权重,其次利用加权K-NN算法进行案例匹配,提高了匹配效率,但过多依赖先验知识.文献[5]构建了无线闭塞中心的故障树模型,来处理由于RBC接口较多而很难快速找到故障原因的问题,并根据实际情况采取不同的措施来保障RBC的安全性. 文献[6]根据超出安全速度/距离有效和驾驶员按照安全速度/距离行驶的监控和保护原则,建立故障树,然后根据一定的对应关系将其转化为CTCS3-300T型车载设备的贝叶斯网络进行故障诊断.文献[7]针对车载设备故障分析过多依赖专家经验的特点,以应答器信息接收模块为研究对象,提出了基于RS-ICS-BP的故障诊断方法,即首先利用粗糙集理论对故障特征进行简约,其次通过改进布谷鸟算法确定BP神经网络的初始权值和阈值,最后利用BP神经网络对故障进行分类.文献[8]考虑到车载设备正常数据与故障数据不均衡的问题,采用代价敏感森林来优化随机森林对故障的分类效果.文献[9]对列车的运行数据实时采集并进行智能分析,结合维修策略构成的规则库实现在线故障诊断的功能.
贝叶斯网络是处理不确定性问题的有效方法之一,在解决故障诊断问题上得到了广泛的应用.文献[10]把贝叶斯网络运用到智能变电站里继电保护器的故障诊断中.文献[11]利用基于贝叶斯网络的数据驱动方法对永磁同步电机的三相逆变器进行故障诊断.文献[12]将贝叶斯网络与一对多支持向量机相结合,对轴承的故障进行诊断.
因此,本文作者针对列控车载设备故障的不确定性、不唯一性、耦合性等特点,利用贝叶斯网络对其进行故障诊断,提高了故障诊断的准确率.
1 基本理论
从列控车载设备的结构出发,对列车动态监测系统DMS所记录的列控车载设备的故障特点进行分析,给出采用贝叶斯网络方法进行故障诊断建模的原因.
1.1 列控车载设备的结构及故障特点
列控车载设备是列车运行控制系统的核心子系统,是保障列车稳定、快速、安全运行的必要设备.目前CTCS-3级列控系统在高速铁路中应用较多,因此本文以CTCS3-300T型(简称“300T型”)列控车载设备为研究对象.300T型车载设备主要由无线通信单元GSM-R、车载安全计算机VC、测速测距单元SDU、轨道电路信息读取器TCR、列车接口单元TIU、应答器信息接收单元BTM、人机界面DMI组成[13],详细结构组成如图1所示.
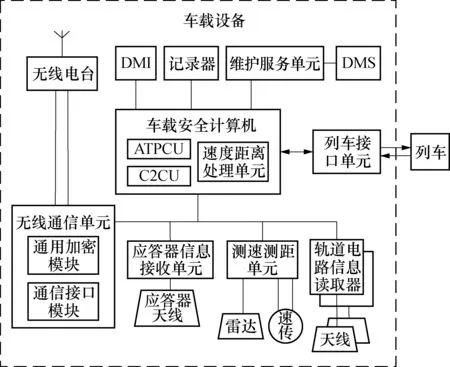
图1 300T型列控车载设备结构组成Fig.1 Structural composition of 300T on-board equipment
根据列控车载设备的结构,结合300T型列控车载设备的典型故障案例[14-15],对列车动态监测系统中的故障记录信息进行分析,从而得出列控车载设备的故障具有不确定性、不唯一性、复杂性、耦合性的特点.
1)不确定性.车载设备的故障与否是一个概率性的问题,存在一定的不确定性.另外,由于运行环境不同、技术人员的工作方式不同,会导致车载设备故障的可能性不同.
2)不唯一性.故障发生所表现出来的故障征兆与故障发生的原因之间并非是一一对应的关系,同一故障征兆可能由不同的故障原因所导致的,同一故障原因也可能造成不同的故障征兆.
3)复杂性.故障的记录方式没有严格的标准,且伴随着下一代列控系统的提出,地面设备车载化成为大势所趋,这也就意味着车载设备的结构会复杂化.
4)耦合性.正是由于车载设备的结构较为复杂,故障的发生存在着一定的连带关系,即当某个部位发生故障时,与其相关联的部位也会发生一定程度上的失效.
1.2 贝叶斯网络的原理
贝叶斯网络的概念在1988年被Pearl所提出,它是基于概率问题的图形化网络,由有向无环图(DAG)和条件概率分布(CPD)两部分构成.其中,有向无环图是对所描述问题具体结构的一个可视化表示,由节点和有向边组成.条件概率分布是对各节点之间内在联系的一个量化表示,而本文所讨论的列控车载设备的贝叶斯网络故障诊断模型的节点是离散型变量,因此条件概率分布可用条件概率表(CPT)来描述.
结构学习是对贝叶斯网络结构的进一步修正,包括基于约束的结构学习和基于评分搜索的结构学习.前者是在数据集的基础上对各节点进行独立性测试,以此来获取节点间的依赖关系.后者的核心是评分函数的确定,它遍历所有可能的贝叶斯网络结构,并利用评分函数对其进行评分,选取分数最高的结构模型.但随着节点数目的增加,其复杂度呈指数形式增长[16],需遍历的DAG的个数为
(1)
式中:n为节点个数.为了避免学习算法的复杂度过高,选取以局部搜索的方式来确定最优网络结构,本文采用K2算法进行结构学习.
参数学习是确定各节点的条件概率表的过程,也是对节点间的依赖强度的界定.参数学习包括在数据结构完整下的极大似然参数估计(Maximum Likelihood Estimation,MLE)和贝叶斯估计(Bayesian estimation),以及在数据结构缺失条件下的期望最大化算法(Expectation-Maximization,EM).
贝叶斯网络的推理是对贝叶斯网络模型的验证过程,包括因果推理、诊断推理和支持推理.因为故障诊断是一个“执果索因”的过程,因此主要用到的是诊断推理.
贝叶斯网络不苛求数据结构的完整、不过度依赖先验知识以及在解决不确定性问题上的独特优势,促使选择它作为本文的核心算法.
2 故障诊断模型的建立
根据理论知识和数据基础,建立一个学习能力强、正确率较高的列控车载设备故障诊断模型,主要步骤如下.
1)通过对列车动态监测系统的故障记录信息进行分析,确定贝叶斯网络的节点信息,获得故障诊断知识库.
2)结合经典故障案例的处理方法,确定各节点之间的依赖关系,建立基于专家知识的贝叶斯网络.
3)利用故障记录数据集进行结构学习和参数学习,包括以车载设备为整体的学习和以各故障部位为整体的学习.
4)通过整合,建立更符合实际问题的最优贝叶斯网络故障诊断模型.
2.1 诊断信息的获取
诊断信息的获取即是根据列控车载设备故障数据集确定贝叶斯网络各节点信息的过程.本文以某高铁站300T型车载设备2018年的322条真实故障数据作为样本数据,故障记录信息一般包括时间、类别、故障描述、处理措施等内容,具体形式如表1所示.

表1 车载设备故障案例Tab.1 On-board equipment fault cases
通过对故障数据的进一步分析,将故障数据信息分为故障原因、故障部位和故障征兆3个层次,按照这3个层次可将表1可转换为如表2所示的数据形式.

表2 故障数据示例Tab.2 Examples of fault data
对列车动态监测系统记录的原始故障数据进行特征提取和整理,得到如表3所示的故障记录信息.在发生故障时,利用表3中的对应关系,也可进行粗略的故障诊断,但其诊断正确率低、可移植性差,不适合运用到实际的运行环境中.如当出现“无线超时、制动、C3转C2”故障征兆时,可能是GSM-R部位发生故障,也可能是车载安全计算机发生故障.这也说明了列控车载设备故障数据的不唯一性、不确定性,因此提出对贝叶斯网络故障诊断方法的研究.
表3中给出了故障部位和故障原因节点的编号,且从中可以看出,不同的故障原因导致的故障征兆之间存在重叠,如“制动”、“停车”故障征兆在多处故障数据中出现,通过对其进行简约可得到如表4所示的故障征兆节点的编号.完成对节点的编号后,对原始故障数据进行处理,以便接下来计算机的读取.
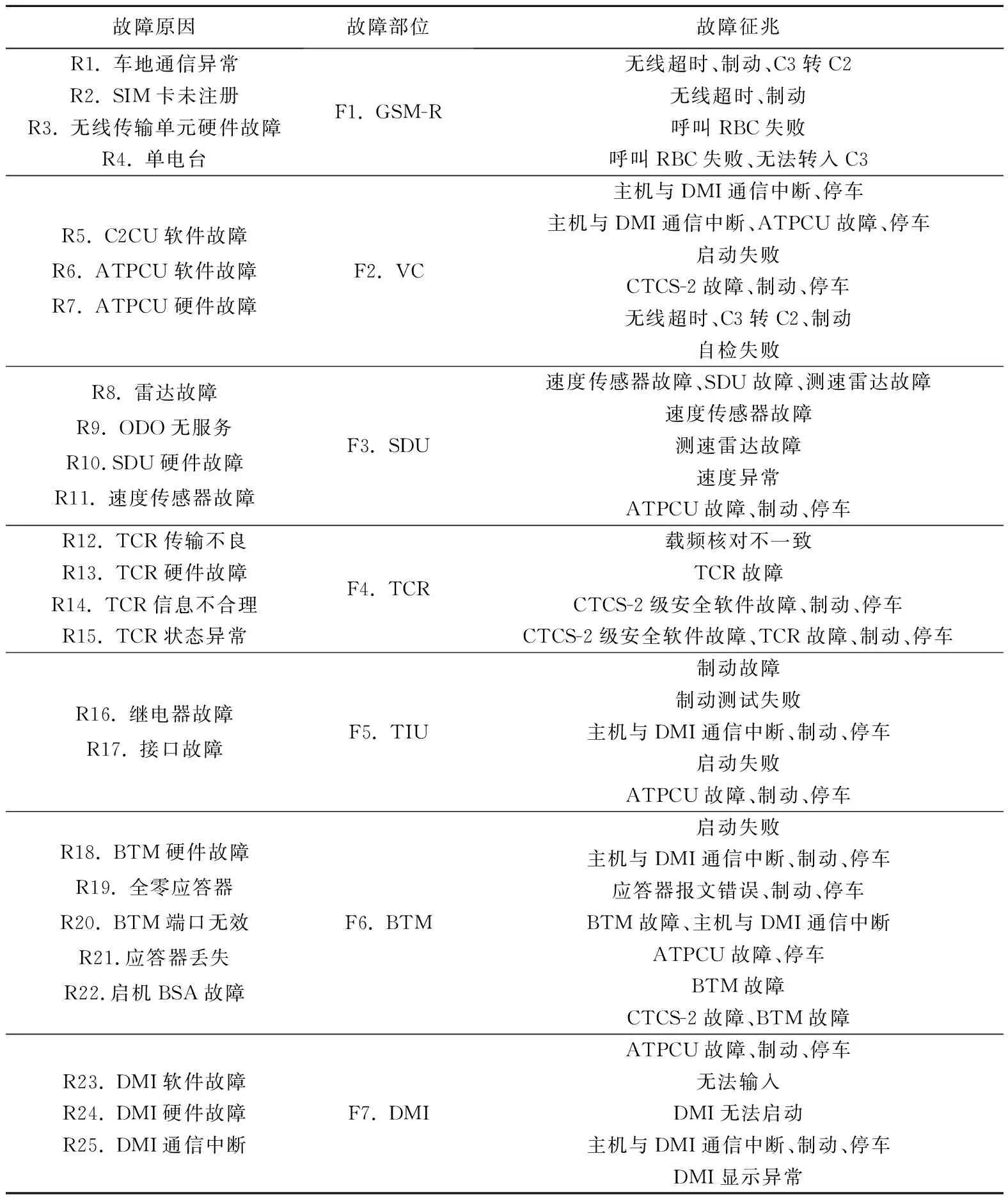
表3 列控车载设备故障信息Tab.3 Fault information of train control on-board equipment
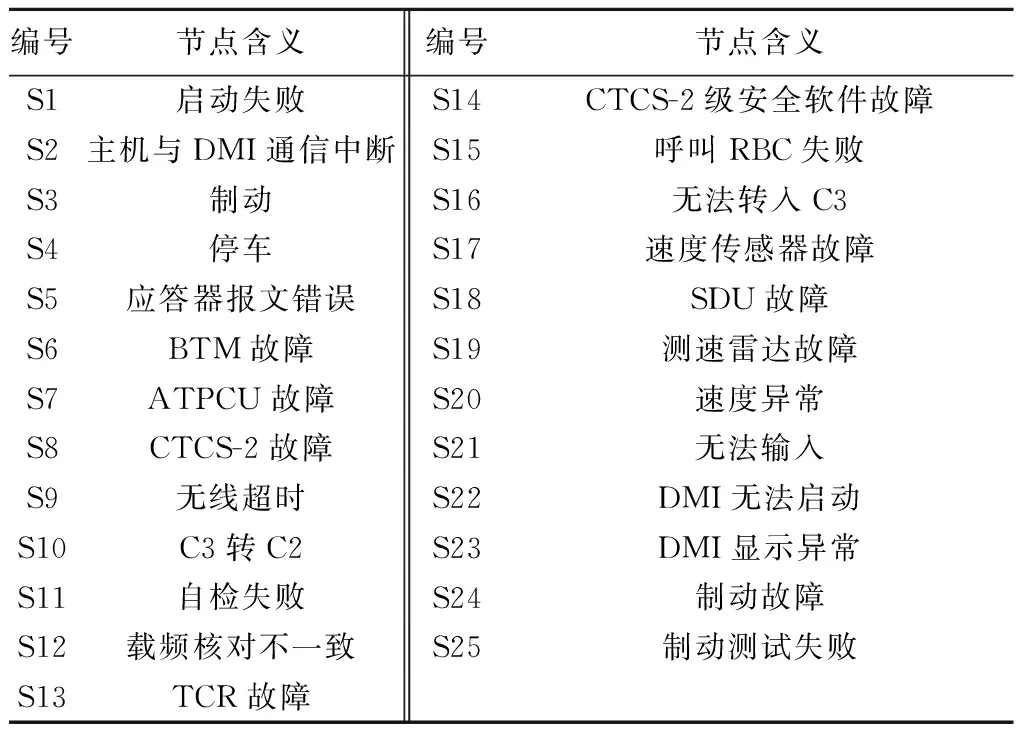
表4 故障征兆节点编号Tab.4 Numbers of nodes with fault signs
2.2 基于专家知识的贝叶斯网络
邻接矩阵表示着贝叶斯网络节点间的依赖关系,矩阵中元素为1表示对应的两个节点之间存在依赖关系,即存在有向边的连接;若为0则表示两节点相互独立.由2.1可知贝叶斯网络由25个故障原因节点、7个故障部位节点和25个故障征兆节点组成,通过分析建立相应的邻接矩阵,便可得到如图2所示的基于专家知识的贝叶斯网络.
2.3 结构学习和参数学习
为了使故障诊断模型更符合实际问题,需要在基于专家知识的贝叶斯网络的基础上进行学习和优化.考虑到复杂度的问题且网络中各节点的顺序是已知的,因此本文选择K2算法进行结构学习.从节点R1开始按顺序遍历,依据评分函数的值获取相应的父节点集合,进而获取故障原因节点和故障征兆节点间的隐藏关系.然后将遍历得到的给定数据集下具有最大后验概率的网络结构作为学习结果.为了得到与实际情况更加吻合的网络结构,分别从故障部位和整个车载设备两个层次进行结构学习,具体的流程图如图3所示.
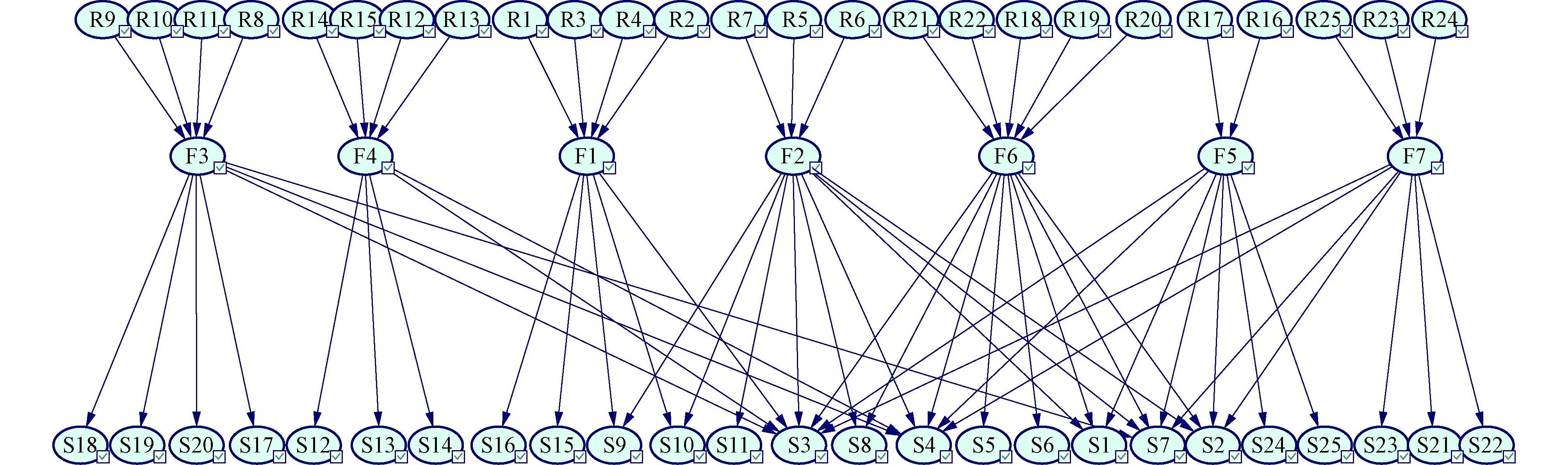
图 2 基于专家知识的贝叶斯网络Fig.2 BN based on expert knowledge
在这里,假设故障原因层、故障部位层和故障征兆层各层次内的节点间是相互独立的.对于学习得到的故障原因层和故障征兆层的依赖关系,若在以各故障部位为整体学习得到的网络和以车载设备为整体学习得到的网络中均存在则给予保留.否则结合专家经验判断是否保留.
在得到最优的贝叶斯网络结构后便可进行参数学习,由于故障数据相对来说是完整的,且模型已知,参数未确定,故本文采用极大似然估计的方法进行参数学习.首先,假设一个确定但未知的参数θ,其次对样本集进行最大似然参数估计.记已知样本集为
D={x1,x2,…,xn}
(2)
则对应的似然函数为
L(θ)=P(x1,x2,…,xn|θ)=
(3)
接着求解使似然函数取得最大值的参数θ,即
(4)
对数似然函数为
(5)
因此,求似然函数最大值的问题就变成了求解对数似然函数最大值的问题,求导解出的最大值对应的参数θ即为参数学习的结果.以故障原因节点R1-R7为例,其参数学习后的结果如表5所示.
2.4 最优贝叶斯网络
通过结构学习得到了给定数据集下具有最大后验概率的网络结构,通过参数学习得到了先验知识下网络中各节点的最优条件概率分布.整理后得到如图4所示的列控车载设备最优贝叶斯网络故障诊断模型.
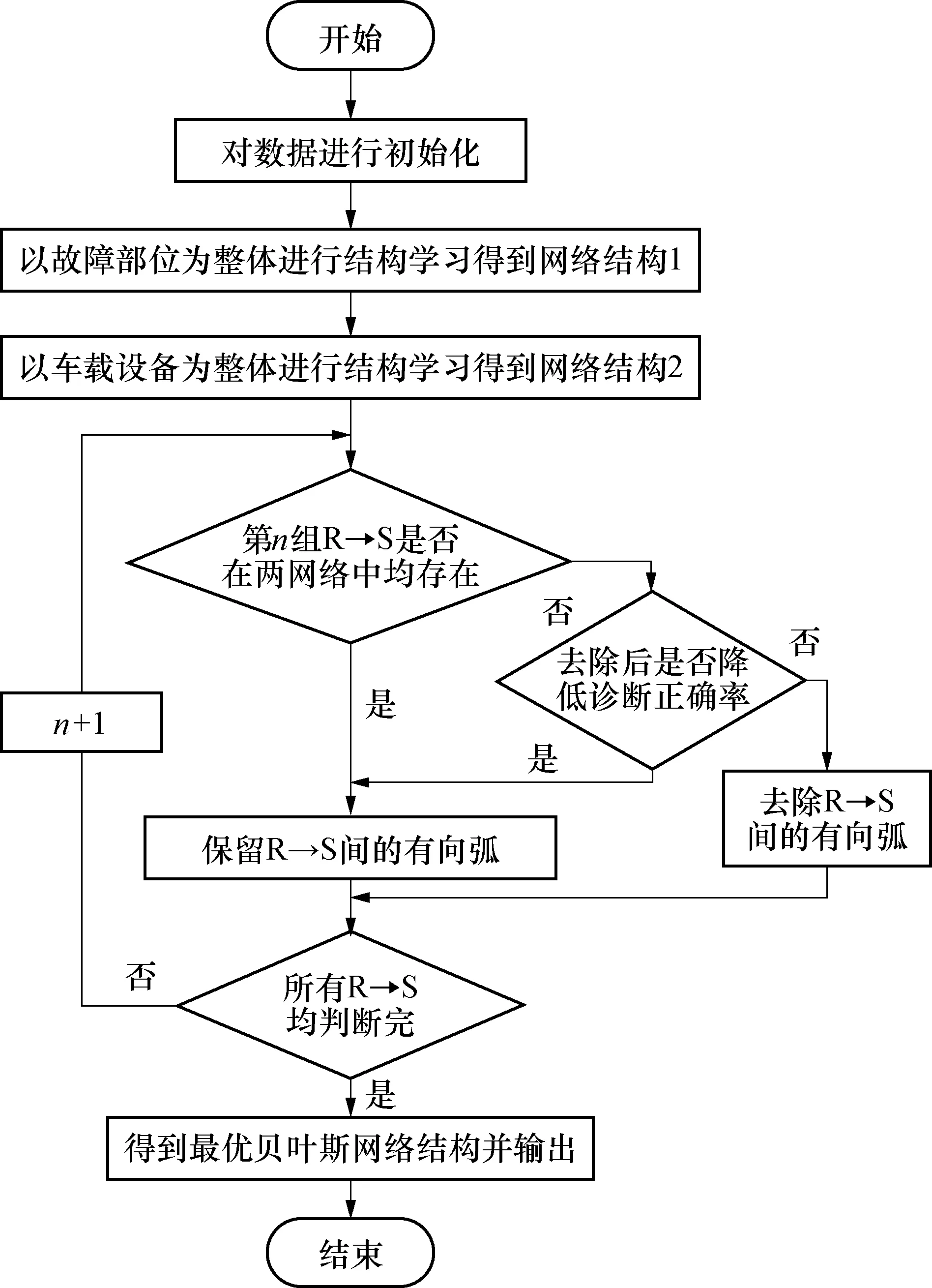
图3 结构学习流程图Fig.3 Flow chart of structural learning
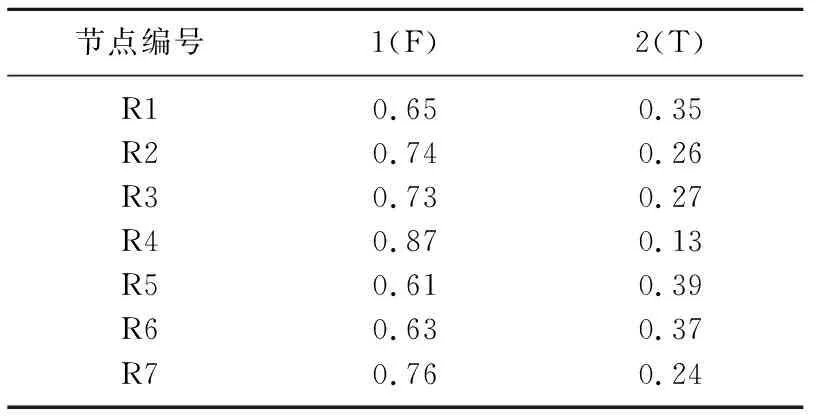
表5 部分故障原因节点的CPT
3 验证分析
根据故障记录数据对列控车载设备贝叶斯网络故障诊断模型进行仿真,分析其故障诊断的精度.
3.1 仿真设计
本文以Matlab为仿真平台,利用Kevin Murphy所编写的BNT工具箱实现对模型的搭建,包括结构学习、参数学习和诊断推理.其中诊断推理的流程如图5所示.
在贝叶斯网络故障诊断模型中,通过改变证据节点变量,从而影响整个网络的概率分布,根据后验概率大小确定故障诊断结果.显然,这是一个由已知结果寻求未知原因的过程,因此选择联合树推理引擎进行诊断推理.
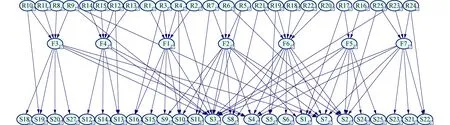
图4 最优贝叶斯网络Fig.4 Optimal Bayesian network

图5 诊断推理流程Fig.5 Flow of diagnostic reasoning
3.2 数据集描述及可信度分析
通过分析可知故障部位是故障诊断的结果,也是定位故障原因的一个支撑,现以故障部位为依据对样本数据的分布进行描述,具体的故障类型及其所占比例如表6所示.
为了验证本文所提出的最优贝叶斯网络故障诊断模型的可靠性,从F1值和kappa系数两个评价指标验证其可信度.计算原理如下
F1=2PR/(P+R)
(6)
式中:P为精确率;R为召回率,经计算得F1值为0.871 1.
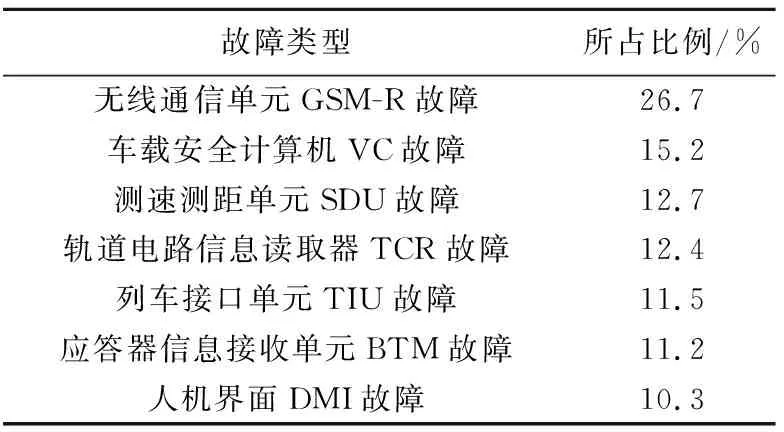
表6 样本数据分布情况Tab.6 Distribution of sample data
kappa系数的计算原理为
(7)
式中:Po为总体分类精度.
(8)
式中:N为样本的类别数;n为样本的总个数;Tni为真实的i类样本数;Pni为预测的i类样本数.
经计算得kappa系数为0.8585.综上所述,结合评价标准可知最优贝叶斯网络模型的诊断结果与实际情况基本一致,具有较高的可信度.
3.3 诊断推理
从故障数据中选取一个案例进行验证,这里以GSM-R(F1)部位发生的车地通信异常(R1)故障而出现无线超时(S9)、制动(S3)、C3转C2(S10)故障征兆为例,1代表不发生,2代表发生,则该故障案例的故障征兆数据输入形式为
S={1,1,2,1,1,1,1,1,2,2,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1}
(9)
输入故障征兆证据节点后,经过概率更新可得到各故障部位的后验概率如表7所示.可以看出F1的后验概率最大,因此可判断发生故障的部位是GSM-R.
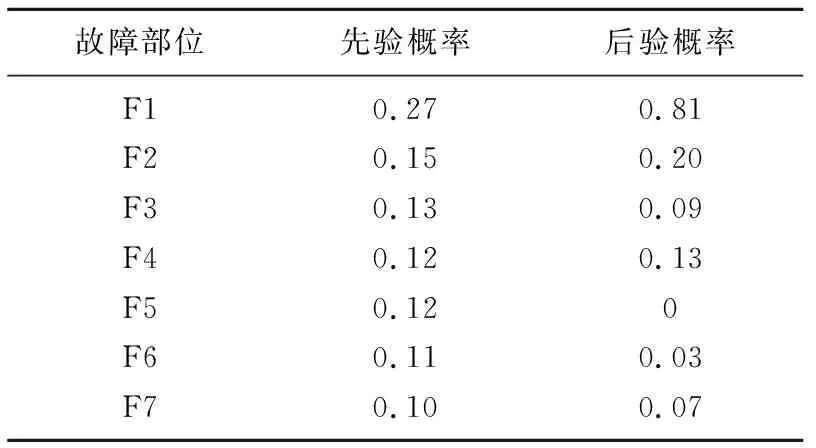
表7 故障部位诊断结果Tab.7 Diagnosis results of fault location
故障原因的推理诊断结果如图6所示,从结果可以看出R1发生故障的概率最大,即由先验概率0.076 3变为0.661 4,可判断故障原因为R1.

图6 故障原因诊断结果Fig.6 Diagnosis results of fault reasons
另外,为了简化贝叶斯网络的节点数,增强学习效果,也以各故障部位为整体进行了模型的搭建与学习,这里选择列车接口单元TIU为例进行推理验证.首先结合专家知识和故障记录数据集搭建列车接口单元故障诊断模型,其次针对列车接口单元故障诊断网络的特点,选择可视化较强的GeNIe软件进行仿真分析.选取列车接口单元发生继电器故障(R16)为测试案例,在输入主机与DMI通信中断(S2)、制动(S3)、停车(S4)的故障征兆证据节点后,可得到如图7所示的诊断结果.
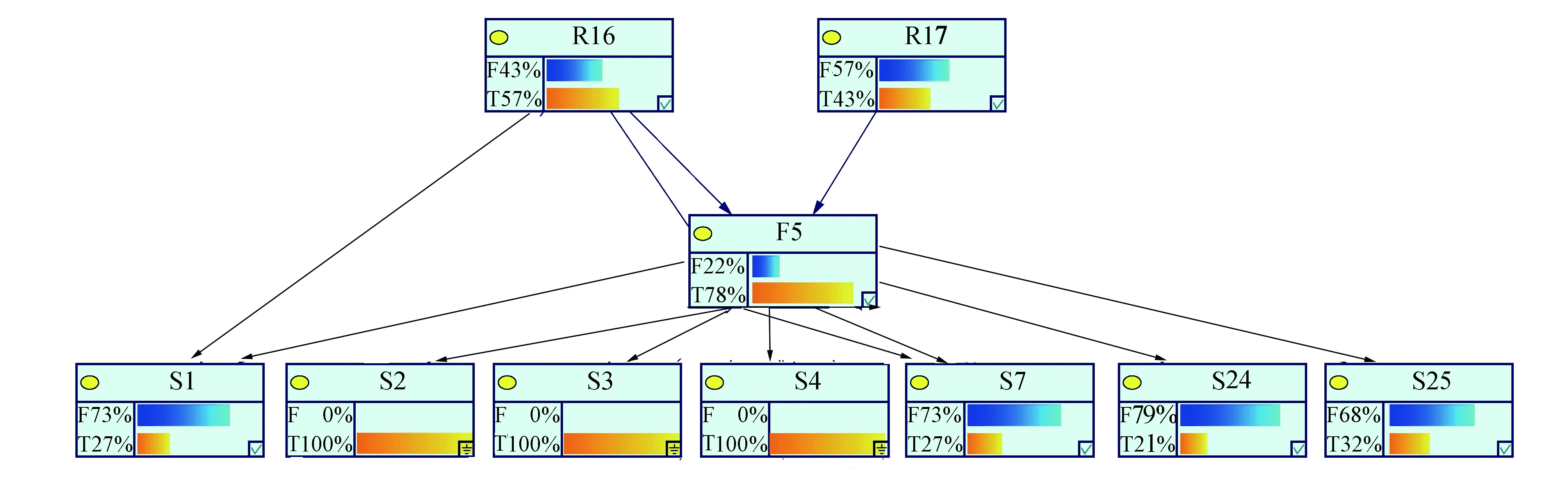
图7 TIU的诊断模型及推理过程Fig.7 Diagnosis model and reasoning process of TIU
从图7中可以看出,在输入故障征兆证据节点进行概率更新后,R16故障的概率为57%,R17故障的概率为43%,因此得出故障原因为继电器故障,诊断结果与测试案例中的实际记录情况一致.
3.4 对比分析
利用Matlab仿真平台的BNT工具箱,对基于专家知识的贝叶斯网络模型(A模型)、以车载设备为整体进行学习的贝叶斯网络模型(B模型)和最优贝叶斯网络模型(C模型)进行诊断推理,得出如图8所示每个诊断模型各车载设备子系统的诊断正确率.
从图8中可得,最优贝叶斯网络模型的诊断正确率得到了一定程度的提升,诊断结果更加准确。经计算,本文所提出的故障诊断模型的平均正确率达到了88.20%,较基于专家知识的贝叶斯网络模型的40.68%提高了一倍,较以车载设备为整体进行学习的贝叶斯网络模型的69.88%提高了18.32%.

图8 诊断结果对比Fig.8 Comparison of diagnostic results
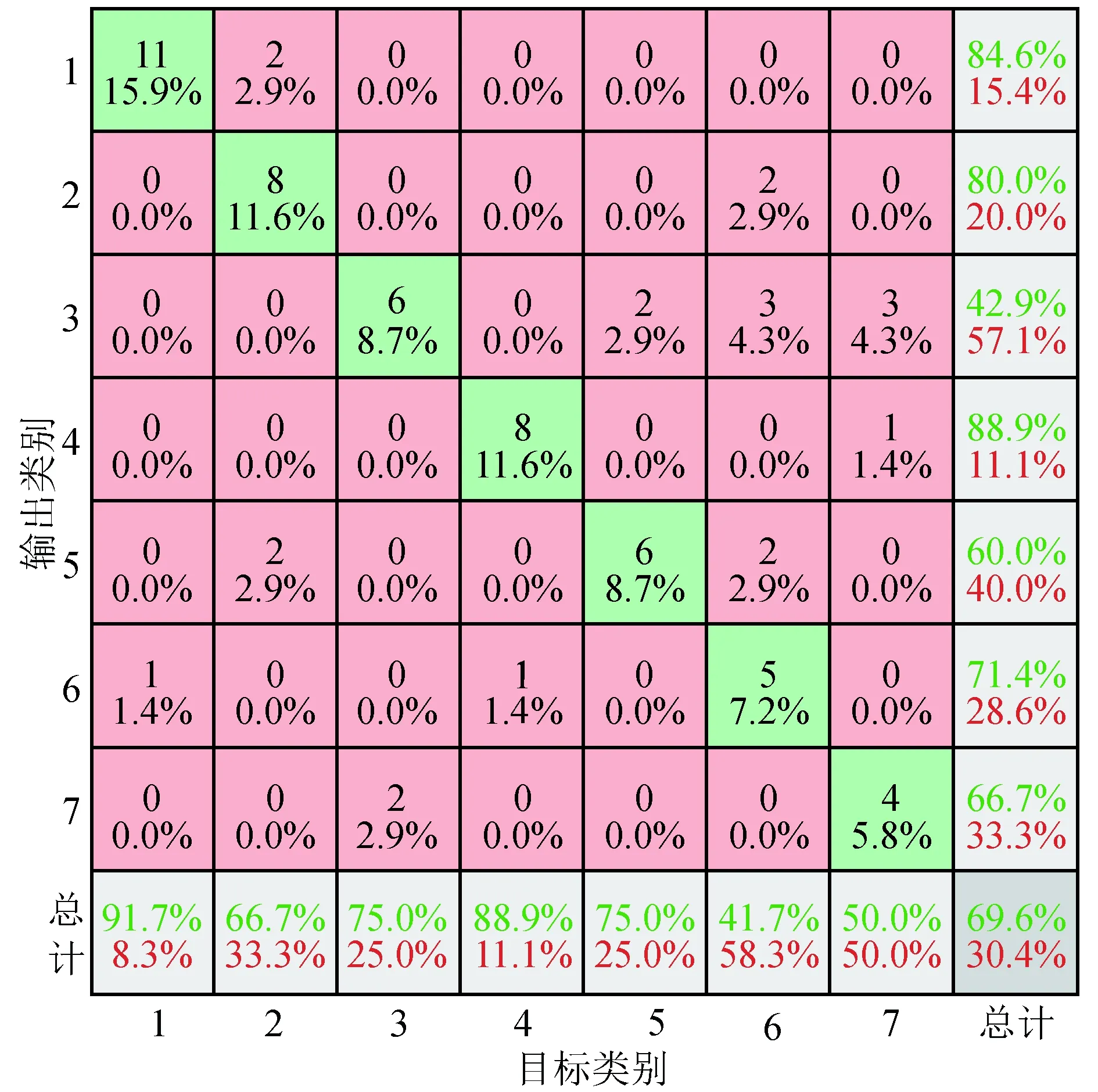
图9 神经网络的诊断结果的混淆矩阵Fig.9 Confuson Matrix of NN diognostic results
除此之外,为了验证本文所提出的贝叶斯网络故障诊断方法相比于神经网络和SVM的优越性,分别使用神经网络和SVM算法在相同的数据下对列控车载设备的故障进行诊断.首先采用神经网络方法,选取样本集的80%作为训练集对神经网络模型进行训练,剩下的作为测试集,用来验证其正确率.通过仿真得到测试集的故障诊断结果见图9.其中,最后一行为对应目标类别数据的分类结果总概率,最后一列为对应输出类别的分类结果总概率.从图9的混淆矩阵中可以看出,基于神经网络的列控车载设备的故障诊断正确率为69.6%,相对较低.接下来以相同的训练数据和测试数据来验证基于SVM的列控车载设备故障诊断性能,结果如图10所示.
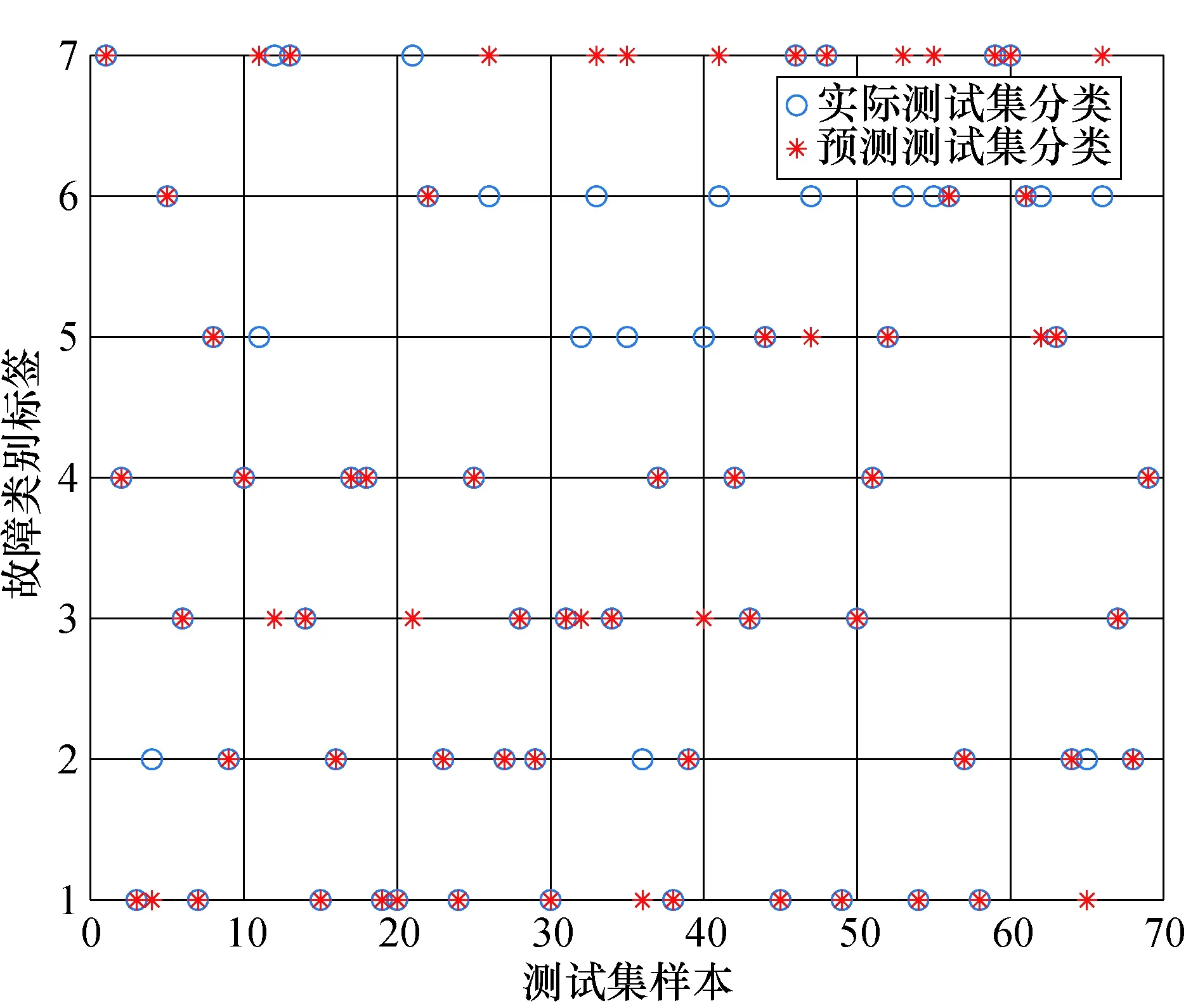
图10 SVM方法的诊断结果Fig.10 Diagnostic results of SVM
经计算使用SVM方法对列控车载设备进行故障诊断的正确率为75.36%,虽稍优于神经网络,但仍不够理想.由此看来,使用贝叶斯网络的方法可以改善高速铁路列控车载设备的故障诊断正确率.
4 结论
1)针对CTCS3-300T型列控车载设备的故障特点,引入贝叶斯网络解决其故障诊断问题,降低了处理该不确定性问题的难度.
2)在专家知识的基础上,将各故障部位的诊断模型与整个列控车载设备的故障诊断模型进行融合,改善了建模过程.分别采用K2算法和极大似然参数估计算法进行结构学习和参数学习,优化了贝叶斯网络故障诊断模型.
3)实验结果表明,与神经网络、SVM相比,本文所提出的方法能够提高列控车载设备故障的诊断正确率,可以为技术人员精准定位故障提供有力支撑,具有一定的参考意义.
