基于改进Steger算法的线结构光中心提取

曾凯，刘贺飞，何茜，王福斌，邸跃

(华北理工大学 电气工程学院，河北 唐山 063210)

引言

线结构光三维视觉测量技术作为一种有效的光学测量方法，具有非接触、准确度高和良好的实时性等优点，在工业生产、逆向工程、计算机视觉等领域得到广泛应用。提取光条图像的条纹中心坐标是线结构光三维视觉测量技术的关键，光条图像包含被测量物体表面的三维形貌信息，是被测点三维坐标求取的依据[1]。光条中心线坐标提取的偏差将直接影响被测对象三维坐标的精度[2]。由于噪声对条纹中心提取存在一定的影响，因此如何充分利用光条图像特征，实现条纹中心的快速、高精度提取，是三维视觉测量技术首要考虑的问题。

李丹等[3]将极值法和灰度重心法相融合，首先利用极值法找到灰度值的最大点，然后通过灰度重心法获取光条的中心位置，此方法充分利用了图像的灰度信息，将2种方法的特点相结合，提高了条纹中心提取的准确性和快速性，但是也存在抗噪能力差的缺点。贺忠海等[4]提出了曲线拟合法，实现了亚像素提取的高精度和高稳定性，鲁棒性良好，但是检测提取速度慢，并且不适合复杂情况下激光条纹的检测。李凤娇等[5]对Steger 算法做出改进，可根据宽度值的差异性确定光条中心点坐标，但当激光条纹中心提取时，中心点和边缘点之间的距离问题使运算效率降低。吴庆阳等[6]对方向模板法进行优化，应用可变的方向模板确定条纹法线的方向，并结合灰度重心法在法线方向提取条纹的中心，使提取精度得到提高，但该方法只采用了固定方向的模板，导致计算误差较大。蔡怀宇等[7]在Steger算法的基础上，用主成分分析法(PCA)代替Steger算法中利用Hessian 矩阵求特征值的过程，该方法避免了对图像进行多次二维高斯卷积，提高了提取速度，保证了提取精度，满足系统实时性的需求。

在实际测量中，一些工件表面存在不同程度的腐蚀或污染现象，并且表面的金属材料反光现象严重，导致激光反射率不均匀使光条图像受到较大的环境影响，易造成光条图像离散性较大[8]。为解决激光条纹图像的质量问题，提出一种自适应卷积模板结合改进Steger算法的结构光条纹中心提取法。该方法通过自适应卷积模板有效减弱噪声，对去噪后的图像进行阈值分割快速得到条纹的感兴趣区域，再采用Steger法根据区域中条纹的线宽分段，精确提取图像中条纹的亚像素位置，提高了系统精度与计算效率，并且适用于高亮面物体的检测。

1基本原理

1.1 结构光条纹特性

线结构光是一种单色线激光。灰度值在光条截面上呈对称高斯分布，灰度值最大点是条纹中心。但由于被测物体本身性质的影响，例如材质是否均匀、透光性能如何、材料本身的颜色、形状和表面光滑度等问题[9]，造成被测工件表面对光的反射率并不均匀，即在相机坐标系中，与理想情况相比，这种偏差将会使被测物体表面反射的条纹截面光强度的分布发生改变，从而致使条纹截面的灰度值呈非正态分布，即一种不对称的近似高斯分布。

图1(a)为非正态分布的条纹图像, 其真实的条纹中心在水平直线上，但灰度值明显偏离真实中心位置并在其两侧波动。图1(b)为正态分布的条纹图像，其灰度值基本对称分布。

图1 不同正态分布的条纹

1.2 基于Hessian矩阵的Steger算法

Steger算法将图像视为二维函数，利用Hessian矩阵计算特征值和特征向量，得到条纹中心法线的方向，并在法线方向上将条纹灰度分布根据泰勒多项式展开，然后获取对应法线上的极值点，即在条纹截面灰度分布曲线上，一阶导数为0，二阶导数为负的极小值点，也就是所求取得条纹截面中心亚像素点。通过求取激光条纹图像像素点 的Hessian 矩阵特征值和对应的特征向量来得到光条中心点法线方向[10]。Hessian矩阵表示为：

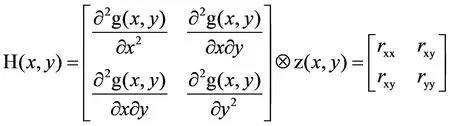
(1)

式中：g(x,y)是二维高斯函数。

设nx,ny是经Hessian矩阵求出的条纹法线方向的单位向量，以点(x0,y0)为标准点，对条纹截面灰度分布函数进行二阶泰勒展开，则条纹横截面上点(x0+tnx,y0+tny)的灰度为：

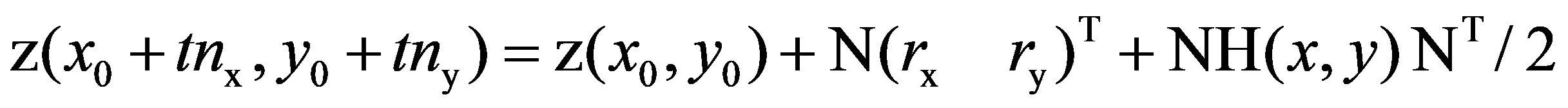
(2)

其中N=(tnx,tny)，rx、ry由z(x,y)和与之相应的微分形式的高斯核卷积得到。如下式：

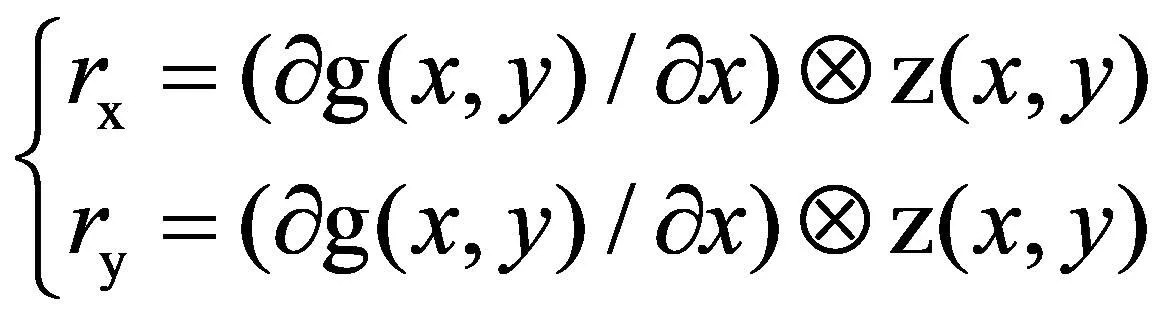
(3)

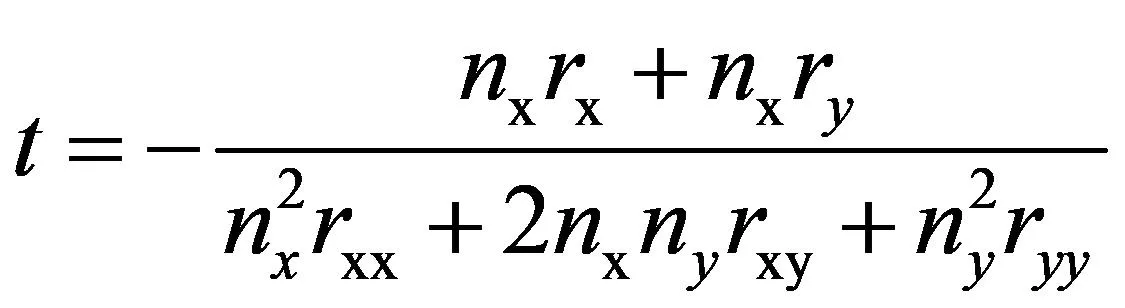
(4)

可得出条纹中心点精确位置为(x0+tnx,y0+tny)。

由于Hessian矩阵运算量大，其中每个点都要进行5次(rx、ry、rxy、rxx、ryy)二维高斯卷积，导致计算效率低造成系统实时性下降，因此，需要在保证精度的基础上，对Steger算法进行改进，适当提高Steger算法的计算效率。可以利用高斯卷积的可分离性和对称性，将二维高斯核等效分解为一次高斯行卷积和一次高斯列卷积，将运算量从5n2次乘加运算减少到6n+4次乘加，即从根本上减小对于大模板卷积的计算量[11,12]。

2改进Steger算法用于线结构光中心提取

2.1 自适应卷积法

通常情况下，通过图像预处理不能理想地消除噪声干扰。当激光投射到粗糙的物体表面时，采集图像并进行阈值分割和中值滤波预处理，得到图2所示图像，图中噪声没有被完全消除，导致条纹中心提取的精度下降，为提高提取精度，采用一种基于激光条纹中几何信息和相关性的自适应卷积法来减弱噪声。

图2 粗糙表面条纹预处理

首先计算自适应模板的大小，自适应模板的大小和元素值取决于激光条纹中的几何信息和相关性，通过滑动模板达到去除噪声的目的[13]。自适应模板的获取可以简述为：

Step1:在图像预处理之后，计算行(或列)中非零灰度像素的数量。

Step2:通过收缩矩阵来移除零元素，得到一个新的矩阵K，其中Km表示矩阵中最大值，Kp表示矩阵中所有元素的平均值。

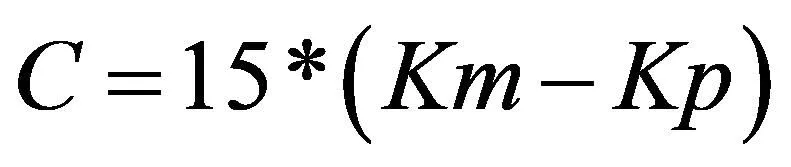
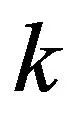
从图3(a)可以明显观察到对原图像使用自适应模板进行卷积后噪声减弱，激光条纹的轮廓得到了完好地保留。然后使用大津法对图像进行阈值分割[14]，选定阈值并对图像进行二值化处理，从背景中提取出图3(b)所示的感兴趣区域。因此，通过上述一系列图像处理，获得了最佳的条纹区域，有效消除了噪声对条纹中心提取的干扰，并且显著提高了光条提取速度，实现了测量系统的实时要求，使之后的处理步骤更加简化。

图3 自适应卷积和阈值分割处理后的图像

2.2 几何中心法提取条纹粗略中心点

在实际测量环境下，由于被测物体本身表面通常伴有粗糙、高反光等干扰因素，往往造成得到的光条图像的条纹宽度不一致，因此，条纹中心线直接提取很难达到其精度要求。在得到了条纹的感兴趣区域后，运用几何中心法粗略提取条纹中心点，该研究使用Canny算法进行边缘检测[16]，边缘检测完成后计算其几何中心，计算所得结果作为条纹粗略中心点，按照列查询的方式，分别检测每行中的最上和最下的非零像素点对应的行坐标值，取其平均值作为中心坐标。图4分别为经过处理后边缘图像和边缘及边缘中心线图像。

图4 边缘图像和边缘及中心线图像

2.3 条纹中心亚像素提取

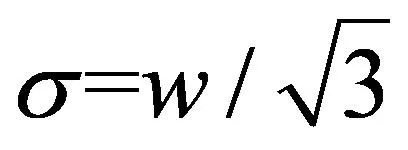
(5)

其中，M，N为光条行号。

3实验分析

利用实验室中的线结构光三维测量系统，验证算法的准确性和有效性，线结构光测量系统主要由0-30MW线结构光激光器、分辨率为1 600×1 200的德国Allied Vision TechnologieMako G-192C摄像机组成，采用Matlab软件编程实现。测量对象为2种表面光滑的矩形工件，拍摄到的光条图像如图5所示，图5(a)表明工件表面光滑、反射率相对均匀，有轻微的反光现象，光条图像质量较好；图5(b)表明测量工件表面反射率不均匀，光条图像较离散，反光严重，图像质量不高。

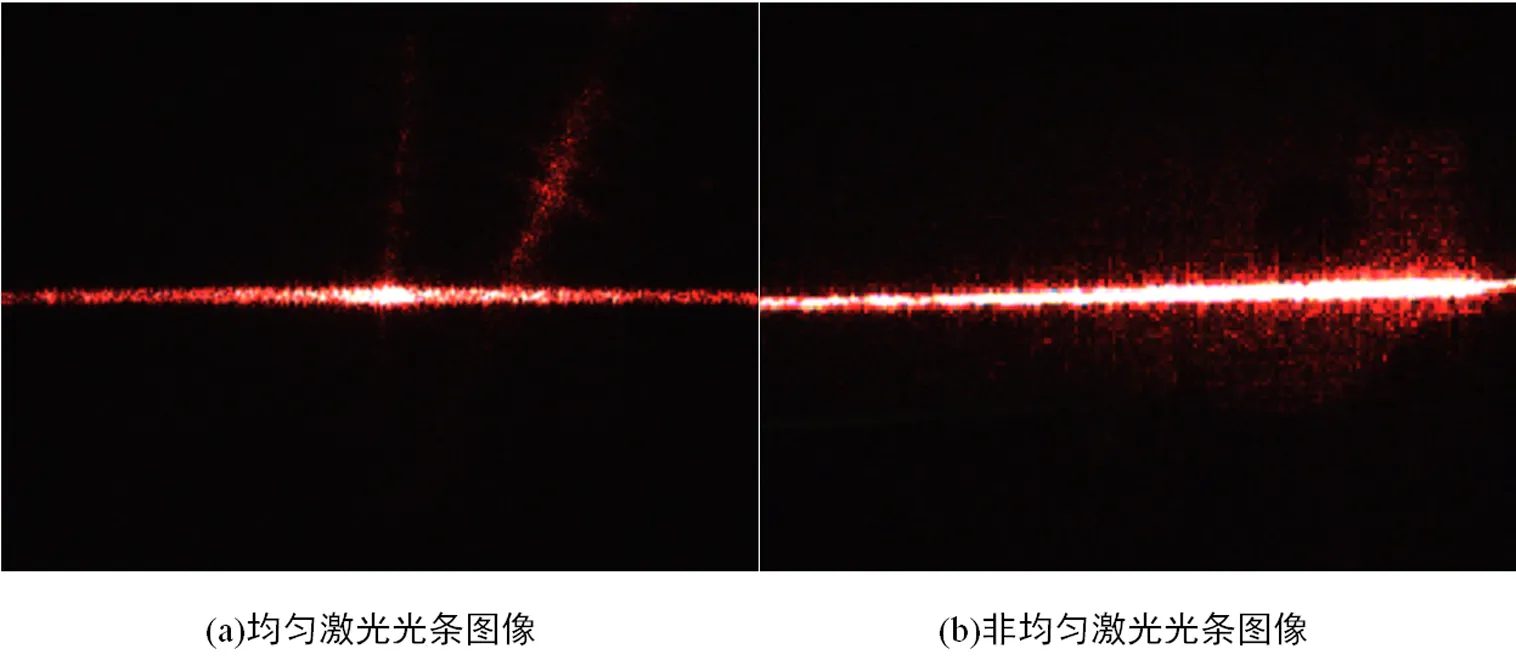
图5 工件光条图像

采用相同滤波参数及线宽对两幅激光条纹图像进行预处理，第1列为灰度重心法，可以看出提取的中心线波动较大；第2列为基于Hessian 矩阵的Steger 方法，与灰度重心法对比，中心线较为平整；第3列为本文算法，其适应性更好，提取效果最佳。

图6 3种算法提取的光条中心线图像

测量对象为工件表面，对提取结果分别进行直线拟合，并计算所有数据点到拟合直线的均方差。通过对比均方差的大小来判断算法的测量精度，均方差越大则测量精度越低，表明该算法提取光条中心的准确性较低；均方差较小，则该算法提取光条中心的准确性较高[19]。表1为使用3种不同算法提取2种光条图像中心线，并计算获得的数据点与拟合直线的均方差数据。

表1 3种光条中心线提取方法均方差

通过表1中的数据可以得出，对于亮度均匀且质量较好的光条，3种算法求得的数据点到拟合直线距离的均方差较小，光条的中心线提取较为准确；对于光条较离散且质量较差的情况，灰度重心法的均方差已偏离很大，对比其他2种方法，该研究算法的均方差相对较小，可以准确地提取光条中心线，进而为后续的三维测量打下良好的基础。

4结论

通过对线结构光的中心提取实验，提出了一种自适应卷积结合改进Steger算法的条纹中心线提取方法。利用自适应卷积模板有效地降低了噪声对图像的干扰，之后利用几何中心法提取条纹粗略中心点，根据光条区域的宽度不同，设定不同的高斯函数均方差σ，利用Hessian 矩阵及泰勒级数实现激光条纹宽度变化的中心线检测，提高了Hessian矩阵的获取速度，满足测量的实时性要求，精度可达到亚像素级。该方法稳定性强、精度高，适合对高反光物体的光条中心提取，有利于提升结构光的三维重建的效率。