Anomalous anisotropic magnetoresistance in single-crystalline Co/SrTiO3(001)heterostructures∗
2021-12-22ShuangLongYang杨双龙DeZhengYang杨德政YuMiao缪宇CunXuGao高存绪andDeShengXue薛德胜
Shuang-Long Yang(杨双龙), De-Zheng Yang(杨德政), Yu Miao(缪宇),Cun-Xu Gao(高存绪), and De-Sheng Xue(薛德胜)
Key Laboratory for Magnetism and Magnetic Materials of the Ministry of Education,Lanzhou University,Lanzhou 730000,China
Keywords: single crystalline,anisotropic magnetoresistance,heterostructure
1. Introduction
The anisotropic magnetoresistance (AMR) effect, discovered in ferromagnetic metals by Thomson in 1857,[1]is one of the most fundamental characteristics involving magnetic and transport properties[2]and has many practical applications in magnetic recording and sensors.[3]This phenomenon is attributed to spin–orbit coupling which mixes spin-up state with spin-down state,[4–6]and is usually studied in magnetic materials (MMs). While the combined MM with some nonmagnetic materials can form bilayers or multilayers, and thus lots of novel magnetoresistance (MR) phenomena are discovered,such as giant MR in Fe/Cr/Fe,[7]tunneling MR in Fe/MgO/Fe,[8]spin Hall MR(SMR)[9]in ferromagnetic insulator[10,11]or metal,[12]unidirectional SMR[13]in Co/Pt and Co/Ta, Hanle MR in Pt/YIG,[14]anisotropic interface MR in Pt/Co/Pt,[15–17]Rashba–Edelstein MR in Bi/Ag/CoFeB,[18]and spin–orbit MR in Cu[Pt]/Y3Fe5O12.[19]Although the above MR phenomena originate from different physical essences, they are dependent on spin–orbit coupling and heavily correlated with the nonmagnetic materials or interface.
Interestingly,nonmagnetic oxide SrTiO3(STO)substrate also has a strong influence on transport properties of a thin film deposited on it. In LaAlO3/STO heterostructures, interfacial Rashba MR,[20]fourfold oscillation AMR and planar Hall effect,[21]as well as giant crystalline AMR[22]were reported.[23–25]Besides these outstanding studies devoted to single crystalline oxides, a few fantastic phenomena in metals/STO heterostructures were realized. In nonmagnetic metallic Al/STO heterostructures, two-dimensional electron gas was formed at room temperature[26]and a very large inverse Edelstein effect[27]was reported. In half-metallic Fe4N/STO heterostructures, the AMR becomes positive,[28]which is opposed to its natural negative AMR on Si substrate.[29]In addition, more and more studies on AMR have been conducted based on single-crystal magnetic thin films recently,for it can exhibit strong dependence on the current orientation,[30–38]additional four-fold symmetry,[31,34–38]and asymmetric behaviors.[33]However, the signs of above AMR are always positive,and the negative AMR(a fingerprint for half-metallicity[39,40]has never been realized in metallic films. It is interesting to explore whether the single-crystal MM/STO heterostructures show different AMR properties.
In this paper,we study the AMR in the single-crystalline face-centered-cubic (FCC) Co(6 nm)/STO(001) heterostructure as a function of temperature and current direction. The AMR with the current along Co[100] (Co[110]) direction shows anomalous negative (positive) longitudinal MR and positive (negative) transverse MR below 100 K. The anomalous temperature-dependence of the AMR can be well understood by a phenomenological model and attributed to the interplay between the non-crystalline component from the traditional AMR and the crossed AMR component from a mixture of current and crystalline direction related contributions.
2. Experimental details
Co/STO(001)heterostructures were prepared by molecular beam epitaxy in an ultrahigh vacuum chamber with a base pressure better than 4.5×10−10Torr (1 Torr = 1.33322×102Pa). The (001)-oriented Co layers were deposited on STO(001) by using thermal evaporator with a substrate temperature held at 400◦C. The Co crystallinity was monitored byin situreflection high-energy electron diffraction(RHEED)during deposition,and further improved byin situannealed at 400◦C for 15 min after deposition. Finally, the heterostructures were covered by a 3-nm-thick Al capping layer to prevent the Co film from oxidizing.High resolution x-ray diffraction (HRXRD) was used to characterize the structure. Magnetic properties were measured with Verslab (Quantum Design). Using standard lithography and Ar-ion etching,the heterostructures were patterned into two Hall bars along Co[100]and Co[110] crystalline directions. The transport properties were performed by using a standard four-probe method with a constant DC currentIin a physical property measurement system(quantum design)equipped with a rotatable sample stage.To exclude contributions from the possible misalignment, we did the measurements with both positive and negative field directions.
3. Results and discussion
Figure 1(a) shows the RHEED patterns of Co films and STO substrate with the electron beam along the STO[100]and STO[110] directions, respectively. The elongated stripes of both Co[100]and Co[110]patterns show the formation of an FCC (001) surface. Theθ–2θx-ray diffraction of the 6-nmthick Co film shown in Fig.1(b)is consistent with that of the FCC structure. The in-plane lattice parameter calculated from the Co(002) peak is about 3.542 ˚A. The lattice mismatch between Co and STO[100] (3.905 ˚A) is 9.3%, which is almost the same as previous result.[41]
Figure 1(c)shows the hysteresis loops measured at room temperature with an in-plane external magnetic field along the Co[100] and Co[110] directions, respectively. The [110] direction as the easy axis(EA)can be clearly seen from the FCC Co film. For the hard-axis loop (H ‖Co[100]), by applying separate linear fits to the saturated high field and the region between 20 mT and 0 mT, we extract the in-plane magnetocrystalline anisotropy[42,43]of 42.4 mT between the[100]axis and[110]axis. The temperature-dependent zero-field resistivities are depicted in Fig. 1(d) for these two crystalline directions. The resistivities in the two directions decreases clearly with temperature decreasing, as usual. However, the resistivity ofI ‖Co[100] is larger (smaller) than that ofI ‖Co[110]when the temperature is above(below)150 K.The crystalline direction-dependent resistivity indicates that the MR can be different in the Co[100] direction from in the Co[110] direction.

Fig.1. Characterization results of Co/STO(001)films. (a)RHEED patterns with incident electrons along STO[100]and STO[110]directions. (b)X-ray diffractions (θ–2θ scan). (c) Magnetic hysteresis loop measured at 300 K with magnetic field applied along Co[100] and Co[110] directions. (d) Resistivity ρxx measured for I‖Co[100]and I‖Co[110]. The inset shows the sketch of measurement geometry. The unit a.u. is short for arb. units.
The longitudinal resistivityρxxmeasured as a function of magnetic field applied to the film plane forI ‖Co[100]andI ‖Co[110] are shown in Fig. 2, where the field parallel and perpendicular to the current. Each of Figs. 2(a) and 2(b)indicates that the field-dependentρxxis almost linear andρxx(H‖I)>ρxx(H⊥I) for two current directions when the magnetization is saturated at 300 K. However, the results at 5 K shown in Figs. 2(c) and 2(d) display a nonlinear field dependence[42]ofρxx,ρxx(H‖I)<ρxx(H⊥I)forI‖Co[100]andρxx(H‖I)>ρxx(H⊥I) forI ‖Co[110]. Generally, the resistivity of the current parallel to the magnetization case is larger (smaller) than that of the current perpendicular to the magnetization case,which is defined as the positive(negative)AMR.[2]Hence, the AMRs of two directions are positive, as usual at 300 K, but that at 5 K are negative forI ‖Co[100]and positive forI ‖Co[110]. Moreover, the positive or negative AMR is magnetic field-independent after the magnetization has been saturated. In order to clarify the characteristics of AMR,which are heavily dependent on the current direction and temperature,we study the angulardependent AMR further.

Fig.2. In-plane MR(MR)curves measured at 300 K and 5 K with H‖I and H⊥I,with current direction being along[(a),(c)]Co[100]direction and[(b),(d)]Co[110]direction.
Figures 3(a)–3(d)show the AMR curves of Co[100]and Co[110] Hall bars at various temperatures, where ∆ρxx=ρxx −ρav, ∆ρxy=ρxy,ρavis the averagedρxxover 360◦in plane, andϕis the angle between the external magnetic field and current directions. The field is of constant magnitude 6 T,which is sufficient to saturate the magnetization in plane.Hence,the magnetization is expected to be parallel to the field.The longitudinal AMR curves with current along Co[100]and Co[110]are shown in Figs.3(a)and 3(b). It is found that the angles where the maximum values located are shifted gradually fromϕ=0◦and 180◦at 300 K to nearlyϕ=90◦and 270◦at 5 K for the Co[100]Hall bar. However,the AMR observed in Co[110]Hall bar always shows a maximum atϕ=0◦and 180◦.The sign of AMR changes from positive at 300 K to negative at 5 K for Co[100]Hall bar but it is always positive for the Co[110]Hall bar. These results are different from those of the polycrystalline Co,[2,45,46]as well as the single crystalline FCC Co/LaAlO3(001),[30]where the AMR is positive along different directions. Moreover, the current-direction related AMRs reported in FCC Ni/MgO(001),[31]Fe/GaAs,[32,33]and CoxFe1−x/MgO[34]show an unchanged sign except the symmetry of AMR changing with temperature decreasing. These results demonstrate that the current direction and temperature significantly influence the longitudinal AMR of Co/STO(001)heterostructure.
Furthermore, the transverse AMR is measured and the results are shown in Figs. 3(c) and 3(d). As is well known,the physical origin of traditional longitudinal and transverse AMR[2]are the same,hence,the transverse AMR should have the same corresponding trace as the longitudinal AMR.However, the sign of transverse AMR is changed from positive at 300 K to negative at 5 K for the Co[110] Hall bar, but the transverse AMR is always positive for the Co[100] Hall bar.These results of the transverse AMR never appear in Co,[47,48]Fe/GaAs,[33]or CoxFe1−x/MgO,[34]which only show the positive behaviors.The different temperature-dependent behaviors of the longitudinal and transverse AMR for two Hall bars enlighten us to consider the contribution of crystal symmetries.
Phenomenologically, a model presented by Rushforthet al.[35]according to symmetry,[49]by extending the model of D¨oring[50]to systems with cubic plus uniaxial anisotropy can be used. As described in this model,[36–38]the longitudinal and transverse AMR both as a function of the angleϕbetween magnetizationMand the in-plane currentI,and the angleψbetweenMand the[110]crystalline direction is written as
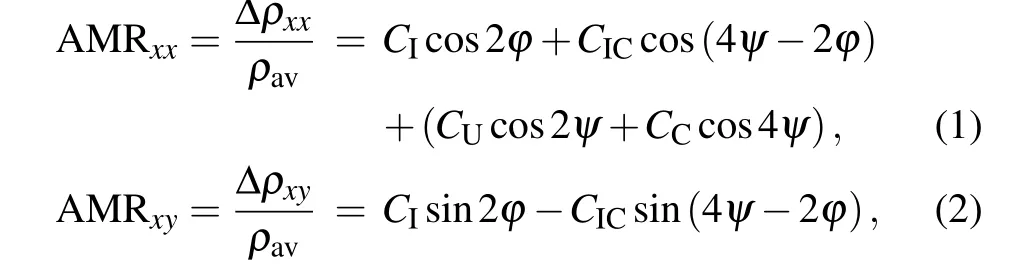
where the coefficientsCIandCICrepresent the non-crystalline term and the crossed term,CUandCCdenote the lowest order uniaxial crystalline term and cubic crystalline term, respectively. ForI ‖Co[100],ϕ=ψ −45◦, and forI ‖Co[110],ϕ=ψ. As shown in Fig.3,the experimental data can be well fitted by the corresponding equations.
Combing Eqs. (1) and (2), the coefficientsCI,CIC,CU,andCCobtained by fitting the longitudinal and transverse AMR ofI ‖Co[110] orI ‖Co[100] are shown in Fig. 4(a).It can be seen that bothCIandCICare larger thanCU, andCU>CC≈0. As shown in Eqs. (1) and (2) (CI−CIC)terms determine the twofold-symmetry of both the longitudinal AMR inI ‖Co[100](ψ=45◦) and transverse AMR inI ‖Co[110](ψ=0◦).CI
In addition,the strong temperature-dependent AMR amplitudes for the two current directions can be quantitatively elucidated. We plot ∆AMRxx= AMRxx(ϕ=0◦)−AMRxx(ϕ= 90◦) and ∆AMRxy= AMRxy(ϕ=45◦)−AMRxy(ϕ=135◦)versustemperature in Fig.4(b). ∆AMRxx(∆AMRxy) is small (large) forI ‖Co[100], and ∆AMRxx(∆AMRxy) is large (small) forI ‖Co[110]. In addition,∆AMRxxinI ‖Co[100] is almost equal to ∆AMRxyinI ‖Co[110], andvice versa. The unambiguously reciprocal relations of AMR amplitudes between the two current directions are coincident with the phenomenological expansions based on symmetry from Eqs. (1) and (2). Furthermore, the ratio∆AMR[100]xy/∆AMR[110]xyhas a drastic change with temperature and reaches a maximum 29 at 100 K as shown in Fig. 4(c),which is much larger than the other results 1–5.[30–33]Meanwhile, ∆AMR[110]xx/∆AMR[100]xxhas the same dependence on temperature. The large anisotropic dependence on temperature for AMR[37]means that larger AMRxxor AMRxycan be chosen for designing magnetic sensor or magnetic memory devices with the fixed current direction.

Fig. 3. Curves of in-plane longitudinal and transverse AMR versus ϕ for current along [(a), (c)] Co[100] direction and [(b), (d)] Co[110]direction,with solid linedenoting the experimental data by using Eqs.(1)and(2).

Fig.4. (a)Curves of fitting coefficients CI,CU,CC, and CIC versus temperatures. (b)∆AMRxx and ∆AMRxy for I‖Co[100]and I‖Co[110]with decreasing temperature. (c)Amplitude ratio ∆AMR[110]xx /∆AMR[100]xx (red)and ∆AMR[100]xy /∆AMR[110]xy (blue)versus temperatures.
Furthermore, the AMR under a non-saturated magnetic field is measured, where the magnetization direction is determined by the competition between the applied field and the magnetic anisotropy.[51–54]With 100-mT field, longitudinal AMR ofI ‖Co[110] and transverse AMR ofI ‖Co[100]are obtained in Fig. A1 (Appendix A: Supplementary materials). The fitted cubic (uniaxial) anisotropy fieldHK(HU),and the angleθK(θU) between the current direction and the easy axis (EA) of cubic (uniaxial) anisotropy field at 300 K are listed in Table 1. The value ofHKis close to 42.4 mT obtained from hysteresis loop in Fig. 1(c). A smallerHUis along the Co[110]direction,which can be attributed to the inplane strain induced by the unavoidable miscut on the STO substrate. A similar anisotropy fieldHKobtained from magnetic and AMR measurement demonstrates that the AMR may be related to the symmetry of magnetic anisotropy rather than crystalline symmetry.

Table 1. Fitted HK,HU,θK,θU from Fig.A1 at 300 K.
Theoretically, the non-crystalline termCIdepends only on the relative angle between current and magnetization direction. The influence of another dominant term, crossed termCIC,on AMR is studied by varying the thickness of Co. Here,Co(2 nm)/STO and Co(2 nm)/STO heterostructure are measured in a way similar to previous way, and the results are shown in Fig.A2(Appendix A:Supplementary materials). It is found that the crossed termCICis larger(smaller)than noncrystallineCIfor Co(2 nm in thickness)(Co(20 nm in thickness))film. Experimentally, the values of relatively largeCIChave been observed for(Ga,Mn)(As,Sb)films,[37]for which the possible reason is the large strain or bulk spin–orbit coupling due to the incorporation of Sb. Further studies indicate thatCICdepends on the magnitude (rather than direction) of interfacial spin–orbit field(SOF)[22]as well,while the interfacial SOF induced by the reduced structural symmetry at surfaces and interfaces will be relatively weaken[32]at large thickness. Hence, the anomalous AMR of the Co(6 nm in thickness)/STO heterostructure is closely related to the interface.
4. Conclusion
In this work,the anomalous AMR behaviors in the singlecrystalline FCC Co/STO(001)heterostructures are observed.Both the magnitude and the sign of the longitudinal ARM and transverse AMR are dependent on the temperature and the current direction. It is shown that these effects are attributed mainly to the interplay between the non-crystalline component and crossed component. The nature of the anomalous AMR is closely related to the symmetry of magnetic anisotropy and the interface SOF.Our research highlights the significant properties of the Co/STO (001) heterostructures,but more investigations are still required to further clarify the microscopic mechanism behind the magneto-transport behavior in MM/STO system.
Appendix A:Supplementary materials
A1 Magnetic anisotropies determined by magnetoresistance measurements
For the single domain approximation of a singlecrystalline film, using the coherent rotation model, the free energy density of the system can be written as[52,53]

whereµ0is the vacuum permeability,Msis the saturation magnetization,ϕH(ϕM)is the field(magnetization)angle the current direction,Ku(Kc) is the uniaxial (cubic) anisotropy constant,θKu(θKc) is the angle between uniaxial (cubic)anisotropy and the current direction.α=ϕH −ϕMcan be obtained by(∂E)/(∂α)=0 with small angle approximation

whereh1=H/Hk,h2=Hu/Hk,HkandHuare the effective cubic and uniaxial anisotropy fields. TheφMcan be determined by the angledependent magnetoresistance measurement. Hence, combining Eq. (A2) with Eq. (1) or Eq. (2) in the main text,Hk,Hu,θk,θucan be quantified by fitting the magnetoresistance curve.

Fig. A1. (a) Longitudinal magnetoresistance for I ‖Co[110] and fitted by combining Eq. (A2) with Eq. (1). (b) Transverse magnetoresistance for I‖Co[100]and fitted by combining Eq.(A2)with Eq.(2).
Figures A1(a) and A1(b) show longitudinal magnetoresistance forI‖Co[110]and transverse magnetoresistance forI‖Co[100]withH=100 mT at 300 K.The fitted results are shown in Table 1 of the main text.
A2 Magnetoresistance in Co(2 nm)/STO(001) and Co(20 nm)/STO(001)
Co(2 nm)/STO(001) and Co(20 nm)/STO(001) films are prepared and measured in a way similarto previous way and the coefficients fitted with the above phenomenological model are shown in Fig.A2.The non-crystalline term and the crossed term are the dominant terms similar to the Co(6 nm)/STO,but non-crystalline term is clearly smaller(larger)than the crossed term over the whole temperature range in Co(2 nm)/STO(001)(Co(20 nm)/STO(001)).

Fig.A2. Curves of fitted AMR coefficients CI,CU,CC,and CIC versus temperature of(a)Co(2 nm)and(b)Co(20 nm),respectively.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Transient transition behaviors of fractional-order simplest chaotic circuit with bi-stable locally-active memristor and its ARM-based implementation
- Modeling and dynamics of double Hindmarsh–Rose neuron with memristor-based magnetic coupling and time delay∗
- Cascade discrete memristive maps for enhancing chaos∗
- A review on the design of ternary logic circuits∗
- Extended phase diagram of La1−xCaxMnO3 by interfacial engineering∗
- A double quantum dot defined by top gates in a single crystalline InSb nanosheet∗
