Nonlinear dynamical stability of gap solitons in Bose–Einstein condensate loaded in a deformed honeycomb optical lattice∗

Hongjuan Meng(蒙红娟) Yushan Zhou(周玉珊) Xueping Ren(任雪平)Xiaohuan Wan(万晓欢) Juan Zhang(张娟) Jing Wang(王静)Xiaobei Fan(樊小贝) Wenyuan Wang(王文元) and Yuren Shi(石玉仁)

1College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China

2Key Laboratory of Atomic and Molecular Physics&Functional Materials of Gansu Province,Northwest Normal University,Lanzhou 730070,China

Keywords: gap soliton,Bose–Einstein condensate,deformed honeycomb optical lattice

1. Introduction

Bose–Einstein condensate (BEC) in optical lattices has generated considerable interesting research for studying many quantum phenomena in periodic potentials.[1–4]It arises in many applications ranging such as quantum simulators[5–7]and quantum computation.[8]The cubic lattice is a simple representative example of an optical lattice. Experiments with ultracold atoms have utilized exotic lattices such as triangular,[9]honeycomb,[10]and Kagome lattices.[11]The honeycomb optical lattices can lead to significantly different results due to the underlying symmetries. A special feature of a perfect honeycomb lattice is the two-lowest-band-formed Dirac points.These unique characteristics could provide new opportunities to investigate many interesting physical phenomena in many systems such as monolayer graphene,[12,13]electron gases in semiconductors,[14]coupled photonic lattices,[15,16]and photonic waveguides.[17]

On the other hand,the interplay between lattice periodicity and atomic interaction brings a large number of interesting nonlinear effects.[18–20]In many cases, periodicity relates to the band structure of the dispersion relation and Bloch waves.Meanwhile,the nonlinearity can induce self-phase modulation and can also couple waves between different modes or Bloch bands. The existence of the nonlinearly localized structures that reside in the linear energy gaps has attracted considerable interest in recent years.[21–23]They are sometimes referred to as gap solitons,which are often considered theoretically as bifurcations from the Bloch-band edges into the band gaps.[24,25]The general properties of gap solitons have been intensively studied in many different nonlinear periodic systems, examples include but are not limited to optical waveguide arrays and photonic lattices,[26,27]semiconductor microcavities,[28]and BEC in optical lattices.[1,23,29,30]

Gap solitons in honeycomb optical lattice have been studied both theoretically and experimentally.[17]The authors of Ref. [31] demonstrated the gap solitons residing in the gap between the second and the third bands in honeycomb photonic lattices. In Ref. [32], the authors showed solitons and necklaces in the first band gap of a two-dimensional optically induced honeycomb defocusing photonic lattice. In Ref.[33],the authors studied gap solitons in honeycomb dynamical lattices with the cubic nonlinearity. However,there is still great significance to study gap solitons of BEC in honeycomb optical lattice,especially for the interplay between the honeycomb optical lattice and the nonlinearity affects on the existence and dynamical stability of multipole gap solitons.

Here, we investigate gap solitons of BEC in deformed honeycomb optical lattices with atomic interaction and study their nonlinear dynamical stability. Deformed honeycomb lattices are promising platforms. With the deformation of the honeycomb lattice,the symmetries can be broken,then a gap opens between the first two bands,and the lattice can support a gap soliton.[34,35]The existence of the gap soliton provides a way to detect the symmetry breaking. The deformed honeycomb lattices have been studied extensively,such as nonlinear wave packets,[36]Klein tunneling,[37]fractional topological quantum states,[38]nondegenerate chiral phonons,[39]and topological valley transport.[40]

In this paper, we show the linear band-gap structure of the deformed honeycomb optical lattices and the existence of the gap solitons. We find that the system admits dipole gap solitons both in the first gap and in the semi-infinite gap, depending on the repulsive or attractive properties of atomic interactions. The dipole gap soliton can have their bright solitary structures be in-phase or out-of-phase. Then,we analysis the nonlinear dynamical stability of these dipole gap solitons by using direct simulations of the Gross–Pitaevskii(GP)equation.Finally,we derive the envelope equations of Bloch waves and analyze these gap solitons.

The paper is organized as follows: In Section 2,we introduce the model of BEC in deformed honeycomb optical lattices. In Section 3,we show the linear band-gap structure and the existence of the gap solitons. Following this,the analysis of nonlinear dynamical stability of the gap solitons is given in Section 4.Finally,we give summary and conclusion in Section 5.

2. Model of BEC in a honeycomb optical lattice

We consider that BEC is loaded in a honeycomb optical lattice. The honeycomb optical lattice can be experimentally generated by superposing three coplanar traveling laser beams.[41,42]The three coplanar traveling laser beams have the same angular frequencyωL=ck0withk0being the wave vector of the radiation. Then, the lattice potential is denoted byV(r)with[35]

Fig. 1. Contour plot of the potential energy for (a) η =1 (the optical lattice has a perfect standard graphene-like honeycomb),and for(b)η=0.6(the optical lattice becomes a deformed honeycomb).The white dotted line in the figure is a schematic diagram of the corresponding lattice sites.

3. Gap solitons and theoretical analysis

3.1. Band-gap structure

In this subsection, we show the band-gap structure and the existence of the gap solitons. We first investigate the linear band-gap structure of the deformed honeycomb optical lattices. Let us consider quantum mechanical of BEC in such periodic potentials. Gap solitons are stationary solutions to Eq. (2), we can apply Bloch’s theorem, which suggests that the Bloch waves are the nonlinear eigenstates of the following formΨ(r,t)=φk(r)exp(i(k·r −µt)).[44]Hereµis a real chemical potential, andφkhas the same period as the potential.Then we can obtain the following equation for each Bloch wave stateφk:The set of eigenvaluesµ(k)then forms Bloch bands.

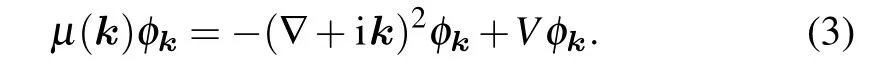
Since gap solitons only exist in the linear energy gaps between the Bloch bands,it is important to first identify the positions of these gaps. To do this,we can neglect the nonlinear terms, i.e.,g=0, and calculate the linear Bloch spectrum by numerical diagonalization of Eq.(3). The band gap spectrum generated by the solution of the linearized version of the equations is shown in Fig. 2. Due to the expected periodicity of the solution to Eq. (3), there are several numerical methods to find the Bloch waveφk.[45–47]We use Fourier collocation method[48]for numerically computing these Bloch bands.

In Fig.2,we only show the lowest five Bloch bands. One can see that a band gap[49]is separated by the two Bloch bands.The lowest gap below the lowest Bloch band is called the semiinfinite gap and the higher gaps are called the first band gap,the second band gap,and so on.

Fig.2. (a)The linear Bloch band gap structure of BEC in a deformed honeycomb optical lattice as a function of k(left). (b)Axial side view of the linear Bloch band gap structure as a function of kx,shaded areas correspond to the linear bands.

The band gap structure of BEC in honeycomb optical lattices depends not only on the depth of the optical lattices but also on the degree of deformed honeycomb. Figure 2 shows how the band gap structure of BEC in honeycomb optical lattices is affected by lattice depthV0and deformation parameterη.

Figure 3(a) shows the energies of different Bloch bands overlaping for a suffciiently small lattice depthV0,in this case no other band gap appears except the semi-infniite gap. With increasing lattice depthV0, the window of band gap will become more and more obvious.Figure 3(b)shows that the band gap structure depends on the deformation of the honeycomb.Forηchanging in the range<η ≤1,the smaller theη,the more deformed the honeycomb lattice. With increasingη,the frist gap becomes narrower and narrower and eventually disappears. Figure 3(b) shows an interesting phenomenon, that is,the more deformed the honeycomb lattice,the more prominent the frist gap. For a standard honeycomb lattice, the frist gap does not exist.Therefore,in order to obtain gap solitons in the frist gap,one must choose a deformed non-standard honeycomb lattice.In this article,we choose a deformed honeycomb lattice forη=0.6 as an example.

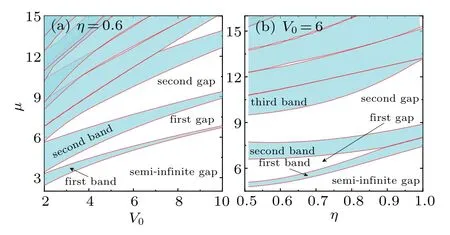
Fig. 3. The band gap structure of BEC in honeycomb optical lattices with increasing lattice depth(a)and deformation parameter η (b).

3.2. The gap solitons

The interplay between spatial periodicity and nonlinear dynamical evolution harbors a large number of interesting physical many-body effects. Gap solitons is the existence of unique soliton solutions that reside in the linear energy gaps between the Bloch bands. Gap solitons spatially localized in gap modes may appear as a result of the balance between the dispersion and the nonlinearity. For BECs in an optical lattice,the hoppings between different lattice sites play the role of dispersion,and the atom-atom interaction brings the nonlinearity.

In what follows, we consider the nonlinearity brought from the atom-atom interaction and stationary solutions in the linear Bloch bands gaps. We look for gap solitons by numerical methods such as the Newton conjugate-gradient (NCG)method,[50]which is based on iterating certain time evolution equations associated with the linear stability eigenvalue problem and is one of the powerful numerical techniques to find the solitary wave solutions of a nonlinear evolution equation.The methods are applied to compute both the ground states and excited states in a large number of physical systems with and without periodic potentials. We take the Gaussian profile as the initial condition for iterating. One can adjust the amplitude,width and center position of the initial Gaussian profiles to get the wanted gap solitons. For example, in order to obtain unipole gap solitons, the initial Gaussian wave packet is mainly distributed in a certain potential well.In order to obtain the dipole gap solitons,the initial two Gaussian wave packets are mainly distributed in two adjacent potential wells.

After numerical techniques mentioned above,we find the unipole gap solitons in the semi-infinite gap. Figure 4(a)shows gap solitons in the semi-infinite gap withµ=4.8 andg=−1 as an example. Figure 4(b)shows gap solitons in the semi-infinite gap withµ=5.01 andg=−1 as an example.The gap solitons in the first gap can be obtained withg>0.

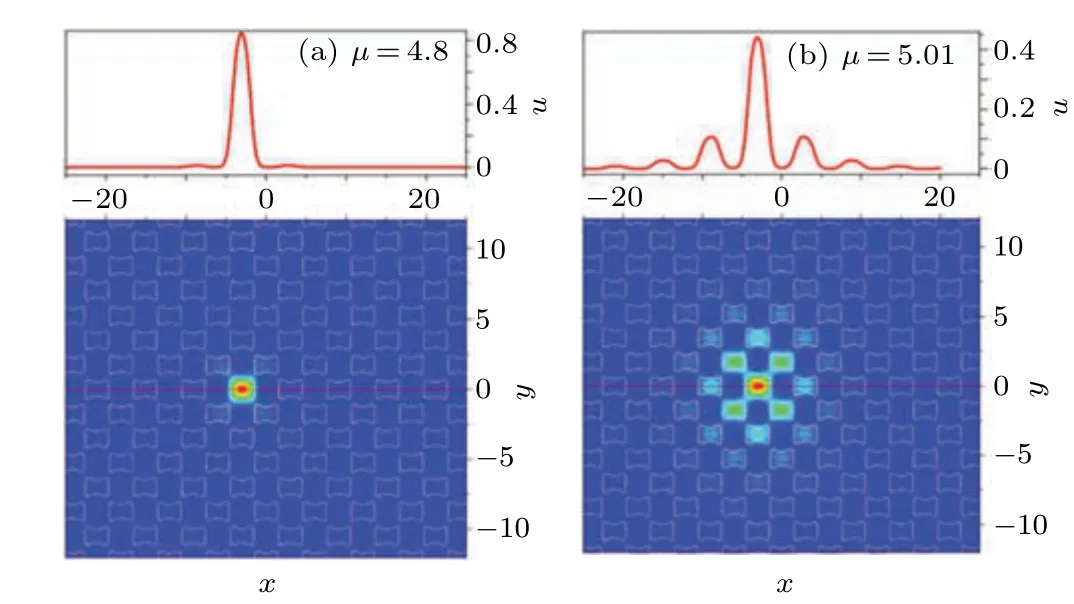
Fig.4.Gap solitons in the semi-infinite gap with attractive atomic interaction g=−1.0:(a)forµ=4.8,(b)forµ=5.01.The white dotted line in the figure is a schematic diagram of the corresponding lattice sites.

In order to study the properties of gap solitons more clearly,we pay attention to effect of nonlinear eigenenergyµon the amplitude of the gap solitons and the total power of gap solitons. In order to see this, we define the amplitudeAand the total powerPof the gap solitons given as follows:

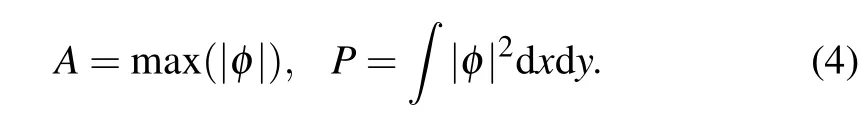
In Fig. 5, we show amplitudeAand powerPof the gap solitons for nonlinear eigenenergyµwith respect to on-site interactiongin the range of the band gap. Here, we modulate the nonlinear eigenenergyµfrom semi-infinite band gap to first band gap. Here,we takeg=−1 andg=1 as examples for gap solitons in semi-infinite band gap and first band gap,respectively. When the nonlinear eigenenergyµmoves toward the band,numerical results indicate that the amplitude of gap solitons both in semi-infinite gap and in first gap approach to infinitesimal. However, when the nonlinear eigenenergyµmoves toward the band,the power of gap solitons both in semiinfinite gap and in first gap approach to infinity.

There is a very interesting phenomenon shown in Fig. 5 for the powerPof the gap solitons versus eigenenergyµin the range of the band gap. When the nonlinear eigenenergyµmoves toward the band, the powerPof gap solitons both in semi-infinite gap and in first gap decreases slowly first, then increases gradually. This means that the relationship between the amplitudeAand powerPof the gap solitons is inconsistent with the eigenenergyµ,they move in step whenµfarther away from the band,and they move out of step whenµcloser to the band. Thus, they are bifurcated from the Bloch band edges.

Fig.5.The amplitude A and power P of the gap solitons versus eigenenergy µ in the range of the band gap. Shaded areas correspond to the linear bands.

It is worth emphasizing that the appearance of gap solitons both in the first gap and in the semi-infinite gap depends on the repulsive or attractive properties of atomic interactions.The first gap solitons appear only in repulsive atomic interactions regime (g> 0). On the other hand, semi-infinite gap solitons appear only in attractive atomic interaction regime(g<0). The gap solitons are intrinsically related to the extended Bloch waves,[51–54]which can be understood from this perspective of the composition relation between Bloch waves and gap solitons.[52,55]With this composition relation, many conclusions can be drawn for gap solitons from Bloch waves in nonlinear periodic systems. The reason why the appearance of gap solitons in different gaps depends on the properties of atomic interactions is that the atomic interactions of different properties have different effects on the Bloch waves.[52,55]

Next,we show dipole gap solitons in the semi-infinite gap withµ= 4.8 andg=−1 in Fig. 6 as an example, (a) for the out-of-phase gap solitons, (b) for the in-phase gap solitons. The dipole gap solitons in the first gap which are similar to solitons of the semi-infinite gap can also be obtained withg>0. In order to study the properties of dipole gap solitons more clearly,we pay attention to effect of nonlinear eigenenergyµon the total power of dipole gap solitons in Fig.7. The amplitudes of the dipole gap solitons in the first gap and in the semi-infinite gap are similar to unipole gap solitons. In Fig.7(a),when the nonlinear eigenenergyµmoves toward the band, the powerPof gap solitons of in-phase in the semiinfinite gap and out-of-phase in the first gap decreases slowly first, then increases gradually. We call gap solitons such that they are bifurcated from the Bloch band edges. In Fig. 7(b),when the nonlinear eigenenergyµmoves toward the band,the powerPof gap solitons of out-of-phase in the semi-infinite gap and in-phase in the first gap decreases slowly. We call gap solitons such that they are not bifurcated from the Bloch band edges.

Fig. 6. Dipole gap solitons in the semi-infinite gap with attractive atomic interaction g=−1.0 andµ =4.8(a)for out-of-phase gap solitons and(b)for in-phase gap solitons.

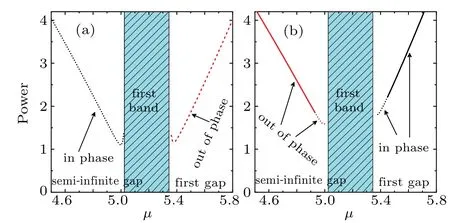
Fig.7. The power P of the dipole gap solitons versus eigenenergyµ in the range of the band gap. Shaded areas correspond to the linear bands.

3.3. Theoretical analysis of gap solitons

In this subsection, we derive the envelope equations of small-amplitude Bloch-wave packets from edges of Bloch bands. Considering the stationary solutionsψ(r) of Eq. (2)with the formΨ(r,t)=ψ(r)e−iµt. When the solutionψ(r)is infinitesimal,this solution is a linear superposition of these two Bloch modes. Whenψ(r) is small but not infinitesimal,this solution then becomes a combination of these two Blochwave packets and can be expanded into a multiscale perturbation series:

Atε3,the equation forψ2is

The solution to Eq.(7)has the following form:

Equation (10) is the leading-order two-Bloch-wave packets,whereX=εxandY=εyare slow spatial variables of envelope functionsA1andA2.

The solution to Eq.(8)is

Substituting theψ0,ψ1into Eq. (9) and using the Fredholm condition (which requires being orthogonal to the homogeneous solutionsp1(x)p2(y)andp1(y)p2(x)),we can obtain

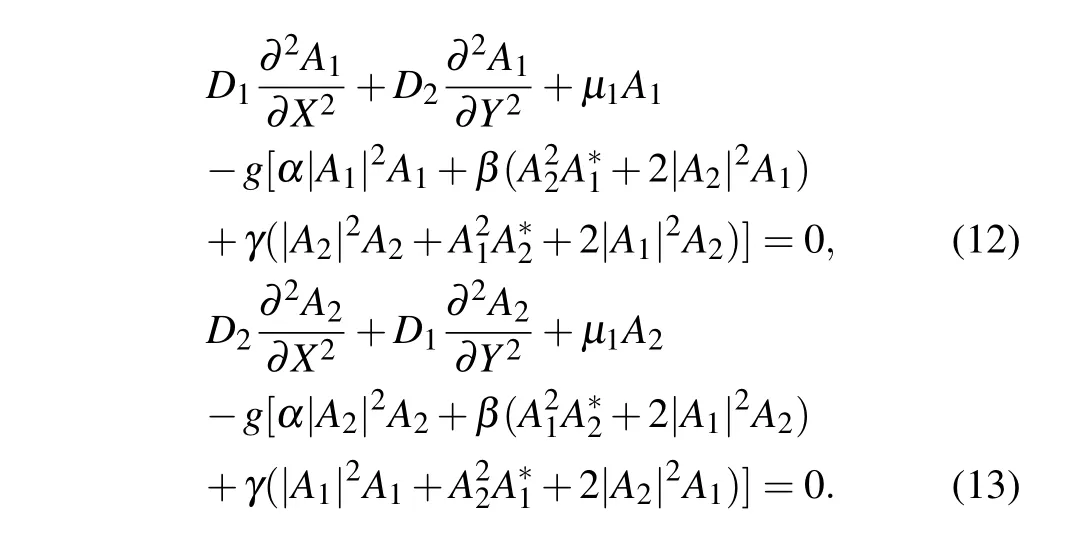
Here,the superscript∗represents complex conjugation,Assume that the modulation wave is a Gaussian profile one,then it can be expressed as

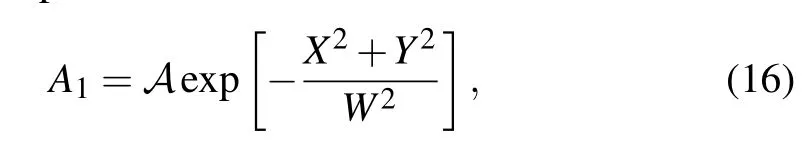
whereAandW(W>0) are the amplitude and width of the solitons, respectively. Note that Eq. (16) is not an exact solution to Eq. (15). Substituting Eq. (16) into Eq. (15) yields the residual error. We minimize the magnitude of the residual error and then have the equation. We solve the equation in a semi-numerical manner,which can be performed easily in Mathematica software by the NSolve command. The results read

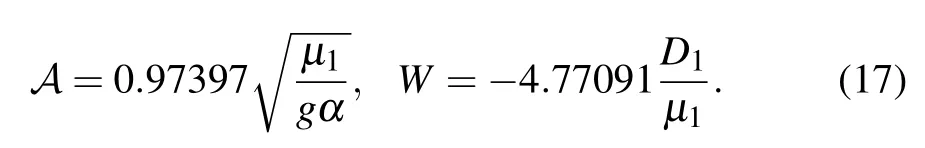
It can be seen from Eq.(17)that the amplitudeAof the soliton depends on the parametersµ1,g,andα,whereas the widthWof the soliton depends on the parametersD1andµ1. Equation(17)also gives the condition for the existence of gap solitons,that is,µ1andgmust have the same sign,butµ1andD1have the opposite signs.In the semi-infinite gap,ifD1>0,one will haveµ1<0 andg<0,with the increase of|µ1|,the value ofµdecreases, and the value ofµis farther away from the band. The amplitude of the soliton increases,which is consistent with the previous numerical results shown in Fig.5. For the first gap,ifD1<0,one will haveµ1>0 andg>0. With the increase of|µ1|,the value ofµincreases,and the value ofµis also farther away from the first band. The amplitude of the soliton increases, which is also consistent with the previous numerical results shown in Fig.5.

4. Linear stabilities and nonlinear dynamical stabilities of gap solitons

Until now, we have shown the existence of unipole and dipole gap solitons of BEC in a deformed honeycomb optical lattice. One unique feature of BEC in optical lattices is the occurrence of instability. To do this,one can analyze the nonlinear and the linear stability of these gap solitons using direct simulations of the GP Eq.(2)and its linearized equation.

4.1. Linear stabilities of gap solitons

The linear stability (so-called Bogolyubov-de Gennes or BdG) analysis is employed in order to consider the fate of small amplitude perturbations and the potential robustness of the solutions. The linear stability of these gap solitons can be modified state and inserted into the time-dependent GP equation. By keeping only the linear term in the perturbation, one can describe the time evolution of the small perturbation,[46,56–58]which yields the linear eigenvalue problem.If the corresponding eigenvalues are real,the perturbation will grow exponentially,which leads to dynamic instability.

Now we study the linear stability of these gap solitons by numerical methods. We perturb these solitons as

The above linear eigenvalue problem (19) can be solved numerically by the finite difference method or the Fourier collocation method.[48]To illustrate,we consider unipole solitons in the semi-infinite gap and in the first gap,as shown in Fig.8.Also,we consider dipole gap solitons in the semi-infinite gap as an example,as shown in Fig.9.Stability spectra for unipole solitons are shown in Fig. 8. It is seen that unipole gap solitons far away from the band have stable eigenvalues and thus are linearly stable in Figs. 8(a) and 8(d). However, unipole gap solitons near the band have unstable eigenvalue and thus are linearly unstable in Figs. 8(b) and 8(c). Figure 9 shows dipole gap solitons of stability spectra in the semi-infinite gap.It is seen that in-phase dipole gap solitons are all linearly unstable in Figs.9(a)and 9(b). Figures 9(c)and 9(d)show that out-of-phase dipole gap solitons far away from the band are linearly stable,and near the band are linearly unstable.

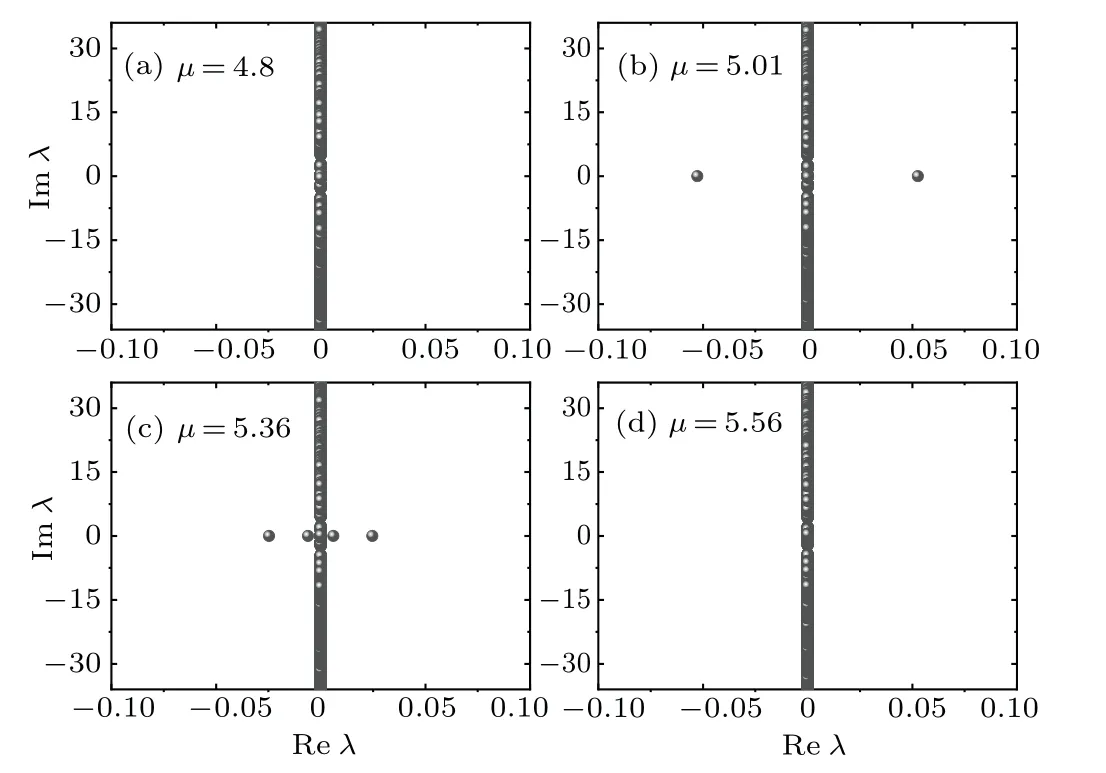
Fig.8. The linear stability analysis of unipole solitons: (a)and(b)for unipole solitons in the semi-infinite gap;(c)and(d)for unipole solitons in the first gap.

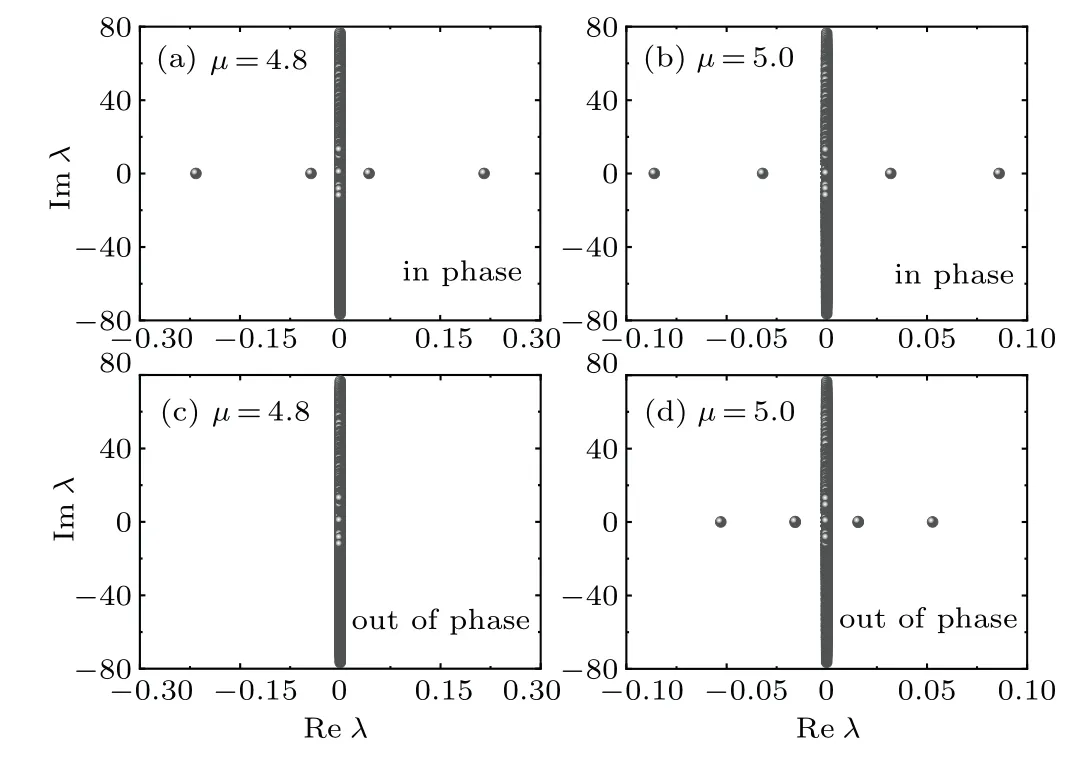
Fig. 9. The linear stability analysis of the dipole gap solitons in the semi-infinite gap:(a)and(b)for in-phase solitons bifurcated from band edges; (c) and (d) for out-of-phase solitons not bifurcated from band edges.

4.2. Nonlinear dynamical stabilities of unipole gap solitons

In the above section, we have analyzed the linear stability problem for unipole and dipole gap solitons. However,the important issue is the nonlinear dynamical stability of these unipole gap solitons and dipole gap solitons,which can be induced by the presence of nonlinear interactions and periodic potential. Dynamical instability implies that small deviations from the stationary solution grow exponentially in time. In order to examine the nonlinear dynamical stability of these unipole gap solitons and dipole gap solitons found above,we directly compute Eq. (2) over a long time. The initial conditions are taken to be the gap soliton with 1%perturbation in the amplitude and phase. We consider a stable gap soliton satisfying the two conditions as follows: it should preserve its peak amplitude,and it should preserve its position on the lattices.

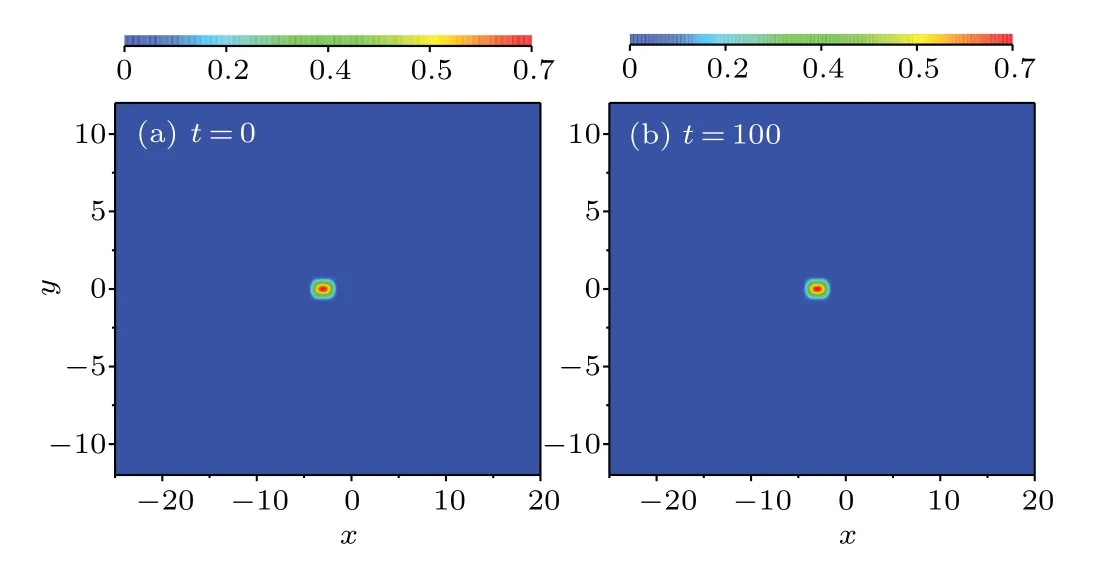
Fig.10. Nonlinear evolution of unipole gap solitons in the semi-infinite gap with µ =4.8 (corresponding to the point a in Fig. 5). The initial conditions were taken with 1%perturbation in the amplitude and phase to trigger potential instabilities: (a)t=0,(b)t=100.

We first consider the nonlinear dynamical stabilities of the unipole gap solitons, and takeµ=4.8 in semi-finite gap as an example (corresponding to the pointain Fig. 5). In Fig.10,we show time evolution of unipole gap solitons in the semi-infinite gap fort=0 and 100. It can be seen from this figure that the amplitude and position on the lattices of the unipole gap solitons are preserved. The gap soliton is nonlinear dynamical stable. This is confirmed by the linear stability analysis in Fig.8(a).

Then, the nonlinear dynamical stability properties of the unipole gap solitons withµ=5.01 is examined, as shown in Figs.11(a)and 11(b)fort=0 and 100,respectively. We cam see the maximum amplitude and the location of the center of mass versus the evolution timet. During the nonlinear dynamical evolution, the peak amplitude undergoes finite-time collapse, its position on the lattice drift-unstable solitons is typically characterized by“humps”that drift from lattice maxima toward nearby minima. Obviously, the unipole gap soliton shows nonlinearly dynamical unstable,which is also confirmed by the linear stability analysis in Fig.8(b).

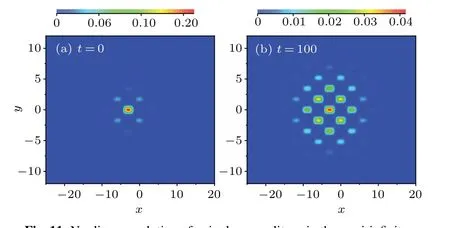
Fig.11. Nonlinear evolution of unipole gap solitons in the semi-infinite gap with µ =5.01(corresponding to the point b in Fig.5). The initial conditions are taken with 1% perturbation in the amplitude and phase to trigger potential instabilities: (a)t=0 and(b)t=100.

In order to examine the nonlinear dynamical stability of unipole gap solitons in the first gap,we also directly compute Eq. (2) over a long time. The initial conditions were taken to be a unipole gap soliton with 1%perturbation in amplitude and phase in Fig.12. It can be seen that the unipole gap soliton shows nonlinearly dynamical unstable and (b) nonlinear dynamical stable. These are also confirmed by the linear stability analysis in Figs.8(c)and 8(d),respectively.

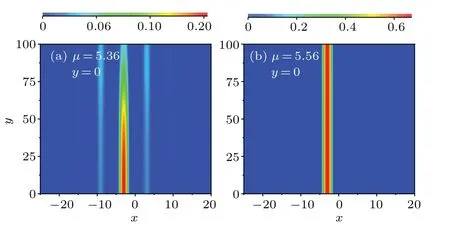
Fig. 12. Nonlinear evolution of the unipole gap solitons in the first gap with repulsive atomic interactions g=1. The initial conditions are taken with 1%perturbation in the amplitude and phase to trigger potential instabilities:(a)µ=5.36 and(b)µ=5.56.The unipole gap soliton corresponds to the points c and d in Fig.5,respectively.

It is well known that the power versusµ, i.e., dP/dµ,plays an important role in determining the stability properties of the solitons. This connection between the slope of the power curve and the linear stability is the so-called Vakhitov–Kolokolov stability criterion.[59]This criterion states that with the continuous change ofµ, a pair of real eigenvalues move towards the origin, collide there,and then bifurcate along the imaginary axis. The power minimum point turns out to be precisely the bifurcation point,which indeed suggests that linear stability of these solitary waves is intimately related to the sign of the slope of the power curve.[48]In a large number of simulations,we have ever plotted the total power versusµfor unipole gap solitons corresponding to the semi-infinite gap and the first gap,and have observed two recurring features:

(a)In the semi-infinite gap,the unipole gap soliton is nonlinear dynamical stable only if its power decreases with increasingµ, i.e., dP/dµ<0(as the nonlinear dynamical evolution of the pointain Fig.5).On the contrary,the unipole gap soliton will be nonlinear dynamical unstable only if its power increases with increasingµ,i.e.,dP/dµ>0(as the nonlinear dynamical evolution of the pointbin Fig.5).

(b) In the first gap, the unipole gap soliton will be nonlinearly dynamically stable only if its power increases with increasingµ,i.e.,dP/dµ>0(as the nonlinear dynamical evolution of the pointdin Fig.5). Meanwhile,the unipole gap soliton will be unstable only if its power decreases with increasingµ,i.e.,dP/dµ>0(as the nonlinear dynamical evolution of the pointcin Fig.5).

The nonlinear dynamical stabilities of unipole gap solitons depend on dP/dµ,which are opposite in semi-infinite gap and first gap. The reason for this phenomenon is that there are different requirements for the properties of atomic interaction when solitons occur in two gaps.

4.3. Nonlinear dynamical stabilities of dipole gap solitons

In the semi-infinite gap, the out-of-phase and in-phase dipole gap solitons exist (shown in Fig. 6) for the attractive atomic interactions regime. Now,we investigate the nonlinear stability properties of the lattice soliton. The in-phase dipole gap soliton corresponds to Fig.6(b). The dynamics of nonlinear evolution of the in-phase dipole gap soliton withµ=4.8 is shown in Fig. 13. Figures 13(a) and 13(b) depict the density profiles of the in-phase dipole gap soliton fort=0 and 100, respectively. In fact, in the semi-infinite gap, for all inphase dipole gap solitons their nonlinear dynamic evolution will show a similar phenomenon nonlinearly dynamical unstable,as seen in Fig.7(a).In the first gap,the in-phase dipole gap solitons satisfy the condition dP/dµ>0. Solutions near the band have unstable eigenvalues and thus are linearly unstable.However, solitons far away from the band have no unstable eigenvalues and thus are linearly stable.

Fig. 13. Nonlinear evolution of the in-phase dipole gap soliton in the semi-infinite gap with repulsive atomic interactions g=−1. The inphase dipole gap soliton corresponds to Fig.6(b). The initial conditions are taken with 1% perturbation in the amplitude and phase to trigger potential instabilities.

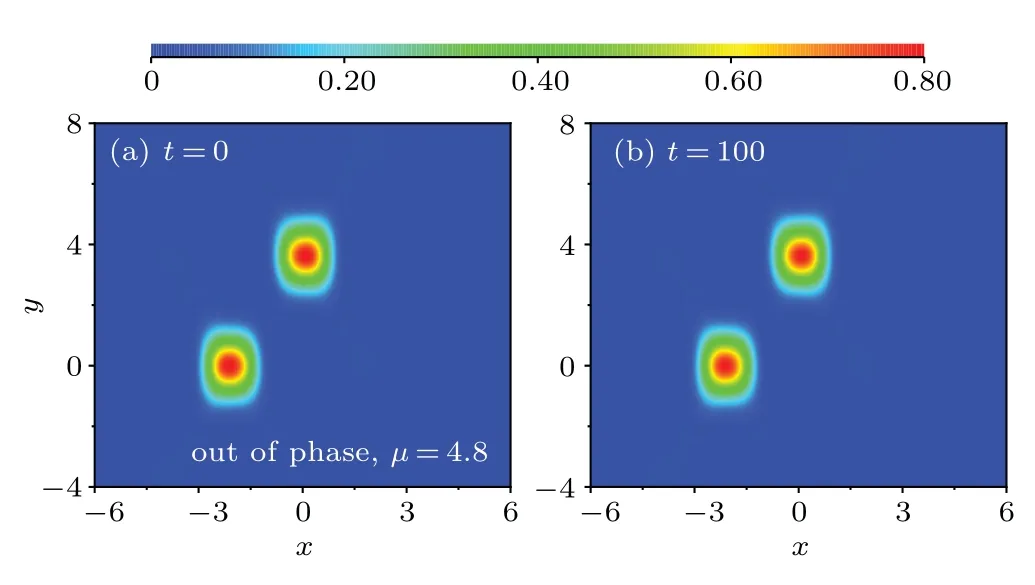
Fig. 14. Nonlinear evolution of the out-of-phase dipole gap soliton in the semi-infinite gap with repulsive atomic interactions g=−1 andµ =4.8. The out-of-phase dipole gap soliton corresponds to Fig.6(a).The initial conditions are taken with 1% perturbation in the amplitude and phase to trigger potential instabilities: (a)t=0 and(b)t=100.

Figure 14 shows nonlinear evolution of the out-of-phase dipole gap soliton in the semi-infinite gap atµ=4.8, corresponds to the soliton in Fig.6(a). Figures 14(a)and 14(b)fort=0 and 100 respectively. It can be seen from this figure that the amplitude and position on the lattices of the out-of-phase dipole gap solitons are preserved.The out-of-phase dipole gap soliton is nonlinear dynamical stable. Figure 15 shows nonlinear evolution of the out-of-phase dipole gap soliton corresponding to the semi-infinite gap atµ=5.0.The dipole gap soliton also corresponds to the Fig. 6(a). Figures 15(a) and 15(b)fort=0,100 respectively. It can be seen from this figure that the maximum amplitude and the location of the center of mass versus the evolution timet. During the nonlinear dynamical evolution, the peak amplitude undergoing finite-time collapse, its position on the lattice drift-unstable solitons are typically characterized by“humps”that drift from lattice maxima toward nearby minima. Obviously the dipole gap soliton shows nonlinearly dynamical unstable. That is, in the semiinfinite gap,when solutions near the band have unstable eigenvalue and thus are linearly unstable.Solitons far away from the band have no unstable eigenvalues and thus are linearly stable.However,for all out-of-phase dipole gap solitons show nonlinearly dynamical unstable in the first gap. It can be seen from Fig.7.

Fig. 15. Time evolution of the out-of-phase dipole gap solitons in the semi-infinite gap withµ=5.0,g=−1. The initial conditions are taken with 1% perturbation in the amplitude and phase to trigger potential instabilities: (a)t=0 and(b)t=100.

5. Summary

We have investigated the existence and dynamical stability of multipole gap solitons in BEC loaded in a deformed honeycomb optical lattice. Honeycomb lattices possess a unique band structure, the first and second bands intersect at a set of so-called Dirac points. We find that,when the lattice is gradually deformed, at some strong enough deformation, a gap forms between the first and second bands. We show that the gap in such a deformed lattice can form gap soliton. Both the unipole gap soliton and dipole gap soliton are found. The dipoles can have their bright solitary structures being in-phase or out-of-phase. The linear stabilities and nonlinear stabilities of these gap solitons are investigated.

The stabilities of unipole gap solitons depend on dP/dµ.In the semi-infinite gap,the unipole gap soliton will be stable if its power and eigenenergy satisfy dP/dµ<0, whereas the unipole gap soliton will be unstable if its power and eigenenergy satisfy dP/dµ>0.In the first gap,the unipole gap soliton will be stable if its power and eigenenergy satisfy dP/dµ>0,

whereas the unipole gap soliton will be unstable if its power and eigenenergy satisfy dP/dµ>0. The stabilities of dipole gap solitons are independent of the dP/dµ. For the in-phase dipole gap soliton in semi-infinite gap and the out-of-phase dipole gap solitons in first gap,they are always unstable. For the out-of-phase dipole gap soliton in semi-infinite gap and the in-phase dipole gap solitons in first gap,they are stable far away from the band,while unstable near the band.

Our work provides a qualitative and quantitative guideline towards the more detailed understanding of the possible dynamical features and of the interactions between the coherent structures of strongly correlated states of BEC in 2D optical lattices.