Degenerate asymmetric quantum concatenated codes for correcting biased quantum errors∗
2021-12-22JiHaoFan樊继豪JunLi李骏HanWuChen陈汉武andWenJieLiu刘文杰
Ji-Hao Fan(樊继豪) Jun Li(李骏) Han-Wu Chen(陈汉武) and Wen-Jie Liu(刘文杰)
1School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China
2School of Computer Science and Engineering,Southeast University,Nanjing 211189,China
3School of Computer and Software,Nanjing University of Information Science and Technology,Nanjing 210044,China
Keywords: asymmetric quantum codes,concatenated code,quantum channel,degenerate code
1. Introduction
During the process of quantum computation and communication,[1,2]quantum states are inevitable to be infected by the environment noise from decoherence.[3]Quantum error correction codes (QECCs) are therefore necessary to protect quantum information from decoherence noise due to the environment interactions. Similar to classical error correction codes,how to construct QECCs with good parameters and efficient encoding/decoding algorithms is an important and difficult problem.[4]Although QECCs are highly related to classical error correction codes,the construction of QECCs is not easy at all and it seems more difficult than constructing classical error correction codes. One of the reasons is that there exists an additional dual containing (sometimes called orthogonal) restriction for constructing QECCs. In addition,there exists a striking characteristic in quantum coding theory called error degeneracy, which makes QECCs different from classical error correction codes in principle. It is assumed that degenerate codes have a large potential to correct more quantum errors than nondegenerate codes.[5,6]How to utilize such interesting feature of quantum information to improve the performance of QECCs is a large challenge in quantum coding theory.[4,6]
Recent studies show that quantum noise in many practical quantum channel models is highly biased towards dephasing errors (Z-errors) rather than amplitude errors (X-errors),[7,8]i.e.,there exists a large asymmetry of the happening probabilities forZ-errors andX-errors. In order to take advantage of such important prior information of quantum channels,asymmetric quantum codes (AQCs) are designed and constructed to have a biased error correction ability. For example, in Ref. [9], pure asymmetric quantum maximum-distance separable(MDS)codes with optimal parameters were constructed from two classical MDS codes whose parity-check matrix(PCM) satisfying the orthogonal restriction. In Ref. [10],asymptotically good AQCs were constructed from the dual containing algebraic-geometry (AG) codes. In Refs. [11,12],nonbinary AQCs with a large asymmetry were derived by using nested codes from the Hermitian curve. Recently, biased errors are considered in fault tolerant quantum computation (FTQC)[13,14]and topological codes,[8,15,16]in which the asymmetry can help to improve the fault tolerant threshold largely.
AQCs with a large asymmetry are extremely useful for quantum channels with highly biased noise. As the channel asymmetry is large, theZ-error correction abilities of AQCs become much more dominant. For example, very large performance gains are obtained in the FTQC threshold computation for surface codes by considering biased noise.[8,15,16]But constructing AQCs with a large asymmetry,i.e., a relatively largeZ-distance is quite difficult due to the orthogonal restriction. Recently,several classes of AQCs with big asymmetries were obtained in Ref.[20]by utilizing classical tensor product codes (TPCs)[17,18]and concatenated codes (CCs).[19]However, the authors in Ref. [20] only considered error degeneracy inX-errors, the situation inZ-errors is still unknown. In addition,only binary AQCs with good parameters are explicitly constructed in Ref. [20], the nonbinary case is not given while nonbinary QECCs are of significantly theoretical interest and are important in fault tolerant quantum computation and communication.[5,21]
In this work, we generalize the concatenation scheme in Ref.[20]to a more general case and construct new asymmetric quantum concatenated codes (AQCCs) by considering error degeneracy not only inX-errors but also inZ-errors. Therefore, we can use many existed construction results about degenerate codes,e.g.,[11,12,22]to facilitate our construction. As a contrast,the construction scheme in Ref.[20]only consider error degeneracy inXerrors. Moreover,we give explicit constructions of nonbinary AQCs by using nonbinary constituent codes in TPCs and CCs. It is known that the performance of TPCs and CCs is highly determined by the classical constituent codes. Nonbinary codes over a larger field usually have much better parameters than binary codes. Compared with previous results, our AQCCs can have much better parameters than the existed AQCs in the previous literatures. In special, we use algebraic geometry (AG) codes as outer constituent codes to construct AQCCs and obtain several highly degenerate AQCs which have a large asymmetry.In such case,we show that the pure minimum distance of AQCCs without considering error degeneracy is constant while the true minimum distance is linear to the code length.
We present the general encoding circuit of AQCCs. We show that the amount of quantum gates needed for encoding AQCCs is bounded byO(n1n22+n2n21), wheren1andn2are the code length of the inner constituent code and the outer constituent code,respectively. Compared with the case for encoding general stabilizer codes which is bounded byO(n21n22),our codes need fewer quantum gates for the encoding. Moreover,we the amount of quantum gates of encoding AQCCs can be linear to the block length provided that the corresponding classical constituent codes can be encoded linearly.
2. Theory and construction
We first present some basic knowledge and notations about AQCs, TPCs and CCs. Letqbe the power of a prime numberp. Denote byGF(q)the Galois field which hasqelements and let the fieldGF(qm) be the field extension of the basis fieldGF(q),wherem>0 is some positive integer. Denote by C the complex number field. For a positive integern, denote the Hilbert spaceHn=(Cq)⊗n=Cqnas the tensor product ofncopies of Cq. Aq-ary quantum stabilizer code with parametersQ=[[n,k,d]]qis a subspace ofVnwith the dimensionqk.Qcan detect up tod −1 qudits of quantum errors ford ≥1.
The Calderbank–Shor–Steane (CSS) construction in Ref. [23] is a useful way to derive quantum stabilizer codes from two classical linear codes satisfying the dual containing restriction. Denote bydxanddztwo positive integers. The asymmetric quantum code can be defined as a CSS code with parametersQ=[[n,k,dz/dx]]q, ifQis able to detect anyXerror of weight less thandx,and anyZ-error of weight lessdz.Then AQCs can be constructed from two classical error correction codes whose PCMs satisfying the orthogonal restriction based on the CSS construction.[7,23]
Lemma 1(Ref.[7]Lemma 3.1)
For two classicalq-ary linear codes with parametersC1=[n,k1,d1]qandC2=[n,k2,d2]qwhich satisfy the dual containing restrictionC⊥1⊆C2,there is an AQC whose parameters are given byQ=[[n,k1+k2−n,dz/dx]]q,where

Ifdz=max{d1,d2}anddx=min{d1,d2}, thenQis a nondegenerate code,otherwise it is a degenerate code.
Next we introduce the concept of TPCs and CCs. LetT1=[n1,k1,d1]qbe any classicalq-ary linear code with a PCMHT1. LetT2=[n2,k2,d2]qr1be aqr1-ary code over the extension fieldGF(qr1) with a PCMHT2. Letr1=n1−k1andr2=n2−k2be the numbers of parity checks ofT1andT2,respectively. Denote byCT=T2⊗T T1the TPC ofT1andT2which are the inner and outer constituent codes, respectively.Then we haveCT=[n1n2,n1n2−r1r2]. Map the elements ofHT1fromGF(q)toGF(qr1).HT1can be seen as a 1×n1matrix with elements overGF(qr1). We can obtain an alternative representation ofHT1with size 1×n1. Then the PCM ofCTcan be obtained as the Kronecker product ofHT1andHT2,i.e.,HT=HT2⊗HT1.On the other hand, the PCM of TPCCTcan also be represented by a so-called companion matrix(CM)form in Refs.[24,25],HT=[HT2]⊗HT1,where[HT2]is the representation of a companion matrix ofHT2.
Concatenated codes are obtained by combining an inner codeD1=[n1,k1,d1]qwith an outer codeD2=[n2,k2,d2]qk1over the extension fieldGF(qk1). Denote the concatenation ofD1andD2byCC ≡D2⊗C D1whose parameters are given byCC=[n1n2,k1k2,D ≥d1d2]q. In general,the encoding of CCs can be carried out by the outer encoding and then the inner encoding.[19]Correspondingly, the decoding of CCs is done first by the inner decoding and followed by the outer decoding. But in quantum codes,we have to do the dual containing verification and the syndrome decoding,therefore we need the exact representation generator matrix and PCM of CCs. According to Ref.[25],the generator matrix of CCs can be given in a CM formGC=[GD2]⊗GD1,whereGD1andGD2are the generator matrices ofD1andD2, respectively. The PCM of CCs can be given by

whereHD1andHD2are the PCMs of the inner codeD1and the outer codeD2,respectively.
In Ref.[20],a novel concatenation scheme was proposed to facilitate the construction of AQCs,in which CCs are used for correcting theZ-errors while TPCs are used for correcting theX-errors. Denote byC1=[n1,k1,d1]qany classicalq-ary linear code with a PCMH1and a generator matrixG1. For twoqk1-ary codes over the extended fieldGF(qk1),denote byC2=[n2,k2,d2]qk1and denote byC3=[n2,k3,d3]qk1. Let the PCMs ofC2andC3beH2andH3,respectively,and let the generator matrices of them beG2andG3,respectively.Denote the tensor product code ofC⊥1andC2byCT=C2⊗T C⊥1,and denote the concatenated code ofC1andC3byCC=C3⊗C C1.Then there exists the following result about the construction of AQCs by unifyingCCandCTtogether.
Theorem 1 (Ref. [20]) IfC⊥2⊆C3, there exists a class of AQCs whose parameters are given byQA=[[n1n2,K,dz ≥d1d3/dx ≥d2]]q,whereK=k1(k2+k3−n2).
In Ref.[20],Theorem 1 can be used to derive AQCs with largeZ-distances and efficient decoding algorithms. However,Theorem 1 only considered the error degeneracy phenomenon in the inner codes while the case the case in the outer code was not considered. In this work, we generalize the result in Ref.[20]to a more general situation by considering error degeneracy in both the inner and the outer codes, and we have the following generalized result.
Theorem 2 There exists a class of AQCCs whose parameters are given byQA= [[n1n2,K,dz/dx]]q, whereK=k1(k2+k3−n2),dz ≥d1wt(C3∖C⊥2),anddx ≥wt(C2∖C⊥3).
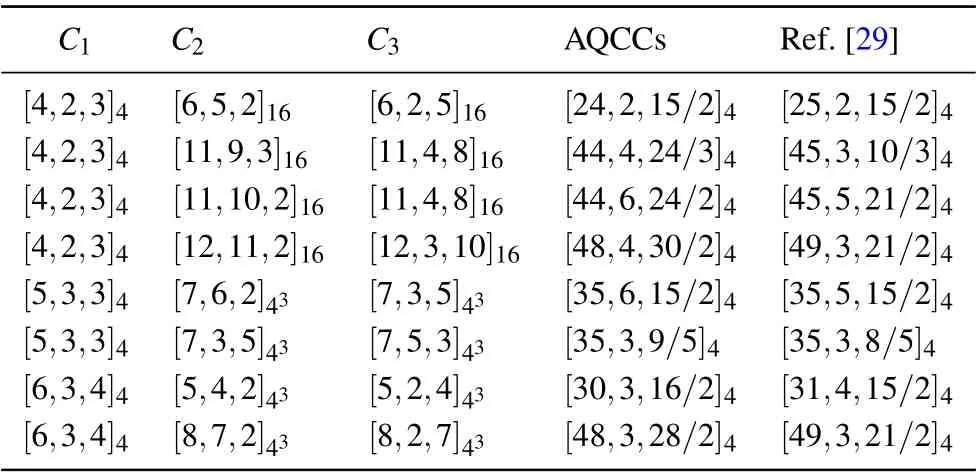
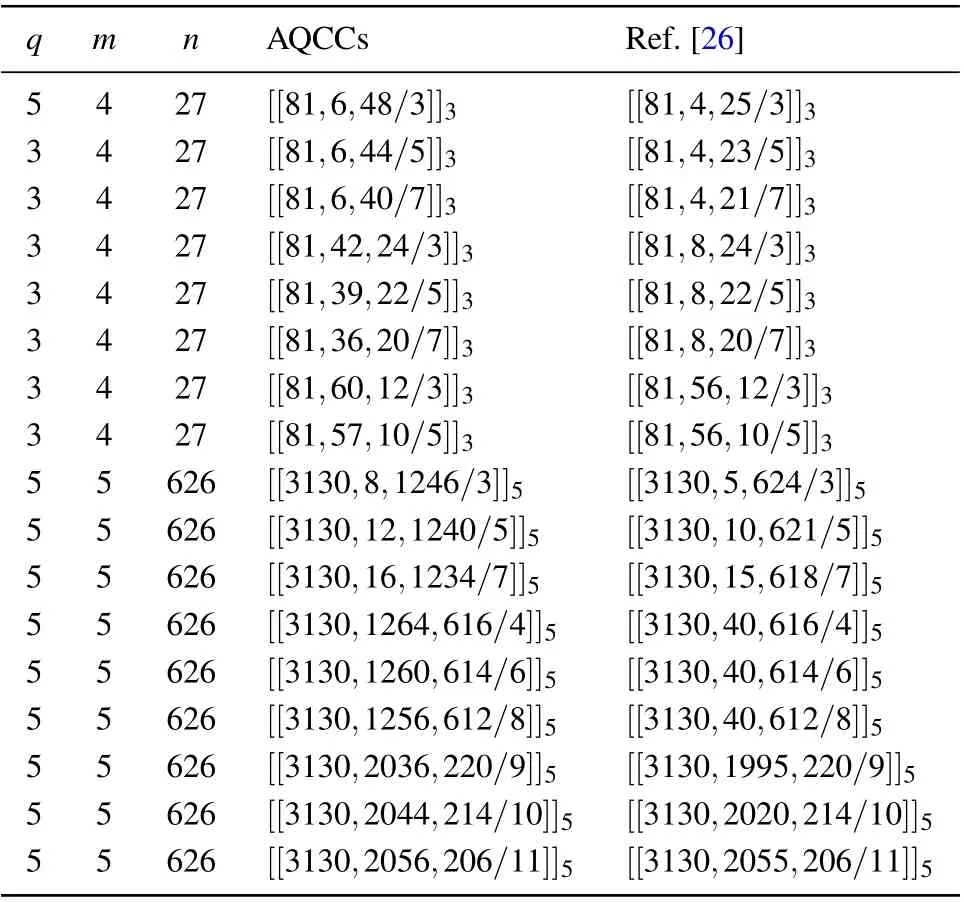
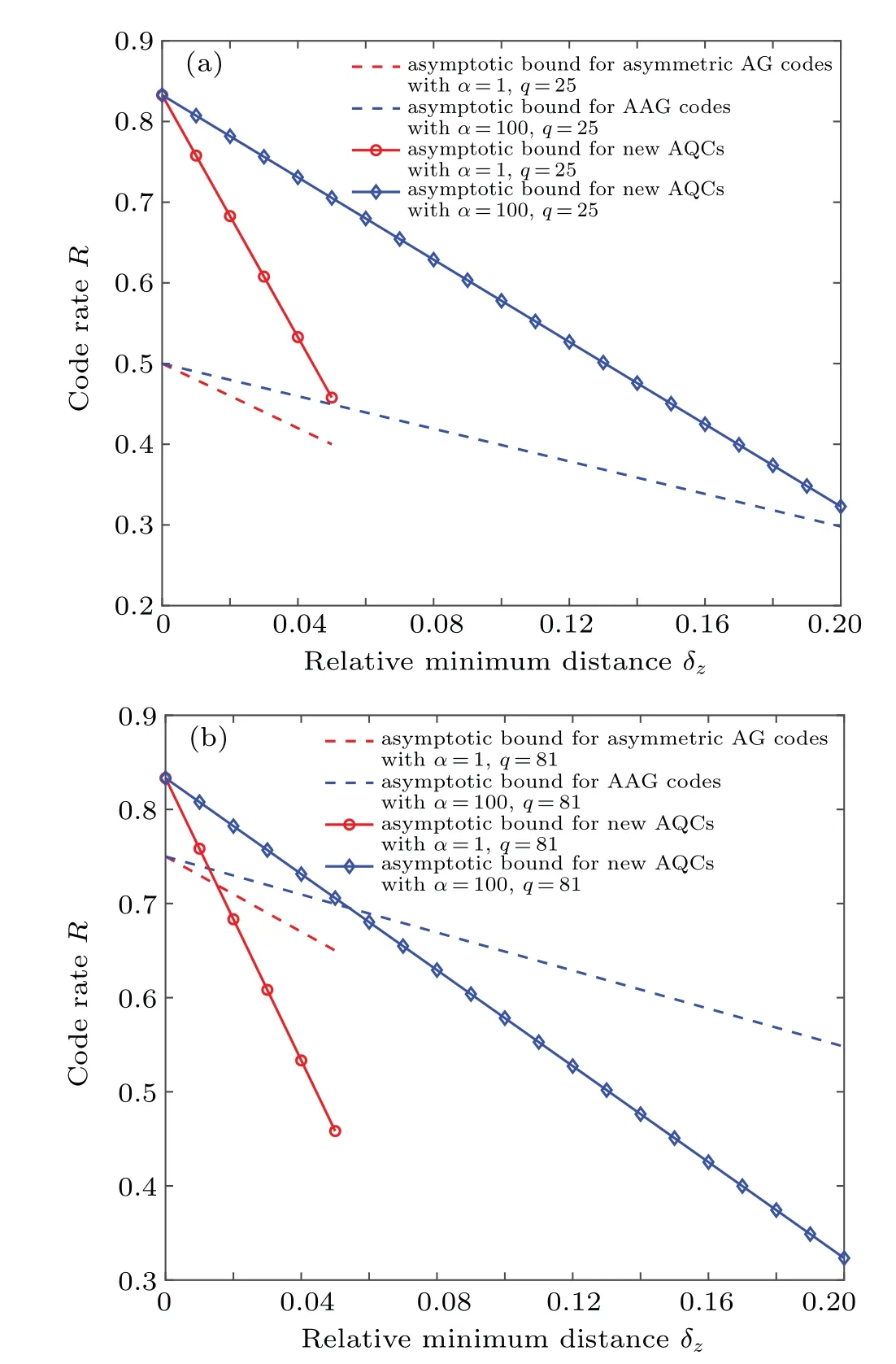
Proof We first compute theX-distancedx. Denote theX-error that happening in the codeword byeX. Similar to the proof of Theorem 1 in Ref. [20], the syndrome informationϒofX-errors is given byϒ=[Ht2]⊗G1·eTX. Denote byϒIi ≡G1eTXi,1≤i ≤n2. ThenϒI=(ϒI1,...,ϒIn2)can be seen as the error sequence happening in the outer constituent codeC2.Then we haveϒ=[Ht2](ϒI1,...,ϒIn2)T,which is the syndrome information for the outer decoding. Suppose that we use some syndrome based decoding algorithm for the outer codeC2to do the decoding and suppose that wt(eX)< wt(C2∖C⊥3).Whatever the errors are separated into different subblocks in the codeword, we must have wt(ϒI) Next we consider the case of correctingZ-errors and compute theZ-distancedz. LeteZbe theZ-error happening in the received codeword and suppose that wt(eZ) Compared to Theorem 1 in Ref.[20],Theorem 2 can have better parameters since we can use degenerate outer codes to do the construction. In Refs.[11,12],several classes of AQCs with big minimum distance are constructed from nested code pairs but those AQCs are unknown whether degenerate or not.Thus the results in Refs. [11,12] were unknown whether can be used to construct AQCs by using Theorem 1 in Ref. [20].We solve this problem by using Theorem 2 and we can use the codes in Refs.[11,12]as the outer codes to construct AQCCs in this work. First, we review some construction results in Refs.[11,12]. Theorem 3 Letl ≥2 be integers and lets ≤q, in whichqis a prime power. Givenδ ∈{1,...,sl}, and letv ∈{0,...,l −1}be such thatsv ≤δ ≤sv+1and choose an integerδ⊥≤⎿(s−δ/sv+1)sl−v−1」. Denote by Proof See the proof of Theorem 24 in Ref.[11]. With the notations given above,we can obtain the the construction of AQCCs as follows. Corollary 1 There is a class of AQCCs with parametersQ=[[n1n2,K,dz/dx]]q,whereK=k1(k2+k3−n2),dz ≥d1δ,anddx ≥δ⊥. In Ref.[11],several classes of nonbinary AQCs with better parameters than the codes in Refs.[26,27]were constructed based on Theorem 3. We takeC1=[n1,1,n1]qas the inner codes and let the outer codes be AQCs listed in Ref.[11]and we construct new nonbinary AQCCs by using Corollary 1. In Table 1, we list the new results and also make comparisons with AQCs in Ref.[26]. It is shown that our new AQCCs have better parameters than the AQCs in Ref.[26]. Table 1. Comparisons of AQCCs with previous works in Ref.[26]. The AQCCs are derived from Corollary 1. It should be noticed that one of the key points to construct highly degenerate AQCCs is by choosing the constituent codesC1with a relatively large minimum distance. Therefore we use some best known nonbinary linear codes in Ref. [28] to construct AQCCs with a large asymmetry,i.e., a large minimum distancedz. For example,we can chooseC1=[5,3,3]4.LetC2=[n2,k2,d2]43and letC3=[n2,k3,d3]43be MDS codes overGF(43), wherek2+k3>n2and 3≤n2≤43+1. Then according to Ref. [4], there isC⊥2⊆C3and then there exist AQCCs with parameters [[5n2,3(k2+k3−n2),3d3/d2]]4according to Theorem 2. Then we can obtain,e.g.,AQCCs with parameters[[35,6,15/2]]4,[[35,3,9/5]]4which are better than[[35,5,15/2]]4,[[35,3,8/5]]4in Ref.[29],respectively. In Table 2, we list more nonbinary AQCCs based on the online codes in Ref. [28]. It is shown that our AQCCs have better parameters than AQCs in Ref. [29]. Table 2. Comparisons of AQCCs with best known AQCs in Ref.[29]. Next,we use the dual of repetition codes which are usually called even weight codes as the inner codes to construct TPCs and CCs.The even weight codes are MDS codes and are thus optimal.We have the following construction of nonbinary AQCCs. Proposition 1 LetC1=[m,m−1,2]qbe the even weight code withm ≥2 andq ≥3 which are integers. There exists a class of nonbinary AQCCs with parameters QE=[[mn,(m−1)(n−d2−d3+2),dz ≥2d3/dx ≥d2]]q,(4) where 2≤n ≤qm−1+1 and 2≤d1+d2≤n+2 are all integers. Proof LetC2=[n,n −d2+1,d2]qm−1andC3=[n,n −d3+1,d3]qm−1be two classical MDS codes over the extended fieldGF(qm−1). If 2≤n ≤qm−1+1 and 2≤d2+d3≤n+2,then there areC2andC3satisfying the dual containing relationship such thatC⊥2⊆C3. According to Theorem 2, there exists a class of AQCCs with parameters [[mn2,(m −1)(n −d1−d2+2),2d2/d1]]q.□ In Ref. [20], binary AQCs constructed from TPCs and CCs were compared with the binary extension of quantum Reed–Solomon (RS) codes. Here we compare nonbinary AQCs in Proposition 1 with nonbinary AQCs obtained from the extension of quantum generalized RS (GRS) codes. In Ref. [26], the following AQCs are obtained from quantum GRS codes with parameters wheredx+dz −2 then our codes have larger dimensions than AQCs in Ref.[26].In Table 3,we list some AQCCs and give detailed comparison between the parameters ofQEandQG. AQCCs show much better parameter performance than the AQCs in Ref.[26]. It is known that classical repetition codes are optimal codes and have the largest minimum distance. If we use classical repetition codes as the inner codes,we can obtain highly degenerate AQCs with largeZ-distances. On the other hand,it is an interesting but difficult problem to determine whether an AQC is degenerate or not.[4]If we use repetition codes as the inner codes,we can easily verify if the resultant AQCC is degenerate. We have the following result about the construction of highly degenerate AQCCs. Table 3. Comparisons of AQCCs with the asymmetric QRS codes.[26]AQCCs are constructed according to Proposition 1. Proposition 2 Letm ≥3 andq ≥3 be integers. Denote byC1=[m,1,m]qthe repetition code which has the largest minimum distance. There exists a class of nonbinary AQCCs with parameters where 2≤n ≤q+1,and 2≤d2+d3≤n+2 are all integers.Further,ifd2≥3,thenQRis degenerate. Proof Denote byC2= [n,n −d2+1,d2]qandC3=[n,n−d3+1,d3]qtwo classical MDS codes over the finite fieldGF(q).If 2≤n ≤q+1 and 2≤d2+d3≤n+2,then there existC2andC3such thatC⊥2⊆C3. Therefore there exists a class of AQCCs with parameters[[mn2,n−d2−d3+2,md3/d2]]q. If we do not consider error degeneracy,then the pure minimum distance ofQRis determined by the minimum of the dual distance ofC1andd2,i.e.,dx ≥min{d⊥1,d2}. Notice that the dual distance of the repetition code isd⊥1=2,then ifd2≥3,the pure minimum distance ofQRwithout considering error degeneracy is always 2. However the true minimum distance ofQRis larger than or equal tod2which is larger than 2.ThereforeQRis degenerate. By using Proposition 2, we can construct nonbinary and highly degenerate AQCCs with a largeZ-distance. We list parts of them as follows: These AQCCs all have a dimension of 1 but theZ-distance is very large. In classical error correction codes,the algebraic geometry(AG) codes can break the classical Gilbert–Varshamov (GV)bound of nonbinary codes when field size is larger than 49.[30]We use nonbinary AG codes with large field size as the outer codes to construct asymptotically good AQCCs. Letq=p2mbe a prime power,wherem ≥1 is an integer. There exists the following construction of asymmetric quantum AG codes in Ref.[10]. Theorem 4(Ref.[10]) Let 0≤δx,δz ≤1 andδx+δz ≤1−2/(pm−1).There exists a class ofq-ary asymmetric quantum AG codesQAsuch that We plot the curves of Eq. (11) in Fig. 1 with different field sizes. It is not difficult to see thatQAis highly degenerate,sincen1is a constant and the dual distance ofC1is also a constant. Moreover, in the binary case, binary AQCs based on TPCs and CCs can only outperform the binary extension of asymmetric quantum AG codes.[20]Here we compare our codes with asymmetric quantum AG codes directly without needing to do the field extension. It is shown that our codes can have better performance than the asymmetric quantum AG codes in Ref.[10]in some scopes,see Fig.1. Fig.1. The asymptotic bounds for our AQCCs in Proposition 3 and the comparison with asymmetric quantum AG codes in Ref.[10]with the field size q=25 and q=81,respectively. It was shown that AQCs in Theorem 1 can be efficiently decodable if the corresponding classical constituent codes can be decoded efficiently.[20]But the encoding of AQCs was not discussed in Ref. [20]. The encoding efficiency of quantum codes is not only important to fault-tolerant quantum computation but also shown to be crucial in fault-tolerant quantum communication.[21]In this section we give the encoding circuit of asymmetric quantum concatenated codes and we use the standard encoding method given in Ref.[31]. Denote the quantum basis state after the encoding by whereOis a zero subblock of size(k3−r2)×r2,Iis an identity matrix of size(k3−r2)×(k3−r2),andP3is a subblock of size (k3−r2)×r3. Then the generator matrix ofCCis given by wherex0is the information bits corresponding tox ∈CC. Assume thatH2andG1are represented by the standard form,i.e.,H2=[I,P2] andG1=[I,P1]. Then we have the general encoding circuit of AQCCs in Fig.2. Now we analysis the encoding efficiency of the circuit in Fig.2. We evaluate the total number of quantum gates in the circuit. In stage I,the number of quantum gates is determined by the density ofP3which isO(n1n22)in the worst case. Similarly in stage II,the number of quantum gates is alsoO(n1n22)in the worst case. While in stage III, the number of quantum gates is determined by the density ofP1and the length of the circuit, and the complexity isO(n2n21). Therefore the total encoding complexity of AQCCs of block lengthn1n2isO(n1n22+n2n21) in the worst case. Compared with the complexity of encoding general stabilizer codes which is given byO(n21n22),our codes have a lower encoding complexity. Moreover,it is easy to see that if the classical constituent codesC1,C2, andC3can be encoded efficiently in linear time, for example,P1,P2, andP3are with low density, then the encoding complexity of AQCCs isO(n1n2). Thus AQCCs can also be encoded efficiently in linear time provided that the constituent codes are efficiently encodable. Fig.2. The encoding circuit of asymmetric quantum concatenated codes. In stage I,the block labeled by )(1 ≤i ≤n2)means that the qubits pass it are controlled by a qubit in quantum state|ψ〉. If there is a“1”in the j-th position of the i-th row of P3,then there is a C-NOT target“⊗”in the j-th quantum state of the subblock,i.e.,each)corresponds to a row of. Similarly,each )(1 ≤i ≤r2)in stage II corresponds to a row ofand each )(1 ≤i ≤in stage III corresponds to a column of[P1]. We give an explicit example to illustrate the encoding of AQCCs. LetC1=[3,2,2]be the even weight code. LetC2,C3be two 4-ary codes with parameters [5,3,3]4and they satisfyC⊥2⊆C3.[32]The generator matrix and the PCM ofC1are given by The generator matrices and PCMs ofC2andC3are given as follows: whereαis the primitive element ofGF(4). It is easy to verify thatH2HT3=0.Then we can obtain an AQCC with parametersQ=[[15,2,6/3]]. The generator matrixG3is equivalent to the following one under some elementary row transformations: The elements 0,1,α,α2ofGF(4) can be represented by the companion matrix form of the primitive polynomialf(x)=1+x+x2as follows(see Refs.[24,25]): Then the encoding circuit of this code is given in Fig.3. Fig.3. The encoding circuit of the AQCC[[15,2,6/3]]. In this paper, we constructed new families of AQCCs based on the concatenation scheme by utilizing error degeneracy of quantum codes. We made detailed comparisons between our new codes and previous AQCs,and showed that our codes can have a better performance than previous ones. Several families of highly degenerate AQCCs with a large asymmetry were deroved. We gave the general encoding circuit of AQCCs and showed that the number of quantum gates needed to encode our codes is lower than that of the general stabilizer codes. Our codes are practical to the future quantum information processing systems[33,34]with highly biased errors.






3. Encoding circuits of asymmetric quantum concatenated codes
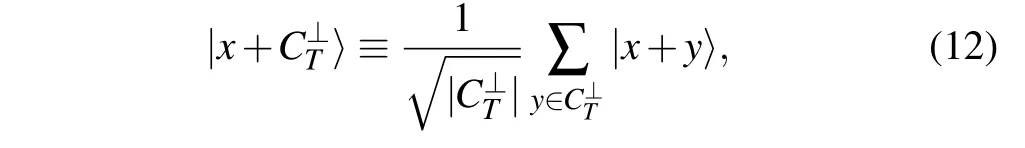
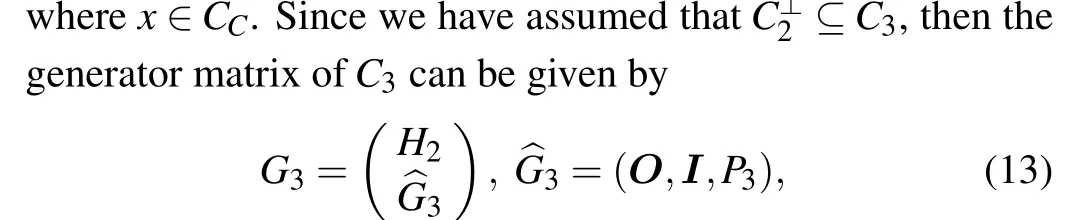









4. Discussion and conclusions
杂志排行
Chinese Physics B的其它文章
- Transient transition behaviors of fractional-order simplest chaotic circuit with bi-stable locally-active memristor and its ARM-based implementation
- Modeling and dynamics of double Hindmarsh–Rose neuron with memristor-based magnetic coupling and time delay∗
- Cascade discrete memristive maps for enhancing chaos∗
- A review on the design of ternary logic circuits∗
- Extended phase diagram of La1−xCaxMnO3 by interfacial engineering∗
- A double quantum dot defined by top gates in a single crystalline InSb nanosheet∗
