Geological Guided Tomography Inversion Based on Fault Constraint and Its Application
2021-12-22LISanfuZHANGXiaoboDANZhiweiSUNBoSONGPengSUNLeimingFANGZhongyuandLILie
LI Sanfu, ZHANG Xiaobo, DAN Zhiwei, SUN Bo, SONG Peng, SUN Leiming, FANG Zhongyu, and LI Lie
Geological Guided Tomography Inversion Based on Fault Constraint and Its Application
LI Sanfu1), ZHANG Xiaobo2), 3), 4), 5), *, DAN Zhiwei1), SUN Bo1), SONG Peng4), SUN Leiming1), FANG Zhongyu1), and LI Lie6)
1),,524057,2),,266061,3),,266590,4),,266100,5),,266237,6).,524057,
Fault block reservoirs are one of the main types of hydrocarbon reservoirs found in offshore basins, and they are widely distributed within the Mesozoic and Cenozoic basins of the northern South China Sea. Conventional seismic profiles of complex fault areas often contain obvious fragmentation and distortion of seismic events that is corresponding to geological structure under the fault. This phenomenon is known as a fault shadow; it occurs in relation to rapid changes in velocity near the fault that deviate the ray path of waves, and it seriously affects the ability to determine the geological structure and subsequently evaluate the reserves of fault reservoirs. In the current conventional tomography inversion method, the velocity model is over-smoothed, which results in distortion of the reflection layer under the fault. Based on the velocity tomography inversion of imaging gathers method and the concept of regularization, this paper first introduces the anisotropy Gauss regularization operator. A high-resolution tomography inversion method is then developed, and the fault-controlled geological guidance is constrained. This technology is then applied to a complex fault block reservoir basin in the South China Sea, and the results show that it can significantly solve the problem of fault shadow imaging and determine the geological structures in the target area. The newly developed method thus has very good application prospects.
fault block reservoir; fault shadow phenomenon; geological guidance-constrained tomography; regularization; pre- stack depth migration
1 Introduction
As one of the main types of hydrocarbon reservoirs in offshore basins, fault block reservoirs are widely distri- buted in the Mesozoic and Cenozoic basins of the northern South China Sea. Such complex fracture systems are formed in basins under the action of compression and ten- sile stress, and the stratigraphic velocity changes dramatically between fault blocks, particularly at fault junctions. In complex fault blocks that have undergone small-scale changes, the stratigraphic velocity on both sides of the faultblock is often affected by compaction, lithology, fluid, and other factors, and there are rapid lateral velocity changes. Conventional seismic profiles of complex fault areas often show the existence of fault shadows, which are characterized by poor illumination and the false structural re- presentation of sub-fault seismic reflection data, and they relate to distortion of the seismic events that is correspond- ing to geological structure and weakening of the amplitude in the footwall area of the fault. Both Fagin (1996) and Trinchero (2000) defined and described fault sha- dows and determined that a drastic change in lateral velo- city that deviates the ray path of waves is the primary factor relating to their occurrence.
Conventional velocity inversion and modeling methods are mostly based on simple structures or a slowly changing velocity hypothesis. For example, conventional velo- city analysis methods based on CRP gather provide an ex- tremely low prediction accuracy under complex fault blockconditions and strong laterally variable velocity media. This makes it difficult to obtain accurate images of fault blocks and even leads to the construction of distortion traps, whichultimately makes exploration and evaluation risky. Pre- stack depth migration has become a common method used to obtain images of complex structures during hydrocarbon seismic exploration, where accurate migration velo- city inversion and modeling are keys to determining the quality of pre-stack depth imaging. Nevertheless, tomography inversion remains the most commonly used velocity modeling method in the petroleum industry, and it is basedon the mechanism of flattening seismic gathers at the same imaging point but at different angles (or offsets). In tomography inversion, the quality of the imaging gather, automatic picking of the residual moveout, picking of the inclination at reflection interface, ray tracing to establish the tomography matrix equation, and the solution of large- scale matrix equation are factors that affect the inversion results (Zelt and Smith, 1992).
To improve the inversion accuracy, Chapman and Pratt (1992) used linear perturbation theory to determine the travel times in weakly anisotropic media, with the aim of discussing the dependence of travel times in 2-D cross-hole tomographic experiments on the anisotropic parameters. Yang. (2008) achieved construction of an accurate macro velocity depth model using automatic picking of travel-times and the gradient for a local slant stack. Furthermore, Qin. (2012) proposed an image domain tra- vel-time tomography velocity inversion method that uses angle domain common imaging gathers (ADCIGs) as the gathers for the velocity analysis and obtains the accurate travel-time residual using an automatic fitting picking stra- tegy of residual curvature.
However, velocity tomography inversion that does not include sufficient regularization constraints is only able to produce a smooth background version of the velocity field,and it fails to obtain dramatic velocity changes on both sides of the fault block. Such velocity models can only meet the imaging requirements of large-scale reflective formations, and the accuracy is insufficient for small-scale fault blocks that have rapid lateral changes.
It is thus necessary to introduce suitable regularizations for velocity inversion and modeling to improve the accuracy of velocity modeling (Lu., 2005; Ohdachi., 2019). Even the most advanced reflection full waveform inversion (Wu and Alkhalifah, 2015; Zhou., 2015; Yao and Wu, 2017; Wang., 2019; Yao., 2020) requires a sufficient regularization method (Yao., 2019) to obtain accurate velocity estimation results of small- scale geological bodies (Tarantola, 2004; Liu., 2020). In this respect, Gochioco. (2002) and Birdus (2007) discussed a method that introduces pre-stack depth migration technology based on accurate velocity modeling to solve the fault shadow phenomenon. Hart. (2015) and Rodriguez. (2011) then added geological structure information to control the building velocity, with the aim of improving the accuracy of the velocity model, and to a certain extent, this assisted in solving the fault shadow problem in some areas, such as the Barents Sea in northern Europe.
In this paper, we introduce an anisotropic Gauss regularization operator and use the regularization principle to develop a high-resolution tomography velocity inversion method based on the constraints of fault-controlled geolo- gical guidance. Compared with the conventional tomography method, this method effectively improves the accuracy of the velocity model within complex fault block areas and the quality of seismic imaging in the depth domain. The successful application of using this technology is verified by using it to process a complex fault block re- servoir in the northern South China Sea.
2 Principles of Imaging Gathers’ Travel Time Grid Tomography Inversion
In the petroleum industry, the most commonly used reflection wave velocity tomography inversion method is based on the travel time grid obtained from imaging ga- thers (Cheng., 2002; Woodward., 2008). It esta- blishes the inverse problem of velocity tomography based on flattening the gathers. At the same time, the velocity inversion results that flatten the imaging gathers can get the best focused migration imaging results (Zhang and Wang, 2019; Zhang., 2019).
Velocity tomography inversion in angle domain common imaging gathers is used to simulate the travel path of seismic wave at all angles or offsets. It is based on the slowness perturbation hypothesis in the initial slowness field, and the residual time difference of the same imaging gather along the ray path is updated to derive a slowness update value (Zhang, 2011). The rationale of ray tomogra- phy is shown in Fig.1.

Fig.1 Ray path diagram of inclined complex medium.
S is the source point, R is the corresponding receiver point, A is the imaging point of the migration velocity, Ais the migration position at the same velocity, AB point is the pickup residue depth difference, and,are the angle of incidence of the migration ray path and the dip angle of the layer, respectively. The red line is the position of the common imaging point (CIP), the solid line SAR is the tracing path of ray at incorrect migration velocity, and the dashed line SAR is the path of ray at the assumed true velocity. The two are equal in total travel time, but the imaging positions are inconsistent.
According to the principle of equal travel time (equi- valent to the linearization hypothesis defined in Eqs. (A-2) to (A-4) of Appendix, which supposes that the initial velocity field is correct and the estimated velocity perturbation is small), the following equation can be established,
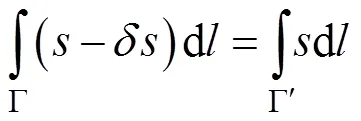
where s is the true slowness,is the slowness perturbation, Γis the true velocity ray path, which is unknown; and Γis the migration velocity ray path, which can be obtained by ray tracing.
Eq. (1) can be transformed into
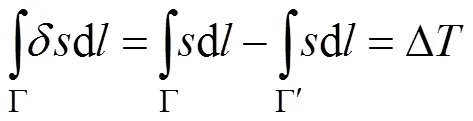
whereis the required slowness correction, and the term on the right side is the residual time difference, ∆.
The pre-stack depth migration can provide CIP gather in the depth domain, which is generally not flattened within a certain imaging depth difference (the depth difference between the result of true velocity imaging and the result of migration velocity imaging) at each angle or migration. To establish the relationship between the residual time difference, ∆, and the residual depth, ∆, the reflection point in Fig.1 is partially enlarged, as shown in Fig.2. Near the reflection point, the slowness, can be assumed to be constant. As the two ray paths situated away from the reflection point are close to each other, the time difference caused by them can be considered to be zero. Thus, at the reflection point, the term on the right side of Eq. (2) is the difference between the two ray paths multiplied by the slowness,, which is,
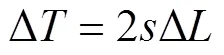
where ∆=∆coscos, ∆=AB, andis the slowness of the local point. Eq. (3) can also be expressed as
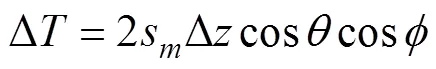
By substituting Eq. (4) into Eq. (2), the relationship be- tween the residual depth difference and the slowness perturbation quantity is obtained,
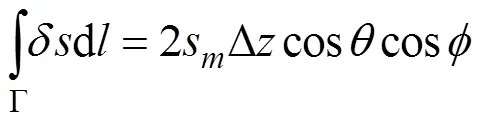
In this way, each pickup residual depth difference, ∆, is matched with a certain ray path, and an equation is established. In the numerical calculation, the term on the left side of Eq. (5) is discretized, and the following formula is thus obtained,

where ∆sis the slowness perturbation quantity of the-th grid point, andlis the ray length of the ray in the-th grid. The underground space for inversion is discretized and forms in a total ofgridgrid points, and all shots and receivers and underground reflection points correspond torays, thus forming×gridlarge sparse matrixes. The tomography matrix equation is

where L is the coefficient matrix and its elements are the ray paths of each ray in each velocity grid; ∆s is the slow- ness correction vector; and ∆T is the residual time difference vector. Therefore, the inverse problem of ray tomography becomes an iterative linear problem, and by solving sparse equations, the slowness or residual slowness, ∆si is ultimately obtained in Eq. (7).
Velocity tomography inversion and modeling in angle domain common image gathers are performed according to the above theoretical framework (Xu, 2006). How-ever, the quality of the velocity tomography inversion results is controlled by many factors, such as the accuracy of travel time pickup, the ray tracing accuracy, the estimation accuracy of the reflection inclination, and the spatial distribution and sampling of shots and receivers. In practical application, the most important consideration in solving the actual velocity modeling is how to impose regularization constraints on the model.
3 Fault-Constrained High-Resolution Tomography Inversion Method
Mathematically, to obtain velocity updates in tomogra- phy velocity inversion, it is necessary to solve large-scale sparse linear equations, such as Eq. (7) (Yang, 1997). Eq. (7) presents a linear positive problem that establishes the mapping relationship from the model space to the data space, and it can be written abstractly as=orobs≈. This large-scale sparse matrix equation is generally underdetermined (Zdraveva., 2013), and both the ori- ginal equation and the normal equation based on the least squares are not of full rank, which leads to multiple solutions. In addition, the description or expression of the velocity field can seriously affect the properties of the solution. Certain constraints on the model parameters are there- fore required to obtain a stable, high-precision, geologically significant, inversion solution when practically applying tomography inversion and modeling methods, and regularization of an inverse problem needs to be solved. Tikhonov’s regularization method is based on Bayesian estimation theory, and it is the classical method used in this respect. Under this theoretical framework, we pro- pose the following posterior probability density maximization method as the model parameter estimation method.
The posterior probability density function is
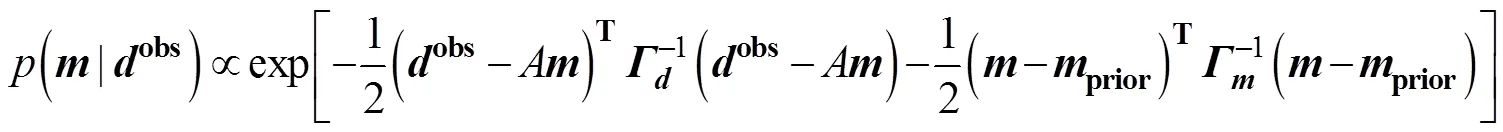
whereprioris the prior model parameter;represents the data covariance matrix, andis the model parameter covariance matrix. Superscript ‘−1’ denotes the inverse of the matrix, and superscript ‘T’ denotes the transpose of the matrix. The inversion solution of model parameters corresponding to posterior probability maximization is

The optimal inversion problem with posterior probabi- lity maximization is obviously equivalent to the following problem of minimizing the cost functional,

and
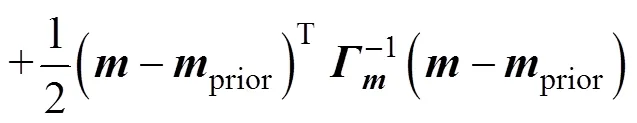
This is called a cost function or error functional, and the first term in Eq. (11) is the data deviation term and the second term is the penalty function term, which is also known as the model parameter constraint term or the regularization term.
In inversion theory, the above equation is more widely known as the Tikhonov regularized linear inversion method, and it can be written as
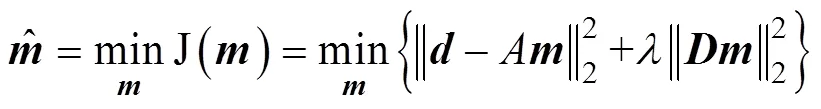
The meanings of the two terms in Eq. (12) are the same as those in Eq. (11), and in the formula, matrixis an appropriate operator applied to the model parameters. To satisfy both the penalty function term and the theoretical requirements of Gauss distribution, the appropriate operator is often a first-order difference operator.
The normal equation corresponding to Eq. (12) is
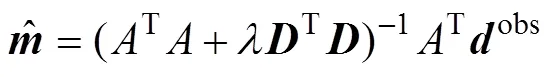
and after the introduction of the penalty function, whether the normal equation is of full rank can be determined by the coefficient,, of the penalty function. However, although the physical meaning of introducing a penalty function in this way is clear, selectingis difficult in the practice of seismic survey inversion.
Penalty functions can be defined using many different forms. For example, the penalty function in Eq. (12) can be written in a general form,
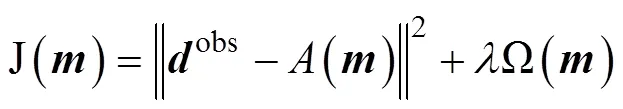
and typical penalty functions are listed as follows:
the classical square regularization method,

the sparse regularization method,

total variation regularization,

and combination regularization,

The regularization form selected is closely related to the specific situation of the model to be inverted. For example, Eq. (15b) is suitable if the reflection coefficient is to be inversed, because the reflection coefficient is sparsely distributed. However, Eq. (15c) is suitable if the velocity or slowness is to be inversed, because the speed or slowness appears to be relatively uniform within the layer or block.
For inversion methods used in seismic exploration, it is necessary to reasonably integrate geological information into the inversion results. Therefore, a so-called geological constraint regularization method is proposed (Clapp., 2004), the basic premise of which is to incorporate structural information about the reflection interface as the constraint information into the inversion process.
In addition, a very important regularization principle is to transform some of the parameters prior to inversion, and transformation of the model parameters is thus introduced,

whereis a feature transformation operator for model parameters, and is a type of smooth convolution operator; therefore, onlyincludes the smooth part of the model parameters. In this respect, conventional inversion theory shows that inversion of the smooth part of model para- meters is more robust and convergent.
The Tikhonov regularized inversion function of the mo- del parameters in the original domain is
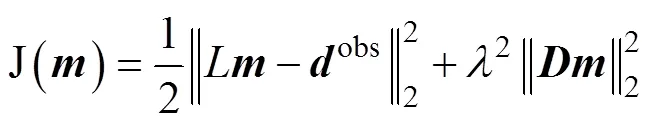
and in the transform domain is
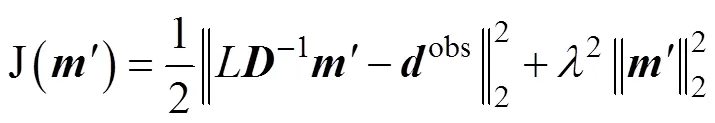
and their corresponding normal equations are
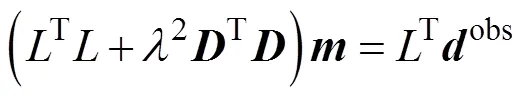
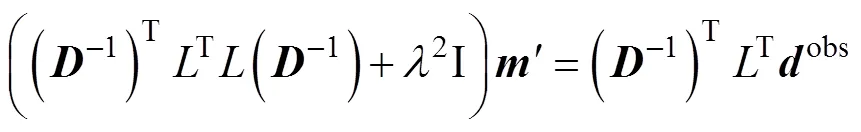
respectively, where Eqs. (18a) and (18b) are obviously completely equivalent.
The meanings of the two tomography inversion solutions in the original domain and the transform domain can be described as follows. In the Tikhonov regularization inversion of the original domain, operatorin Eq. (17a) is a rough operator, and it is generally selected as the Laplace operator. In the Tikhonov regularization inversion of the transform domain, operator−1 in Eq. (17b) is the rough operator, and it is generally selected as the Gauss operator.
The geophysical implications of operatorassociated with regularization can be seen more clearly by the error functional (Eq. (11)) defined by posterior probability. The matrix,, is the model parameter covariance matrix, and this is a convolution matrix or smooth matrix. Its inverse matrix,−1, is of course a deconvolution matrix or a roughing matrix. The prior information constraint under the Bayes theory defined by Eq. (11) is more basic, and the regularization methods of other variants are derived from Eq. (11). This explains clearly why the rough operator (La- place operator) is taken in Eq. (17a), and the smooth operator (Gauss operator) is taken in Eq. (17b).
A basic and reasonable regularization idea is to reasonably integrate geological information into the inversion results in the tomographic inversion when conducting seismic exploration. Therefore, we propose a fault constrained velocity tomography inversion method. Based on the above tomography inversion regularization principle, and introducing the anisotropy Gauss weighting operator and the variation trend of the velocity field on both sides of the fault into the tomography inversion equation, the precision of velocity tomography inversion in complex faultblocks can be effectively improved (Zhou., 2009; Zhou, 2013).
In this respect, assuming that the objective function is J(), the inversion objective function with information about the fault and the geological structure is as follows,
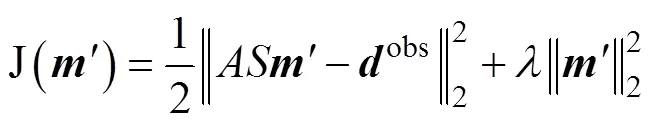
On the right side of Eq. (19), the first term represents the RMO residual of the unleveled imaging gathers, and the second term is the regularization term for the geological constraint. In addition, the constraints of the fault and reflector structure on the velocity tomography inversion are specified by the regularization operator,. To highlight the structural information of the fault and reflected layer in the velocity inversion results,should be chosen as the anisotropic Gauss operator.
The anisotropy Gaussian operator in a three-dimensional space is
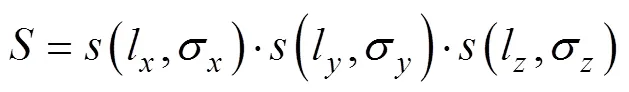
and the Gaussian operator in one-dimension is

whereis the distance parameter between the current point and the processing point, ands the standard deviation. Variations in the standard deviation in different directions illustrate why it is necessary to impose constraints based on the geological structure.
The core issue in velocity tomography inversion is to determine an appropriate anisotropic Gauss regularization operator,. To adapt the smooth operator to the direction of the formation structure,needs to be rotated three-di- mensionally along the tectonic direction. Assuming that the inclination of the formation isand the azimuth is, then two rotation matrices,and, can be constructed. The regularization operator after rotation is expressed by Eq. (22a), which further realizes the regularization constraint under geological guidance,

where
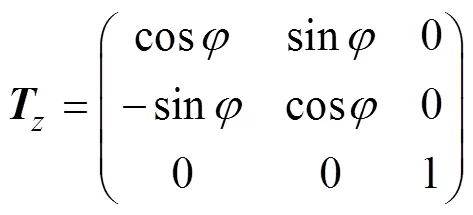
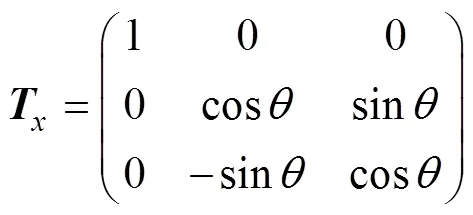
By constructing an appropriate anisotropic Gauss operator,, and substituting it into the corresponding normal equation of Eq. (28), the following can be obtained,

In this paper, the least square conjugate gradient methodis employed to solve Eq. (19) (Zhdanov, 2002). In this respect, the initial model parameters are first given. According to the objective function, J(), in each iteration, the gradient direction and iteration step length of the model parameters,, are obtained through modeling and data processing, and these are used to update the model parameters. After multiple iterative inversions, the extreme value of the objective function, J(), will be minimized.
We conducted simple numerical experiments to prove the correctness of the above theoretical analysis, and we present here a comparative analysis based on the two-di- mensional fault model shown in Fig.3a. Fig.3b is a conventional tomographic operator with a Tikhonov’s regularization operator (Eq.17(a)); the operator only considers the horizontal and vertical weighting constraints, and the inversion results cannot reflect the trend of the inclined formation structure. However, Fig.3c is a geological gui- dance-constrained tomography operator. The essence of this algorithm is to design a Gaussian regularization operator (Eqs. (19) to (23)) along the structural dip angle. The connection between the adjacent slowness update in the structural direction is established by Gaussian weighting, andthe slowness updates with structural characteristics are thenobtained by inversion. The advantage of this method is that it considers the dip angle of the formation, and the characteristics of the formation structure trend are well reflected, but it still cannot solve the problem of the abrupt velocity change at the fault block.
However, the fault-controlled geological guidance tomography (Fig.3d) proposed in this paper further adds fault boundary constraints based on the tomography. By setting the fault boundary control in the model space, the Gaussian regularization operator is truncated at the fault boundary, which guarantees the abruptness and variation in velocity on both sides of the fault block. The fault boundary information is obtained by interpretation of the 3D migration data volume and is then processed by gridding and data interpolation, and finally input into the tomography algorithm in the form of a mask volume. The problem of velocity trend stability and velocity abruptness in the model space is effectively solved by controlling the geological guidance constraints, and the parameter results reflect the characteristics of both the geological structure trend and the abrupt velocity changes on both sides of the fault.
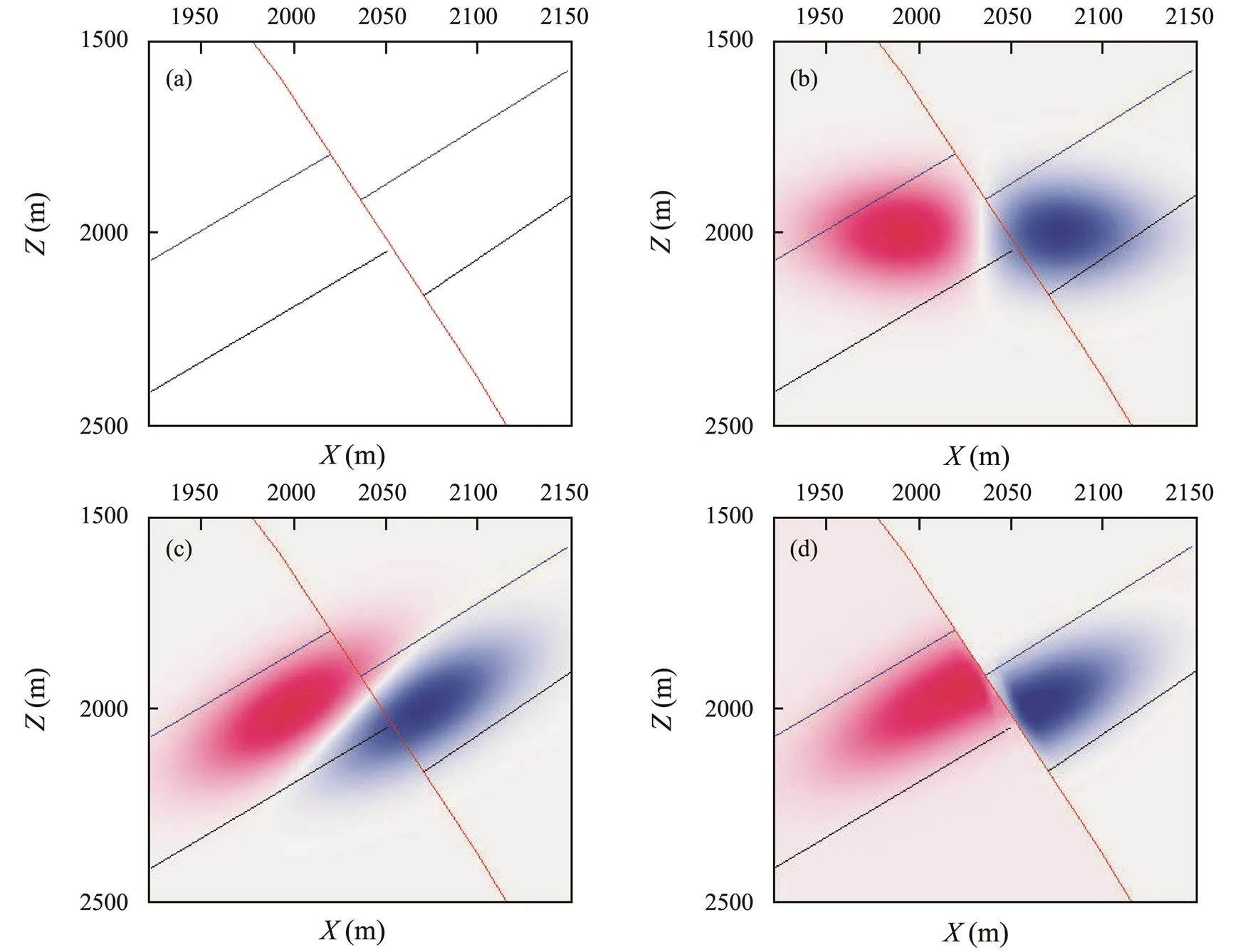
Fig.3 Comparison between tomography regularization operators. (a), fault model; (b), conventional tomography; (c), geological guidance-constrained tomography; and (d),fault-controlled geological guidance-constrained tomography.
The above operator comparison shows that by constraining the spatial distribution characteristics of the model parameters with the underground structural information in seismic tomography inversion, and by adding the information to the tomography inversion based on the Tikhonov model regularization or pre-condition principle, the geological rationality and accuracy of model parameter estimation can be effectively improved.
4 Theoretical Model Test
To verify the effectiveness of the method, a fault block geological model with a length and depth of 15000m and 5200m, respectively, was designed (see Fig.4a). The theoretical shot gather data were obtained based on the forward modeling by solving wave equations with the finite difference method. The parameters of the simulation observation system were collected: a shot interval of 50m, receiver interval of 25m, CDP interval of 12.5m, receiver array length of 5000 m, and a total shot number of 300. To effectively evaluate the applicability of each tomography method, we extracted a seismic trace at each end of the model for spatial linear interpolation to establish a baseline initial velocity model for the inversion test (see Fig.4b). Based on the depth-domain gathers obtained by the Kirchhoff depth migration of the initial velocity model, we then compared the conventional tomography inversion and tomography inversion control tests. Figs.4c and 4d show velocity updates of the final iterations from conventional tomography inversion and the method proposed in this paper, respectively, and Figs.4e and 4f show the updated velocity model obtained after conducting the above inversion process using the two methods, respectively.
As shown in Figs.4c and 4e, the conventional method is unable to effectively inverse the boundary of fault velocity and changes on both sides of the fault blocks, and the inversion results have a low accuracy. In addition, the inversion parameters update values have obvious projection illusions of the ray path due to the lack of effective geological regularization constraints.
However, Figs.4d and 4f show that by introducing constraining information about the fault structure, the proposed method effectively inverts the change in the velocity of the formation on both sides of the fault block (shown by the position of the arrow in Fig.4d), and effectively re- stores the structural characteristics of the formation in the velocity model. In addition, compared with conventional methods, the method proposed in this paper can achieve velocity inversion in deeper formations. By using this process, the vertical and horizontal resolution is significantly improved; therefore, the correctness of the method is verified.
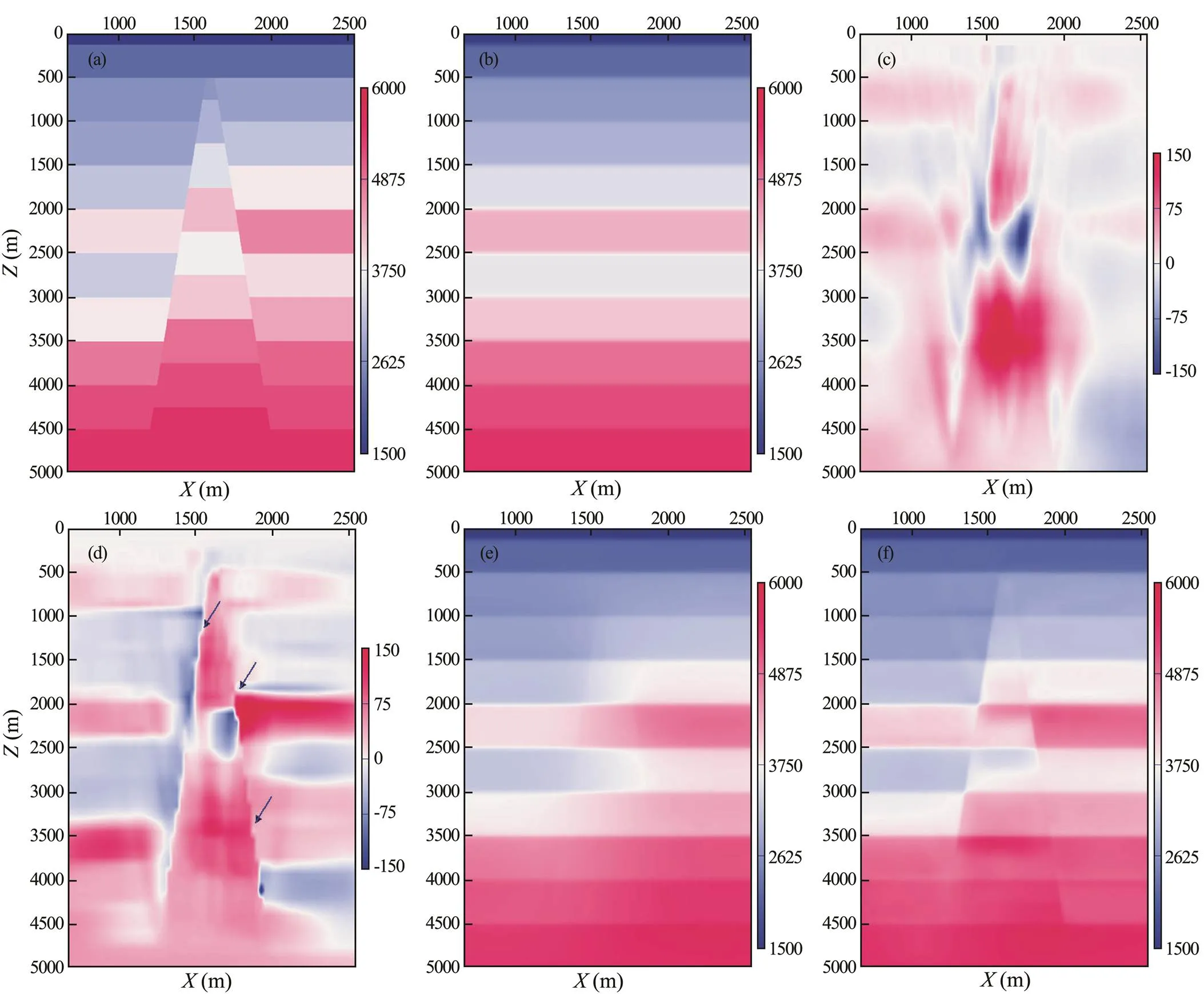
Fig.4 Fault block geology model and comparisons between different tomography methods. (a), fault geology model; (b), initial velocity model; (c), updated values from conventional tomography; (d), updated values from fault-controlled geological guidance-constrained tomography; (e), velocity updated model obtained by conventional tomography; and (f), velocity updated model obtained by fault-controlled geological guidance-constrained tomography.
5 Real Data Processing
To verify the real processing capacity of this method, we conducted an application test in a complex fault block basin in the South China Sea. The geological reservoir accumulation conditions in this area are superior, the exploration potential is great, and fault zones are the most favorable exploration targets. However, shadow phenomenon occurs prolifically in seismic faults in this area, due to the complex fault structure. As shown in Figs.5a and 7a, the seismic reflection structural characteristics of the target formation are unclear because of the seismic fault sha- dow; the seismic events are broken and the seismic structures are distorted. This causes great uncertainty in evaluations of the trap and reservoir. Using the proposed method, we conducted tomography inversion for this area and then compared the results with those obtained using conventional tomography methods. The PSDM images reported in this section are processed using the Kirchhoff migration module in Paradigm. Figs.5a and 5b show the profiles of PSDM images overlaid on the migration velocity that were obtained using conventional tomography inversion and the proposed tomography inversion, respectively; Figs.6a and 6b show the local profiles of PSDM images overlaid on the velocity updates obtained using the conventional tomography inversion and the proposed tomography inversion, respectively; and Figs.7a and 7b show slices of PSDM images overlaid on the migration velocity obtained by the conventional tomography inversion and the proposed tomography inversion, respectively. The dots in the figures represent the locations of well points, and the different colored curves on the slice represent the projection of fault interpretation data. The comparisons show that although the conventional method reflects the slight change in velocity at the fault block, the background is too smooth. In contrast, the proposed method greatly improves the velocity resolution and accuracy both vertically and horizontally by introducing the regularization constraint of the fault control geological structure in the inversion operator. Moreover, the geological structure trend of the velocity model is more consistent, and the velocity changes on both sides of the fault block are clearly described.
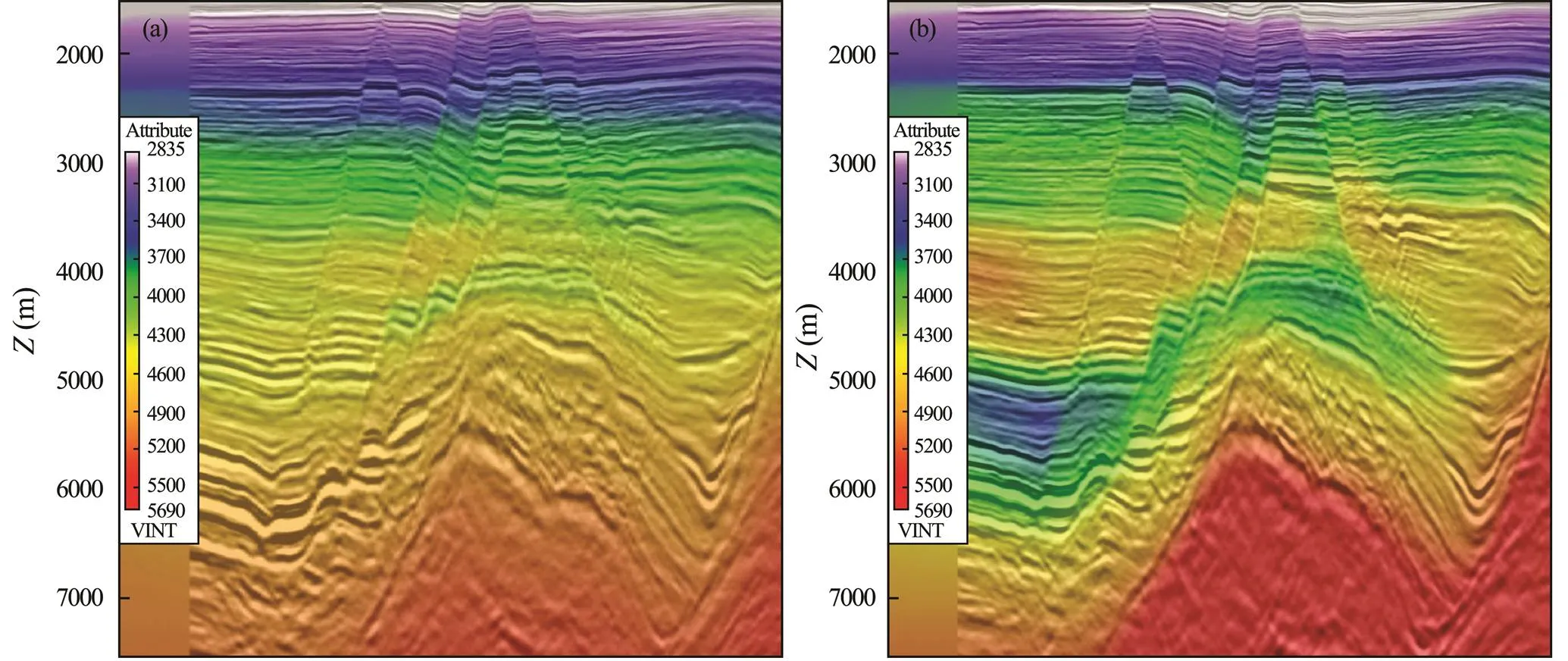
Fig.5 Profiles of PSDM images overlaid on the migration velocity. (a), conventional tomography; (b), fault-controlled constrained tomography.
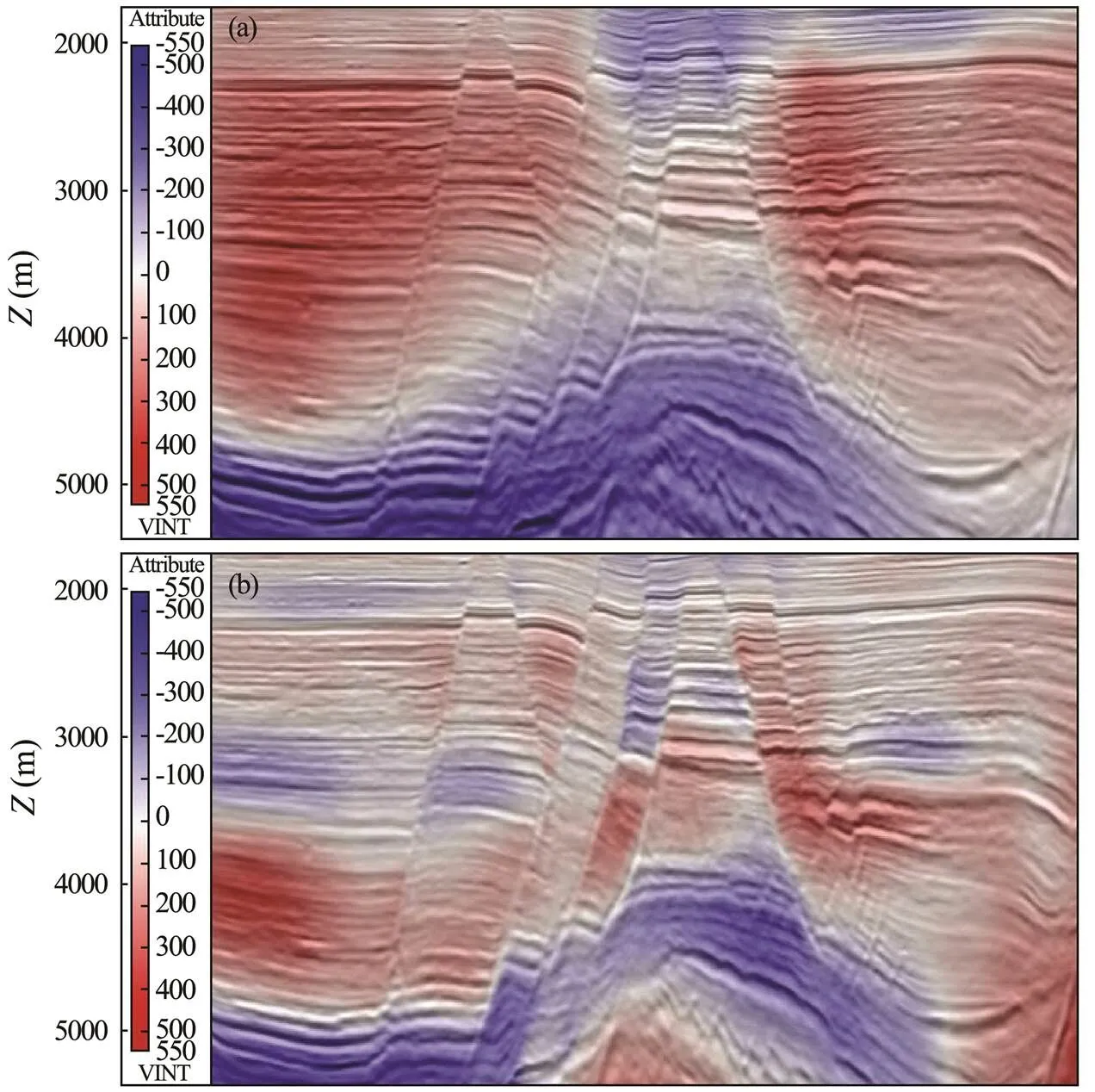
Fig.6 Local profiles of PSDM images overlaid on velocity updates. (a), conventional tomography; (b), fault-controlled constrained tomography.
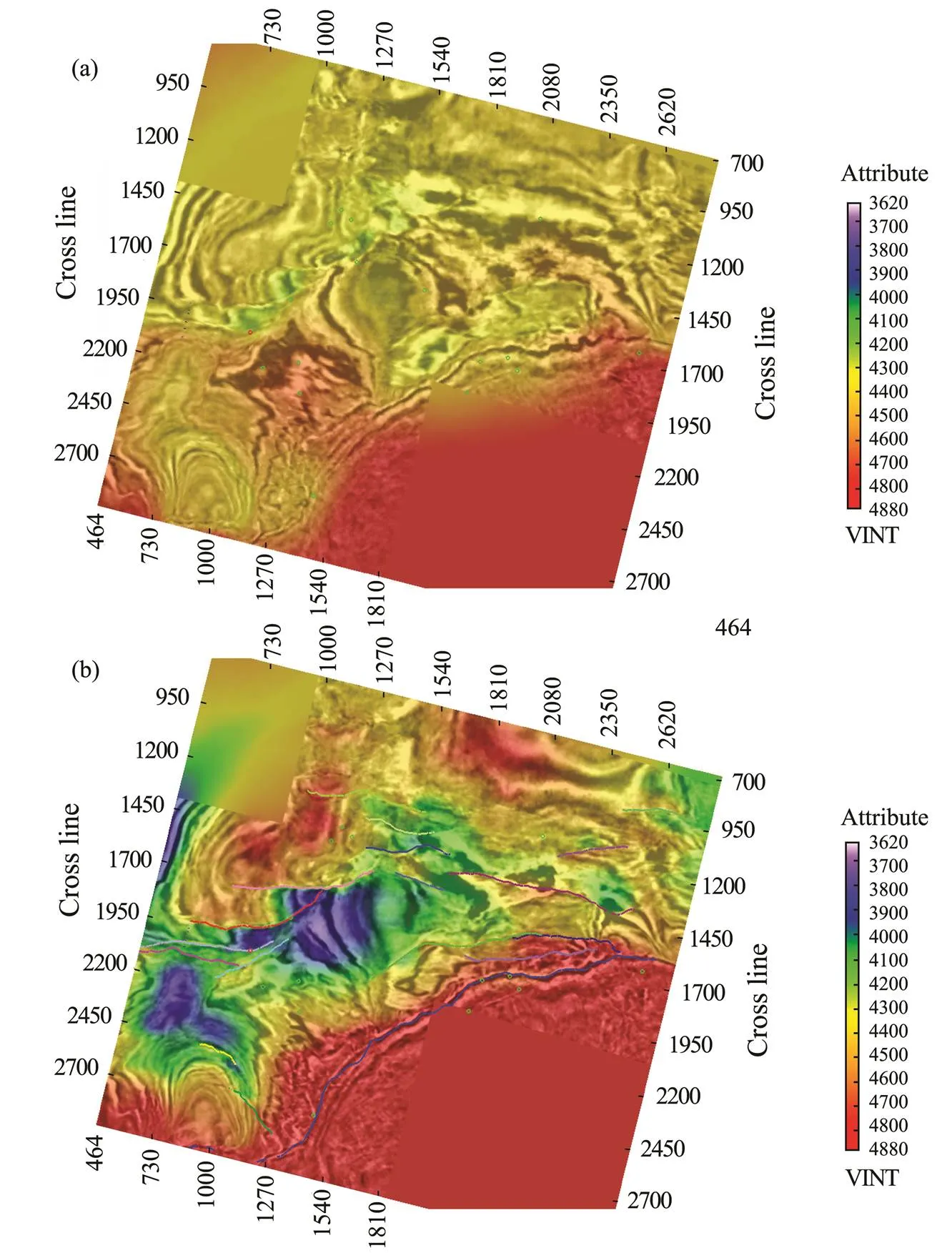
Fig.7 Slices of PSDM images overlaid on migration velocity. (a), conventional tomography; (b), fault-controlled constrained tomography.
Figs.8a and 8b show the PSDM results of conventional tomography and those of the proposed method in this paper, respectively. With respect to migration imaging using the proposed method, the reprocessing result for wavefield mi- gration is accurate, the imaging quality of the fault shadow zone in the fault zone is improved compared with that of the conventional method, and the contact relationship between the fault structure and formation is effectively improved. In addition, by using the high-precision velocity model, the imaging accuracy of the deep formation with respect to its structural configuration and continuity are also greatly improved. In the trap shape within the depth domain of the fault shadow area, the conventional results show obvious structural distortions in the fault shadow zone. In contrast, the reprocessing result effectively eliminates the illusions of the fault shadow structure, restores the true shape of the fault trap, and presents a depth domain trap within a reasonable structural configuration, which is consistent with the reservoir model and the development drilling height in this area (as shown in Fig.9). This provides a reliable reference for evaluations and research of the trap in the area.
The processing results show that the proposed method based on fault-controlled geological guidance-constrains can significantly improve the accuracy of velocity inversion and the imaging quality of the fault block area. The practicability of using this method is thus verified.
6 Conclusions
With the continuous development of hydrocarbon exploration, complex fault blocks and hidden hydrocarbon reservoirs are becoming targets. When processing the seis- mic data of complex fault blocks, it is key to obtain an accurate velocity inversion to obtain high quality seismic imaging. However, fault shadows in images are caused by dramatic velocity changes in complex fault blocks, and they are an important factor inhibiting structural identification, target evaluation, and subsequently hydrocarbon exploration and development. Based on the method of tomography velocity inversion of imaging gathers, this paper introduces an anisotropic Gauss regularization operator under the regularization principle, and then proposes a high-resolution tomography velocity inversion method based on fault-controlled geological guidance-constraints.
The model is applied to real seismic data, and the results show that it effectively improves the accuracy of velocity inversion and the rationality of the geological structure in a complex fault block area. In addition, the model is applied to a real hydrocarbon reservoir target area containing a complex fault block in the South China Sea, and the results show that it can solve the problem of fault block imaging in the target area and accurately determine the fault block traps. In this respect, the imaging quality of the fault block area is significantly improved that is helpfulfor subsequent seismic data interpretation and exploration.
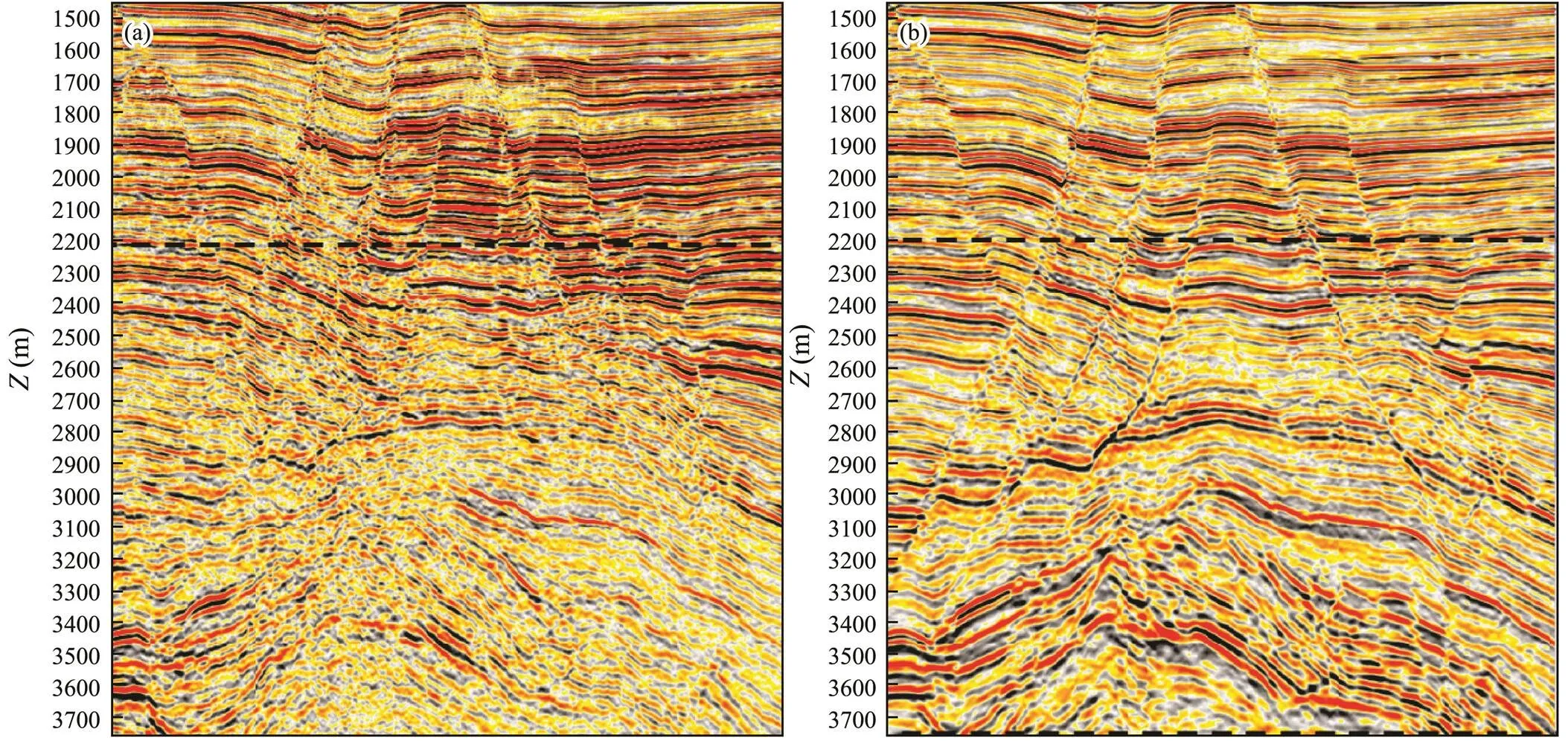
Fig.8 Comparison between imaging results in fault shadow area. (a), result of conventional method; (b), reprocessing result using proposed method.
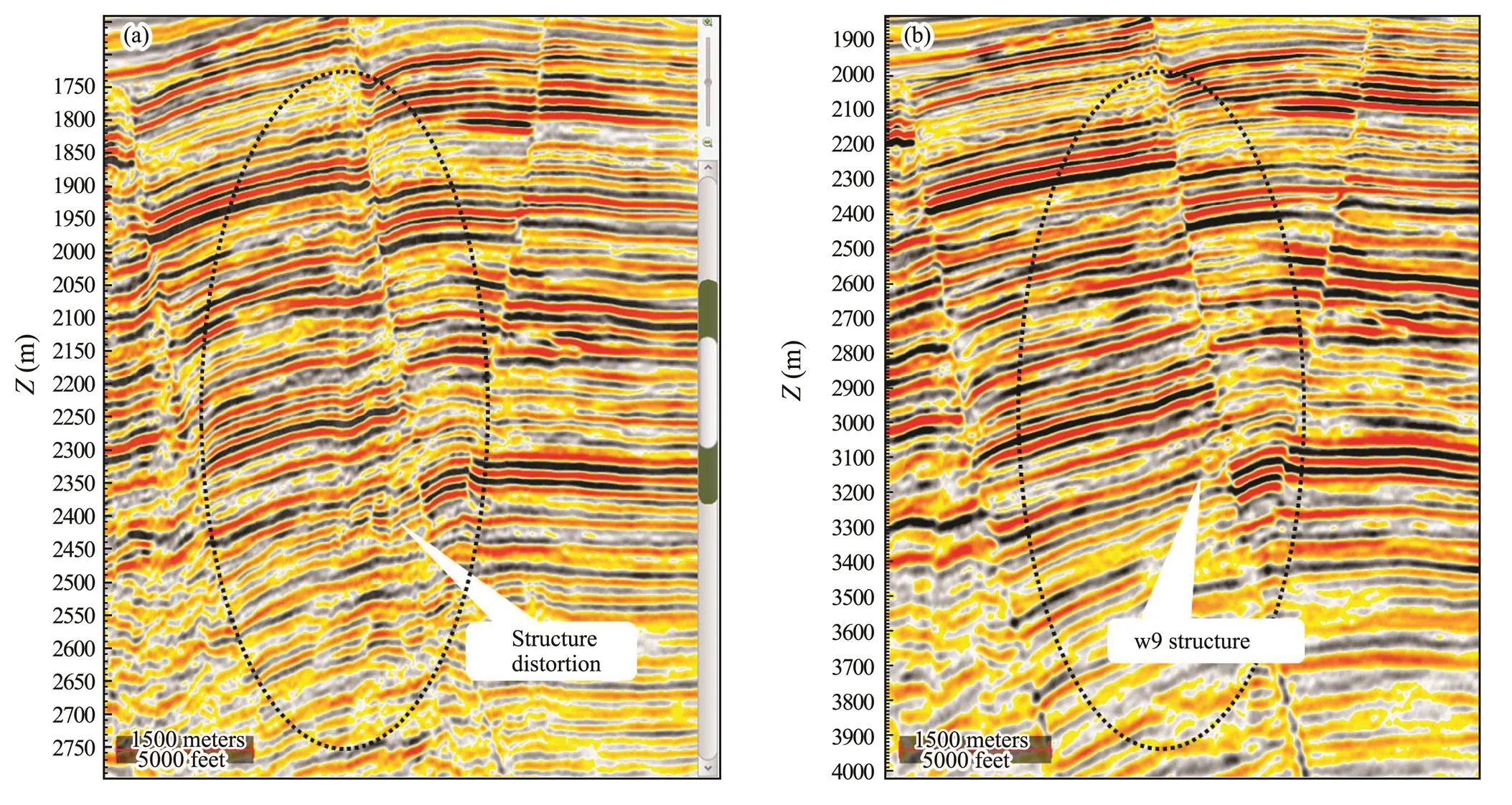
Fig.9 Comparison between representation of fault formation in fault shadow area. (a), result of conventional method; (b), reprocessing result of proposed method.
Acknowledgements
The authors are grateful for the support of the National Science and Technology Major Project of China (No. 20 16ZX05026-002), the National Natural Science Foundation of China (Nos. 42106072, 42074138), the Shandong Provincial Natural Science Foundation (No. ZR2020QD0 71), the Major Scientific and Technological Innovation Project of Shandong Province (No. 2019JZZY010803), the Fundamental Research Funds for the Central Universities (No. 201964016), the Shandong Province post-doctoral in- novation projects of special funds (No. 201903079) and the China Scholarship Council (No. 201906335010).
Appendix A: The Basic Theoretical Frame- work of Tomographic Inversion
The relationship between travel time and the velocity model can be expressed by the following integral equation,

whererepresents the function mapping between travel time and the velocity model;represents the slowness model;() represents the slowness value at, and the relationship of() with the velocity field can be expressed as()=−1();ds(,) represents the ray length of the-th ray aton the grid in the slowness model,, and() represents the path of the-th ray in the model,; andis the travel time of the-th ray. To ensure the linear form of the equation, the slowness value of the model is usually set as an unknown quantity, instead of the velocity value. Therefore, after introducing the medium slowness perturbation quantity, there is
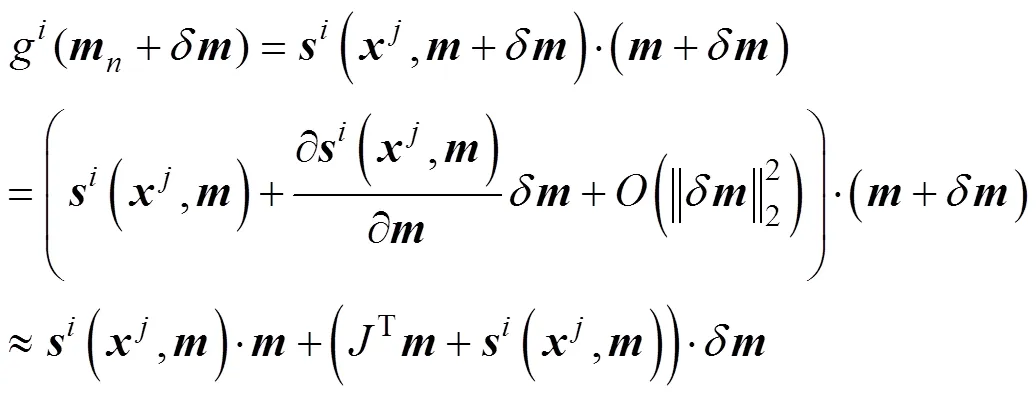
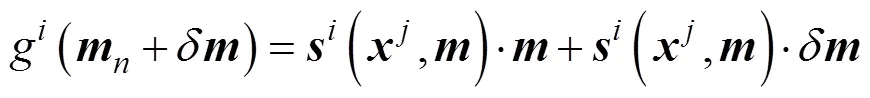
An approximate linear relationship between the slowness perturbation quantity and the travel time perturbation quantity can be further obtained as,
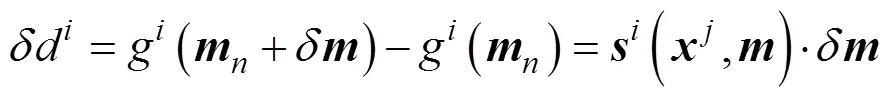
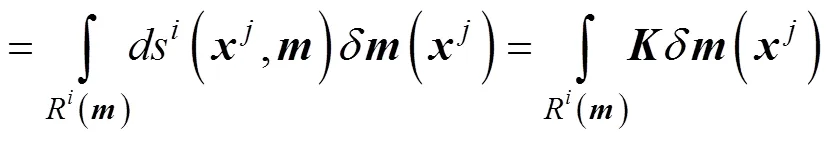
which is the Fredholm’s first type integral equation, where the matrix,, is the kernel function of the integral equation. It can be written in the following form,
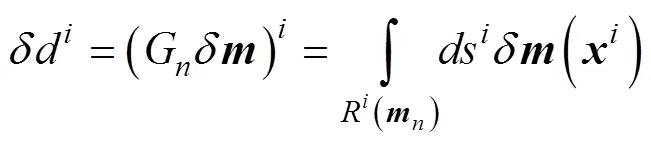
The above formula can also be written in the form of a matrix equation. The column vectors in the matrix can be regarded as the base function family of the expansion slow- ness perturbation function. The following Parsaval type re- lations exist in this coordinate system,

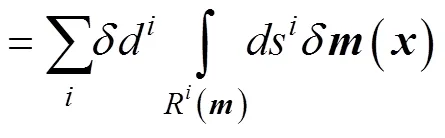
If the data space and the model space are adjoint, an adjoint operator (G)*exists, which projects the travel- time perturbation into a slowness perturbation. Therefore, the synthesis of (A-4), (A-5), and (A-6) derives the travel time inverse algorithm as follows,
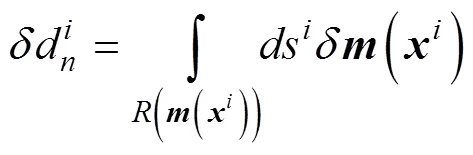

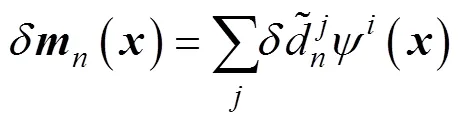
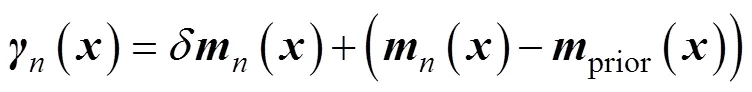
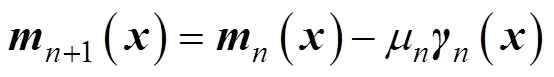
in which,

whereCrepresents the covariance matrix associated with the data, andCrepresents the covariance matrix associated with the model. Eqs. (A-7) to (A-12) define the basic linear relationship between travel time perturbation and slowness perturbation, which forms the basic velocity tomography inversion equation. Eq. (A-7) defines a large- scale sparse matrix equation, which can be solved using the ART/SIRT method (Gordon., 1971; Wu and Feng, 1993; Hosseini., 2012) or the LSQR method (Fan., 2016; Zeng., 2017), and a slowness perturbation estimate is then obtained. The information presented in this section shows the most basic theoretical framework of tomographic inversion.
Birdus, S., 2007. Removing fault shadow distortions by fault- constrained tomography.. San Antonio, 3039-3043.
Chapman, C. H., and Pratt, R. G., 1992. Traveltime tomography in anisotropic media–I. Theory.,109 (1): 1-19.
Cheng, G., Ma, Z. T., Geng, J. H., and Cao, J. Z., 2002. A review on the growth of seismic tomography., 25 (3): 6-12.
Clapp, R. G., Biondi, B. L., and Claerbout, J. F., 2004. Incorporating geologic information into reflection tomography., 69 (2): 533-546.
Fagin, S., 1996. The fault shadow problem: Its nature and elimination., 15 (9): 1005-1013.
Fan, J., Zhao, D., and Dong, D., 2016. Subduction of a buoyant plateau at the Manila Trench: Tomographic evidence and geodynamic implications., 17 (2): 571-586.
Gochioco, L. M., Novianti, I. R., and Pascual, R. V., 2002. Resolving fault shadow problems in Irian Jaya (Indonesia) using prestack depth migration., 21 (9): 911-920.
Gordon, R., Bender, R., and Herman, G., 1971. Algebraic Reconstruction Technique (ART) for three-dimensional electron microscopy and X-ray photography.,29 (3): 471-481.
Hart, M. J., Adewumi, O. A., Lang, C., and Rodriguez, G., 2015. High resolution velocity model building over the hoop fault complex.. New Orleans, 5189-5192.
Hosseini, N., Oraee, K., Shahriar, K., and Goshtasbi, K., 2012. Passive seismic velocity tomography on longwall mining panelbased on simultaneous iterative reconstructive technique (SIRT)., 19 (8): 2297-2306.
Liu, D. J., Huang, J. P., and Wang, Z. Y., 2020. Convolution-based multi-scale envelope inversion., 17 (2): 352-362.
Lu, M. H., Tang, J. H., Yang, H. Z., and Hu, B., 2005. P-wave traveltime analysis and thomsen parameters inversion in orthorhombic media., 48 (5): 1247- 1252.
Ohdachi, S., Yamamoto, S., Suzuki, Y., Purohit, S., and Iwama, N., 2019. Tomographic inversion technique using orthogonal basis patterns., 14: 3402087.
Qin, N., Li, Z., Yang, X., Zhou, Q., and Sang, Y., 2012. Image domain travel-time tomography velocity inversion based on automatic picking., 47 (3): 392- 398.
Rodriguez, G., Lundy, A., Hart, M., Lang, C., Cai, J., Chang, I.,., 2011. Imaging the hoop fault complexhorizon and fault constrained tomography.. San Antonio, 4025-4029.
Tarantola, A., 2004.. Society for Industrial and Applied Mathematics. Philadelphia, 81-96.
Trinchero, E., 2000. The fault shadow problem as an interpretation pitfall., 19 (2): 132-135.
Wang, Z. Y., Huang, J. P., Liu, D. J., Li, Z. C., Yong, P., and Yang, Z. J., 2019. 3D variable-grid full-waveform inversion on GPU., 16 (5): 1001-1014.
Woodward, M. J., Nichols, D., Zdraveva, O., Whitfield, P., and Johns, T., 2008. A decade of tomography., 73 (5): VE5-VE11.
Wu, J. P., and Feng, R., 1993. Nobody inversion using data segments in cross-hole electromagnetic tomography., 2 (3): 1-8.
Wu, Z., and Alkhalifah, T., 2015. Simultaneous inversion of the background velocity and the perturbation in full-waveform inversion., 73 (6): R317-R329.
Xu, S., Zhang, Y., and Huang, T., 2006. Enhanced tomography resolution by a fat ray technique.. New Orleans, 3354-3358.
Yang, S. Q., Wang, L. Y., Huang, J. H., and Zhang, J. Z., 2008. Velocity inversion from reflection travel-time and gradient of travel-time by tomography., 6 (1): 11-15.
Yang, W., 1997.. Geological Publishing House, Bejing, 45-79 (in Chinese).
Yao, G., and Wu, D., 2017. Reflection full waveform inversion.–, 60 (10): 1783-1794.
Yao, G., da Silva, N. V., and Wu, D., 2019. Reflection-waveform inversion regularized with structure-oriented smoothing shaping., 176 (12): 5315-5335.
Yao, G., Wu, D., and Wang, S. X., 2020. A review on reflection- waveform inversion., 17 (2): 334-351.
Zdraveva, O., Hydal, S., and Woodward, M., 2013. Tomography with geological constraints: An alternative solution for resolving of carbonates.. Houston, 4770-4774.
Zelt, C. A., and Smith, R. B., 1992. Seismic traveltime inversion for 2-D crustal velocity structure.,108 (1): 16-34.
Zeng, Q. C., Zeng, T. S., Ouyang, Y. L., Wang, X., Song, Y. Y., and Hu, X. H., 2017. A new tomographic inversion for static correction in complex mountain areas., 52 (3): 418-425.
Zhang, B., 2011. The study of tomography and velocity model building based on common imaging gathers. Master thesis. Tongji University.
Zhang, B., and Wang, H. Z., 2019. Velocity modeling for joint tomography of data domain first-arrival traveltime and imaging domain reflection traveltime.,62 (7): 2633-2644 (in Chinese with English abstract).
Zhang, R., Huang, J. P., Zhuang, S. B., and Li, Z. C., 2019. Target-oriented Gaussian beam migration using a modified ray tracing scheme., 16 (6): 1301-1319.
Zhdanov, M. S., 2002.. Elsevier Science B.V., Amsterdam, 61-64.
Zhou, C., 2013. Incorporating geologic information into reflection tomography with a dip oriented Gaussian filter., 70 (9): 2696-2712.
Zhou, C., Brandsberg-Dahl, S., and Jiao, J., 2009. A continuationapproach to regularize the reflection tomography with a 3D Gaussian filter..Amsterdam, cp-127-00381.
Zhou, W., Brossier, R., Operto, S., and Virieux, J., 2015. Full wave- form inversion of diving & reflected waves for velocity model building with impedance inversion based on scale separation., 202 (3): 1535-1554.
July 11, 2020;
August 26, 2020;
September 14, 2020
© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2021
. E-mail: zxb@sdust.edu.cn
(Edited by Chen Wenwen)
杂志排行
Journal of Ocean University of China的其它文章
- Meshless Method with Domain Decomposition for Submerged Porous Breakwaters in Waves
- Facial Features of an Air Gun Array Wavelet in the Time-Frequency Domain Based on Marine Vertical Cables
- Magma Evolution Processes in the Southern Okinawa Trough:Insights from Melt Inclusions
- Summery Intra-Tidal Variations of Suspended Sediment Transportation–Topographical Response and Dynamical Mechanism in the Aoshan Bay and Surrounding Area, Shandong Peninsula
- High-Resolution Geochemical Records in the Inner Shelf Mud Wedge of the East China Sea and Their Indication to the Holocene Monsoon Climatic Changes and Events
- Fast Quantification of the Mixture of Polycyclic Aromatic Hydrocarbons Using Surface-Enhanced Raman Spec-troscopy Combined with PLS-GA-BP Network
