数形结合思想在高中数学教学中融入论述

吴惠琴

(江苏省海门中学 226100)

在高中数学关于方程与不等式、函数、数列、集合、几何等多种问题中，数形结合思想都能够发挥出重要作用.因此，教师在课堂教学中，需要注意对学生数形结合、数形转化的思维培养，进而提高学生的解题综合能力.

本文先是对数形结合思想的含义进行了简要阐述，然后通过结合一些典型的数学问题，探究应该怎样恰当的融入数形结合思想.

一、数形结合思想的简述

事实上，数形结合的教学思想由来已久，只是在实践应用的过程中还存在不足之处.对于高中的数学知识内容本身来说，大致可以概括为是解决数和形问题，其中，如一般的数学符号、公式、数字表达等可以被称为“数”.而那些几何图形、函数图像等可以被称为“形”.二者是数量关系与空间图形的指代，两者的合二为一，可以使学生对知识内容的学习印象更深刻、理解更简便.在教学中将数形结合思想良好的教授或传递给学生，可以培养学生的数形转化思维与能力，进而帮助学生更容易找到解题思路并获得答案.

此外，与传统教学方法相比，采用数形结合思想开展教学，不仅可以让课堂变得更加富有生趣，而且还可以实现对学生学习动力的充分激发.这是因为学生一旦掌握了这种思想方法会发现，高中数学原来并没有想象的那么难，而且通过数与形的结合，还会发现其中的解题趣味.当然，由于一些学生感觉高中数学知识内容相对比较难，他们的注意力不容易集中，从而也会影响到教学质量.而当学生在探究数学问题的过程中，可以通过数与形之间的关联找到转化方法，并将抽象的数的问题进行具体的形的问题转化能力时，学生的解题思路便会越来越清晰.最终起到对学生学习积极性的调动以及解决数学问题能力的提高作用.因此，教师在课堂教学过程中所要做的，就是将数形结合思想有效的传递给学生.

总体来说，教师要努力培养学生的“以形助数”和“以数助形”的思辨能力.在解题过程中，懂得将数学语言转化为更为直观的图形语言，把抽象性的数学思维转化为直观的形象思维，最终实现数学综合能力的提升目标.

二、数形结合思想在高中数学教学中的融入

在高中数学知识内容的讲解过程中，教师应始终将数形结合思想进行讲解，从而起到助力理解能力提升、助力解题能力提升、助力数学思维建设的作用.

1.数形结合思想在集合问题中的融入

作为高中阶段的基础知识，集合问题一直都是各类数学问题的基础内容.所以，在高中初期，集合一直都是作为重点内容，需要学生进行扎实掌握的.因此，这就需要教师在教学过程中，更灵活的开展集合教学，从而使学生更容易理解和接受相关知识内容.数形结合思想在高中数学集合问题中的应用，主要表现就是数轴法和维恩图法.这种方法比较适用于那些给出的数量关系相对比较复杂，题干线索不容易找出的数学问题.良好的运用维恩图法往往能够达到事半功倍的教学效果.如下图所示：

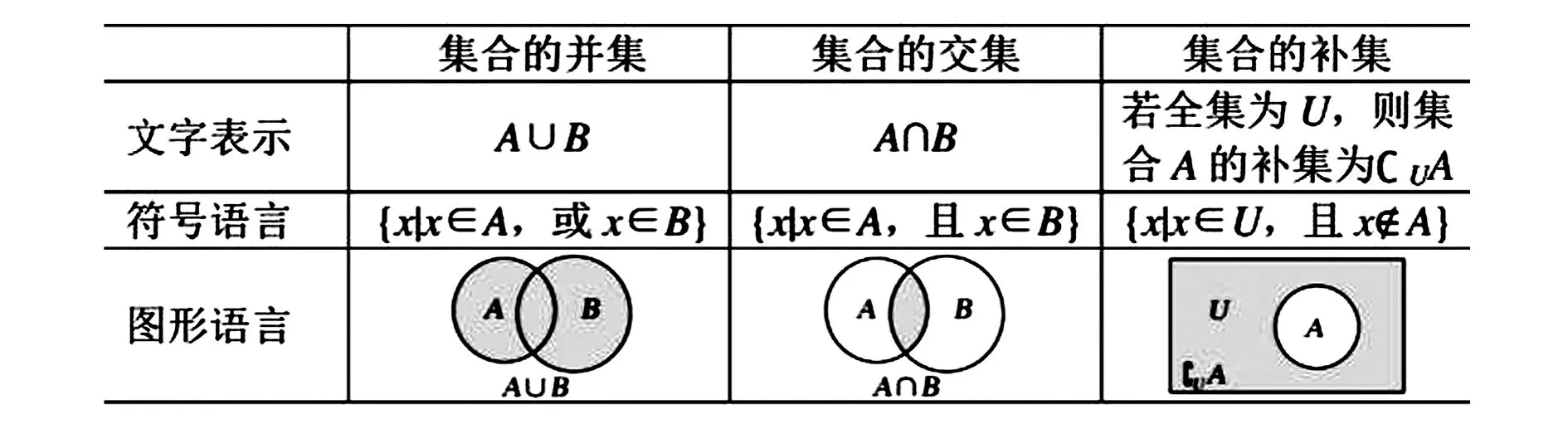
图1

2.数形结合思想在函数问题中的融入

在数形结合思想的融入过程中，函数问题是良好的教学载体.在教学过程中，教师除了教授学生对一些比较常见的函数图像进行熟练掌握外，还需要将函数与方程、以及曲线之间的差别和统一等知识内容教授给学生，从而提高学生发现条件中的几何意义的能力，进而顺利的将相对应的几何图形刻画出来.此外，学生在学习的过程中，还要参照图形的性质，能够将数学式的几何意义分析出来.只有这样，学生才能充分的发挥出数形结合思想的作用，从而实现个人解题能力的全面提升.如在一些函数不等式问题中，由于运用代数的方法进行解题存在步骤和过程比较繁琐的情况，且不利于学生的思维锻炼与形成.为此，教师还是需要引导学生运用数形结合的思想进行解题，懂得将代数问题转化为几何问题的思想方法的运用，从而实现对问题的化简目标，最终达到提高解题效率的效果.

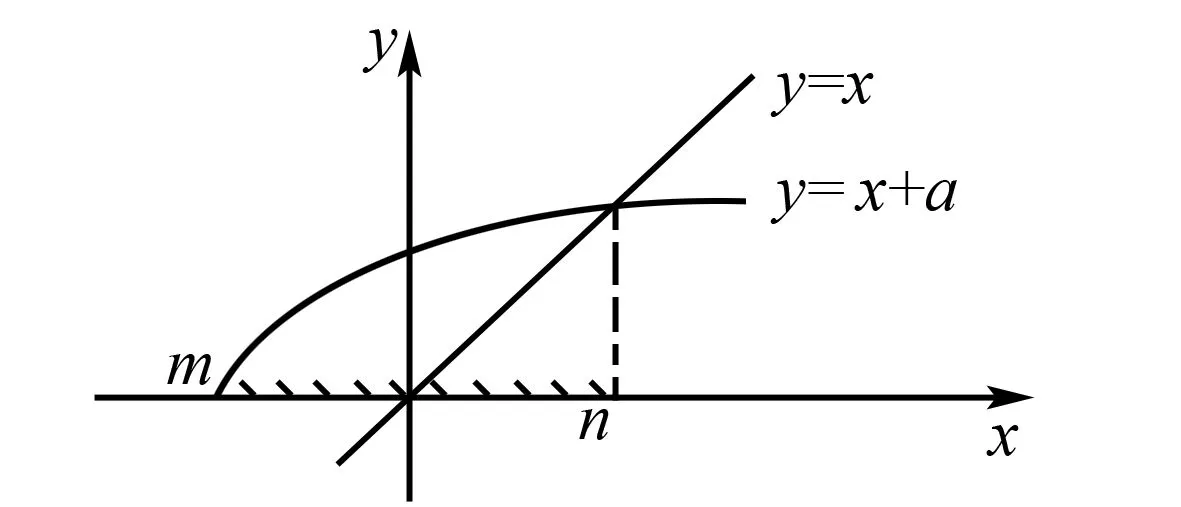
图2

此外，在函数零点的问题教学中，以及方程的根等问题教学中，教师需通过数形结合思想的导入，让学生了解它们与函数图像交点的密切联系.例如：函数f(x)=|x-2|-lnx的定义域内的零点个数是几？根据问题可以知道这一函数的定义域是(0,+∞)，在同一直角坐标系中，可以进行函数图像绘制，即y1=|x-2|(x〉0),y2=lnx(x>0)，详见下图.然后，引导并组织学生进行图像观察，从而观察得到最终答案是2.

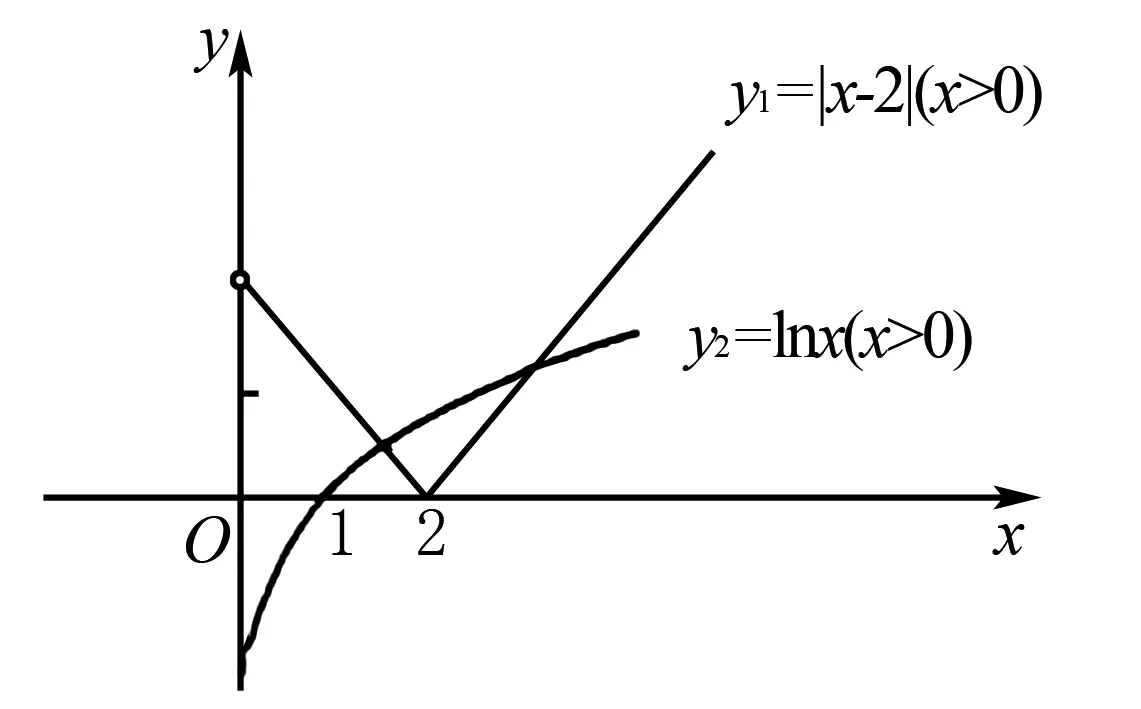
图3

3.数形结合思想在几何问题中的融入

在几何问题中，包含平面解析几何、立体解析集合，前者属于二维空间上的解析几何问题、后者属于三维空间上的解析几何问题，后者要比前者更为复杂而抽象.而在众多几何问题的解答过程中，良好的应用数形结合思想，可以将题干或条件中的数和形进行一一对应，进而将数量关系通过图形、位置关系更加直接的表现出来，从而达到以形助数、或以数解形的效果.因此，当遇到几何问题时，教师最重要的是要教授学生将条件和问题之间的数量，以及二者的位置关系加以厘清，彻底的弄清楚数和形之间的对应关系.当学生通过长期的训练，对数形结合方法有了熟练的掌握后，便能够做到举一反三，融会贯通了.为此，一方面，学生要理清以几何条件、元素为基础，而构建的各种概念，如复数、三角函数等；另一方面，学生要对自己所面对的题目中，理清等式结构，或代数方程式结构，以及其中所包含的比较明显的几何意义；再一方面，还要理清图像和函数之间的对应关系；最后一方面，学生要对曲线和方程之间的对应关系进行理清等.

这种通过数形结合来解决问题的过程，能够快速而准确的找到解题思路并获得正确答案.

总而言之，数形结合思想在教学过程中的合理融入，对学生数学思维的形成，以及数学问题的解题能力的提升，都具有重要的促进作用.通过图形的融入，可以让学生对各类题目的理解更加深刻而清晰，不仅能够彻底的提高其解题的速度与准度，更能够锻炼其数学思维能力，从而让学生懂得运用转化思维、逆向思维进行数学知识的学习.