基于ANSYS Workbench新型折叠翼无人机机翼仿真优化分析
2021-12-22左晓军齐元胜马克西姆
左晓军,齐元胜,马克西姆
(北京印刷学院 机电工程学院智能制造实验室,北京 102600)
1 引言
本文主要是对新型折叠翼无人机的机翼进行有限元分析。首先建立了该新型折叠翼无人机机翼的三维模型,并将其模型导入到 ANSYS Workbench 中,分别对该机翼做了静力分析和模态分析。根据无人机的起飞重量、安全系数及过载系数计算无人机飞行过程中需要提供的升力,简化机翼受力模型,进行静力学仿真,然后对比无人机机翼理论能够提供的升力,对折叠翼无人机的机翼进行优化。无人机在飞行过程中机翼可以简化为悬臂梁,机翼会发生振颤现象,所以需要对机翼做模态分析,研究其振动特性。为无人机机翼设计优化提供一些经验。
2 无人机机翼的总体设计
该无人机的初级设计要求是起飞质量7 kg,动力来源是太阳能,要求具有重量小、续航长和结构强度高等特点。根据无人机的起飞重量,通过简单的翼载荷、推重比、飞行速度和起飞距离等计算得出无人机的设计参数。这里重点做机翼的有限元分析,所以这里直接给出设计结果,见表1。
表1 无人机设计参数
?
该无人机要求机翼有大展弦比(翼展和翼弦的比值称为展弦比)。无人机的起飞质量达7 kg,所以对机翼的设计要求较高,需要有高效的气动布局。选择 NACA4412翼型,NACA4412 翼型具有良好的几何特性和气动特性,是一个非常成熟的翼型,某大学用 NACA 翼族设计了太阳能无人机。为了设计制造方便,同时具有良好的气动特性,该无人机采用矩形翼,通过在翼型库 ProfiliV2 中对比分析该翼型的升阻比、升力系数、阻力系数和极曲线等参数,确定该翼型可以满足设计要求。
机翼需要承受的力较大,需要保证有足够的强度,故机翼做成盒式结构,主要的受力部件是机翼的主梁,其他的翼肋架在主梁上支撑成盒式结构,维持机翼剖面所需的气动外形。另外还有副梁、前缘和后缘等共同构成机翼的盒式结构,使其具有更强的抗扭转能力。机翼模型如图1所示。

图 1 机翼模型
3 机翼静力分析
3.1 机翼受力分析
新型折叠翼无人机,机翼垂直于机身,安装在机身两侧,如图2所示。机翼是为无人机提供升力的装置。机翼静力分析的关键是抽象力学模型,机翼与机身通过铰链和销钉连接,为固定连接,机翼的另一端没有支撑点,处于悬空状态,所以将机翼抽象为悬臂梁。
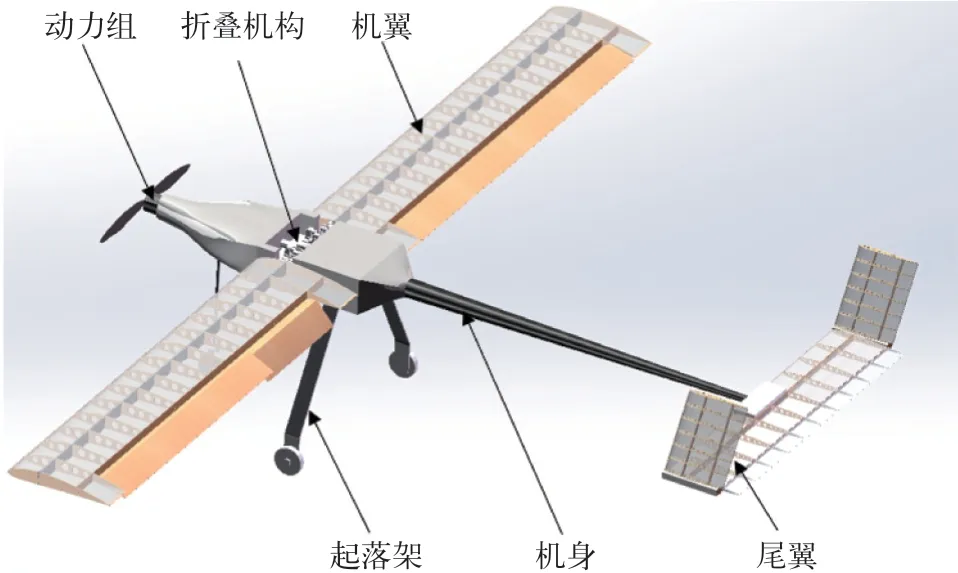
图 2 机翼与机身连接状态图
无人机实际在空中飞行时,受力非常复杂,忽略机翼的内力影响,其主要外载荷有集中力、机翼重力和分布气动力,该机翼为矩形翼,翼型的横截面是矩形,所以截面气动载荷基本相同。在设计时,已经规定无人机的起飞质量为7kg,根据设计参数及查阅相关资料得知,该无人机的过载系数n
= 3.0,安全系数f
= 1.5。则每一侧机翼需要的升力F
′为
F
为无人机机翼的总重力,G
为无人机的起飞重量;n
为过载系数,f
为安全系数。当起飞质量为 7 kg 时,经查阅资料可知,n
= 3.0,f
= 1.5,代入式(1)中可得F
′= 158N。我还想留她多呆会儿,她说,不行,四点钟,要准时给客户送货。付玉说走就走,还没等我穿上衣服送她。她已经开门走了,整个楼道里,留下了一股淡淡的芙蓉花的香味。
根据伯努利定律可知,无人机机翼上下面的压力差即为无人机的升力。机翼的升力公式为

L
是机翼升力,C
是机翼升力系数,ρ
是空气密度,S
是翼面积,v
是无人机的巡航速度。该翼型的升力系数和升阻比曲线如图3所示。将图3中两幅图结合来看,由图3b升阻比曲线找到该翼型升阻比最高时迎角为6°,在迎角为6°时机翼的升力系数为1.1,空气密度在标准状态下为1.297 kg/m。机翼的弦长为0.3m,翼展为 3m,所以单侧翼面积S
= 0.42 m,巡航速度v
=120 km/h = 33.3 m/s。将数据代入式(2)得该机翼可以提供的升力L
= 356N。与无人机单侧机翼需要的升力相比,该机翼可以提供足够的升力来维持无人机的航行。3.2 添加材料
根据无人机的设计要求,选择碳纤维作为该无人机机翼的材料。碳纤维是一种高刚度、高抗拉强度、低重量、高耐化学性、耐高温和低热膨胀的优异材料,被大量应用在航天领域。选择 ANSYS Workbench 中材料库中碳纤维(395GPa)材料,材料的性能参数见表2。
表 2 碳纤维材料性能参数
?
3.3 网格划分
网格划分对有限元分析的结果起着至关重要的作用。对于三维几何体主要有自动划分法、四面体划分法、六面体划分法、扫掠划分法和多区域划分法。四面体网格可以施加在任何物体上,且在关键区域容易使用曲度和近视尺寸功能细化网格。对形状不规则的翼肋在其边缘处需要做细化处理,采用四面体网格划分。在一些重要的位置,还可以对网格进行尺寸控制,进一步细化网格。最后对生成的网格进行质量检测。生成的网格如图4所示。
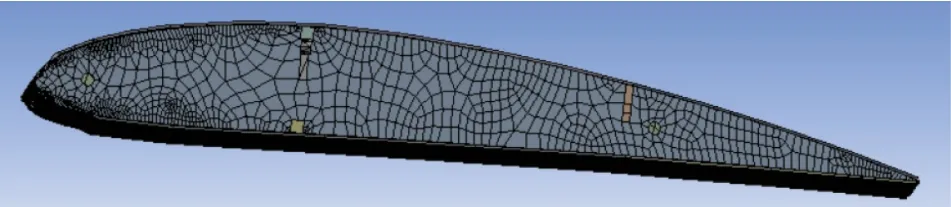
图 4 机翼有限元网格
3.4 仿真结果
通过上面的分析可知,该机翼可以看做是固定端约束,即机翼的一端添加固定端约束,然后在机翼的下表面施加均布载荷,载荷大小为158 N,通过仿真计算,得到机翼总变形如图5所示和机翼等效应力如图6所示。

图5 机翼总变形图

图6 机翼等效应力图
根据仿真分析云图,机翼结构最大变形量为 17 mm,最大等效应力为 1.5×10Pa,通过仿真分析可知,该机翼的受力变形在线弹性范围内。但是从变形图中可以明显的看出,在机翼的另一端的后梁处发生变形比主梁处明显,造成这一现象的原因可能是机翼后梁处受力较大,但是在实际飞行中,主要受力位置在主梁处,后梁的变形应该会有相应的减小。
3.5 优化设计
根据最大应力准则,在158 N载荷作用下,机翼的机构可以满足强度要求。查阅相关资料,机翼的最大挠度不得超过翼展的2.5%。通过机翼变形图,计算此时该机翼的最大挠度所占翼展的百分比仅为0.6%,远远低于2.5%,材料的裕度较大。无人机的设计任务要求是起飞质量7 kg的新型折叠无人机,在能完成设计任务的前提下,应该尽量把无人机做小一些,这样方便无人机的运输、存储等。因此对该新型折叠翼无人机的机翼做了进一步的优化设计。
根据机翼的升力公式

该无人机在规定起飞质量的前提下需要的升力为158 N,根据式(3),推导得到该无人机的翼面积公式为

无人机原机翼模型的展弦比为10,机翼矩形翼,则该机翼的弦长公式在近似后可以表示为

则整理公式(3)(4)(5)后得无人机的弦长公式为
翼展公式为
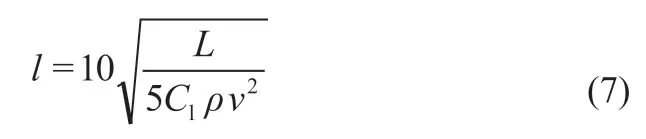
代入以上数据计算得到优化后机翼的弦长为 210 mm,翼展为 2 100 mm。针对计算得到的优化后的结构,对机翼进行建模。机翼模型如图7所示。

图 7 优化后机翼模型
对优化后的机翼模型做有限元分析,同样,将其简化为悬臂梁模型,一端为固定端约束,然后施加158 N的均布载荷,得到机翼总变形如图8所示和机翼等效应力如图9所示。
从优化后机翼总变形图上可以看出该机翼的最大变形量为23 mm,最大等效应力为3.1×10Pa,与优化前相比最大形变量增加了6 mm,最大等效应力变为原来的两倍。但是优化后机翼的最大挠度所占翼展的百分比变为1.1%,远小于2.5%,此时该机翼仍然符合设计要求。根据仿真结果,优化后的机翼更适合实际加工生产。

图 8 优化后机翼总变形图

图 9 机翼等效应力图

4 机翼模态分析
模态分析是分析机械结构固有频率、阻尼特性等动力学参数的重要方法,按照某一固定频率振动的过程中,系统结构中各质点偏离原来位置的情况。通过固有频率、阻尼比和模态振型等特征量来反应结构动力特性。为结构系统的振型特征分许、振动故障诊断和预报以及机构动力特性的优化设计提供依据。通过模态分析,可以求解出机翼在各个阶次的应变情况,对机翼的稳定性进行进一步的分析,从而对机翼设计改进提出修改意见。
机翼的有限元模型已经在 SolidWorks 软件中绘制好,在保存时,需要将其保存为x_t格式的文件,然后导入到ANSYS Workbench 中,导入后的模型如图10所示。
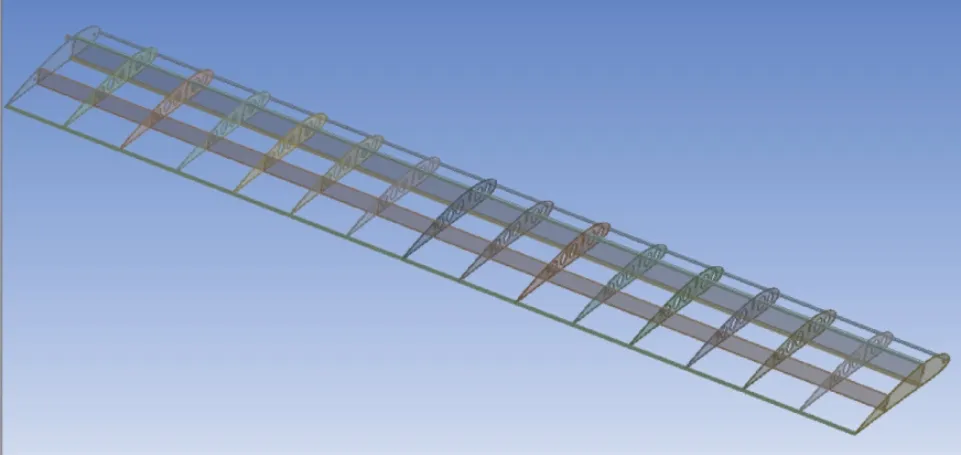
图 10 机翼模型
无人机在实际飞行的过程中,机翼固定连接在机身上。以右机翼为例,添加机翼的左端为固定端约束,如图11所示。
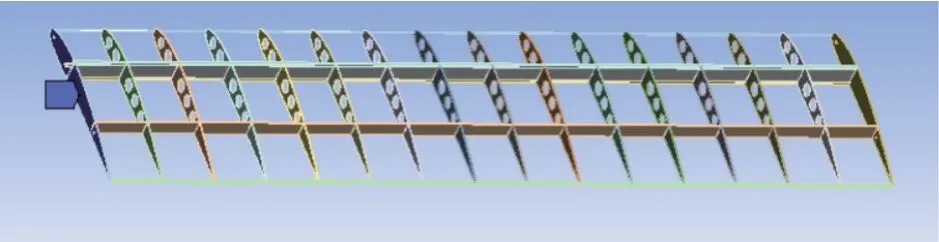
图 11 添加固定端约束
在基础设置完成后,求取该机翼模型的前二十阶模态,这里仅取前十阶模态的振型,如图12所示,模型固有频率见表3。
随着模态阶数的增加,固有频率逐渐增加,在前4阶模态中,固有频率随模态的增加基本比较缓慢,在5到6阶模态中,固有频率的数值相对较大。低阶振型模型对研究无人机机翼起着决定性的作用。前四阶主要表现为扭转振动,后几阶则主要表现为弯曲振动,扭转振动的频率较低,扭转变形主要施加到翼肋上,对于扭转变形,需要加强翼肋的强度,避免翼型出现变形。从第五阶开始,主要振动变为弯曲振动,弯曲振动主要施加在机翼的主梁和后梁以及前后缘上,所以对弯曲振动可以加强主梁、后梁等结构强度,避免发生过大的弯曲。对于其他高阶模态振型图,在实际中可能出现的概率非常小,如果对高阶模态下的复杂变形有特殊设计要求,则需要对机翼进行更近一步的优化设计。飞机飞行时刻,受到的载荷多种多样,所产生的变形也多种多样,在设计时应充分考虑机翼的基本属性,避免在特殊模态下飞行,如果无法避免,应对机翼结构进行加强或者优化。

图 12 前十阶模态振型图(顺序从左到右依次排列)
表 3 碳纤维材料性能参数
?
5 结束语
无人机是一个复杂的系统,机翼是无人机最重要的部分之一。静力学仿真是对机翼刚度强度等物理量的检查。模态分析是为了对机翼结构的稳定性进行分析。
在静力分析的过程中,发现该机翼的设计安全裕度较大,为了方便无人机的运输、存储等,减小了无人机的体积,对其机翼进行优化。在展弦比不变的情形下,通过对机翼升力公式的变形推导,得到优化后无人机的尺寸。优化后机翼的最大挠度与翼展的比值由原来的0.6%变为了1.1%,均小于2.5%的临界值。优化后机翼更为合理。不同的振动频率下,机翼的模态不同,变形的种类不同,变形大小不同。实际设计翼型时需要考虑飞行环境中气动弹性的频率,避免机翼发生过大的变形影响飞行安全。在机翼优化后,无人机的其他部分都需要做相应的优化改进,本文只做了机翼的优化部分,其他部分的优化设计可参考机翼优化方案。
