不平衡量对非线性转子-挤压油膜阻尼器系统临界转速影响的研究

陈文超，刘 超，方 翔，王聚存，黄晓鸣，陈超群

（1.上海衡望智能科技有限公司，上海 201600；2.中国航发南方工业有限公司，湖南株洲 412000）

0 引言

在航空发动机动力涡轮转子朝着超细长，超高速的发展的趋势下[1]，转子的工作转速一般处于超临界状态，有的甚至超过二阶、三阶临界转速。由于转子本身的不平衡量势必会带来转子在升速过程中过临界转速时振动及挠曲变形较大的情形，为了保证动力涡轮转子可以安全平稳运行，动力涡轮转子在装机前要先经过严格的动平衡[2]。对于这种柔性细长轴超临界转子，在选取合适的转速进行动平衡时，需要知道转子运行的模态信息如临界转速等[3]。这种航空发动机涡轮转子一般会采用弹性支撑加挤压油膜阻尼器的结构来抑制转子的振动。

关于挤压油膜阻尼器的研究论文虽然很多，但大多集中于研究挤压油膜阻尼器的设计，如Vance[4]指出，在实际条件允许的情况下，支承刚度应设计的尽量小。因为减小支承刚度可有效减小转子通过临界转速时的振动峰值与支承外传力。也有很多学者研究了挤压油膜阻尼器的非线性问题，如双稳态现象。很少有论文研究由于挤压油膜阻尼器的存在，转子-挤压油膜阻尼器系统的临界转速是会随着不平衡量的大小而变化的，进而影响动平衡所需的模态信息和影响系数。本文采用ANSYS 有限元分析软件对动力涡轮转子-挤压油膜阻尼器系统进行动力学建模及临界转速计算，为涡轮转子的高精度动平衡提供理论依据[5]。

1 涡轮转子-挤压油膜阻尼器系统的有限元计算模型

1.1 涡轮转子系统的有限元模型

本文所研究的动力涡轮转子系统如图1 所示，包括输出轴、短轴、模拟涡轮盘（以及四个轴承支撑，其中一号轴承和三号轴承为滚动轴承直接支撑，二号轴承和四号轴承处有弹性支撑且有挤压油膜阻尼器。

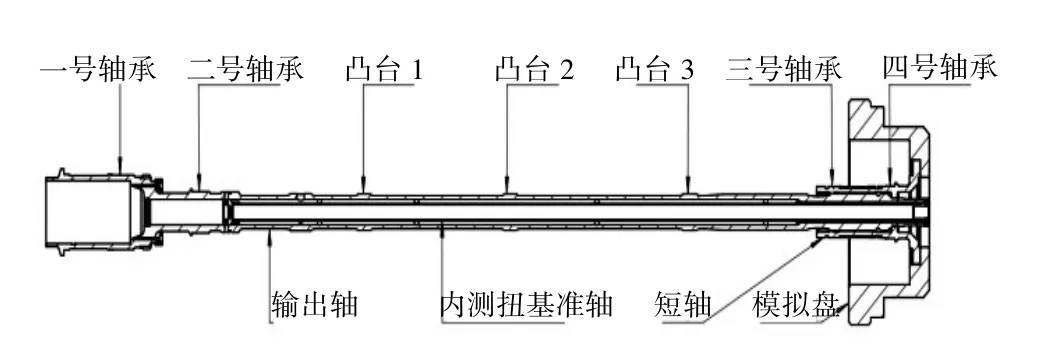
图1 动力涡轮转子结构布局图

使用有限元分析软件ANSYS 对转子单元体部件进行有限元建模。本文中，输出轴、短轴和模拟涡轮盘都选用梁单元BEAM188 来建模，一些随转子旋转的小零件直接附加在轴上成为整体，输出轴与短轴采用花键结构联接，内外花键都简化为圆环，用2个COMBI214 单元连接在一起，同时忽略一些细小的局部结构（如倒角，小孔等）。模拟涡轮盘是通过过盈与短轴装配在一起的，因此这二者通过若干个节点耦合直接连在一起。

动力涡轮转子单元体三维模型如图2 所示。

图2 ANSYS 仿真模型

一至四号支撑都采用COMBI214 单元来建模，其中，1 号和3 号轴承为滚动轴承，近似为刚性支撑，支撑刚度设置为2×108N/mm，因为刚度足够大，阻尼可以忽略不计。一号和四号轴承为弹性阻尼支撑，即滚动轴承通过油膜由鼠笼支撑，这里实际上有3个支撑，滚动轴承、挤压油膜阻尼器以及鼠笼，挤压油膜阻尼器与鼠笼为并联关系，滚动轴承与挤压油膜阻尼器和鼠笼为串联关系，设滚动轴承的刚度k1=2×108N/mm，阻尼忽略不计，鼠笼的刚度k2=0.3×107N/mm，阻尼为零，挤压油膜阻尼器的刚度和阻尼系数分别为k0和C0，则可以根据它们的串并联关系计算出总的刚度、阻尼系数：

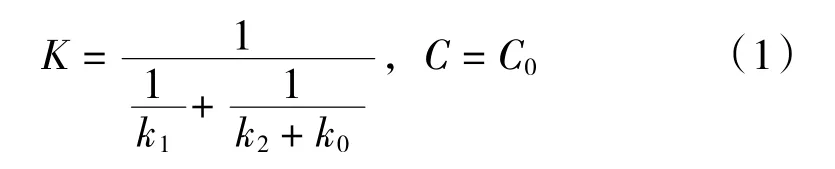
其中，因为k1远大于k2和k0，由上式知，k1基本可以忽略不计。

1.2 挤压油膜阻尼器刚度和阻尼系数与偏心率的关系分析

二号及四号轴承处有弹性支撑及挤压油膜阻尼器，由上面的分析可知，弹性支撑的结构阻尼非常小，与挤压油膜阻尼器相比可以忽略不计，所以二号及四号轴承处的阻尼主要取决于挤压油膜阻尼器阻尼，二号及四号轴承处的刚度则为鼠笼刚度和挤压油膜阻尼器刚度之和[6]。挤压油膜阻尼器的刚度和阻尼计算方法[7]如下：

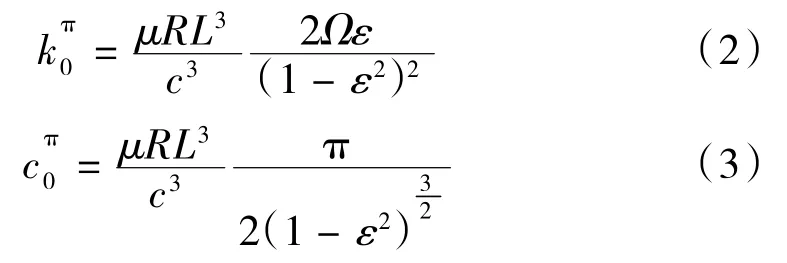
其中：μ为润滑油的动力粘度；R为挤压油膜阻尼器的平均半径；L为阻尼器油膜长度；c为挤压油膜阻尼器的半径间隙；Ω为挤压油膜轴颈进动角速度；ε为偏心率；式中的上标π 表示采用半油膜假设。

当阻尼器结构确定后，上面公式中的左边部分为常数，根据阻尼器的结构参数设：

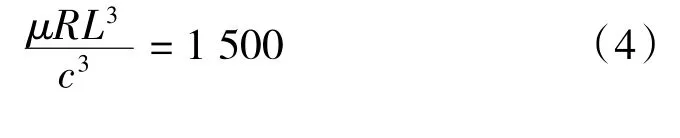
则可以计算得到不同转速、不同偏心率下阻尼器的刚度和阻尼系数，如表1、表2 所示，由表中可以看出，挤压油膜阻尼器的刚度和阻尼系数随着转速和偏心率的变化而变化，刚度系数的变化可达1 个数量级以上，阻尼系数也会出现成倍的变化。因此在计算临界转速和不平衡响应时，如果采用固定的刚度阻尼系数，则计算结果与实际情况会有较大的出入。

表1 偏心率ε=0.1 时的挤压油膜阻尼器刚度和阻尼系数

表2 偏心率ε=0.6 时的挤压油膜阻尼器刚度和阻尼系数

1.3 非线性谐响应计算方法

由于挤压油膜阻尼器的刚度阻尼系数与轴颈的振幅相关，因此无法用计算坎贝尔图的方法计算转子系统的临界转速。本文采用稳态谐响应的方法，通过识别谐响应的峰值以及相位的变化情况，得到临界转速。

在计算稳态不平衡谐响应时，采用变刚度阻尼系数。具体方法如下：选用ANSYS 求解器中的谐响应分析进行稳态不平衡响应计算，即选择分析类型为harmic。计算中考虑陀螺力矩的影响，设置Coriolis为ON。在转子的某些位置施加不平衡力，同时通过“synchro，，rotor1!”命令实现不平衡力与转速的同步。采用转速循环的方式在ANSYS 中进行分步谐响应计算，给定转速步长以及计算的起止转速，则每一步计算的角速度Ω都是已知的。一般情况下第一步的角速度很低，转子振幅很小，因此不失一般性，可以假设偏心率ε=0.01，将第一步的Ω和ε代入公式（2）和公式（3），分别计算二号轴承和四号轴承的挤压油膜阻尼器刚度系数k0和阻尼系数c0，再根据鼠笼的刚度k0计算出二号轴承和四号轴承的总刚度和总阻尼系数，然后用Rmodif 指令修改二号轴承和四号轴承的支撑刚度和阻尼系数。接着完成当前转速步的谐响应计算，并提取二号轴承和四号轴承的轴颈位移值作为挤压油膜阻尼器的下一转速步的偏心距，分别计算2 个阻尼器的偏心率。转速增加一个步长，然后重复前面的步骤计算各个转速下的谐响应，直至终止转速步。当转速步长取足够小时，这个算法已经足够保证计算精度。

2 不同不平衡量下转子系统谐响应计算结果及其分析

2.1 不平衡量对临界转速的影响

本文模型所研究细长轴转子工作转速在21 000 r/min，要经过转子的前两阶临界转速。在模型中凸台2 处施加不平衡量，为不平衡量质量，为不平衡质量偏心半径，转速步长180 r/min，采用上述的非线性谐响应计算方法，计算得到在不平衡量为5 gmm、10 gmm、15 gmm 情况下二号及四号轴承处弹性支撑轴径振幅的变化及凸台2 处的挠度响应，分别见图3、图4 和图5 所示，由于篇幅关系，本文没有给出对应的相位图。

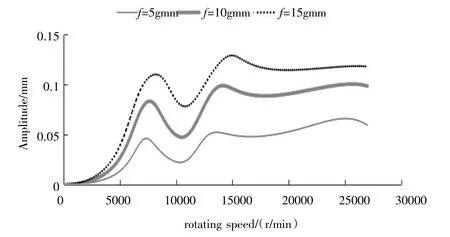
图3 凸台2 处施加不平衡量的情况下二号轴承处弹性支撑轴颈振幅

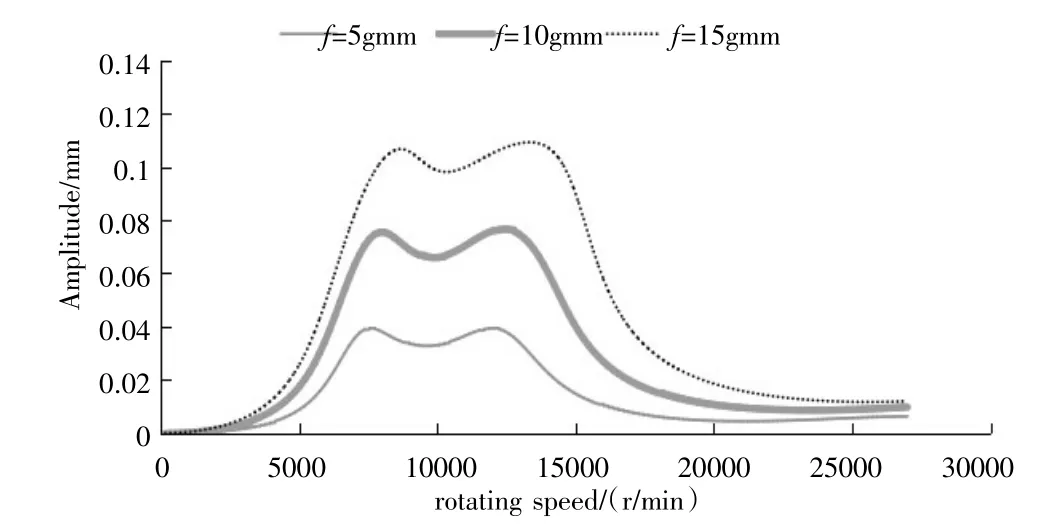
图4 凸台2 处施加不平衡量的情况下四号轴承处弹性支撑轴颈振幅

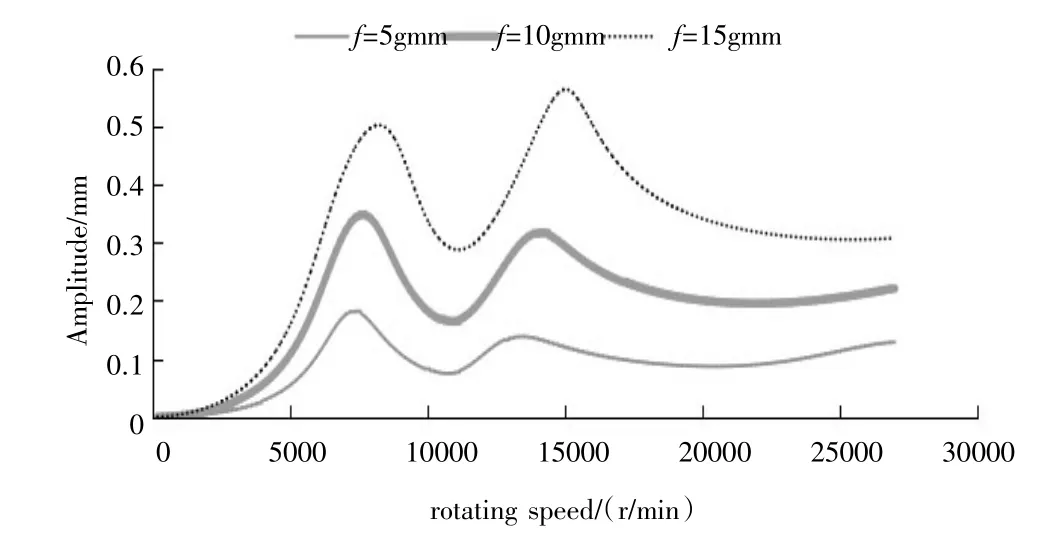
图5 凸台2 处施加不平衡量的情况下凸台2 处的挠度

从图3 和图4 可以看出，随着施加的不平衡量的增加，二号轴承和四号轴承处弹性支撑轴径振幅也会增大，弹性油膜阻尼器的偏心率随之变大，油膜刚度便会随之增大。从图3 或图5 可以得到谐响应峰值所在的位置（图3 至图5 中峰值位置都是一致的），即为转子系统的一阶和二阶临界转速，结果列于表3 中。由表3 可知，随着转子凸台2 处不平衡量从5 gmm 增加到15 gmm，转子的一阶临界转速从7 380 r/min 提高到8 100 r/min，转子的二阶临界转速从13 500 r/min 提高到14 940 r/min。由此可见，转子不平衡量的增加会显著影响到转子的临界转速。

表3 凸台2 处施加不同不平衡量下转子的临界转速

从图4 至图6 中还可以看出：虽然不平衡量从5 gmm 线性增加到15 gmm，但是在一阶和二阶临界转速附近很宽的范围内，谐响应幅值并不是线性增加，这是因为在不同的不平衡量作用下，转子的临界转速明显改变了，而在临界转速附近，转子的振幅和相位会有急剧的变化，由此也导致了动平衡影响系数的变化，这将在下一小节进一步探讨。

2.2 不平衡量对动平衡影响系数的影响

在上述3 组不平衡量的基础上，分别在凸台2处施加2∠0 gmm 的试重，通过同样的谐响应计算得到三个凸台处的位移向量，并分别计算这3 处的动平衡影响系数，得到的计算结果如表4 和表5 所示，不失一般性，表中仅给出了5 gmm 和15 gmm 两种条件下的影响系数。

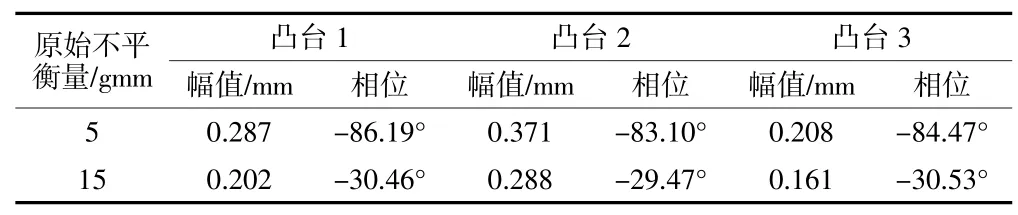
表4 不同原始不平衡量下的动平衡影响系数（转速为7560r/min）

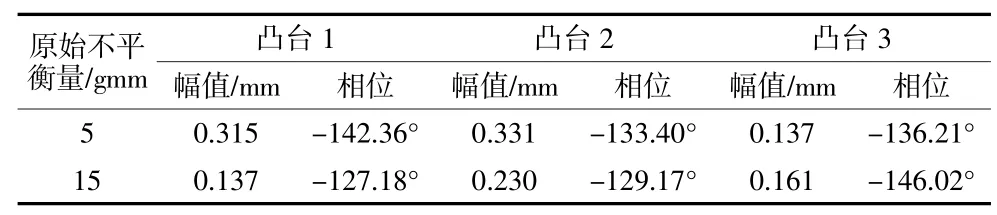
表5 不同原始不平衡量下的动平衡影响系数（转速为14040r/min）

从表4 和表5 中可以看出，在不同的原始不平衡条件下，加同样的试重，在同一个转速下计算得到的同一位置的动平衡影响系数差别很大。在转速7 560 r/min 时，同一位置影响系数的相位可相差50°以上，因为这是在一阶临界转速附近，谐响应的相位本身就处在急剧变化中，随着不平衡量的变化，临界转速也在变化，从而导致同一位置、同一转速下的影响系数差别很大。同样，在二阶临界转速附近（14 040 r/min），同一位置、同一转速下的影响系数差别也是很大的，例如凸台1 处的影响系数幅值差别达一倍以上。影响系数的差别从图5 中也可以直观地看出，在7 560 r/min 和14 040 r/min 附近，三条曲线对应的不平衡量成简单倍数关系，但谐响应的位移却明显不是简单的倍数关系。

同一位置、同一转速下的影响系数在不同的振幅下是不同的，这给动平衡、特别是高速动平衡带来了极大的麻烦，需要在动平衡时想办法解决这个问题。

3 结论

本文利用ANSYS 有限元分析软件建立了动力涡轮转子的转子动力学模型，分析了挤压油膜阻尼器变在不同偏心率、不同转速下的刚度阻尼系数变化情况，提出了一种考虑阻尼器偏心率和转速变化的变刚度阻尼系数不平衡谐响应计算方法，通过对计算结果的分析发现：由于转子不平衡量的增加，轴颈的振幅及阻尼器偏心率会增加，导致挤压油膜阻尼器的刚度和阻尼系数随之增加，最终导致转子系统的临界转速会随着不平衡量的增加而增加。同时，这也导致了同一位置、同一转速下，动平衡影响系数也会随着不平衡量的变化而变化，这给动平衡、特别是高速动平衡带来了很大的困扰。