达坂城河谷复杂地形风工程参数特性研究

苏小岚，辛 渝，张宏杰，余行杰，赵逸舟，李元鹏

(1.新疆维吾尔自治区气象服务中心，乌鲁木齐 830002；2.中国气象局乌鲁木齐沙漠气象研究所，乌鲁木齐 830002；3.中国电力科学研究院，北京 100055；4.新疆气候中心，乌鲁木齐 830002；5.新疆维吾尔自治区气象局，乌鲁木齐 830002)

引 言

发展可再生能源是应对气候变化,优化能源结构,解决能源和环境问题的关键。风能是一种可再生的清洁能源[1]，风力发电作为无污染可再生能源，已逐渐成为许多国家能源战略可持续发展的重要组成部分[2]。为了科学开发利用好风能资源，需要对当地风的特性及其对风电设备的影响开展分析研究。比如对风区中诸如风力机组选型设计、风机叶片的非定常载荷设计[3-8]等诸多规范中涉及的近地边界层内风的湍流特征，以及与风电机组转换效率设计和抗疲劳设计有关的风攻角等分布特征[6-9]及其对风电工程的影响等需要开展科学分析研究。我国对类似大型围栏、桥梁、风机等抗风设计中，湍流强度、阵风因子(Gu，下同)的估算，按平坦均匀下垫面4类动力学粗糙度(z0，下同)条件估算出离地10-200 m各高度层顺风向平均湍流强度(Iu，下同)、离地面5-300 m各高度层的Gu[10]。其中z0的区分，又主要按地物高矮稀密程度定性给出[10]。实际案例表明，z0自由度大，由z0推算得出的Gu或湍流强度非常粗糙[11]。另外，目前对非定常、非均匀的复杂下垫面在剧烈天气过程中对边界层气象要素影响的研究尚不成熟，相关的风观测研究及历史资料的积累极少。部分沿海区域及内陆对大风天气下的湍流研究，基本也仅基于单部测风塔上某高度上的三维超声风资料，垂直方向上含多层涡动相关的湍流观测理论的研究很少。其中，内陆复杂地形条件下或内陆强风风区湍流及其影响的观测更加薄弱[12-14]，许多仅是基于风廓线雷达探测资料阐明强风天气发生发展的机理研究，无法满足面向风工程抗风设计中风参数的设计要求[15-20]，因此有时需要借助CFD理想模型进行设计[9]。其次，除风攻角的计算方法在国际上统一外，各国针对不同应用领域，对同一风特性参数的计算也各异。这既反映了不同学科计算的风参数表征的侧重点不同[4-6]，也体现了实际风场中由于受z0、地形变化及热效应影响，湍流强度的时空分布缺乏规律性。由于风参数计算方法的多样性，也决定了实践中设计选择的复杂性。可见，面对重大建设工程规划，在参考各种规范或指南的基础上，结合现场案例观测研究和验证，延拓和补充过去因我国观测仪器限制而无法得到的风参数[12,21]势在必行。

新疆风能资源丰富[22]，在风能资源开发利用中，开展过风能资源数值模拟和预报方法研究、标量法下的湍流强度、风切变指数分析[23-25]，分析过新疆大风区气候变化趋势[26]和中性层结下大风区z0[27]；根据风区参证站资料均一性检验与订正[28]，参证站与测风塔同步测风数据相关分析，以及不同时距间日最大风速半经验公式换算的确定等，重新推算了新疆各风电场区域基准风压[29]等。新疆达板城河谷呈“U”型，内部地形地貌复杂[23-25]。宽为15～30 km不等，长约80 km，自西向东倾斜，渐次降低。河谷北侧博格达最高峰高达5445 m，地势较陡，为荒漠草原与草甸草原。南侧为天山支脉依连哈比尔尕山尾闾部分，距离河谷最近的最高山峰高约2600 m，山脚多为沙地。河谷内多灌木和半灌木荒漠、草甸和戈壁。内有盐湖、柴窝堡湖及四周的沼泽盐碱地，以及零星的人工绿洲等镶嵌其中(图1)。以全国第四次风能资源详查时沿谷底中心布设的测风塔为轴线，水平1 km分辨率的坡度角为1.5°～2.0°，柴窝堡气象站的坡度则达4.2°[23-24]。这种复杂地形和非均匀地表在夏半年最易驱动出强烈而特殊的局地风场，对风电场的安全运营及铁路、公路行车安全等将构成巨大威胁，对风电机组设计的经济化投入也带来不确定性。由于风力机和输电线路等在复杂山地又必须重视上升气流的影响[7,9]，因此有必要先从大气边界层角度，摸清该地与风工程紧密相关的参数的基本特征，勘验与我国推荐的行业设计规范中的特异性及其适用性，为今后结合不同行业应用需求，提高该地风工程设计中的研究应用水平奠定基础。限于观测资料，本研究将基于31003号[23-26]测风塔70 m高度上三维超声风资料，初步给出阵风因子、风攻角、不同等级湍流强度的气候特征。

1 资料来源及说明

1.1 观测环境、观测设置和仪器性能

31003(即D03)号测风塔位置见图1。与该风区另外两座测风塔所处环境相比，该测风塔所在环境最宽阔，但是离水体最近。31003号测风塔在10、30、50、70、100 m高度上可观测EL15型机械风杯测量的风向、风速。10和70 m高度上观测温度、湿度。70 m高度上塔架的东侧挑臂安装英国Gill公司生产的WindMaster Pro型三维超声风向风速传感器(仪器性能见表1)，承受雨强300 mm·h-1，竖向风速探头安装在挑臂上端1.2 m处。同高西侧装机械风速风向传感器。2个挑臂长度均为3 m。8.5 m高度上安装三维超声风向风速仪数据采集设备、电池、气压传感器等。

表1 WindMaster Pro型三维超声风向风速传感器关键特性

超声风数据采集器以UVW极坐标方式输出10 Hz频率的三维瞬时风速和声速声温。采集处理器上有质控判识码，每日自动生成一个数据文件。采用太阳能供电。通讯系统采用RS232、422、485等组网传输。

1.2 数据质控方法

所用资料时段为2011年全年。按常规结构风荷载设计应用需要，资料分析样本长度均以连续10 min时距为一个样本单元。先根据表1测量阈值和数据标识码进行“粗检验”，剔除无效值，剔除降水期间与后期两小时观测值，然后以Eddypro为辅助软件，进行“野点”判断标识，线性去趋和坐标旋转[30-31]；对于原始样本单元资料有效率达98.0%以上的序列，利用超声声温进行插补订正，否则不用。冬季受频率高的降雪和低温影响，资料利用率极低。

对于EL15型机械式梯度风数据中的“野点”数据判识方法，参见风电场风能资源测量方法(GB/T 18709-2002)[32]。

1.3 风参数计算方法

三维超声风资料坐标旋转、平均量、各方向脉动方差Ii(i=u,v,w)、风攻角α、阵风因子Gu等的计算参见文献[30,33-35]。EL15型平均风计算方法见GB/T 18709-2002[32]。

阵风因子Gu采用10 min样本单位内3 s平均风速的最大值与同期水平平均风速之比获得[10]。风攻角是指风的来向与水平面的夹角，计算式见文献[13]。具有攻角的风，长期作用会加速结构物的疲劳损伤和破坏，主要体现在强风时受不均匀地形影响。

2 结果分析

2.1 平均风速特征

2.1.1 不同等级平均风速的概率密度(PDF)分布

图2是基于超声风资料10 min时距平均风速(a)和日最大平均风速(b)的概率密度分布统计。由图2可见，70 m高度上10 min平均风速出现的概率呈双峰型，10.0～15.0 m·s-1的平均风速出现概率最高，约占40.0%，2.0～3.0 m·s-1的平均风速约占13.0%，15.0 m·s-1以上的平均风速约占20.0%。风机切出频率约达33.0%。日最大风速的概率分布近似呈单峰型，以10.0～22.0 m·s-1的最多，约占84.5%，其中，10 min平均风速≥17.0 m·s-1的大风日数高达44.0%。日常这类高频大风对超长、高耸建筑的耐久性及人类生活的舒适性均构成不利影响，同时对列车等交通运营安全也有较大影响。针对风机运营而言，此处风机切出风速频率也是较高的。

图2 2011年达坂城31003号测风塔70 m高度10 min时距平均风速(a)与日最大平均风速(b)的概率密度

2.1.2 不同等级平均风速的风向分布特征

图3(a)为超声风观测的≥1.5 m·s-1的10 min平均风速在不同方向上的分布。同时结合不同等级风速范围对应的风向概率分布玫瑰图(图略)可见：任何级别风速的风向都以西北偏西风或西北风最多，东南风次之，风向转换稳定。大风风向与峡谷地形走向一致。盛行西北风的风速略大于次多风向下的东南风风速。25 m·s-1以上的风全是西北风。西风强风风力不亚于登陆台风。

2.2 风攻角

本研究中风攻角正、负方向与三维超声风垂直风的观测方向一致,即超声风坐标旋转后的坐标中，垂直风速为负值时，为负攻角，否则为正攻角。对风机的动态失速和失速延迟模式设计而言，需要重点考虑正攻角对风机气动升力系数的影响，风攻角>5°的风电场，机翼设计的升力系数须显著提升[11]。可见，对于结构风工程的抗风设计而言，主要考虑大的正攻角影响。

图3(b)为超声风观测的≥1.5 m·s-1的10 min平均风速与风攻角的分布。可见，风攻角离散度与10 min平均风速大小有关。风速越大，风攻角的散布范围和风攻角的绝对值就越小。大的风攻角主要出现在相对低的风速段上。负攻角多于正攻角。特别是当风速超过25.0 m·s-1时，即西北风时，全为负攻角，在0～-3°变化。风速越大，风攻角绝对值的变率就越小，但非无限减小，而是趋于一定范围内的“平稳值”。

图3 2011年达坂城31003号测风塔70 m高度≥1.5 m·s-1的10 min平均风速在不同风向上的分布(a)及攻角分布(b)

为进一步区分平均风速、风向与风攻角的关系，本研究也分析了10 min平均风速≥1.5 m·s-1、≥4.0 m·s-1、≥6.0 m·s-1、≥8.0 m·s-1、≥10.0 m·s-1、≥12.0 m·s-1、≥15.0 m·s-1、≥18.0 m·s-1、≥20.0 m·s-1、≥25.0 m·s-1等不同等级风速下风向角和风攻角的分布特征。限于篇幅，也由于结构风工程中更多关注大风情况下的正攻角影响，在此仅遴选出10 min平均风速≥6.0 m·s-1、≥8.0 m·s-1、≥10.0 m·s-1、≥12.0 m·s-1时的风攻角分布(图4)。由图4可见，随着风速增加，风攻角大小随风向的分布渐次逼近与河谷走向一致的东南风和西北风2个方向上。东南大风时，正攻角频次达95.0%以上，西北大风时，负攻角频次达95.0%以上。这种正负显著差异主要是由2种截然不同的天气系统造成的。当出现东南大风时，主要由南、北疆之间的气压差造成，平均气流沿河谷向上游吹；而西北大风主要由自西向北入侵的冷空气受“狭管效应”影响，使流线加密产生，且叠加了高空气流沿倾斜度约1.5°～2.0°的河谷下沉造成[22-24,26]，使西北极端强风下对应高概率的负攻角。

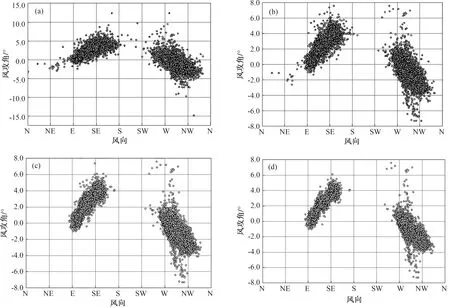
图4 2011年达坂城31003号测风塔70 m高度10 min平均风速≥6.0 m·s-1(a)、≥8.0 m·s-1(b)、≥10.0 m·s-1(c)、≥12.0 m·s-1(d)时风攻角随风向的分布

4 m·s-1以内的低风速段，偶尔存在风攻角大于15°的罕见现象，约占0.1%(图略)。对于风机机翼设计而言，结合图4各等级风速下不同风向的风攻角分布也可见，平均风速为3.0～15.0 m·s-1的风机启动风速内，风攻角大于5°的比例也较高，盛行风向与次多风向都存在这种大攻角。因此，对风机制造者而言，需要从技术上提高此处风机的气动升力系数及风力转换率，降低风机的老化速度。风攻角大于5°的概率，总计约占1.0%;平均风速≥6.0 m·s-1的风速段，风攻角大于3°的比例，高达5.7%。总之，达坂城平均风速≥6.0 m·s-1时伴随的正攻角，对此处风力机的使用寿命影响最大。

2.3 风的湍流参数特征

2.3.1 阵风因子Gu

图5为2011年达坂城31003号测风塔70 m高度阵风因子与>1.5 m·s-1的10 min平均风速的概率分布。由图5可见，与风攻角和平均风速之间的关系类似，Gu的离散度随着风速的增加而降低。平均风速越大，Gu变率就越小，也是直到减小到某一范围内的“稳定值”为止。结合不同等级风速下Gu分布概率密度图(图略)也可知，当平均风速≥4.0 m·s-1、≥6.0 m·s-1、或≥8.0 m·s-1时，Gu在1.0～1.4变化的概率最高；平均风速≥10.0 m·s-1、≥12.0 m·s-1、或≥15.0 m·s-1时，Gu在1.0～1.2变化的概率最高；平均风速≥18.0 m·s-1时，Gu在1.1～1.2变化的概率最高。总体而言，平均风速为10.0 m·s-1以上时，各等级风速Gu随风速增加而变化的范围多数为1.1～1.7；在平均风速≥20.0 m·s-1的“极端强风风速[25]”下，Gu变化范围多数为1.0～1.4。图6给出了10 min平均风速≥10.0 m·s-1、≥15.0 m·s-1、≥20.0 m·s-1、≥25.0 m·s-1等风速下不同风向的Gu分布特征。由图6可见，风速越大，Gu的相对大值集中在盛行风与次多风向上的概率越高。沿盛行风向(西到西北扇区)的Gu总比次风向(东到东南扇区)偏大，特别是平均风速≥12.0 m·s-1(图略)时，这种差异更加明显。当平均风速≥25.0 m·s-1时，Gu大多为1.1～1.2，约占94.6%；1.3～1.4的Gu约占5.0%；最大达1.7，对应10 min平均风速高达26.6 m·s-1；平均风速达21.0 m·s-1以上、且阵风因子高于我国《建筑结构荷载规范》B类下垫面设计值(1.52)[36]的现象分别出现在2010年12月11日22时40分和2010年12月24日04时30分的强风样本中。可见，该处阵风因子按B类设计可能偏于不安全。

图5 2011年达坂城31003号测风塔70 m高度Gu与>1.5 m·s-1的10 min平均风速的概率分布

图6 2011年达坂城31003号测风塔70 m高度10 min平均风速≥10.0 m·s-1(a)、≥15.0 m·s-1(b)、≥20.0 m·s-1(c)、≥25.0 m·s-1(d)时Gu随风向的分布

2.3.2 湍流强度

图7(a)(b)(c)分别为2011年达坂城31003号测风塔70 m高度Iu、Iv、Iw与>1.5 m·s-1的10 min平均风速的概率分布。由图7可见，各方向湍流强度随平均风速的变化与阵风因子、风攻角等的散布特点也相似：随着风速的增加，各方向湍流强度及其离散程度均呈下降趋势，风速越大，变率越小；当平均风速增加到20 m·s-1以上时，各方向湍流强度略呈增加趋势，这一点与风攻角和阵风因子随风速增加而减小的趋势略有不同。平均风速≥10 m·s-1时，顺风向偶尔还会出现大的湍流强度；平均来讲，1.5 m·s-1以上平均风的湍流强度在3个方向的相对比值为Iu∶Iv∶Iw=1.00∶0.85∶0.54，平均Iu=0.10。而我国风荷载规范推算为Iu∶Iv∶Iw=1.00∶0.88∶0.50，平均Iu=0.14。可见，平均的横风向湍流强度比顺风向偏弱的幅度比风荷载规范推算的偏小，而竖直方向机械湍流或热力湍流强度比规范估算的偏强。工程上需重点考虑顺风向与竖直方向的湍流尺度和湍流功率密度的影响。从不同等级风速下各方向湍流强度分布的概率密度(图略)可见，当平均风速超过4.0 m s-1时，Iu、Iv和Iw分别超过0.20、0.10和0.08的概率都很小，Iu、Iv和Iw出现频率最高的分别在0.08～0.10、0.05～0.10和0.05～0.10的区间，即顺风方向的湍流强度变率最大，这一点可从图7的对比中看到。在极端强风条件下，顺风向湍流强度随平均风速的分布特征与阵风因子的变化完全吻合：当平均风速≥25.0 m·s-1时，Iu大多为0.05～0.08，约占94.6%，其余的为0.14～0.19，出现了明显的非连续现象。

图7 2011年达坂城31003号测风塔70 m高度Iu(a)、Iv(b)、Iw(c)与>1.5 m·s-1的10 min平均风速的概率分布

图8(a)(b)为2011年达坂城31003号测风塔70 m高度Iv/Iu和Iw/Iu与>1.5 m·s-1的10 min平均风速的概率分布。由图8可见，与上述相似，各方向湍流强度比值Iv/Iu和Iw/Iu的离散度也很大。低风速时，Iv/Iu和Iw/Iu值大于高风速时的比值。随着风速增加，各方向湍流强度及其离散程度都呈下降趋势。大风时的大湍流强度主要体现在顺风向上。当平均风速在10.0 m·s-1以下时，Iv/Iu和Iw/Iu比值偶尔会出现分别超过4.0和1.5的现象，主要是因为在这个风速段上除了盛行由南北疆之间的气压梯度力作用下的“东南大风”影响外，还受局地“湖陆风效应”影响：距此测风塔西南方位近4 km的地方，有一个大约28 km2的湖泊——达坂城“柴窝堡湖”，当主导天气系统偏弱，局地以热成风为主的“湖陆风环流”为主导因素时，横风向的湍流强度就比顺风向的偏强。

图8 2011年达坂城31003号测风塔70 m高度Iv/Iu(a)、Iw/Iu(b)与>1.5 m·s-1的10 min平均风速的概率分布

多数情况下，Iv/Iu和Iw/Iu的值小于1.0，分别约占65.0%、95.0%。平均风速小于7.0 m·s-1时，Iv/Iu随风速增加，比值略呈下降趋势；平均风速介于7.0～11.0 m·s-1时，比值为0.90～0.92；平均风速介于11.0～24.0 m·s-1时，随着风速的增加，比值由0.88下降到0.66；平均风速>24.0 m·s-1时，比值波动范围为0.59～0.72。风速越大，顺风方向的湍流强度相对就越强。Iw/Iu在各等级风速下的比值随风速增加而变化的情形略有不同：风速<27 m·s-1时，比值随风速的增加呈下降趋势；风速≥27 m·s-1时，随风速的增加，比值反而略呈上升趋势，由0.40上升到0.44。再一次说明出现极端强风时，竖向湍流也在增强。

另外，从不同风速段Iv/Iu和Iw/Iu的概率分布密度图(图略)也可看出，平均风速≥4.0 m·s-1时，Iv/Iu和Iw/Iu分别超过1.3和0.8的概率很小。对于Iv/Iu，平均风速分别≥1.5 m·s-1、≥4.0 m·s-1和≥6.0 m·s-1时，发生概率最大的值均约为0.75；≥8.0 m·s-1时，发生概率最大的值约为0.70。对于Iw/Iu，平均风速分别>1.5 m·s-1、>4.0 m·s-1和>6.0 m·s-1时，发生概率最大的比值均约为0.45；≥8.0 m·s-1时，发生概率最大的比值约为0.40。“高风”时沿顺风方向的湍流强度比横向风的高得多，且无论哪个风速量级，计算的Iu∶Iv∶Iw均不满足风荷载规范推荐采用的Iu∶Iv∶Iw=1.00∶0.88∶0.50。

2.4 平均风的垂直变化特征

由于近地层较薄，可以近似地认为动量、热量和水汽的垂直湍流输送量几乎不随高度变化及风向也不随高度变化的常值通量层，故在此不对风向随高度的变化进行分析，仅分析5层梯度风观测高度上平均风速随高度的变化特征(图略)。10 m高度上的平均风速高达8.0 m·s-1以上。100 m以下，平均风速随高度的增加而增加，基本符合中性条件下，风随高度呈幂指数变化的规律，但在50-70 m高度上有一“拐点”：平均风速随高度稍变。这在风能资源开发利用中，对风机轮毂高度或者风机叶根长度的最佳设计时，值得高度关注，同时基于目前对该地边界层的平均厚度认识不清，或边界层厚度与湍流的关系尚无定量化的前提下，无须盲目提高风机轮毂高度。

3 结论与讨论

本研究根据2011年全年三维超声风资料和5层梯度风资料，给出了该地近地层风参数的基本特征：

(1)70 m高度上10 min平均风速出现的概率呈双峰型，10.0～15.0 m·s-1的平均风速出现概率最高，约占40.0%，2.0～3.0 m·s-1的平均风速约占13.0%，15.0 m·s-1以上的平均风速约占20.0%，风机切出频率约达33.0%。日最大风速以10.0～22.0 m·s-1占绝大多数，约84.5%。其中，10 min平均风速≥17.0 m·s-1的大风日数高达44.0%。西北盛行风向与东南次多风向概率相当。100 m以下，平均风速随高度增加而增加，但在50-70 m高度上，平均风速随高度少变，风机轮毂高度不宜盲目提高。

(2)平均风速≥25.0 m·s-1时，阵风因子大多为1.1～1.2，约占94.6%；达1.3～1.4的阵风因子，约占5.0%；最大的达1.7，对应10 min平均风速为26.6 m·s-1。顺风向湍流强度大多为0.05～0.08，约占94.6%，其余的为0.14～0.19，出现了明显的非连续现象。阵风因子与湍流强度在21.0 m·s-1以上极端强风情况下，表现出了与风速大小关系不大的现象，且观测期内两度出现阵风因子比我国《建筑荷载规范》B类下垫面70 m高度上的设计值偏高现象。

(3)风攻角正负变化的位相与盛行风向与次多风向的转换一致，且负攻角多于正攻角。平均风速为3.0～15.0 m·s-1的风机启动风速内，盛行风向与次多风向的风攻角大于5°的概率约占1.0%，对风机制造者而言，需考虑提高此处风机的升力系数，降低风机老化速度，提高功率输出。

(4)平均的脉动风湍流强度遵循Iu∶Iv∶Iw=1.00∶0.85∶0.54，平均Iu=0.10。这与我国风荷载规范推算的Iu∶Iv∶Iw=1.00∶0.88∶0.50，平均Iu=0.14，略有不符。平均顺风向湍流强度与沿海受台风影响区域的相当，需重点考虑顺风向湍流参数影响。