变后掠翼的参变气动弹性建模与分析1)

张立启 岳承宇 赵永辉

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

引言

固定翼飞机一直面临着高速和低速飞行性能要求的矛盾:后掠翼可以有效降低激波阻力，但在亚音速状态下飞行效率低;平直机翼在低速飞行时具有较好的飞行性能，但在跨音速区域，受到的激波阻力却急剧增长.变后掠机翼可同时兼顾高低速两个方面的要求.从20 世纪30 年代以来，变后掠翼飞机经历了长达近百年的发展.早期的Pterodactyl IV 验证机、F-14 战斗机、Tornado 战斗机和Tu-160 轰炸机均实现了主动改变机翼后掠角而带来的飞行性能提升.然而，增加飞机重量和结构复杂度的缺点使变后掠翼在20 世纪70 年代后的发展与应用陷入停滞.2003 年，美国国防部先进研究计划局(DAPRA)启动“变体飞行器结构(MAS) ”研究计划，重新掀起了变体机翼的研究热潮[1-3].受此计划的鼓舞，一些关于变后掠翼的新概念性设计浮现出来，比如美国佛罗里达大学研制的独立多关节变后掠翼，新一代航空技术公司研制的验证无人机MFX-1 和MFX-2.与早期研究不同，当前变后掠翼的研究重点倾向于高性能材料(比如柔性蒙皮)和驱动装置(比如智能结构、柔顺机构)的设计和使用.

目前，固定翼下的气动弹性系统建模已经成熟，ZAERO 软件和NASTRAN 中的气动弹性分析模块均可对固定翼飞行器进行颤振速度的计算和动态响应分析.而在可变后掠机翼的气动弹性建模和分析方面的研究较少.飞行器在变体过程中，系统的动力学特性随着变体控制参数的变化而变化，相应的气动弹性方程本质上是随参数时变的.对于参数慢变情形，可采用时间冻结法，获得某一变体参数下的气动弹性模型.

在变体飞机方面，Zhao 和Hu[4]和Huang 等[5]提出了一种利用子结构综合和偶极子网格法构建折叠翼的参数化气动弹性建模方法，可对不同构型下的折叠翼实现快速的颤振分析，分析结果发现对于不同折叠角下的机翼其气动弹性特征将发生显著改变.Hu 等[6]在此基础上采用Krigin 代理模型技术对不同后掠角下的空气动力影响矩阵进行插值，获得了参数化的气动弹性模型并研究了折叠翼变形过程中的时变气动弹性响应.Xu 等[7]利用ADAMS 对折叠翼进行柔性多体动力学建模，将不同后掠角下的非定常气动力进行插值后与结构进行耦合，计算分析了折叠翼快速展开过程中的瞬态响应.詹玖榆等[8]利用流形插值技术[9]对模态坐标下不同构型折叠翼的刚度矩阵、质量矩阵和振型矩阵进行插值，建立了参数化的结构动力学模型，并将其与偶极子网格法相结合计算了折叠翼的气动弹性行为.

对可变后掠翼，大量的研究集中在最优变形规律以及变后掠翼气动布局等方面，对于可变后掠翼的参变气动弹性系统建模方法和慢时变气动弹性方面的研究依然匮乏，变后掠过程中准确而高效地计算气动弹性响应仍是一项具有挑战性的工作.由于变后掠翼在结构变体过程中参数是变化的，使得参变气动弹性系统的建模存在一定困难.线性参变系统(linear parameter varying，LPV)[10]模型可以用来描述受时变参数影响的线性系统的动力特征，也可以用一系列当地线性模型来表征非线性系统.一般地，LPV 建模方法有两种:全局建模方法[11-13]和当地建模方法[14-15].利用全局模型能够进行全局参变的研究，即任意激励下结构持续参变过程中的动态响应研究.显然，这一要求比较苛刻，一般很难实现[16];后者则是利用当地建模技术，采用时间冻结法，在不同固定参数下生成当地的线性时不变(linear time invariant，LTI)模型，然后对这些LTI 模型进行合理的插值来建立线性参变模型.利用当地建模技术建立LPV 模型的方法要求所建立的当地LTI 模型必须具有一致的状态空间形式.若直接对系统矩阵进行插值可能带来很大风险甚至得到错误的状态空间模型，这是由于同一系统的状态空间实现并不唯一，导致不同参数点处的状态空间表达并不具有一致性.上述研究均未能讨论和考虑模型的一致性问题.

Paige[17]和Wassink 等[18]着重强调了不一致的LTI 状态空间表达式对于当地LPV 模型实际应用的影响和限制.因此，如何有效的解决当地模型之间的不一致问题，便成为了当地LPV 模型能否成功运用的关键.Paijmans 等[19]提出了一种依赖于仿射参数空间实现的LPV 建模技术，该方法需要对当地模型的极点和零点的轨迹进行排序和拟合.Caigy 等[20]提出了一种单输入单输出(single input single output，SISO)的LPV 建模方法，该方法需要划分多个子模型.Caigy 等[21]将当地LTI 模型划分为一系列当地子模型[19-20]的方法推广到多输入多输出(multiple input multiple output，MIMO)情况，对当地模型的极点和零点进行排序，将原始的当地模型分解为一个增益与一阶和二阶子模型状态空间串联的形式，得到了一致的状态空间表达式.Krolick 等[22]提出了一种基于数据驱动的模型降阶方法，并探讨了不同参数下模型的一致性问题，发现利用自回归(autoregressive exogenous，ARX)方法建立的参数化模型一致性较好.Goizueta 等[23]利用Krylov 子空间来构造线性转换矩阵，解决了LTI 模型不一致问题.

以上方法均是从已知的、参数空间中离散点处的、不一致的状态空间方程出发，通过对状态空间方程的一致性处理来获得参变系统状态空间模型的.本文则从另一种角度出发:即在构造参变空间内离散点处的状态空间模型之前就解决可能存在的不一致性问题.因而后续所建立的、离散点处的状态空间模型就是一致的，参变空间内任意点处的状态空间模型便可通过对一致的当地模型进行插值得到.可通过数值结果验证了本文方法的正确性和有效性.本文采用当地气动弹性建模技术，深入研究了如何建立一致的当地气动弹性状态方程的可靠方法，以期为MIMO 的参变气动弹性系统建模提供参考数据.

1 变后掠翼的参数化结构动力学建模

变后掠翼如图1 所示.机翼采用旋转-剪切变后掠设计，翼肋在变后掠过程中保持顺气流翼型不变.机翼的结构设计参数为:翼根弦长758.3 mm，翼尖弦长283.3 mm，平均弦长346.4 mm，半展长1718.0 mm，机翼面积0.595 7 m2，重量20.23 kg.机翼的前缘后掠角χ可在 0°(完全平直状态)到 60 °(大后掠角状态)范围内变化.

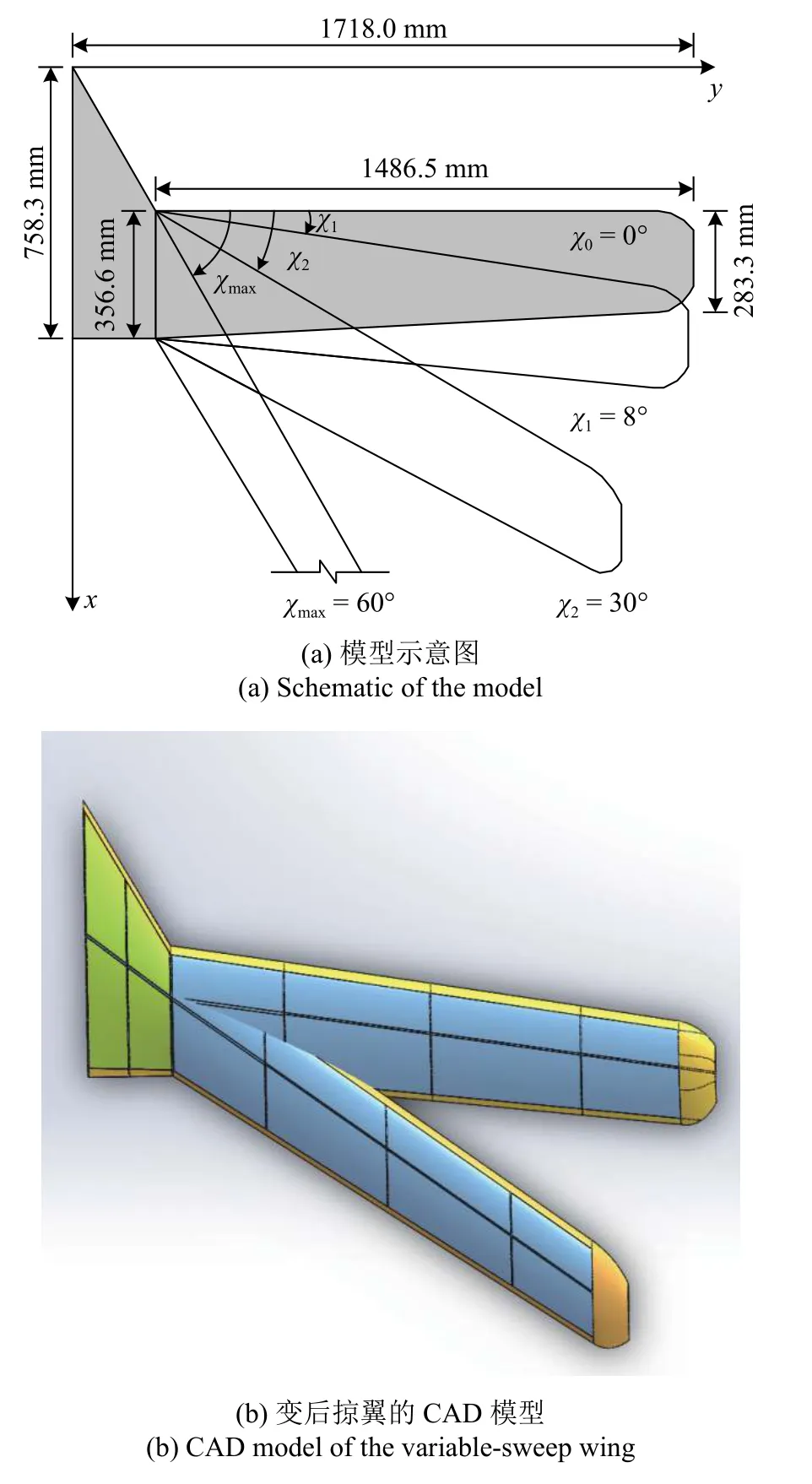
图1 变后掠翼的几何模型Fig.1 Geometric model of the variable-sweep wing

后掠翼的运动方程依赖于后掠角χ这一控制参数.常规有限元建模方法只适用于固定构型情形.如需获得不同后掠角下的有限元模型则需要进行大量的重复性建模工作，过程十分繁琐，效率低下.本文采用如下参数化自动建模方案:仅在χ=8 °下建立原始结构的有限元模型(如图2 所示)，使用自编程序读取该结构结点和单元数据;给定任意后掠角后，该角度下的有限元结点位置可由原始模型中的结点位置经过坐标旋转获得，进而直接生成BDF 数据文件并提交至NASTRAN，自动进行结构固有振动分析，为参变气动弹性系统的建模提供结构固有振动特性数据.如图2 所示，机翼共划分为 3 369 个单元，结构采用板、杆、梁和集中质量单元构建，翼梁和翼肋采用板单元和杆单元相结合的方式建模，蒙皮采用板单元.

图2 变后掠翼的有限元模型(χ =8°)Fig.2 Finite element model of the variable-sweep wing (χ =8°)

机翼结构的边界条件为翼根固支.表1 给出了χ=8°时结构的前6 阶固有频率，图3 为相应的固有振型.由于机翼展弦比较大，前6 阶模态中包含面内运动模态(第2 阶).

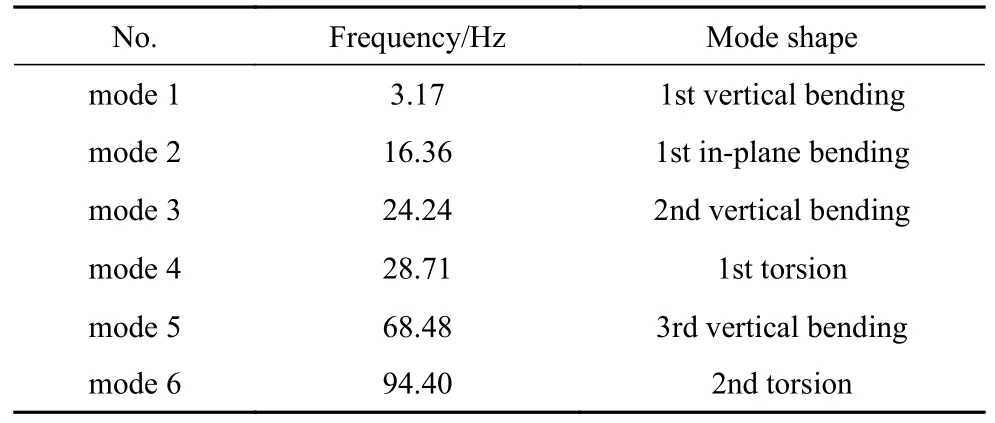
表1 变后掠翼的前6 阶固有模态(χ =8°)Table 1 The first six natural modes (χ =8°)

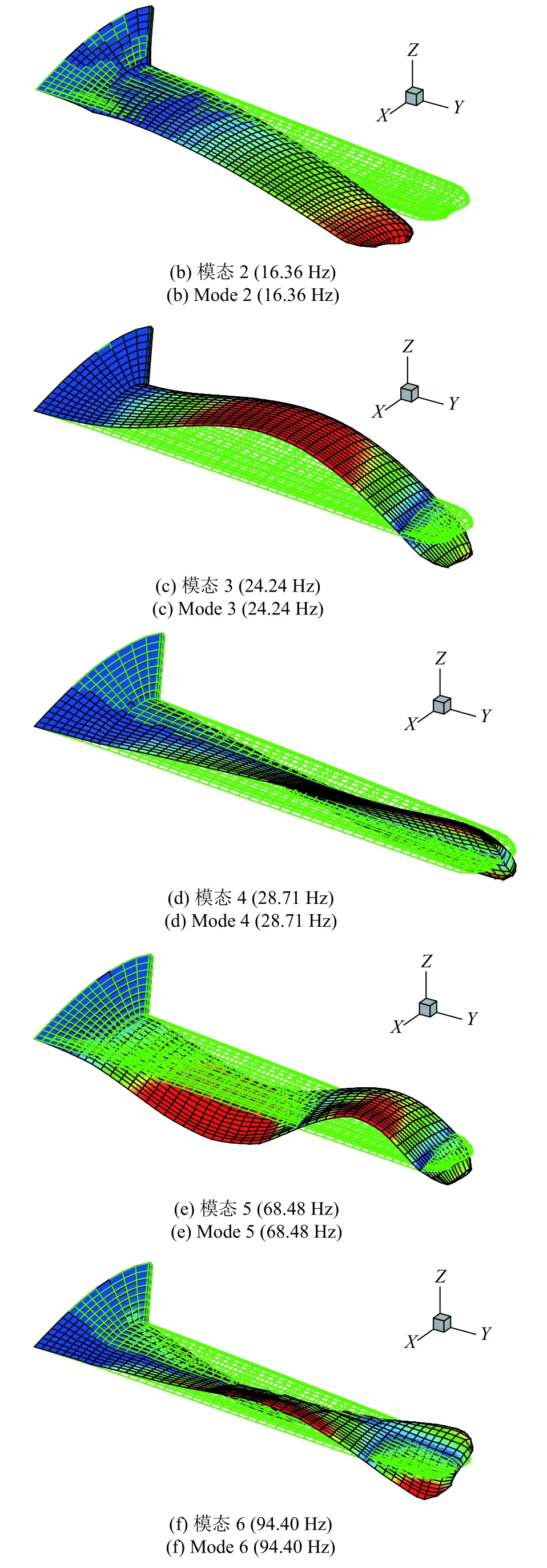
图3 变后掠翼的前6 阶固有振型(χ=8°)Fig.3 The first six mode shapes of the variable-sweep wing (χ=8°)

根据前述的结构参数化建模方案，任意后掠角下的有限元模型都可以方便地利用NASTRAN 生成.建模的结果包含结构整体质量矩阵、刚度矩阵、固有模态矩阵以及结点坐标等模型信息.这些数据将在自编程序中进一步处理生成机翼的气动弹性模型.在后掠角0°～ 60°的变化范围内，每隔 5 °计算出机翼的固有振动特性，机翼的前6 阶固有频率如表2 所示.

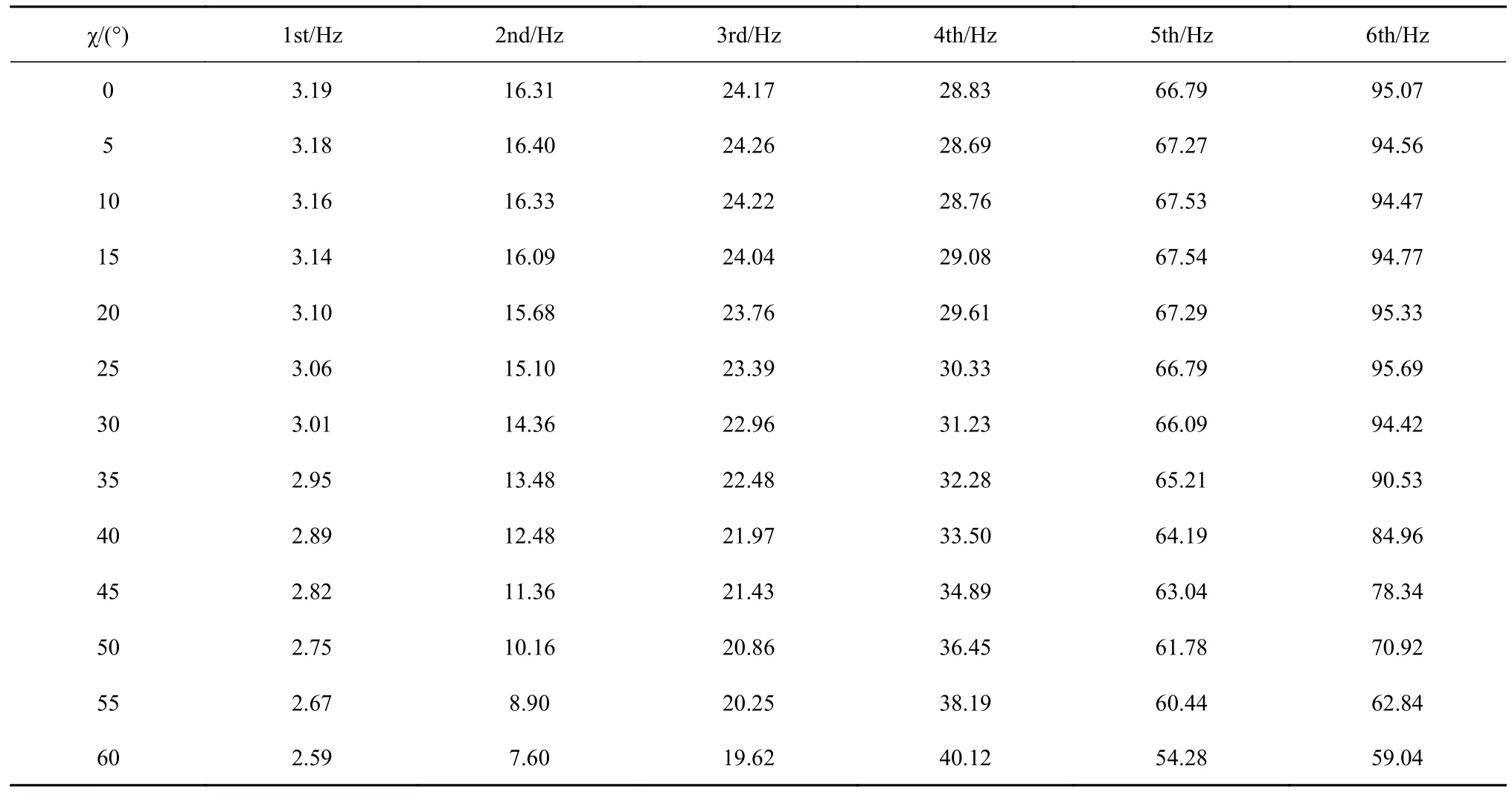
表2 不同后掠角下机翼的前6 阶固有频率Table 2 The first six order natural frequencies of the wing at different swept angles

2 固定后掠角下的气动弹性模型

采用基于偶极子网格法(doublet lattice method，DLM)的非定常气动力模型[24].DLM 将机翼视为无厚度升力面，并将升力面划分为若干个与来流方向平行的空气动力网格，如图4 所示.与结构有限元模型的参数化建模方法类似，在建立非定常气动模型时，仅在χ=8 °下划分气动网格，共计799 个网格单元，其他任意后掠角下的气动网格均可根据原始网格通过坐标旋转获得.

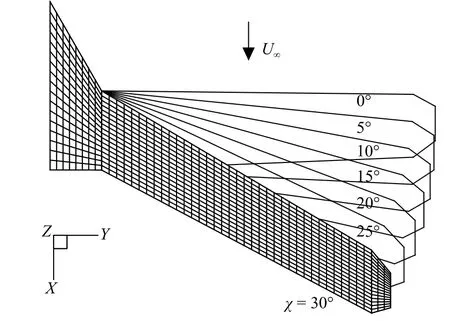
图4 变后掠翼在不同后掠角下的空气动力网格Fig.4 Aerodynamic boxes on the lifting surface of the variable-sweep wing

根据DLM 模型计算得到升力面的空气动力影响系数(aerodynamic influence coefficient，AIC)矩阵，根据非穿透边界条件建立简谐运动情况下全部气动网格上的压力系数与网格控制点处无量纲下洗速度之间的关系.然后通过样条插值将非定常气动力等效到结构结点上.变后掠翼的气动弹性方程可写为如下形式

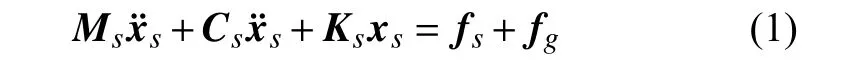
式中，xs为结点位移向量，Ms，Cs和Ks分别为质量矩阵、阻尼矩阵和刚度矩阵.fs，fg分别为结构运动与突风扰动引起的非定常气动力，具有如下形式[25]

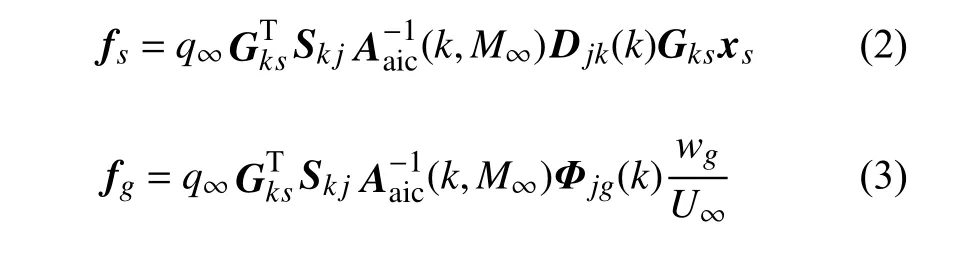
式中，U∞为来流流速度，q∞为来流动压，Gks为样条矩阵.Skj为气动网格积分矩阵，Djk为物质导数矩阵. Φjg为突风模态向量，包含简谐突风激励对各气动网格的作用比值.Aaic为AIC 矩阵，与减缩频率k与马赫数M∞相关.wg为参考点处的突风速度扰动.

引入模态坐标变换xs=Φhξ，将式(1)转换至模态坐标中，表示如下

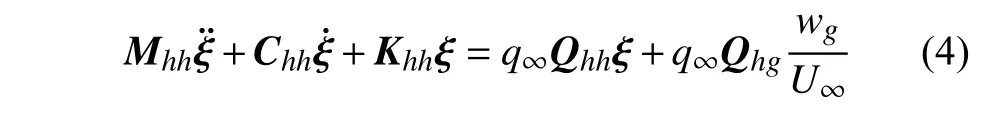
式中，Φh为结构模态矩阵，ξ 为相应的结构模态位移.Mhh，Chh和Khh分别为模态质量、模态阻尼和模态刚度矩阵.Qhh，Qhg分别与结构运动和突风扰动有关的广义空气动力(generalize aerodynamics force，GAF)矩阵.以上各矩阵的具体表达式为

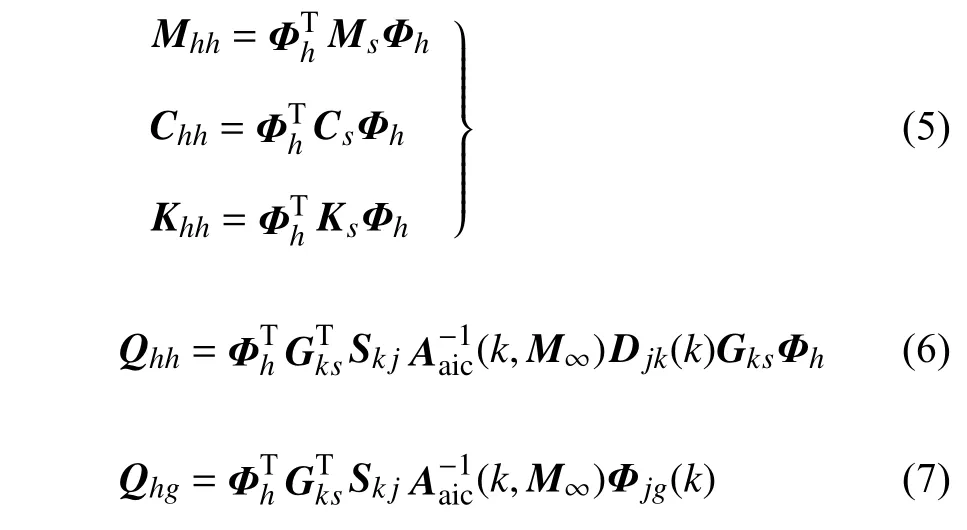
式(4)中的GAF 矩阵为频域形式，如果进行时域气动弹性分析，可以通过有理函数拟合(rational functional approximation，RFA)技术将GAF 矩阵转换至拉氏域，然后再转化到时域.然而，当前固定后掠角下的气动弹性模型并不适合在时变角度下做仿真计算，因为对每个时间步，在线计算结构模态矩阵和非定常气动力矩阵是非常低效的.下一节将提出一种基于当地气动弹性模型的插值建模技术，其优点是能够快速获得参数空间内任意一点的气动弹性模型.

3 基于当地模型插值的参变系统建模方法

变后掠翼的气动弹性分析和响应计算均可在LPV 系统的框架内进行，当地建模技术是构造LPV系统的一种实用且高效的建模手段[26].首先对参数变化空间进行离散处理，然后在各离散参数点处分别建立一系列线性时不变(LTI)系统模型，最后对这些LTI 模型进行插值，从而快速获得参数空间内任意一点处的LTI 模型.在参数慢变的假设下，LTI 模型中缺少的动态参数依赖部分可以忽略不计[27]，本文采用此假设.将插值步骤融入仿真过程，即可对可变后掠翼进行慢时变响应计算.

然而，使用当地建模技术时，各当地模型必须事先处理为一致的形式，否则将得到错误的插值后系统.考察式(4)给出的气动弹性方程，各矩阵均与结构模态矩阵 Φh有关，而 Φh是随后掠角变化的.一方面，对于参变系统来说，随着参数的变化，可能存在所谓的“模态交叉”现象，此时交叉点前后同一模态分支(相似的振动形态)的阶次将发生变化，具体表现为矩阵 Φh的数值上的跳跃，此时不经处理直接按照默认模态阶次进行插值是错误的;另一方面，RFA 的近似过程中需迭代求解非线性最小二乘问题，算法具有数值不稳定的特点，非常容易造成连续变化的后掠角对应不连续的拟合系数矩阵的情况，在这种情形下生成的当地模型同样不能进行直接插值.本文分别针对结构和气动这两方面可能存在的不一致性问题给出了相应的一致性处理方法.该方法能够保证在参数空间内生成一致的当地气动弹性模型.

3.1 模态匹配和对齐

为获得后掠翼模态数据，在nt个离散的后掠角χ1，χ2，···，χnt处建立后掠翼的结构动力学模型，求解以下广义特征值问题

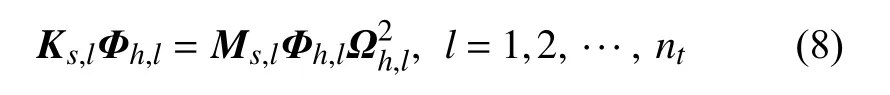
式中，Ωh，l为结构固有频率构成的对角阵，矩阵Φh，l的列向量为按模态质量归一化的结构固有振型.

一般情况下，特征值和特征向量通常简单地按照大小排列顺序.当存在模态交叉时，同一阶次的模态振型由于模态性质不同而不能直接用来插值.插值应该在同一条模态分支上进行，而同一条模态分支上的模态具有相似的振动形态，因此对相邻参数点下的固有频率和振型进行比较，有望将 Φh，l中的振型调整为匹配的顺序.考察两个相邻的后掠角χl-1和χl，定义如下距离度量来衡量相邻的两个角度下模态之间的接近程度

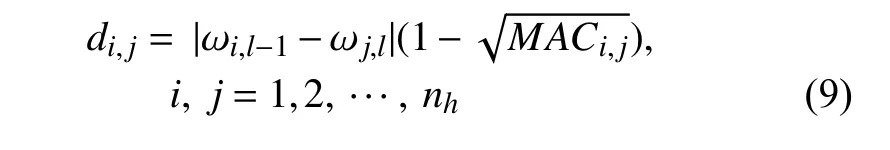
式中，ωi，l-1和 ωj，l分别为l-1和l点处的第i个和第j个固有频率，nh为保留的结构模态数量，MAC为模态置信准则，按照下式计算

式中，φi，l-1和 φj，l分别为l-1和l点处的第i个和第j个固有振型向量.

距离度量式(9)使用了两个固有频率之间的直线距离，并用MAC 加权.MAC 在区间[0，1]之间取值，其值越大则表明固有振型之间的线性相关性越高.假设l-1 点处的模态数据具有正确的顺序，模态匹配的任务是将l点处的模态数据与l-1 点进行配对，正确的配对应使总的距离度量最小.基于图论，将待考察的模态划分成以下两组顶点

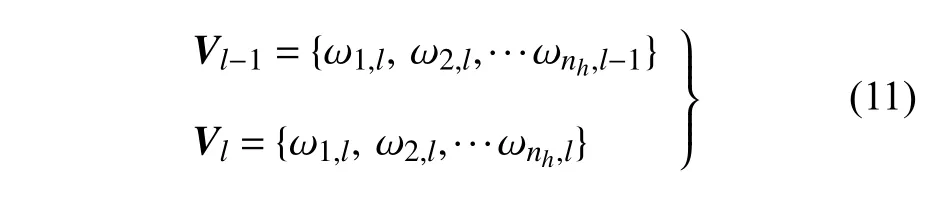
定义边集El=Vl-1×Vl，即任意两个Vl-1和Vl中的顶点都有唯一的边相连，从而构成一个完全二分图Gl=(Vl-1，Vl;El).距离度量式(9) 给出了每条边对应的费用.模态匹配问题可转换为寻找图Gl的一个完美匹配使费用总和最小，这个问题又称为线性求和分配问题(linear sum assignment problem，LSAP)[28].匈牙利算法是求解LSAP 的标准方法，该算法由Kuhn 首先提出.目前广泛采用Jonker 和Volgennant 开发的基于最短增广路径技术的改进算法[29]，使线性求和分配问题的求解达到O() 的最坏情况时间复杂度.

为了保证数值连续变化，固有振型向量的正负符号问题也应顺带处理.将重新排列后的固有振型向量调整为ci，jφj，l，其中符号系数ci，j按照下式计算

通过模态匹配与对齐，能够保证式(4)中建立的气动弹性模型在全部后掠角下都有一致的形式.

3.2 一致的有理函数表达式

另一可能引起模型不一致的因素是非定常气动力的有理函数近似.为获得时域的气动弹性方程，需要通过RFA 技术将频域气动力扩展至Laplace 域.RFA 技术利用一系列减缩频率下的GAF 数据拟合特定形式的有理函数，其中最常用是下式给出的最小状态近似(minimum state approximation，MSA)

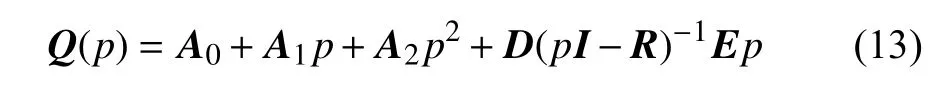
式中，p为复减缩频率，Q为GAF 矩阵Qhh和Qhg的组合，R为由空气动力滞后根组成的对角阵.其余矩阵通过迭代求解非线性最小二乘问题获得.虽然求解过程得到了确定的有理函数表达式，但是滞后项中D和E矩阵是不唯一的.一般地，对于任意可逆矩阵T，下式始终成立

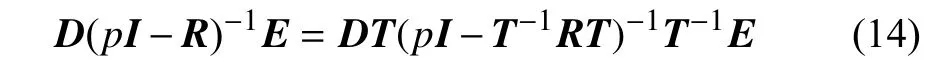
在建立可变后掠角气动弹性系统模型时，拟合后的系数矩阵的不唯一性会造成当地气动力模型之间的不一致，从而导致插值得到的系统是错误的.由于R矩阵事先给定且为对角阵，为保证R矩阵不变，易知T矩阵也必须限制为对角阵.因此，有理函数拟合的不唯一性表现在对D和E矩阵的列向量和行向量的任意缩放.假设R矩阵不随参数变化或者随参数连续变化，那么可以根据相邻参数下的有理函数拟合结果构造出唯一的缩放矩阵T，从而得到唯一且连续的有理函数表达式.

考虑相邻两个后掠角χl-1和χl，以l-1点处的Dl矩阵为标准参照，l点处的对角阵Tl根据下式进行构造

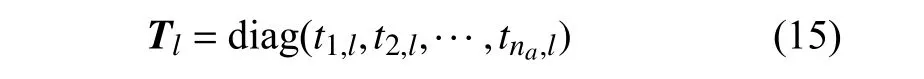
式中，na为空气动力滞后根的数量，对角元ti，l的计算方法如下

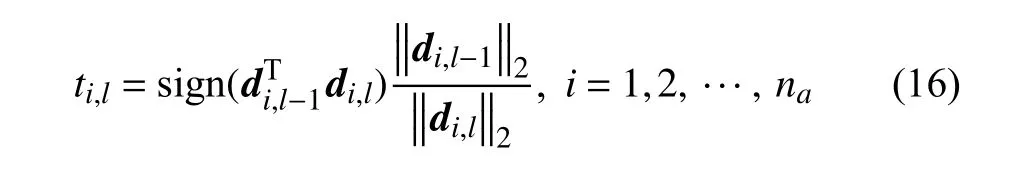
式中，di，l-1和di，l分别为矩阵Dl-1和Dl的第i列.得到Ti后根据式(14)调整矩阵Dl和El，调整后的矩阵Dl与参照矩阵Dl-1的列向量有相同的2 范数和一致的方向.

如后掠角和马赫数均为可变参数，此时RFA 原始数据在二维参数网格上生成.这种情况下一致性处理方法应该是:首先固定第一个马赫数，按照后掠角顺序依次调整系数矩阵;随后固定各个后掠角，再按照马赫数的顺序使用相同的方法依次调整系数矩阵.

经过模态匹配的气动弹性方程式(4)与使用一致RFA 表达的式(13)相结合，再按照传统气动伺服弹性系统的构造方式，最终生成如下时域状态空间系统方程[25]

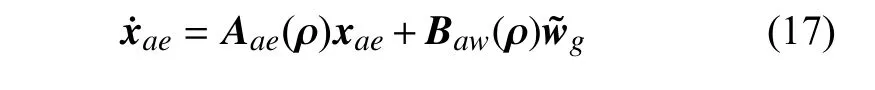
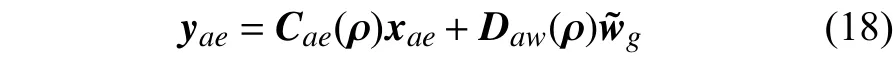
式中，参数向量 ρ 包括后掠角χ和飞行参数.状态变量xae包含结构模态位移 ξ 和模态速度，以及有理函数近似的引入的空气动力状态变量.突风扰动为突风速度wg及其时间导数构成的向量，多种突风模型可用于生成标准化的突风扰动信号[30].系统输出yae可以是结构某监控结点的响应或内载荷响应，输出矩阵以及状态空间矩阵具体的构造方法参考文献[31].

利用本文给出的模态匹配和RFA 系数处理方法，可解决变后掠翼当地气动弹性模型中可能出现的不一致性问题.不论是后掠角还是飞行参数的改变，各当地系统矩阵都能保证随参数连续变化.图5 总结了本文提出了基于当地建模技术的变后掠翼参变气动弹性系统的建模流程.对一致的当地模型进行插值，能够快速获取任意后掠角下的状态空间矩阵，大大提高时变气动弹性分析与响应计算的效率.

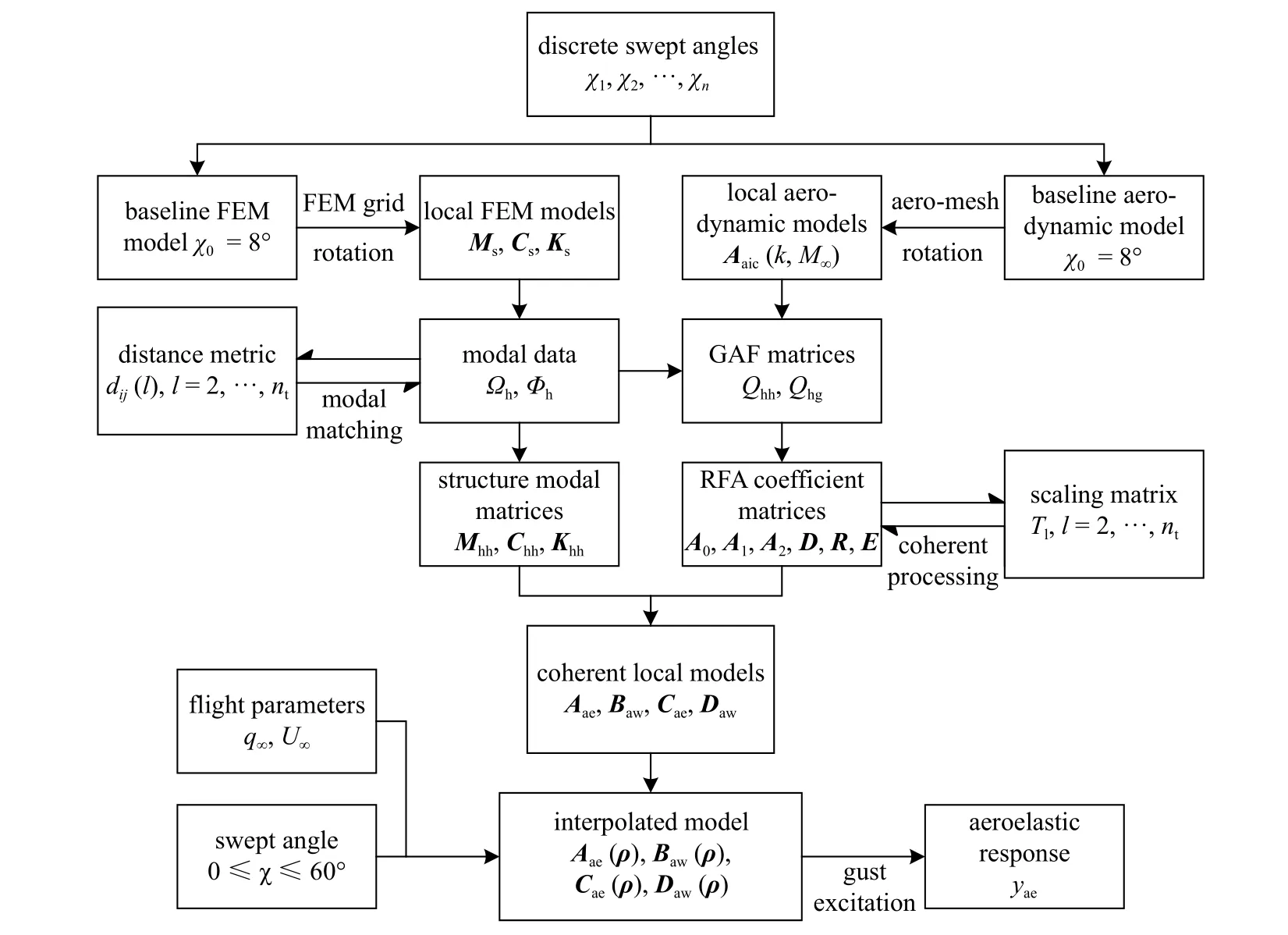
图5 变后掠翼的参数化气动弹性系统建模流程图Fig.5 The flow chat of the parameter-varying aeroelastic modeling for a variable-sweep wing

4 参变气动弹性建模方法的验证

4.1 一致性验证

为了利用当地建模技术建立变后掠翼的参变气动弹性模型，首先在0°～ 60°的后掠角范围内每间隔5°选取13 个离散的后掠角参数点，在这些参数点上分别建立当地气动弹性模型.初始的气动弹性模型包含式(4)中的结构矩阵和GAF 矩阵，由于不同后掠角之间的结构模态可能不匹配，因此原始当地系统的一致性无法保证.根据本文一致性处理方法，选取前6 阶结构模态，随后按照3.1 节给出的算法进行结构模态匹配.

图6 给出了经过模态匹配与排序后，变后掠翼的前6 阶固有频率随后掠角的变化规律.可以看出，在 55°～ 60 °后掠角之间，第5 阶和第6 阶结构模态发生了交叉现象.模态匹配过程中，这两个角度之间的具体MAC 数值如图7 所示，图中清晰地显示出在 60°下的第5 阶和第6 阶模态应与 55 °下的第6 阶和第5 阶模态相匹配.模态匹配算法给出了正确的匹配结果，确保每一个模态分支都随参数连续变化.

图6 前6 阶固有频率随后掠角的变化规律Fig.6 The first six natural frequencies vs.the swept angles

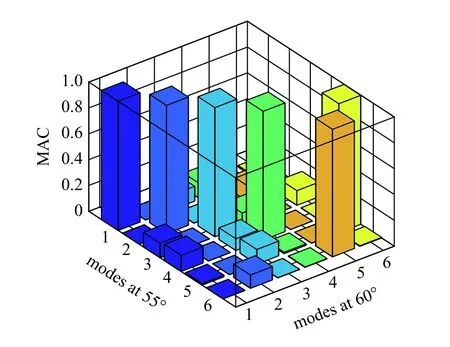
图7 MAC 值(55°和60°后掠角)Fig.7 The MAC values for 55° and 60° swept angles

为了建立时域状态空间模型，接下来对式(4)中的GAF 矩阵进行有理函数拟合.假设来流为不可压流动，GAF 矩阵在0.0～ 1.5 范围内的16 个减缩频率处计算.使用MS 方法拟合得到式(13)所示的RFA表达式，气动力滞后根由以下经验公式[32]得到

式中，kmax为减缩频率的最大值.

生成GAF 矩阵时使用了相匹配的结构模态，然而MS 算法并不保证各参数点下的RFA 系数矩阵具有一致性.如图8 所示，初始的RFA 系数矩阵D和E在参数变化时数值的跳跃现象非常显著.计算结果显示离散参数点处的RFA 拟合结果是具有足够精度的，然而跳跃的数值变化使参数点之间的插值无法进行.按照3.2 节给出的方法将系数矩阵处理为一致的形式后得到的结果如图9 所示.可以看出，处理后的系数矩阵D和E随着后掠角平滑、连续变化，具有一致性.需要强调的是，本文给出的处理方法不改变RFA 拟合结果，然而能够将RFA 表达式转化成为适合插值的形式.

图8 不一致的RFA 系数矩阵随后掠角的变化Fig.8 The incoherent RFA coefficients vs.the swept angles

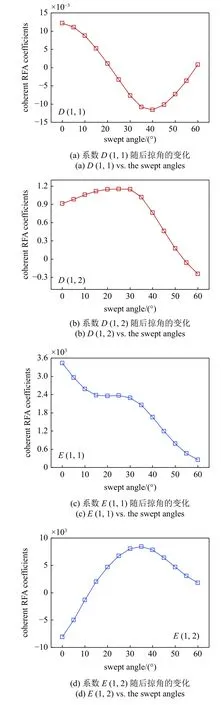
图9 一致性处理后RFA 系数矩阵随后掠角的变化Fig.9 The coherent RFA coefficients vs.the swept angles

匹配的结构模态和一致的RFA 表达式确保在构建状态空间模型时，各当地系统矩阵能够随参数连续变化，因此整个参数空间内任意点处的时域方程都能通过对当地系统模型的插值得到.为了验证插值模型的准确性，对后掠翼在突风扰动下的气动弹性响应进行计算.1-cos 离散突风是工程中常用的标准模型，当飞行器以速度U∞穿过突风场，突风参考点处受到的垂直扰动速度为

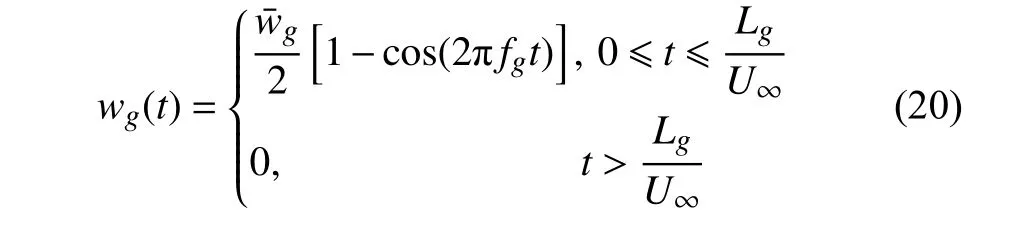
式中，为设计突风速度幅值，Lg为突风尺度，fg=U∞/Lg为突风激励频率.

在海平面大气环境下，来流速度为 120 m/s，1-cos突风频率为 3Hz，突风速度幅值为5 m/s.图10 和图11分别给出了后掠角为 28°和 48 °时后掠翼的时域动态响应，图中展示了翼梢加速度和翼根弯矩的计算结果. 28°后掠角下的系统模型通过对 25°和 30 °的当地模型线性插值得到，48°的模型通过对 45°和 50 °的当地模型插值得到，图中一并给出了各后掠角下精确的建模结果作为对比.结果显示，由一致系统矩阵得到的插值模型与精确模型计算出的结果相同，验证了对一致当地模型进行插值的方法是准确可靠的，而根据不一致系统矩阵建立的插值模型误差很大，动态响应与精确结果相比相去甚远.在 48 °时，不一致模型的响应是发散的，插值得到了不稳定的气动弹性模型.

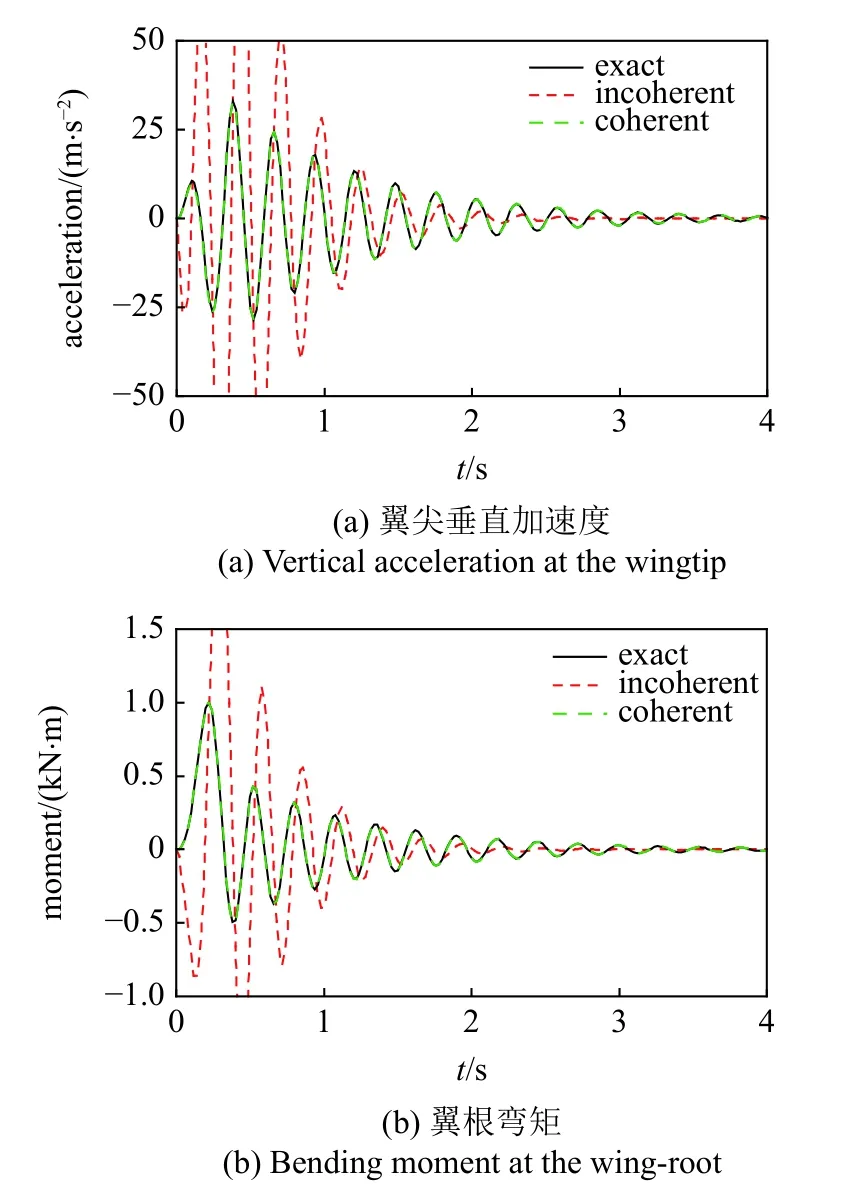
图10 后掠翼的1-cos 离散突风响应(χ=28°)Fig.10 1-cos gust response of wing at the swept angleχ=28°

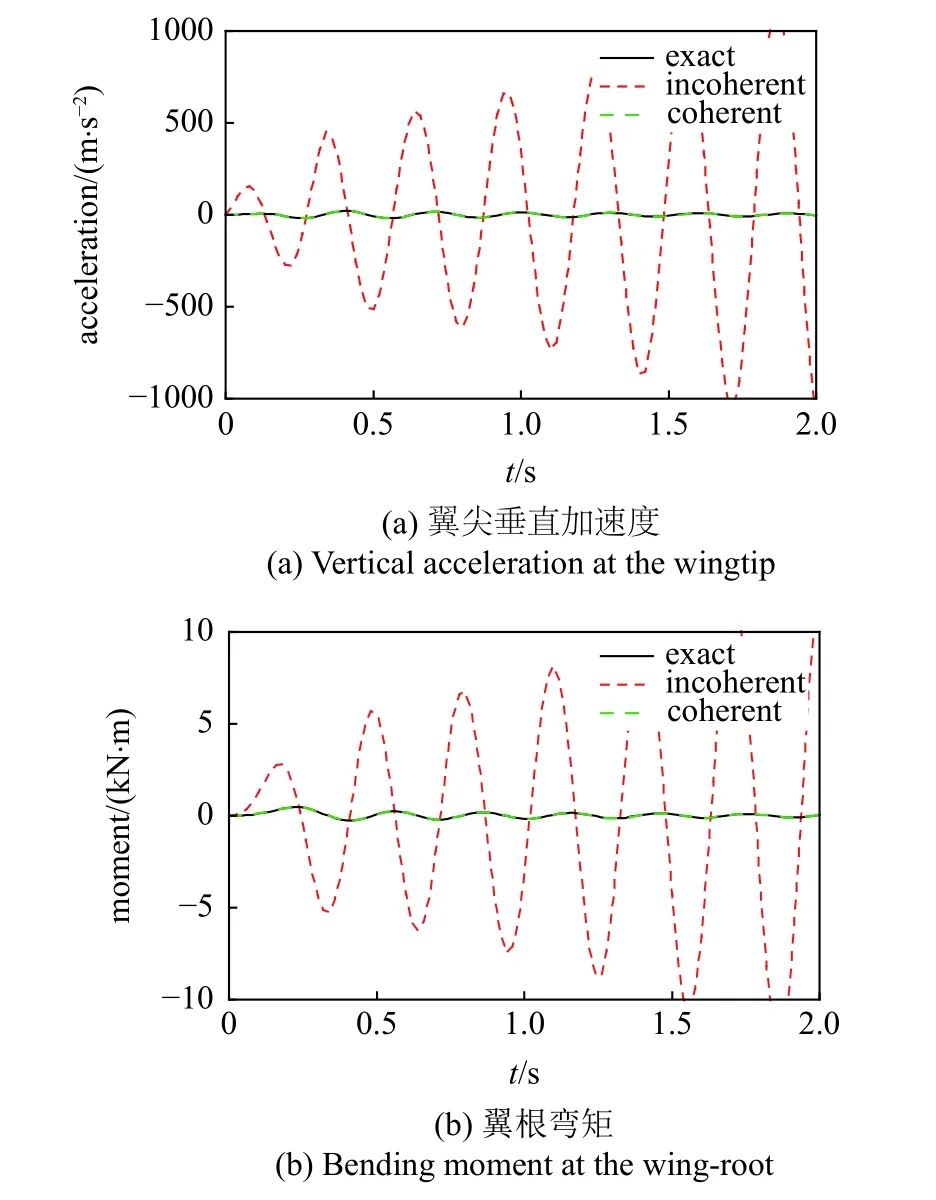
图11 后掠翼的1-cos 离散突风响应(χ=48°)Fig.11 1-cos gust response of wing at the swept angleχ=48°

4.2 颤振分析

图12 给出了固定马赫数、不同后掠角下的颤振速度分布，随着后掠角的增加，机翼的颤振速度不断增加.当机翼后掠角大于 18 °时，机翼颤振速度迅速增加，而当后掠角超过21°时颤振速度增加减缓.颤振速度在20°和21°之间发生了跳跃现象.利用p-k法，计算了机翼在20°和21°后掠角下的颤振特性，如图13 所示.发现当后掠角为20°时，随着来流速度的增加，第4 阶模态分支率先达到零点，系统发生颤振;而当后掠角增加到21°时，第1 阶模态分支首先穿越零点，失稳模态转为第1 阶模态.失稳模态的转换导致了颤振速度的跳跃现象.

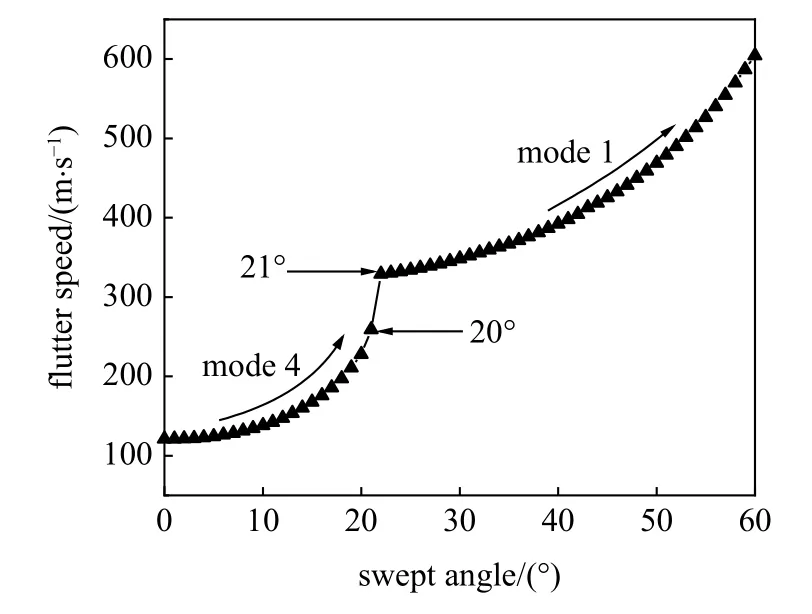
图12 可变后掠翼颤振速度随后掠角的变化Fig.12 Flutter speed vs.swept angle

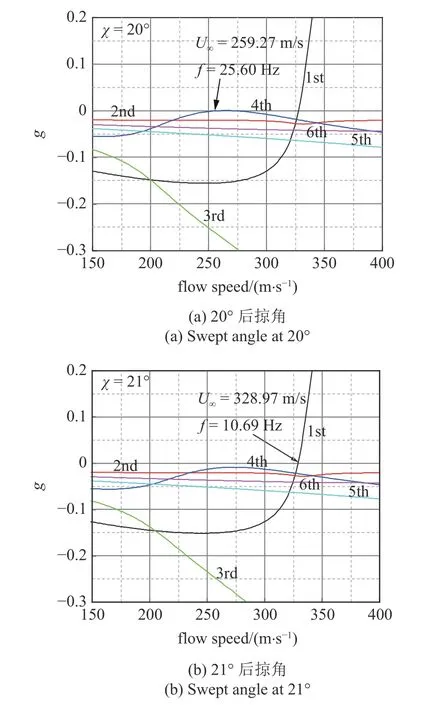
图13 不同后掠角下机翼的颤振分析Fig.13 Flutter analyses of the wing at different swept angle

为研究不同后掠角下系统特征值的变化规律，进行了固定马赫数(M∞=0.6)和来流速度(U∞=200 m/s)下不同后掠角处气动弹性系统的根轨迹分析，如图14 所示，图中箭头的方向是后掠角增加的方向.随着后掠角的增加，系统由失稳状态逐渐演变为稳定状态，这是结构和气动相互耦合作用的结果.由图6可以看出，当机翼的后掠角小于20°时，结构的第3 阶模态(第二阶弯曲模态)与第4 阶模态(第一阶扭转模态)的振动频率比较接近，容易诱发颤振.事实上，从图14 不同后掠角下气动弹性系统的根轨迹中也能看出，当后掠角小于18°时，系统失稳均发生在第4 阶模态处，而当后掠角较大时，结构的第3 阶与第4 阶固有频率相距较远，机翼不容易发生颤振.

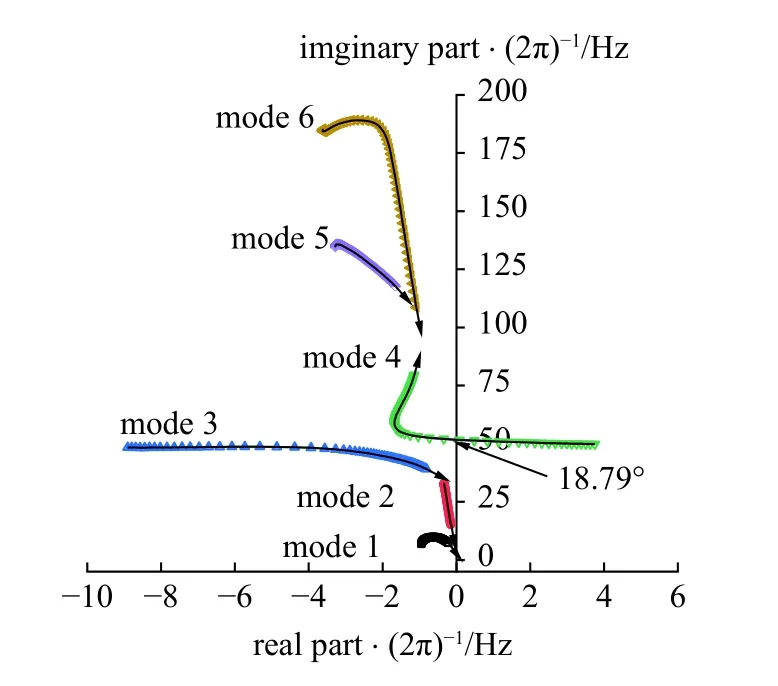
图14 可变后掠翼在不同后掠角下的根轨迹Fig.14 Root locus of the wing at various swept angles

4.3 时域仿真

为进一步分析可变后掠翼在变后掠过程中的时变动态特性，假定机翼后掠角的变化遵循如下规律

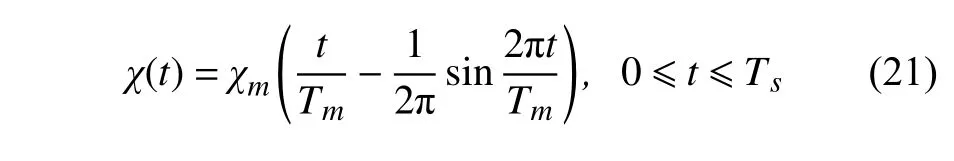
式中，χm=60°为最大后掠角，Tm=12 s 为从初始状态到最大后掠角所需要的总时间.

以Dryden 连续突风作为扰动激励，图15 给出了飞行马赫数为0.35，巡航速度为120 m/s 时，机翼连续改变后掠角过程中翼尖加速度和翼根弯矩的时间历程，其中连续突风尺度Lw=267 m，均方根值σw=2 m/s.

图15 机翼变后掠过程中的突风响应Fig.15 Gust responses of the variable-sweep wing during the morphing process

由图12 可以看出可变后掠翼的最小颤振速度发生在后掠角为 0 °时，其值为123.95 m/s.图15 可以看出，机翼以120 m/s 巡航速度飞行时，其速度已接近颤振速度，整个气动弹性系统的阻尼水平很低，所以开始遇到突风时，结构响应较大，但随着后掠角的不断增加，系统的阻尼水平增加，翼尖加速度与翼根弯矩响应变减弱.

选取了飞行马赫数为0.35 以及130 m/s 的巡航速度来研究变后掠翼变形过程中的时变气动弹性响应.如图16 所示.当后掠角小于8.27°时机翼处于气动弹性失稳状态，在一个较小的扰动下结构便发生了谐振荡，且不断从来流中获取能量导致振幅不断变大;而当后掠角大于8.27°时机翼结构的颤振速度增加，稳定性得到提升，结构进入气动弹性稳定状态，振幅不断下降.

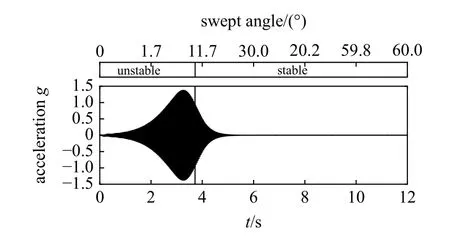
图16 后掠翼变形过程中的气动弹性响应Fig.16 Aeroelastic responses of the variable-sweep wing during the morphing process

5 结论

本文针对可变后掠翼，提出了一种参变气动弹性建模的实用方法.通过研究分析，可以得到如下结论.

(1)变后掠翼的气动弹性建模问题涉及参变系统的建模技术.对已获得的参变空间内的若干当地气动弹性模型进行插值，是参变气动弹性系统建模的高效而实用的方法.

(2)同一系统的状态空间实现是不唯一的，这导致各当地气动弹性模型可能存在不一致性，直接对这些不一致的当地气动弹性模型插值，将得到新参数点下错误的气动弹性模型.因此，对当地模型进行一致性处理至关重要.

(3)当地气动弹性模型的不一致性来源于结构和气动两方面.本文首先利用模态跟踪技术对结构模态进行匹配和对齐，解决了结构动力学方面的不一致性问题;在气动方面，在一致的结构模态基础之上建立非定常空气动力矩阵，然后对RFA 表达式中的系数矩阵进行合理的缩放处理，解决了空气动力系数矩阵的不一致问题.这样，最终的当地状态空间气动弹模型便具有良好的一致性，任意参数下的气动弹性模型可通过当地模型的插值快速获得，大大提高了系统稳定性分析和慢时变响应计算的效率.

(4)本文研究为采用频域气动模型的参变系统的气动弹性建模，提供了一种有效的解决方案.本文方法不仅使适用于变后掠情形，也适用于其他变体方式，具有一定的普适性.

(5)慢时仿真结果表明，机翼在变后掠过程中，其气动弹性稳定性和响应特性均发生很大变化，这些变化规律对变后掠翼飞行器的设计具有重要意义.