线形-拱形组合梁式三稳态压电俘能器动力学特性研究1)

张旭辉 陈路阳 陈孝玉 徐冬梅，† 朱福林 郭 岩

*(西安科技大学机械工程学院，西安 710054)

† (陕西省矿山机电装备智能监测重点实验室，西安 710054)

引言

无线监测技术在设备监测和安全监测等领域的应用越来越广泛[1-3]，但无线监测系统的续航问题一直制约其发展，化学电池供电存在维护成本高、环境污染和寿命有限等问题[4].振动能量俘获技术可以将环境振动能收集并转换为电能，有望实现无线监测系统自供电[5-8].

压电悬臂梁俘能器具有结构简单、尺寸紧凑等优点，国内外学者对此开展了大量的研究工作[9-12].经典的线性压电俘能器只能在其共振频率附近有效工作，当环境激励频率远离俘能器共振频率时，俘能器可俘获的能量显著减少，这一问题严重制约俘能器的实际应用[13].为提升俘能器俘能性能，研究人员提出了各种拓频方法，根据不同原理，可分为线性拓频和非线性拓频[14]，线性拓频方式主要包括:多悬臂梁阵列[15]、L 型梁[16]、多自由度梁[17].尽管上述结构能够有效拓宽俘能频带，但就其结构中单一悬臂梁而言，其工作频带宽度仍然很窄，系统结构尺寸较大，单位体积的俘能效率并不高.非线性拓频方式主要有:加装弹簧[18]、限制振幅[19]和磁场耦合[20]等方法，非线性方法能够拓宽单一悬臂梁的工作带宽，在各种非线性拓频方法中，引入非线性磁力的俘能器结构较为简单，在磁力作用下，俘能器能够在双稳态、三稳态甚至更多稳态下运行[21-23].为比较三稳态压俘能器和双稳态压电俘能器的性能，Zhou 等[24]对比分析了两种压电俘能器的频域响应特性.Zhu 等[25]分析了随机激励下两种压电俘能器的输出性能，研究结果均表明:三稳态压电俘能器具有更浅的势阱，更宽的俘能频带以及较高的输出.Leng 等[26]的研究表明:三稳态压电俘能器在低强度和较高强度下的最佳磁距较为接近，意味着最佳磁距下的俘能器能够有效适应激励强度的变化.Jung 等[27]设计了一种外部磁铁可旋转的三稳态压电俘能器，研究表明，调整外部磁铁旋转至合适倾角能够有效提高输出性能.Wang 等[28]在考虑悬臂梁几何非线性(GNL)和引力效应(GE)的基础上，建立分布式参数模型，研究表明:较低激励下，具有GNL 和GE 的三稳态压电俘能器具有非对称势阱，能够提升俘能器输出性能.Cao 等[29]分析了几何参数对三稳态压电俘能器势阱深度的影响，较浅的势阱能够有效拓宽工作频带并且提升低频环境下的俘能性能.由于环境中的激励具有多方向的特点，采用直梁结构的压电俘能器难以在多方向激励环境中实际应用.Chen 等[30]通过仿真发现引入拱形结构的压电悬臂梁应变分布更加均匀，有利于提高能量转换效率和电压输出.Zhao 等[31]设计了一种弧形梁俘能器，COMSOL 仿真表明弧形梁能够响应来自不同方向的激励.针对曲梁的研究[32-33]表明:采用曲梁结构的俘能器有着良好的输出性能，且曲梁可拉伸变形，有望实现多方向的能量俘获.

引入非线性磁场的压电俘能器结构简单，较传统线性结构有着更宽的工作频带.本文针对煤矿井下无线监测节点供电需求，为适应采掘激励低频、多方向等特点，引入拱形结构，设计一种线形-拱形组合梁式三稳态压电俘能器，建立线形-拱形组合梁式压电俘能器动力学模型，借助数值仿真从时域角度分析了俘能器磁铁水平间距、垂直间距和激励加速度对动力学响应特性的影响规律，并搭建实验平台，验证理论分析的正确性，研究可为线形-拱形组合梁式三稳态压电俘能器的优化设计提供理论指导.

1 三稳态压电俘能器结构

如图1 为线形-拱形组合梁式三稳态压电俘能器结构示意图，结构由线形-拱形组合梁、柔性压电材料PVDF 和磁铁A，B，C 组成.线形-拱形组合梁上黏贴PVDF，外接负载电阻R，磁铁A 固定于组合梁末端，磁铁B，C 对称布置于X轴两侧，磁铁A 与磁铁B，C 间水平距离为d，磁铁B，C 的垂直间距为2dg.图中组合梁在X轴方向长度为L，组合梁宽度为b，厚度hS，线形部分长度L1，拱形部分半径和弦长分别为r和 2r，黏贴在组合梁上的PVDF宽度与组合梁一致，厚度为hp，w(L，t) 为悬臂梁末端在t时刻的振动位移.

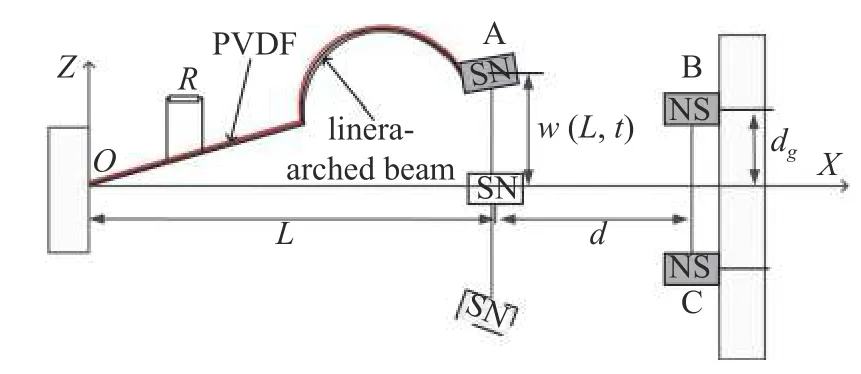
图1 线形-拱形组合梁式三稳态压电俘能器结构示意图Fig.1 Schematic diagram of linear-arch beam TPEH

2 三稳态压电俘能器动力学模型

2.1 非线性磁力建模

为准确分析压电悬臂梁振动特性，需要确定其末端受到的非线性磁力大小，磁铁A，B，C 间的几何关系如图2 所示，本文采用磁偶极子模型描述非线性磁力，磁铁B 在磁铁A 处产生的磁通密度为[34]

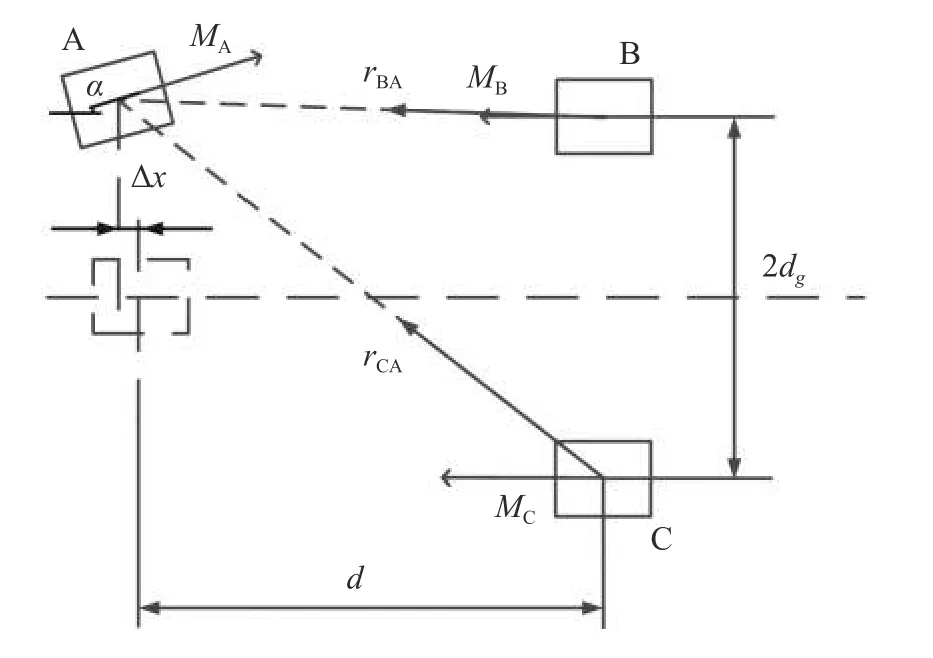
图2 非线性磁力模型Fig.2 Nonlinear magnetic force model

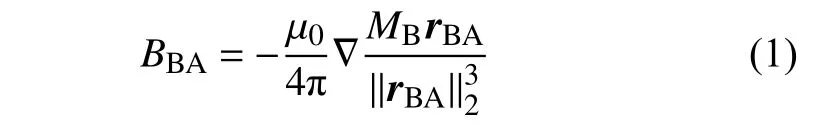
式中，μ0为真空磁导率，∇为向量梯度，rBA为磁铁B 到A 的方向向量，MB为磁偶极子B 的磁矩.

磁铁B 在磁铁A 处产生的势能为

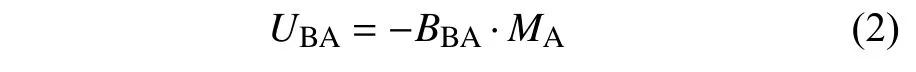
式中，MA为磁偶极子A 的磁矩.

Δx为磁铁A 的水平位移，由于磁铁尺寸相较于组合梁尺寸小，所以 Δx≈0，有lasinα ≪w(L，t)，α=arctanw′(L，t)，可得[35-36]

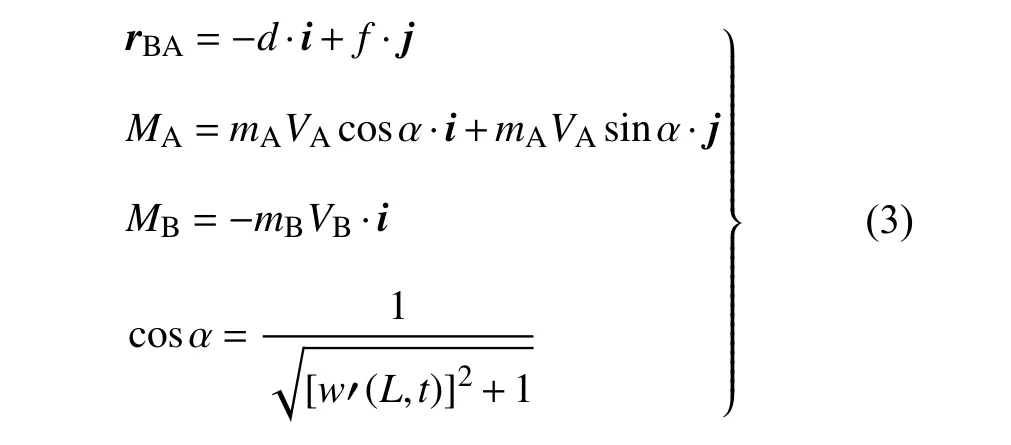
式中，分别i和j为X和Z轴方向的单位向量，mA和mB分别表示磁铁A，B 的磁化强度，VA和VB表示磁铁A，B 的体积.将式(1) 和式(3) 代入式(2) 可得

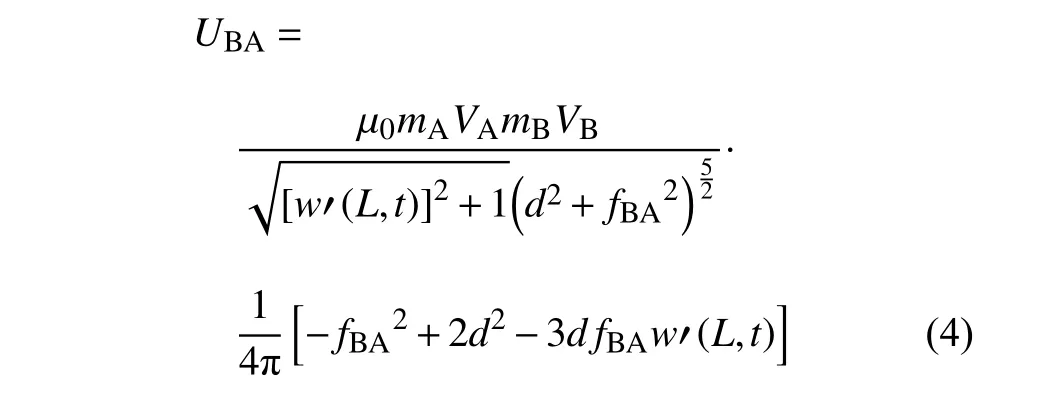
式中，fBA=w(L，t)-dg.

同理，磁铁C 在磁铁A 处产生的势能

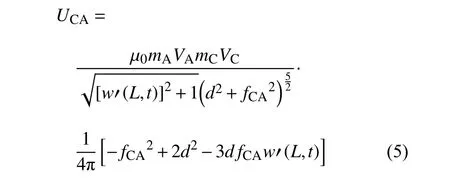
式中，fCA=w(L，t)+dg.

磁铁B，C 在组合梁末端磁铁A 处产生的总势能

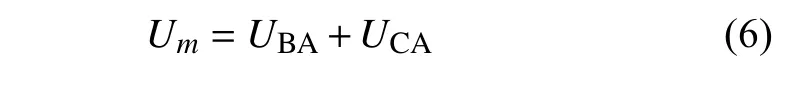
因此磁铁A 受到的非线性磁力

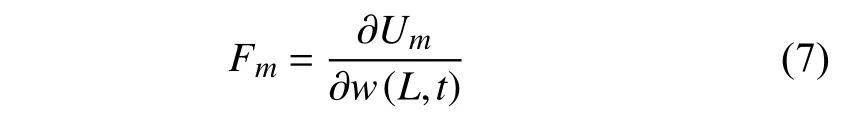
2.2 线形-拱形组合梁恢复力

采用YLK-10 测力计测量线形-拱形组合梁在Z轴方向的恢复力大小，多次测量取平均值.如图3所示为组合梁非线性恢复力的实验测量和拟合结果，采用多项式拟合得到恢复力的表达式

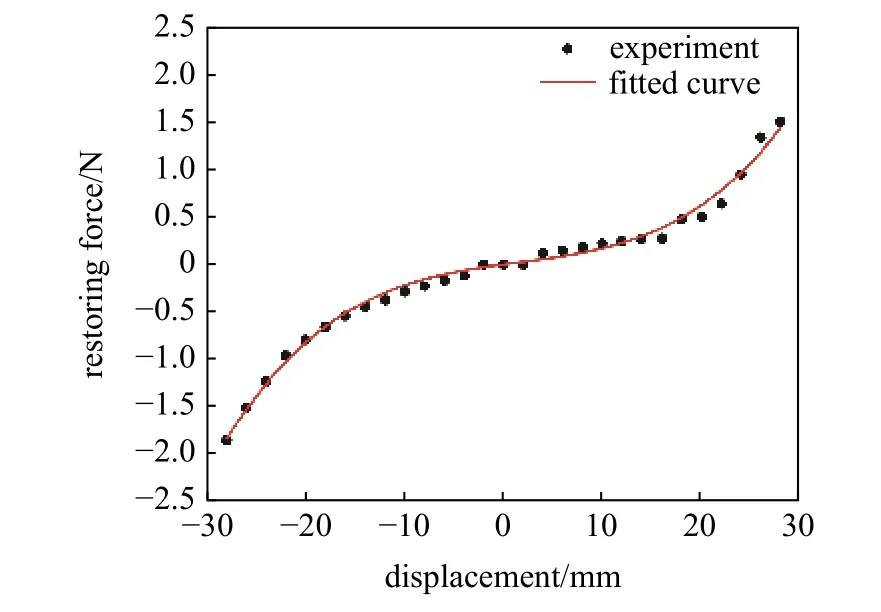
图3 线形-拱形组合梁位移-恢复力曲线图Fig.3 Nonlinear restoring force of linear-arch beam

式中，w(L，t) 是组合梁末端在t时刻沿Z轴的位移.

从图3 中可以看出，线形-拱形组合梁不同于传统的直梁，其恢复力具有非线性，以w(L，t)=0 为悬臂梁的平衡位置，组合梁在平衡位置两侧的恢复力大小并不相等，这是由于拱形部分的存在，其曲率变小时恢复力比曲率变大时要小.

2.3 压电俘能器动力学方程

为确定组合梁的振动位移w(x，t).使用Rayleigh-Ritz 法将组合梁的振动位移展开

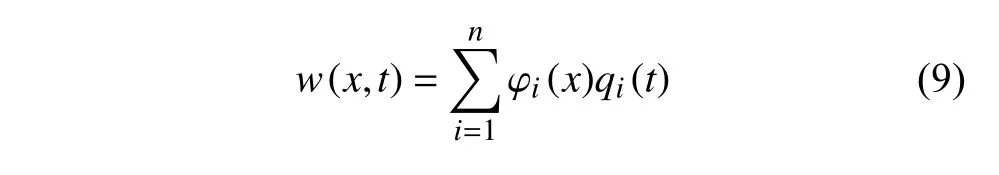
其中，i为组合梁的振动模态阶数，φi(x) 表示组合梁的第i阶模态函数，qi(t)表示第i个广义模态坐标.

由于环境中的激励以低频为主，组合梁的一阶模态弯曲振动起主导作用，因此本文仅考虑组合梁的一阶模态.对于线形-拱形组合梁，由于结构复杂，难以获取模态函数解析表达式，由于其一端夹紧固定于基座之上，另一端自由，使用容许函数表示模态函数[37]

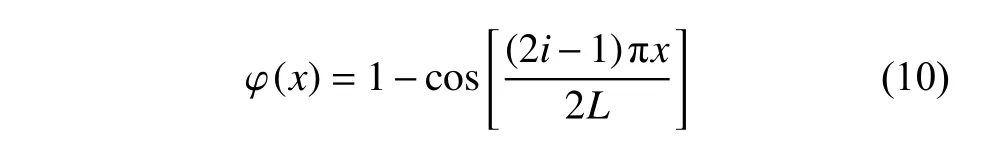
采用拉格朗日方程建立线形-拱形组合梁的运动方程

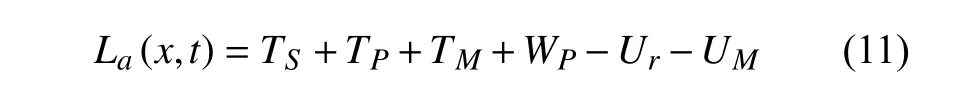
式中，TS，TP，TM分别为金属基层、压电层和末端磁铁的动能，WP为PVDF 的电能，Ur为线形-拱形组合梁压电悬臂梁势能，UM为组合梁末端磁铁与外部磁铁之间作用力产生的势能.

金属基层和压电层的动能和组合梁的势能可表示为

式中，“·”为表示t求导，ρS为金属基层的密度，AS为金属基层的横截面积，ρP为压电层的密度，AP为压电层的横截面积，z(t) 为基座振动位移.

组合梁末端磁铁的动能为

式中Mt为磁铁的质量，It为磁铁的转动惯量.

压电层在Z方向的电场强度E3和电位移D3可由压电材料的本构方程给出

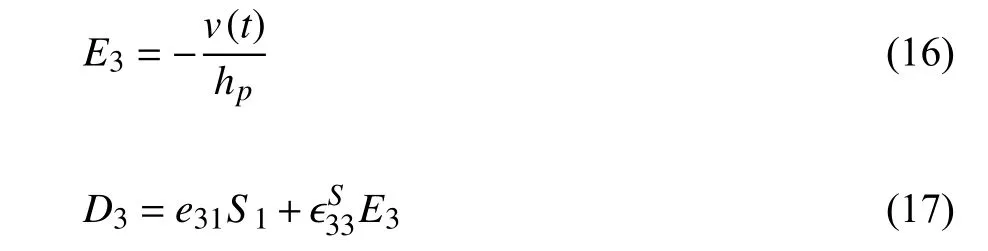
当组合梁受激振动形变，金属基层上的PVDF随之形变，由压电效应产生电能

结合非线性磁力、恢复力的分析，根据欧拉-伯努利梁理论和基尔霍夫定律可得线形-拱形组合梁的系统动力学方程

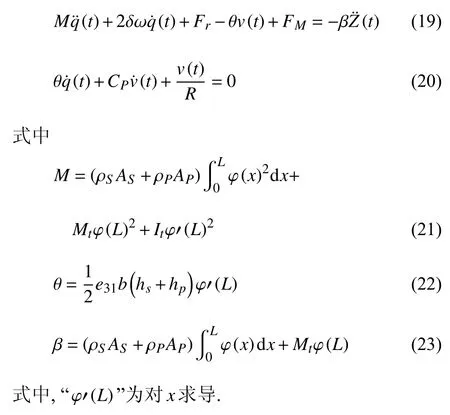
3 三稳态压电俘能器动力学分析

3.1 势能和磁力分析

表1 给出了三稳态压电俘能器中组合梁和磁铁的结构、材料参数.

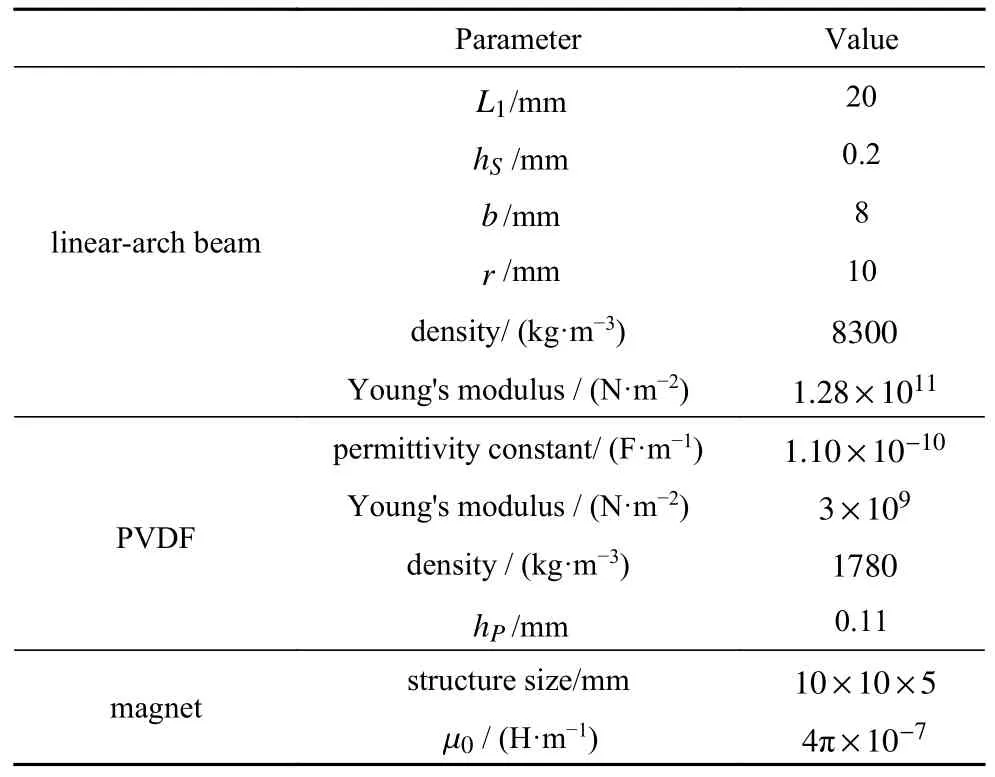
表1 三稳态压电俘能器结构和材料参数Table 1 Structure and material parameters of TPEH

系统总势能为

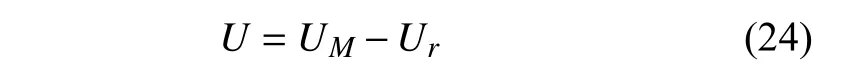
由式(24)可知，水平磁距d和垂直磁距dg对系统势能和磁力起决定性的影响，本节将通过仿真分析上述参数对系统势能和磁力的影响.

图4 显示了d=16 mm，dg分别为0 mm，6 mm，8 mm，12 mm 和20 mm 时压电俘能器系统势能和磁力仿真结果.由图4(a)所示结果可知，保持d不变的情况下，随着dg的逐渐增大，系统势能曲线依次呈现双势阱、三势阱和单势阱.当dg=0 mm 时，外部磁铁B，C 重合在一起，系统势能曲线有两个势阱，此时俘能器为双稳态系统，但两个势阱的深度和宽度都较大，低激励下系统难以克服势垒的阻碍实现双稳态运动.当dg增至6 mm，系统势能曲线的两个势阱深度变浅，宽度变窄，低激励下的俘能器能够实现双稳态运动.随着dg的增大，系统势能曲线由两个势阱向3 个势阱转变，系统中间势阱深度逐渐变深，宽度增加，两侧势阱深度逐渐变浅，宽度减小.从图4(b)可以看出，随着dg的增大磁力逐渐减小，组合梁摆脱磁力约束所需的能量也越少.

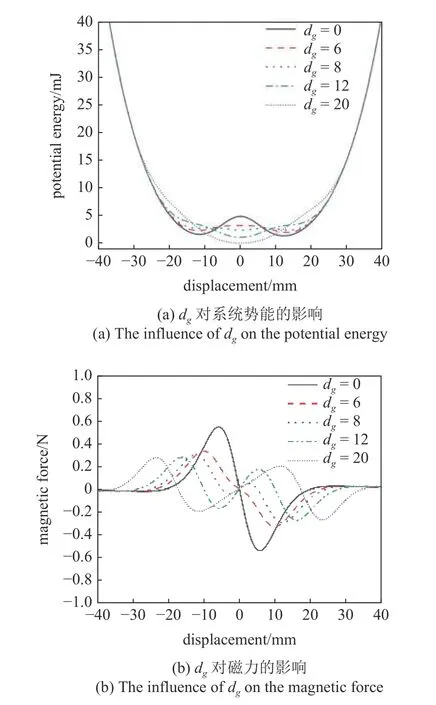
图4 dg 对系统势能和磁力的影响Fig.4 The influence of dg on potential energy and magnetic force

图5 显示了dg=0 mm，d分别为0 mm，10 mm，13 mm，15 mm 和22 mm 时压电俘能器系统势能和磁力仿真结果，如图5(a)所示:随着d的逐渐减小，系统势能曲线由单势阱变为三势阱，势阱深度随着d的减小逐渐增大.d=0 mm 时，势能曲线的3 个势阱较深，只有当外部激励较大时，才能够使系统在阱间运动，实现三稳态运动.由图5(b)所示结果可知，随着d的逐渐减小，组合梁末端磁铁与外部两磁铁间作用力逐渐变大，磁铁间作用力增强，组合梁摆脱磁力约束所需的激励越大.从图6(a)和5(a)中可以看出，当势能曲线出现3 个势阱时，位于外侧的两个势阱深度不同，这是由于组合梁恢复力不对称导致的非对称势阱.

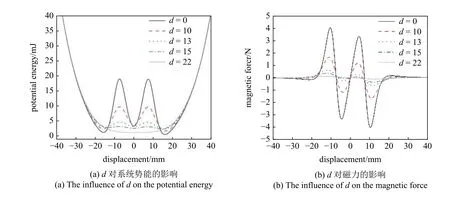
图5 d 对系统势能和磁力的影响Fig.5 The influence of d on potential energy and magnetic force

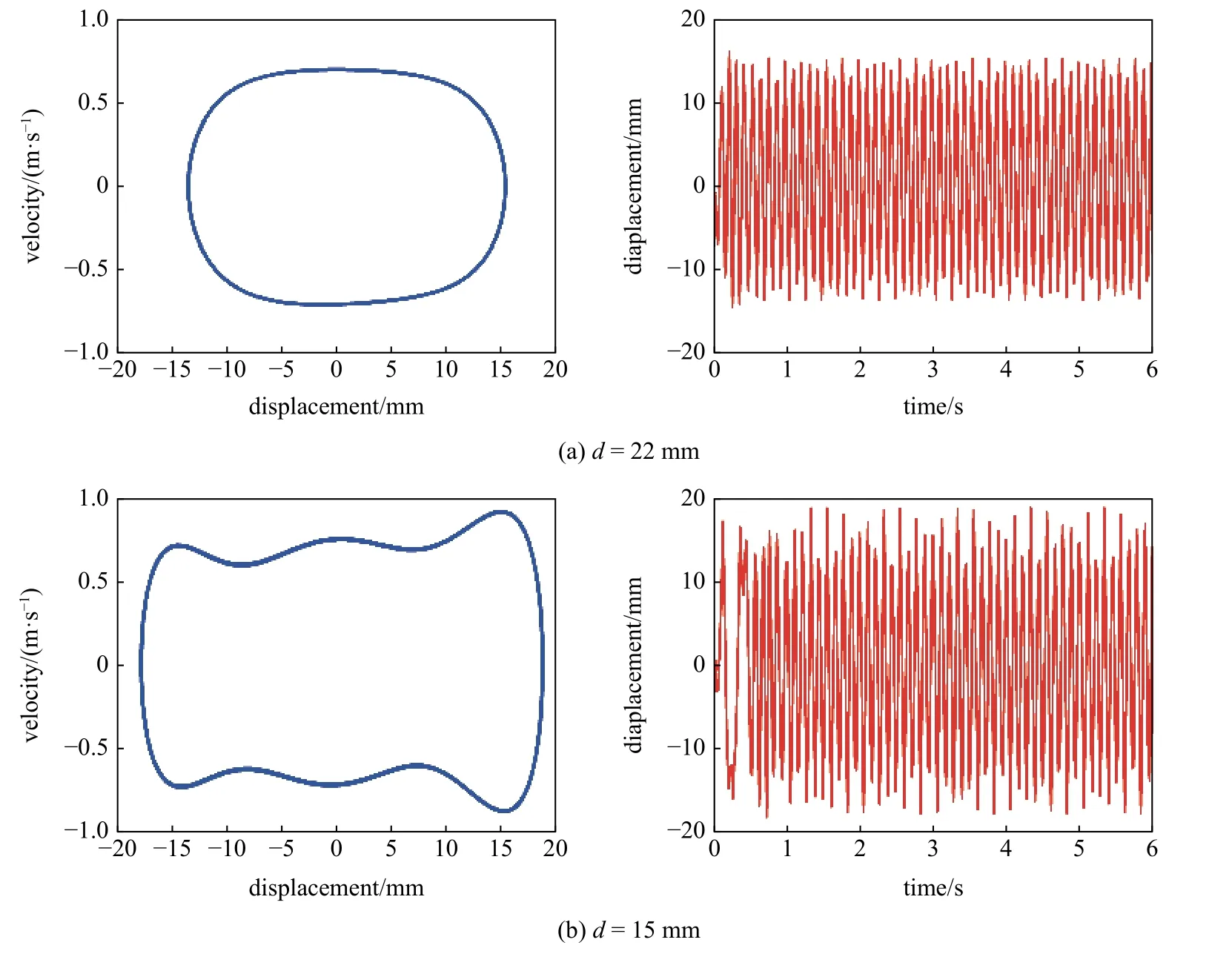
图6 不同水平间距 d 下的系统相图和时间-位移图Fig.6 Phase portrait and time-displacement diagram of different magnetic distanced

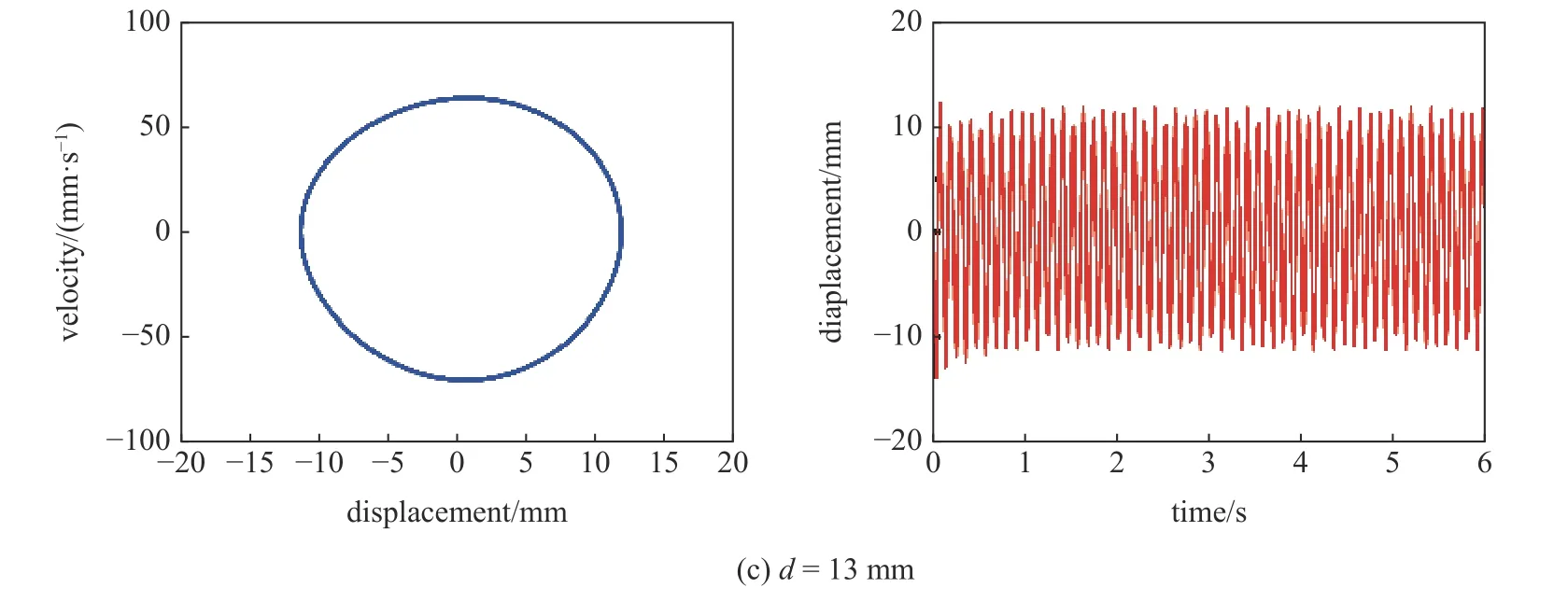
图6 不同水平间距 d 下的系统相图和时间-位移图(续)Fig.6 Phase portrait and time-displacement diagram of different magnetic distance d (continued)

3.2 系统动力学特性分析

系统势能和磁力分析结果表明:磁铁间距对系统势能和磁力有着显著影响，一定激励条件下，调整磁铁间距能够使系统实现不同的运动状态，当磁铁间距较小时，磁铁A 与磁铁B，C 间作用力较大，此时势阱较深，低水平的激励下，系统难以越过势垒，脱离势阱较深的位置.因此，合理的选择磁铁间距显得尤为重要，本节将对磁铁水平间距d、垂直间距dg和激励加速度a对系统动力学响应特性的影响规律进行探究.

3.2.1 水平间距d对系统动力学特性的影响

当a=12 m/s2，dg=8 mm，f=9 Hz，d分别为22 mm，15 mm，13 mm.如图6 所示为压电俘能器的位移-速度相图和时间-位移图.从图6(a)可以看出，当磁铁水平间距d=22 mm 时，由于此时磁力较小，磁力对组合梁几乎不产生约束作用，压电俘能器表现出单稳态运动特性.当水平间距d=15 mm，结合图5 可知，磁铁间作用力增大，磁力作用下系统出现3 个势阱，且势阱深度较浅，因此系统能够轻易越过势垒，如图6(b)所示，组合梁末端在3 个平衡位置之间往复运动，系统实现三稳态运动，组合梁的振动位移幅值大幅提高，达到18 mm.当d减小至13 mm，由于磁铁之间作用力较大，组合梁难以摆脱磁力束缚，如图6(c)所示，系统表现出单稳态特性，在中心平衡点附近作小幅值的周期运动，此时系统响应位移、振动速度和输出电压都非常小.

3.2.2 垂直间距dg对系统动力学特性的影响

取a=12 m/s2，d=16 mm，f=9 Hz，dg分别为6 mm，8 mm 和12 mm.压电俘能器的位移-速度相图和时间-位移图如图7 所示.通过调整磁铁垂直间距dg，系统具有不同的动力学特性，随着dg的增大，系统依次经历双稳态、三稳态和单稳态3 种运动状态.如图7(a)所示，当dg=6 mm，磁力作用下系统具有两个势阱，在给定激励下系统能够在阱间往复运动实现双稳态运动.当dg=8 mm，如图7(b)所示，系统作三稳态运动，在3 个稳定位置间往复运动，俘能器的响应位移和输出性能都较高.随着磁铁间距的增大，如图7(c)所示，磁铁作用力减小，系统表现出单稳态特征，组合梁末端仅在中间平衡点附近作小幅值的周期运动.

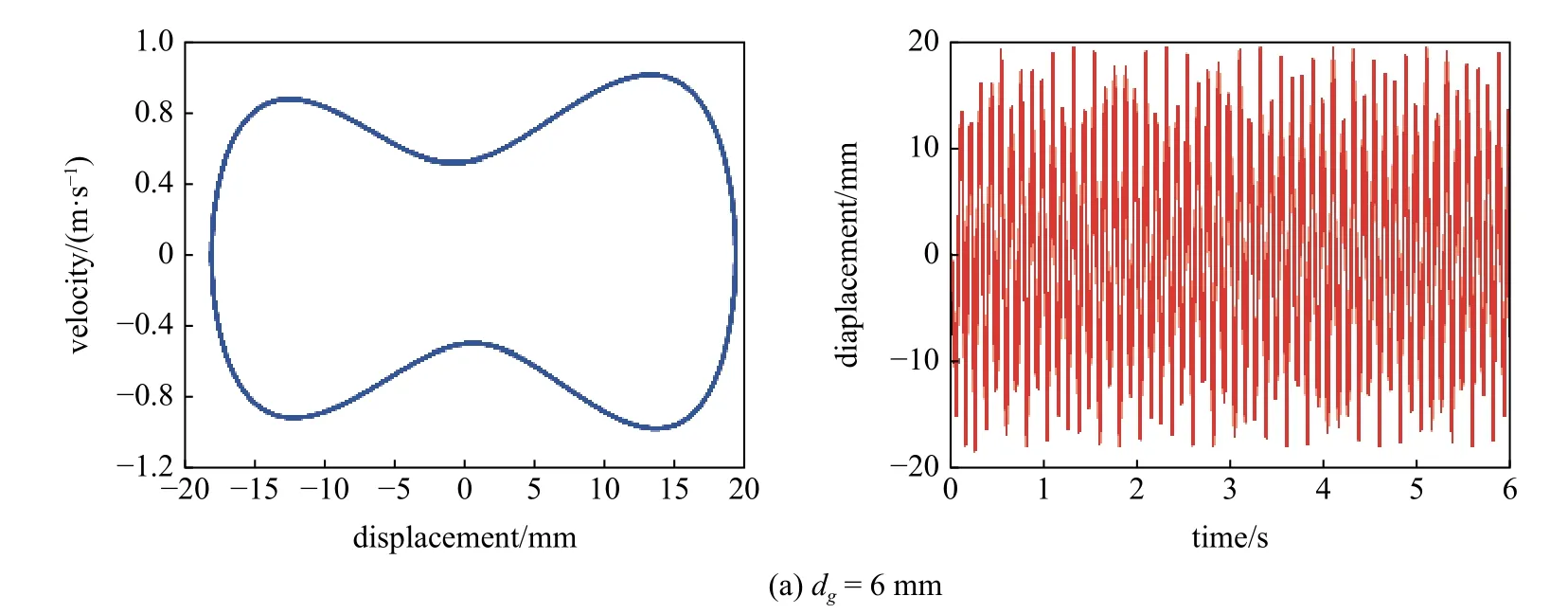
图7 不同垂直间距 dg 下的系统相图和时间-位移图Fig.7 Phase portrait and time-displacement diagram of different magnetic distance dg

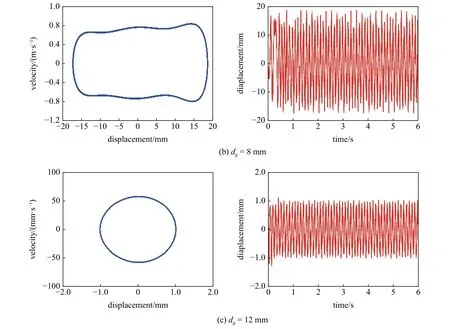
图7 不同垂直间距 dg 下的系统相图和时间-位移图(续)Fig.7 Phase portrait and time-displacement diagram of different magnetic distance dg (continued)

3.2.3 激励加速度a对系统动力学特性的影响

取d=15 mm，dg=8 mm，f=9 Hz，研究激励加速度a对系统动力学特性的影响规律.如图8 所示为5 m/s2，7 m/s2和12 m/s2的位移-速度相图和时间-位移图.当d=15 mm，dg=8 mm，系统势能曲线具有3 个势阱，但系统并不能在任意激励加速度下实现三稳态，当a=5 m/s2，系统不能越过势垒，只能在中间稳定位置附近作小幅周期运动.当a=7 m/s2，系统获得的动能增加，响应位移相较于a=5 m/s2时有所增大，但不足以使系统越过两侧的势阱，仍然在中间稳定位置附近作阱内运动.当加速度增大至a=12 m/s2，系统能够越过两侧的势垒，在3 个势阱间运动，实现三稳态运动，此时系统的响应位移和输出性能都将大幅提高.

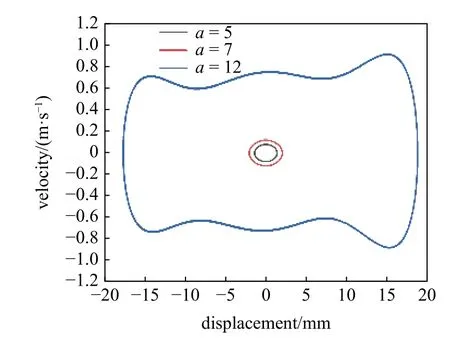
图8 不同激励加速度下的系统相图Fig.8 Phase portrait of different excitation acceleration

从图6～ 图8 可以看出，组合梁运动至两侧稳定位置时速度不相等，这是由于线形-拱形组合梁非线性恢复力的不对称性所致.

4 实验验证

为验证俘能器动力学特性理论分析的正确性，根据表1 所示结构参数制作压电俘能器样机并搭建实验平台进行实验验证，如图9 所示，实验平台由:计算机、振动控制器、功率放大器、振动台、激光测振仪、COCO80 采集仪、线形-拱形组合梁式三稳态压电俘能器及基座组成.实验中，通过计算机设置激励条件，由振动控制器发出激励信号，经由功率放大器输出至振动台，振动台按照预设的激励信号运行，使用激光测振仪实时测量组合梁拱形部分的响应速度.

图9 实验平台Fig.9 Experimental platform

图10 所示是d=15 mm，dg=8 mm，f=9 Hz，激励加速度分别为5 m/s2，7 m/s2和12 m/s2时的线形-拱形组合梁位移-速度的实验结果.如图10(a)和图10(b)所示，当a=5 m/s2时，位移幅值为1.8 mm，随着激励加速度的增大，位移幅值随之增大，当a=7 m/s2时，位移幅值为2.5 mm，表明在较低的激励下，系统无法越过两侧势垒，只能在阱内作周期运动.图10(c)是7 m/s2下的俘能器位移-速度相图，此时系统能够越过势垒，表现出三稳态运动特征.

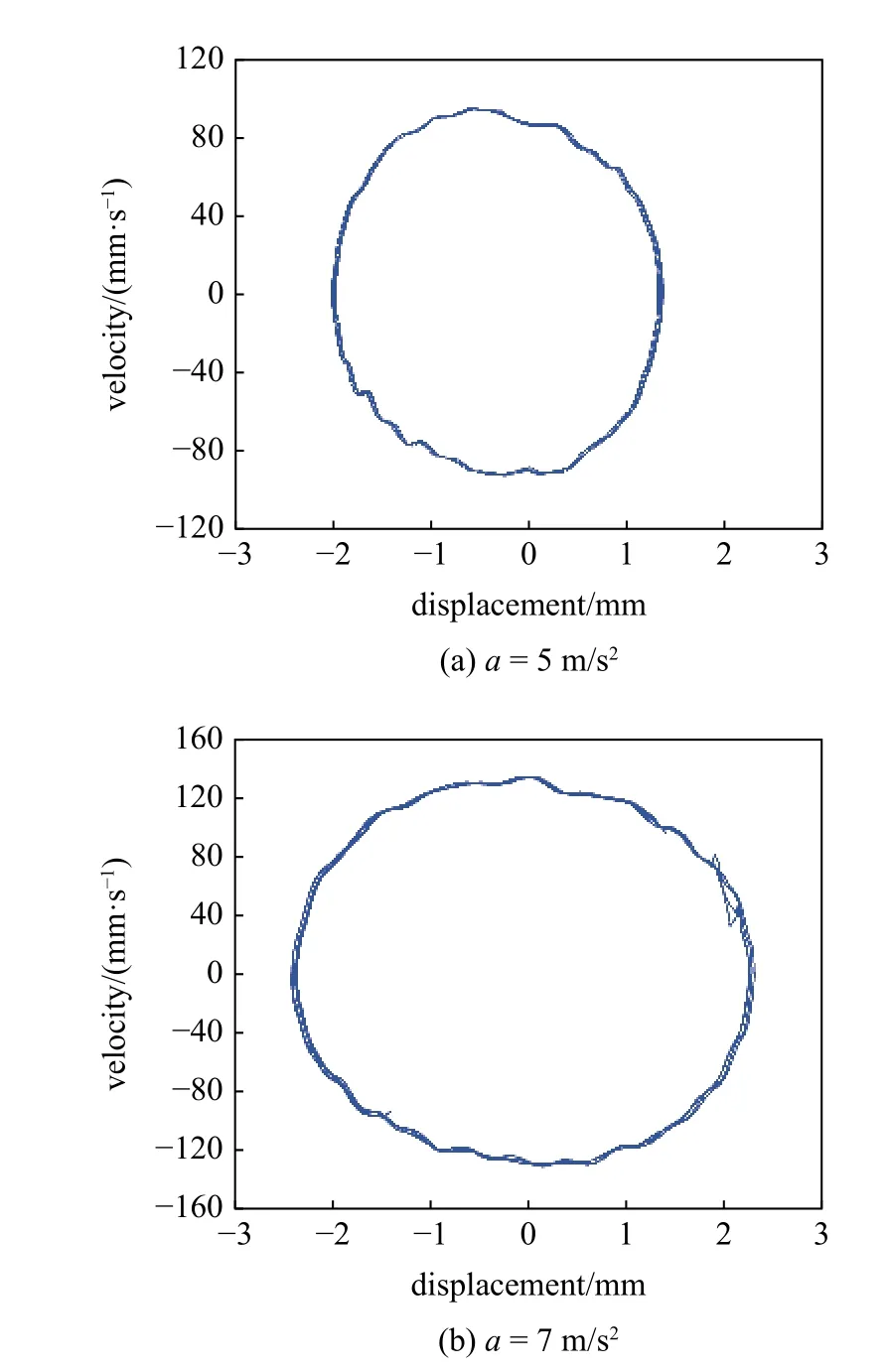
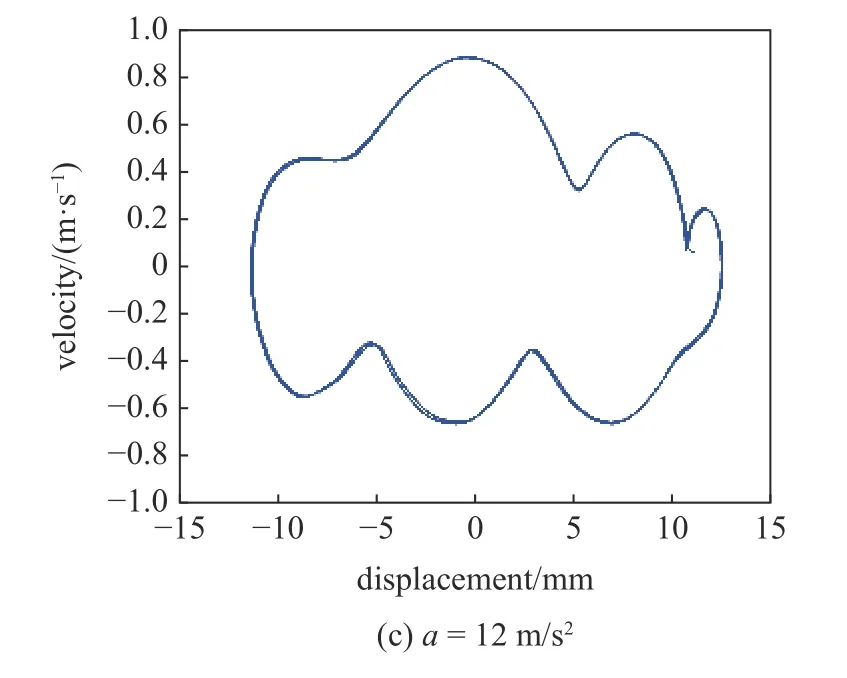
图10 不同激励加速度下的实验相图Fig.10 Experimental phase diagrams under different excitation accelerations

低激励下的实验结果与仿真结果较为吻合，但随着激励的增大，特别是当系统作三稳态运动时，由于组合梁形变较大，实验与仿真结果之间存在误差，其主要原因有:(1)线形-拱形组合梁压电俘能器样机制作产生的加工误差，造成实验条件与仿真存在偏差;(2)实验得到的相图倾斜明显，而仿真得到的相图倾斜并不明显，这是由于仿真中未考虑重力因素，且实验中由于拱形部分的存在，难以精准测量其形变位移，导致激光测振仪测量的数据存在偏差.

5 结论

本文针对线形-拱形组合梁式三稳态压电俘能器，基于拉格朗日方程建立了动力学模型，使用4 阶龙格-库塔算法对动力学方程进行数值求解，分析了不同磁距对系统特征，初步揭示了不同加速度对系统动力学性能的影响规律，通过实验验证了理论分析的正确性.仿真与实验得到以下主要结论.

(1)保持dg不变时，通过改变d，系统能够构成单稳态系统和三稳态系统.保持d不变时，增大dg，系统将依次构成双稳态、三稳态和单稳态系统.当系统作三稳态运动时，系统振动响应位移将明显提高，特别地，当d=16 mm，dg=8 mm，时，系统势能曲线有3 个势阱，且势阱深度较浅，宽度较为一致，这有利于系统在低激励下产生大幅响应，并提高俘能器输出性能.

(2)随着激励水平的增加，系统更易越过势垒实现阱间运动，俘能器响应位移随之增大.

(3)线形-拱形组合梁的非对称恢复力导致势能曲线呈现非对称势阱，这为低激励环境中的俘能器应用提供了新的解决思路.