非恒定流条件下长江干线叙泸段航道水位变化预测模型验证

张文 付旭辉 童庆 赵致哲 罗媛媛 黄岱

摘要：金沙江向家坝水电站运行以来，产生的非恒定流过程给长江上游宜宾—泸州段航道船舶通行造成了不利影响。为减少因水位变化引起的损失，并使船舶顺利通过航道沿程滩险， 提出了一维非恒定流数学模型，并计算出叙泸段航道沿程流量与水位过程。结果表明：计算误差可满足规范误差范围的要求，一维非恒定流程序准确率和可靠性得到了验证。研究成果可用于分析叙泸段航道的非恒定流沿程变化特征和沿程滩险受非恒定流影响下的航道要素变化规律。

关键词：叙泸段非恒定流;水位预测模型;四点迭代法;模型验证

中图法分类号：U617 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2021.12.015

文章编号：1006 - 0081（2021）12 - 0087 - 05

0 引 言

为使长江干线航运进一步蓬勃发展，需要对长江干线航道进行全面、系统的综合治理，提升航道通航能力，但由于长江上游宜宾-泸州段航道水流条件受上游干流向家坝枢纽和支流枢纽的下泄非恒定流影响，沿程滩险的航道要素变化剧烈，滩险水位预测困难，给枯水期的航道维护、管理和航道要素预测预报带来巨大困难。

长江上游宜宾-泸州段的电站在运行过程中产生的非恒定流，会改变坝下河段天然水流特征，对坝下游航道、港口等通航设施的正常使用及船舶航行带来重要影响，但查阅相关资料发现对于长江干流非恒定流影响航道的研究较少，因此，研究非恒定流对下游航道通航条件的影响，对船舶安全航行和作业具有重要作用。

为了降低长江上游宜宾-泸州段的非恒定流影响，本文根据实测数据，围绕重点滩险的航道尺度预报，通过数学模型，创新性地采用了四点迭代法，建立并验证了非恒定流条件下叙泸段航道水位变化预测模型。

1 研究背景

自2012年10月金沙江向家坝水电站蓄水运行以来，下泄的日调节非恒定流和岷江梯级枢纽下泄的日调节非恒定流在宜宾汇合后，产生新的非恒定流过程，日水位变幅达3.5 m，同枯水期航道水深相近[1]，向下游传递影响范围可至重庆江津，部分改善了航道条件，但也给长江上游黄金航道的航运带来诸多新问题，长江上游叙泸河段河势示意见图1。

目前，长江上游宜宾-泸州段航道水流条件受上游干流向家坝枢纽和支流犍为等枢纽下泄非恒定流影响，沿程滩险的航道要素变化剧烈，滩险水位预测困难，给枯水期的航道维护、管理和航道要素预测预报带来较大困难[2-3]，长江干线叙泸段航道滩险分布见图2。

在向家坝日调节非恒定流作用下的航道滩险航道要素变化规律复杂，导致叙泸河段航道卵石滩险航道尺度特征不易把握，给航道维护和信息预测发布带来困难[4-5]。因此，有必要对日调节非恒定流作用下叙泸段航道典型滩险航道要素的预测预报开展研究，通过研讨叙泸段航道的非恒定流沿程变化特征、对沿程滩险受非恒定流影响下的航道要素变化规律进行水位变化预测，可为该河段的航道维护、管理提供技术支撑，从而确保航道安全畅通。

本文旨在对叙泸段航道范围内的非恒定流在重点滩险航道尺度影响进行深入分析，研究日调节非恒定流波峰、波谷传递条件下航道尺度的变化特征，进行航道尺度短期预报，从而实现叙泸段重点滩险水位的中短期预报，预报精度基本满足规范的要求。

2 计算方法

非恒定流段传播特性的计算多采用特征线法、有限差分法和四点迭代求解法[6]，针对叙泸段的非恒定流计算，基于明渠非恒定流传播特性的研究成果，结合叙泸段航道的干支流交汇特点，以及复杂河床地形、滩险特征等水文、河床边界条件，建立适用于叙泸段航道尺度计算的一维非恒定流计算方法，采用四点迭代求解法进行求解。

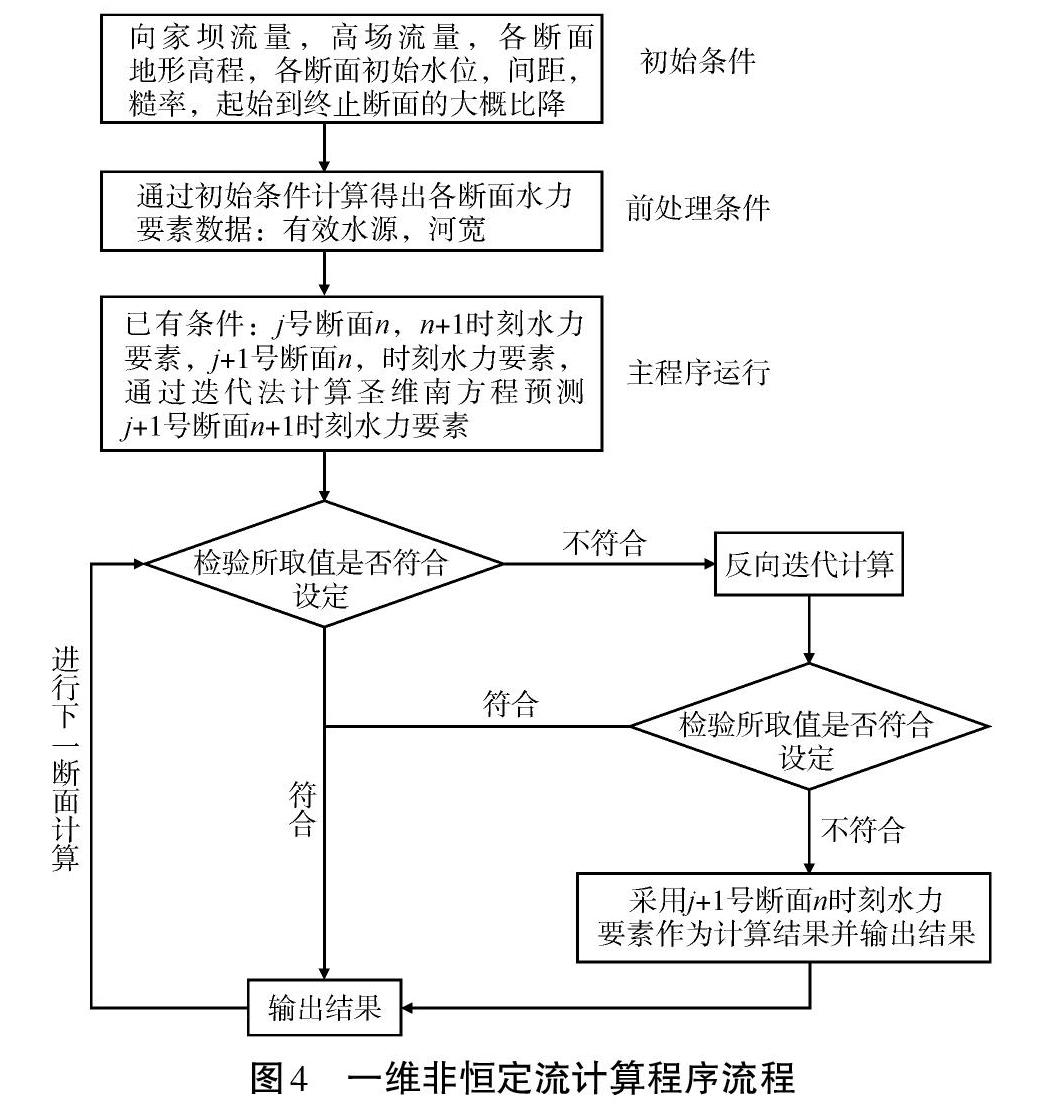
四点迭代法对于叙泸段非恒定流的计算，优势在于能判定所得值是否符合条件，即比较相邻断面节点在临近时刻的流量变化值，进而判定下一时刻的水位是上涨或跌落，以及当设定的流量变化极小或波尚未传导到相应断面时候，可能出现程序反复迭代，当发现流量变幅取值过小时，对水位、流量进行修正。

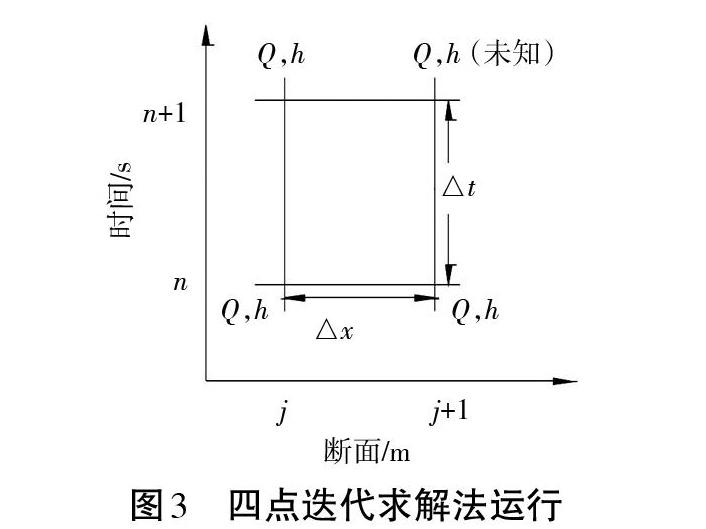
（1）四点迭代求解法意义。已知n时刻j断面，j+1断面的流量Q和水深h，n+1时刻j断面的流量Q和水深h，求n+1时刻j+1断面的流量Q和水深h，四点迭代求解法运行如图3所示。

通过圣维南方程求解求n+1时刻j+1断面的流量Q和水深h。

[∂q∂x+∂h∂t=0]  （1）

[τ0ρ=ghJ-∂q∂t+2v∂h∂t+v2-gh∂h∂x] （2）

式中：q为单宽流量，m/s;h为水深，m;[∂t]为时间n时刻和n+1时刻之間的步长，m;[∂x]为断面j和断面j+1之间的距离，m;[τ0ρ]为床面剪切应力项，可以写为[τ0ρ=ghq2K2]，其中K为流量模数，为常量纲;J为比降，%;v为流速，m/s。其中：

[∂q∂x=qn+1j+1-qn+1jΔx]  （3）

[∂h∂t=0.5hn+1j+1+hn+1j-0.5hnj+hnj+1Δt]

=[dhnj+1+dhnj2Δt]                                          （4）

[∂q∂t=0.5qn+1j+1+qn+1j-0.5qnj+qnj+1Δt]=[dqnj+1+dqnj2Δt] （5）

[∂h∂x=hn+1j+1-hn+1jΔx]                       （6）

式中：[qnj]为j断面n时刻的单宽流量，m/s;[hnj]为j断面n时刻的水深，m;[∂h]为断面j和断面j+1之间的水位差，m;[∂q]为断面j和断面j+1之间的流量差，m/s;[dhnj=hn+1j-hnj]，为j断面n时刻到n+1时刻水深的变化;[dqnj=qn+1j-qnj]为j断面n时刻到n+1时刻单宽流量的变化，m/s。

已知[hnj， hn+1j， hnj+1， qnj， qn+1j， qnj+1]，通过假定[dhnj+1]即可推求[hn+1j+1]，然后通过连续性方程求解相应[qn+1j+1]，再代入运动方程检验是否符合，若不符合，则在原基础上对[dhnj+1]进行累加（减），进行迭代直到得出相应值为止。

（2）方法优点。叙泸段非恒定流集合了以下特点：①水深流量变化较为剧烈;②计算河道较长，继而单个计算的时间步长也较长;③水力条件复杂，存在汊流、险滩以及弯道等复杂地形，在验算中极易引起较大误差甚至导致函数不收敛。该方法结合了Preissmann隐式差分法的推求思想和离散格式和显式差分法中的相对稳定解法。对于类似叙泸段水力条件复杂的河流，采用逐级推求调试以达到相应精度。

（3）一维非恒定流数值计算程序流程。在上述计算方法的基础上，针对向家坝至涪陵河段的1 135个一维断面数据，编写了针对一维非恒定流数值计算的程序，其程序流程如图4所示。

3 模型验证

3.1 叙泸段非恒定流传播特性分析

根据水文实测资料查阅，叙泸段的非恒定流传播特性如下[7]。

（1）宜宾（1 043.6 km）常见非恒定流波高在0.8～1.5 m之间时，自水位波峰时刻起向下游传播至观音背（930.1 km）历时约为12～14 h，且波高衰减为宜宾初始波高的1/2左右;其中，宜宾-李庄波高坦化率为17%～23%，李庄-棺木岩河段波高坦化率为

-3.7%～16.7%，棺木岩-江安河段波高坦化率为4%～9%，衰减效果微弱;江安-观音背河段波高坦化率为15.6%～39.6%，衰减效果最显著。

（2）非恒定流条件下流量基值越大时，沿程河道对波的衰减坦化作用效果越不明显;沿程最低水位仅受流量基值影响，而与流量峰值大小无关。随着传播距离的增加，沿程水位最大日變幅整体呈减小趋势，典型工况沿程水位最大日变幅在0.6～1.5 m之间。

（3）典型非恒定流过程传播周期约为26 h，相波长约为217.4 km，平均传播速度为8.4 km/h，且在半个波长传播距离内自波峰起波速沿程减小。随着传播距离的增加，流量变幅衰减趋势减缓，在半个波长距离后衰减为初始流量变幅的54.2%～64.5%。

3.2 试验水槽一维非恒定流计算

在验证编写的一维非恒定流程序准确率和可靠性的过程中，本研究选择了对水槽实测的非恒定流过程进行调试和验证分析。

（1）试验水槽布置。选择重庆交通大学河海学院航道厅的28 m变坡水槽进行试验。水槽为矩形断面的明渠，沿程布置16组超声水位计检测沿程水位变化，采样频率为10 Hz。流量过程采用变频器控制的水泵试验输入的非恒定流过程。

本次试验采用两组非恒定流序列：①最大流量40 L/s，最小流量5 L/s，周期分别为10，50，100 s的正弦波非恒定流;②最大流量40 L/s，最小流量15 L/s，周期分别为10，50，100 s的正弦波非恒定流。

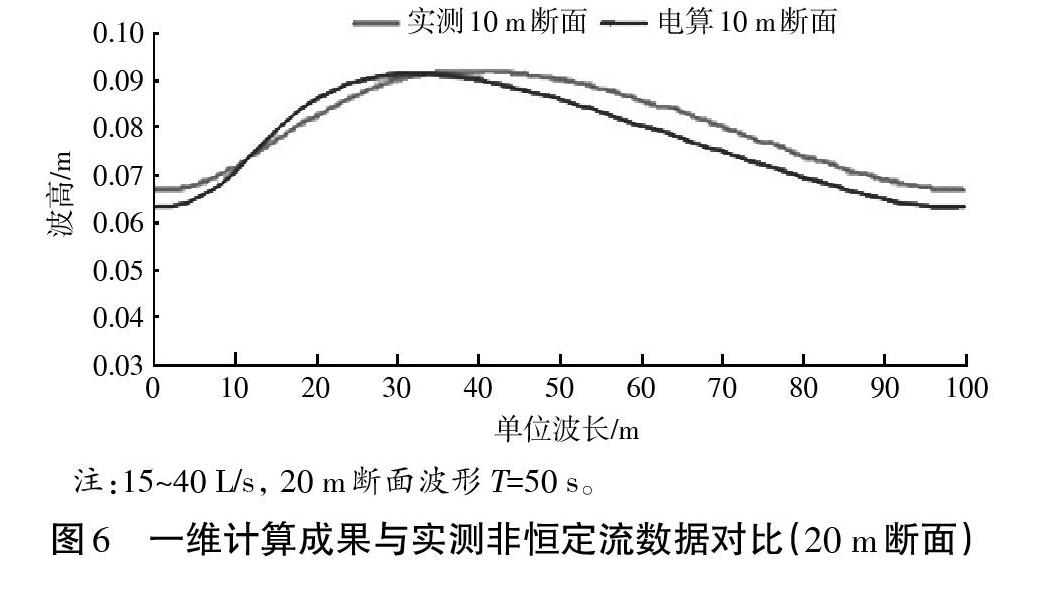
（2）将程序计算成果与水槽实测结果对比分析。从图5～6可以看出，一维非恒定流的计算结果与水槽试验实测数据吻合度较高。周期为100 s，流量序列为15～40 L/s时，计算值与测量值的周期完全吻合，但波高和相位有一定偏差。在10 m断面处，波高实测值为0.026 8 m，计算值为0.033 1;波峰误差约为4.4%，波谷误差约为15%，振幅总误差约为23.5%;相位方面，计算值比实测值延迟约10%周期。在20 m断面处，波高实测值为0.023 7 m，计算值为0.028 4;波峰误差约为2.7%，波谷误差约为6%，振幅总误差约为19.8%;相位方面，计算值比实测值延迟依然约10%周期。

通过结果可看出：在误差允许的范围条件下，一维非恒定流计算程序在运行一段距离和周期后，误差趋向于逐步降低，可进行下一步对于天然河道地形的非恒定流计算。

3.3 叙泸段一维计算模型验证

（1）计算网格断面布置。使用一维非恒定流程序计算宜宾-泸州河段的航道要素，实验设置了1 135个断面，同时为了保持下游水位在枯水期稳定且基本不受上游非恒定流影响，下游终止断面为涪陵乌江入汇口的上游断面，上游起始断面为向家坝下游观测断面，断面的计算范围为长江上游航道里程1 075 km段至536 km段，全长约539 km。

为保证精确反应叙泸段沿程滩险附近的航道要素，在栓疆碛、杨柳碛、筲箕背等11处滩险河段进行了网格加密，保证每个主要滩险至少布置有4～5个断面。叙泸段一维非恒定流部分断面布置见表1。

（2）验证资料收集。课题组收集了向家坝-涪陵河段共49个水文站点的资料，其中宜宾段站点12个。

根据收集的水文资料，一维数学模型的边界条件由上游向家坝的下泄流量过程和涪陵河段的水位过程来控制，其中朱沱断面、寸滩断面由实测流量过程进行修正。

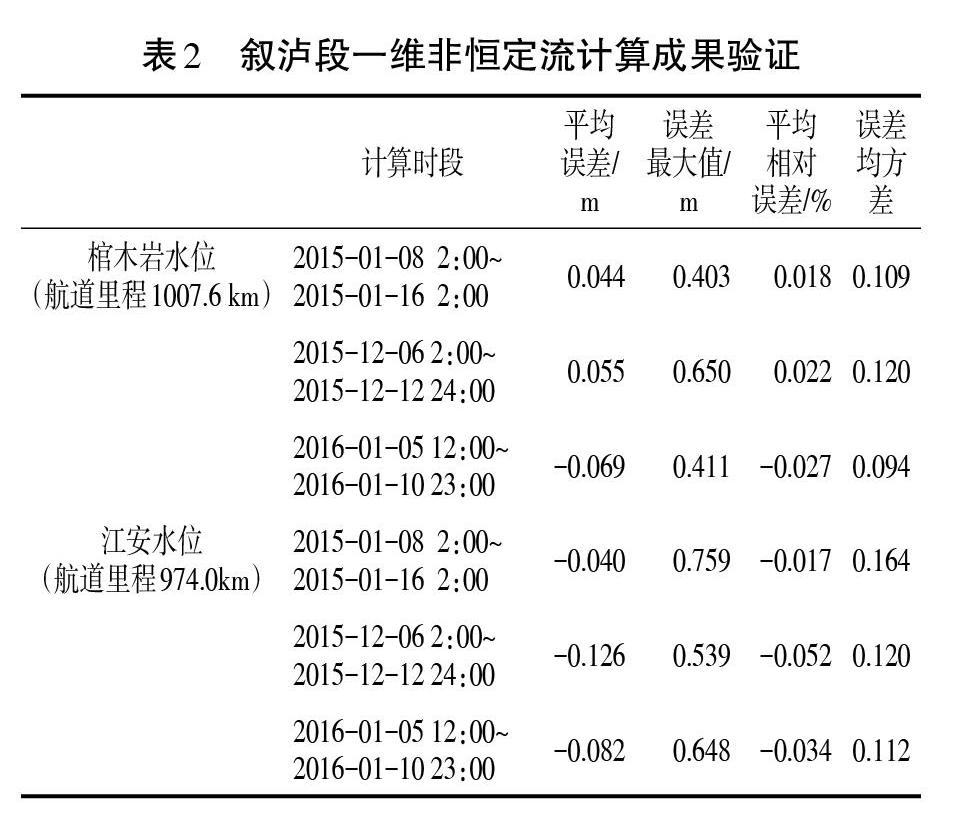
（3）计算结果分析。根据收集到的水文资料，选择叙泸段境内的合江门（航道里程1 043.7 km）、棺木岩（航道里程1 007.6 km）、江安（航道里程974.0 km）3个水位站的水位资料进行验证计算。

根据实测的3个站点水文数据，选择每小时有实测资料和上下游流量过程、水位过程等边界条件的3个枯水期时段进行计算，分别是2015年1月8～16日、2015年12月6～12日以及2016年1月5～10日。

叙泸段一维非恒定流计算成果验证见表2。验证成果表明，数模计算成果与实测水位数据总体吻合度较好。数模预测水位过程与棺木岩、江安站的实测资料平均误差绝对值为0.044～0.126 m，平均相对误差绝对值为0.017%～0.052%。水位誤差最大值范围为0.403～0.759 m，主要出现在非恒定流的波峰或者波谷段，基本是由于水位波形的相位差造成。计算结果的均方差为0.094～0.164，总体符合程度较高。由此可见，水位预报的精度基本满足相关规范要求。除了2015年1月12日的非恒定流水位过程偏差较大，其余时段的水位误差基本在0.2 m范围以内，而且波形的相位差较小。棺木岩站点的水位预报结果与实测资料非常吻合，预报水位误差基本在0.1 m范围以内，且波形的相位差很小。江安站水位误差基本在0.2 m范围内，但是波形相位差相对较大，在水位下降阶段存在明显的波形滞后。棺木岩站点的水位预报结果与实测资料非常吻合，预报水位误差基本在0.15 m范围以内，而且波形的相位差很小。江安站水位误差基本在0.2 m范围内，但是波形相位差相对较大，在水位下降阶段存在一定的波形滞后。

4 结 论

（1）通过试验确定了一维非恒定流的计算方法，运用四点迭代法求解Saint-Venant方程组，并建立一维非恒定流模型，完成了一维非恒定流的计算程序的编写和调试，采用Matlab语言实现一维非恒定流的连续迭代计算，最终模拟计算的结果在误差允许范围内。

（2）本次研究选择对水槽实测的非恒定流过程进行行径调试和验证分析，验证了编写的一维非恒定流程序的准确率和可靠性。将模型计算结果与水槽试验数据相比，波峰误差约为2.7%，波谷误差约为6%，振幅总误差约为19.8%，计算误差满足规范误差范围的要求，一维非恒定流程序准确率和可靠性得到验证。

（3）针对宜宾-泸州河段的航道要素，在向家坝至涪陵河段布置了1 135个断面，采用上述编制的一维程序计算非恒定流条件下的沿程水位变化。计算结果表明：水文测站的计算平均误差0.03～0.08 m以内，平均相对误差在0.02%以内。

参考文献：

[1] 王世平， 王渺林， 姜利玲. 向家坝水电站运行调度对坝下游水位日变幅影响分析[J]. 水利水电快报， 2015， 36（8）：30-32.

[2] 古宇翔，杨胜发，黄岱，等.非恒定流条件下叙泸段航道水深资源利用研究[J].水运工程，2020（10）：99-105.

[3] 张有林， 李文杰， 张谧，等. 向家坝枢纽非恒定泄流对落锅滩河段航道通航条件的影响[J]. 水运工程， 2018， 548（11）：100-105.

[4] 张绪进， 胡真真， 刘亚辉，等. 向家坝水电站日调节非恒定流的传播特征研究[J]. 水道港口，2015，36（5）：414-418.

[5] 蔡新永，蔡汝哲，李晓飚，等. 向家坝非恒定流对航道通航条件影响的试验研究[J]. 水运工程，2017（2）：77-82.

[6] 周晓岚， 刘江， 罗秋实，等. 河道一维非恒定流数值模拟深化研究[J]. 武汉大学学报：工学版，2010，43（4）：443-445.

[7] 薛飞龙，胡江，杜思材，等. 叙泸段河道非恒定流作用下水力参数的变化[J]. 水运工程，2017，10（535）：151-157.

（编辑：唐湘茜）

Verification of prediction model of channel water level change in Xulu section of Yangtze River trunk line under unsteady flow

ZHANG Wen1， FU Xuhui2，3， TONG Qing2，ZHAO Zhizhe3， LUO Yuanyuan3， HUANG Dai4

（1. Yangtze River Yibin Waterway Bureau， Yibin  644000， China;   2. National Inland Waterway Regulation Engineering Technology Research Center，Chongqing Jiaotong University， Chongqing 400074， China;   3. Hohai College， Chongqing Jiaotong University， Chongqing 400074，China; 4. Institute of Engineering， Hokkaido University， Hokkaido 060-8628， Japan）

Abstract： The operation of Xiangjiaba Hydropower Station on the Jinshajiang River has brought great benefits to the society and economy since its operation ， but the unsteady flow process has brought adverse effects on the passage of ships in Yibin-Luzhou section of the upper reaches of the Yangtze River. In order to reduce the losses caused by water level changes and ensure ship's smooth passing the dangerous rapids in the waterway， this study puts forward a one-dimensional unsteady flow mathematical model and calculates the process of runoff and water level along the waterway in the Xulu section. The final calculation error meets the requirements of the standard ， and the accuracy and reliability of the one-dimensional unsteady flow program are verified， that is， the conclusions can be used to analyze the characteristics of unsteady flow along the waterway in Xulu section and the variation law of waterway elements affected by unsteady flow .

Key words：unsteady flow in Xulu section; water level prediction model; four-point iterative method; modelling verification