信息化时代背景下概率论与数理统计混合式教学模式研究

孟珂 赵中

（黄淮学院数学与统计学院，河南 驻马店463000）

0 引言

概率论与数理统计是高等院校理工类专业必修的公共基础课，现已发展成为一门独立的一级学科[1]。此课程以高等数学和线性代数基础课程为基础，与文科、社科类存在明显差异，具有内容丰富、抽象、课题新颖、理论性与客观性强、应用性强、交叉性强、推理逻辑严密的学科特点。课程开设在大二上学期，课时为48学时，内容多，课时少，目的在于培养学生的逻辑思维及数据分析处理能力，把专业知识运用到实践中，用专业素养解决实际问题，以此提高创新意识。

1 研究提出背景及现状分析

学情分析：大学二年级的学生，对于学校新环境、大学生活方式已经适应，因此，二年级就处于学习兴趣和热情的最佳时期。他们思想活跃，受新时代信息化影响较深，对于新事物、现代技术接受能力强，敢于探索发现新知识。但个体间数学基础知识存在差异，自我学习管控和意志力方面偏弱。

教学现状：由于学科内容抽象，逻辑性强，绝大多数教师采取单一的“填鸭式”传统教学，整个教学过程以教师板书并结合PPT课件进行，课程沉闷无味，这难以集中学生注意力，从而降低了学生的学习兴趣与信心。

2 混合式课堂教学设计

混合式课堂教学模式是一种线上+线下的现代化混合教学，强调结合传统教学模式和现代信息化资源优势，鼓励全体师生充分利用现代信息化技术推进教学，充分实现以学生为主体，教师为主导的教育理念，实现全员参与。目前，在线学习资源平台有很多，如慕课、学习通、雨课堂、学堂在线[2]，本文主要基于学习通在线学习平台辅助进行混合式教学模式研究。

2.1 设计理念

以学生为中心，全面落实立德树人根本任务，充分借助信息化手段——学习通平台，为党为国培养拥有丰厚专业知识、具有数据处理和逻辑思维能力、创新精神和高尚道德品质的符合时代发展要求的全面人。

2.2 设计思路

概率论与数理统计混合式课堂教学设计思路如下图1所示。

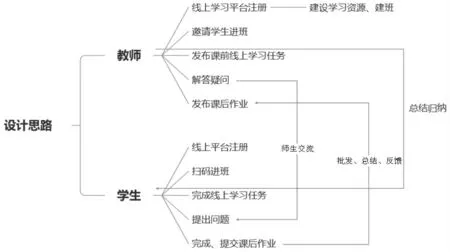
图1 概率论与数理统计混合式课堂教学设计思路

2.3 实施步骤

2.3.1 课前

（1）资料准备。教师依据教学大纲进行章节划分。组建教学团队，进行概率论与数理统计的课程录制，并上传至视频资源。或整合网络共享资源，进行资源优化并上传。此环节可以结合教学内容搜集相关概率发展史或趣味史，以及与教学内容关联的贴切实际的新闻时政案例，从而更好地吸引学生兴趣，提升学生数学素养的同时实现德育功能。（2）上传课程资料。如电子教材、教学大纲、教案、课件等供学生自主查看。（3）建立完善题库。学习通的题目设置类型众多，可满足教师课堂检测以及发布课下作业的需求。（4）建立班级。联系班长分享班级二维码，邀请学生加入班级课程。（5）教师通过移动终端发布学习内容和要求，学生结合自身情况，利用碎片化时间进行知识预习，为进一步学习做铺垫。

2.3.2 课中

（1）借助学习通平台完成在线签到，第一时间获取学生到课率，出勤情况；（2）在学生已经通过线上平台进行复习和预习的基础上，教师发布学前测试，了解学情并及时反馈测试结果，结合实际学情介绍本节课的学习目标；（3）师生面对面，教师逐一细化知识要点并进行讲授，对重难点补充总结，强化相应典型例题；（4）师生共同参与交流式学习，学生积极向老师提出问题，教师第一时间解答疑惑，对问题进行分析；（5）师生共同回顾要点并进行总结。

2.3.3 课后

（1）通过学习通作业题库发布作业，及时检测学习效果，并反馈至每位同学，引导学生及时查找问题，思考反馈；（2）教师通过平台数据记载，查看了解学生在线学习情况，并计入学期成绩综合评定；（3）利用线上资源，进行教学资料补充，拓展学生的认知领域，及时更新教学案例，把抽象的理论方法应用到实际问题的解决中；（4）成绩评定多元，通过线上学习数据，线上作业测评、期中测试、单元测试考核结果，综合线上签到，课后活动答疑活跃度进行多元化成绩评价。

3 案例分析——离散型随机变量数学期望

3.1 学生提前观看学习通教学视频

通过视频《赌徒挑战数学家帕斯卡的故事》，了解数学期望来源，初步认识离散型随机变量数学期望[3]。

引入视频动画，创设情景—奥运会气步枪作为案例。

案例1：观察甲乙两名运动员10次射击的成绩，见下表1。

表1 甲乙两名运动员射击成绩

平均中靶环数是衡量射手的射击水平的重要指标，记平均中靶环数为x，则：

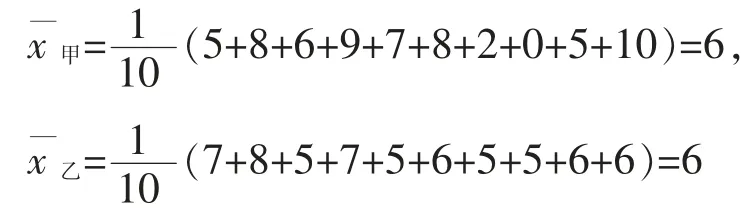
教师引导启发学生思考以下四点：

（1）两名射手的平均中靶环数相同；

（3）增加射击次数，频率会稳定在某一个数值即概率；

（4）把变量取值的平均水平抽象出加以讨论，得到本节内容—数学期望的概念。

3.2 参与式学习——教师总结归纳概念

设离散型随机变量X的分布律为

P（X=xk）=pk，k=1，2…，

通过生活实例激发学生学习兴趣：

案例2：车站每天上午8：00~10：00，每1小时恰有一辆班车到站，到站时间随机，且每个小时到站相互独立。规律为：8：10~9：10到站概率为0.2，8：30~9：30到站概率为0.5，8：50~9：50到站概率为0.3，某人8：25到达车站，问此人候车时间数学期望？

学生自主答题—教师总结。贴近案例，更加生动。

3.3 总结

学生总结数学期望的定义及运用，老师进行补充和提升。

要素1：数学期望的定义；要素2：运用数学期望的知识解决实际问题。

3.4 发布作业——学习通平台

某市在对重点区域10万人筛查新冠肺炎疾病，大规模进行核酸检测时，可选用单采和采两种形式：单采即每个人单独进行核酸采样，这就需要10万试剂难免造成资源过度消耗；混采是指按照k人一组进行分组，对k个人单独采样的核酸进行混合检验，若混合检验结果成阴性，则k个人核酸检测结果均为阴性，若混检结果为阳性，则需要迅速对k个人分别进行单独采样，此时，k个人一共进行了k+1次检验。现已知每个人核酸检测呈阳性概率为p，每个人核酸检测结果相互独立，若p很小，为了减少检验成本的浪费，通常选用第二种混检方式。问：若采用混合检测，k取什么值最合适？

学生作答，并通过学习通线上提交答案。

结合实际案例进行教学。吸引学生兴趣的同时也起到了思政教育的作用。

4 混合式教学模式的意义

教学模式更具创新性。通过融入线上资源，使理论知识的讲授更加深厚，易于理解。借助信息化技术丰富教学案例，变枯燥无味的课程更加生动多元化。利用计算机仿真模拟动画，更加直观地展示教学，更好地集中学生注意力，吸引学习兴趣。

教学过程更具系统性。通过线上线下一体化教学模式，把课前—课中—课后的教学全过程有效衔接在一起。课前利用学习通平台，使学生充分自主预习，同时教师发布题目，对学情进行了解；课中结合学情，进行知识重点讲解；课后利用平台发布作业，同时完善课程线上资源，教学过程更系统。

教学效果更具实践性。利用信息化资源结合相关理论知识寻求生活实际，向学生传授如何把理论知识更好地运用于实践，从而内化为自身的科学素养和技能。揭示理论来源于实践，也能够更好地指导实践的哲学意义。

教学内涵更具时代性。线上测评覆盖全体学员，并第一时间进行反馈，增加了师生互动，提高了师生团队交流学习能力，是新时代高校教育“以学生为中心”内涵的具体体现，有利于培养出一批有逻辑思维和创新能力更强的新时代青年。

5 结语

利用信息化技术平台对概率论与数理统计实施混合式教学，意义重大且深远。但也要认识到自身存在的不足，线上教学资源对自控能力差、自觉性弱的学生似乎很难达到效果，部分同学存在侥幸心理，认为线上学习资源可以任意时间观看，所以，线下教师的讲授就可以不听，只要后期自行观看就可以补上。实际上，这样的学生往往正是自主性差的，他们后期不但没有及时补上功课，反而因为拉下太多，从而在学习中举步维艰，最终丧失学习兴趣与信心，自暴自弃甚至有放弃学习的念头。因此，在混合式教学模式实施过程中，教师要格外关注学生的学习态度，及时跟进学习动态，发现问题及时沟通，并给予解决对策。同时，作为教师不能过分依赖于网络教学资源，而是通过整合资源进一步反馈自身教学，深度思考以提高自身教学技能。