航空兵战术任务规划系统二三维一体化显示设计与实现

董鸿鹏，张 贞，彭紫微

(中国人民解放军92728部队，上海 200436)

航空兵战术任务规划系统是一种在飞机平台性能和作战使用环境的约束下，根据上级指挥所分配的作战任务，充分利用作战态势情报、战场环境信息、目标特性和武器、航电等装备的技术性能，以最优方法设计任务机会，实现空中作战效能最大化的任务支持系统。而航空兵战术任务规划系统中包含有海量的地理信息数据，如二维航空图、二维地形图、三维影像图、DEM高程数据、倾斜摄影数据、气象数据以及作战目标和态势信息等等，具有军用地理信息系统(geographic information system，GIS)的功能特点，如图层数据管理、实现屏幕显示信息载负量控制、地理信息要素编码、军事标图、态势部署等。

1 航空兵战术任务规划系统二三维显示一体化需求

二维平面地图和三维地球是航空兵战术任务规划系统在进行作战行动方案制定时重要的交互界面。系统中的二维地图可用于显示航空区域的平面态势信息，三维地球则可将战场信息进行立体化的表达，如展示地形地貌、立体显示火力范围，便于指挥员排兵布阵和制定详细的作战行动方案。

二维地图和三维地球有多种数据格式，包括海图、航空图、高程图、卫片图、倾斜摄影图等等，在制定作战任务尤其是多军兵种联合作战任务时，需要经常联动切换以一体化的方式进行显示。这种二三维一体化显示方式可充分利用两种显示方式的优点对战场态势进行更全面的分析，如立体化显示战场上的气象情况、地形地貌、作战区域等，增强对整个战场态势信息的把握，减轻使用者的脑力劳动。

由于军事任务的保密性，各个战术编队领受的作战任务往往不同，需要对作战地图根据不同作战单元进行切割分发，这就对航空兵战术任务规划系统的二三维一体化显示提出了更高的要求。

2 二三维一体化设计方案

随着计算机软硬件水平的不断发展，国内外各种二三维GIS软件层出不穷[1-2]，但由于军用软件在显示效率、可靠性和安全性等方面的特殊需求，应使用编译源码(如C++、JavaScript等)公开的功能库或直接用底层三维绘制引擎OpenSceneGraph(OSG)为基础进行框架构建和开发而不是各种封装库，以提高地图的绘制效率和系统的稳定性。

2.1 架构设计

航空兵战术任务规划系统由于其功能的多样性和复杂性，为保证系统稳定运行各个功能模块在设计时均是以功能插件的形式按规定的协议与系统主框架进行交互，二三维地图组件更是如此。二维地图和三维地球组件是整个任务规划系统交互的基础，其使用的数据或功能指令函数均需与系统中其他组件进行交互，由系统框架统一管理，流程如图1所示。

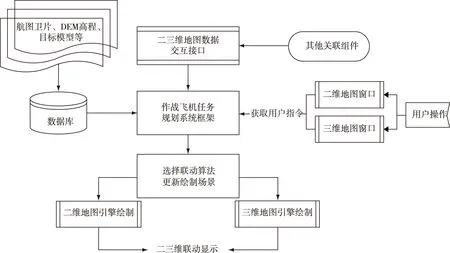
图1 作战飞任务规划系统框架

方案中系统数据库的数据由系统框架统一调用，其中如任务区域、静态部署等二三维地图组件统一显示的数据是由框架统一发布管理，而二维航图、二维军标、三维模型和倾斜摄影等二三维地图组件分开使用的数据，则根据系统设置由二三维组件根据具体场景选取相应的绘制函数分别进行绘制显示，以提高系统显示效率[3]。同时二三维地图组件与其他组件的交互，如威胁分析组件、航线规划组件等，则也是通过系统框架统一控制管理。

二三维显示一体化是以消息驱动的方式进行管理，即先由二维或三维地图界面窗口采集用户操作命令，根据响应消息由系统框架在控制层调用二维或三维地图的功能函数来响应需要实现的动作，如标注军标、显示目标模型、绘制作战区域或运动轨迹等。因此航空兵战术任务规划系统的二三维显示一体化包含两方面的内容，一是二三维地图数据绘制一体化；二是二三维地图联动一体化[4]。

2.2 数据绘制一体化

航空兵战术任务规划系统根据使用需求，可将二维和三维地图组件的基础绘制函数根据绘制对象分为点、线、面、文本四大类，功能接口分为环境接口、工具接口、视点接口、标绘接口(点、线、标牌、多边形、模型等)、倾斜摄影加载、布告板显示、各类特效绘制等[5]。当二三维地图进行数据绘制时，根据系统框架发送的数据，分别使用不同的绘制函数实现数据不同形式的显示，如绘制目标车辆时，二维地图组件在指定位置绘制相应军标；三维地图组件则同步绘制同一位置相应的三维模型。

二三维地图中的各种显示功能如LOD(Levels of Details)数据分层显示、LOD防拥设置、地物查询等也都是依靠系统框架进行统一的设置和管理，由系统框架对数据根据的显示级别进行筛选，再将相应数据发送到二三维地图组件进行绘制显示。

2.3 地图联动一体化

当用户操作二维地图或三维地图中的一个窗口时，另一个窗口会自动同步移动到相同的区域和视角，当二三维的地图范围不一致时，能根据自身数据区域限制二维地图或三维地图的跳转或移动命令[6]。地图联动一体化主要是通过一系列的坐标转换和函数计算以利用交互中事件触发机制的方式，保持二维地图窗口显示的地理坐标范围与三维场景的空间坐标范围位置变化同步。

3 二三维地图显示一体化算法

二维地图通常是按照投影计算方法将地球表面的点投影到平面上，是球面坐标系映射到平面直角坐标系的变化过程，如常见的墨卡托投影、兰伯特投影等，因此其在绘制时显示距离乘以比例尺系数即为真实距离。三维地图绘制时是基于计算机图形学根据视觉原理计算三维投影矩阵，使用可变比例尺，特别是当视点俯仰角接近零即视线与地面近似平行时，可显示出无限远的场景范围，从而绘制出具有空间感、距离感的三维地球[7]。由于二维平面地图和三维地球的绘制数学原理不同，导致了两者在进行一体化同步联动时会不可避免地出现误差，如点选同一位置或在不同地图范围内移动浏览窗口发生偏移。

3.1 矩形区域跳转法

矩形区域跳转法是指当用户操作二维或三维地图中的一个窗口时，另一个窗口会根据接收到传递的矩形区域进行联动，即通过传递当前屏幕的四点坐标进行联动。本文以二维地图接收命令定位三维地图为例，三维地图接收命令定位二维地图的算法部分为其实现的逆过程，在此不再赘述。

首先三维地图获取二维地图传递而来的当前屏幕四个周边点的经纬度A1、B1、C1、D1，利用大地坐标转换为空间直角坐标公式，即公式(1)，求得世界坐标系下的点A2、B2、C2、D2。三维地图联动二维地图即用空间直角坐标转换为大地坐标公式(2)。

大地坐标转换为空间直角坐标为[8]

(1)

空间直角坐标转换为大地坐标：

(2)

式中：e为椭球体第一偏心率，N为卯酉圈曲率变径，X、Y、Z表示大地坐标系中某一点的坐标，B、L、H表示空间坐标系中某一点的纬度、经度和高度值。

然后根据OpenGL绘制生成的透视投影矩阵M，即公式(3)，与显示视椎体的变换函数，即公式(4)，可求得当前近椎体平面的上、下、左、右、近、远距离[9]。

(3)

视椎体变换函数

(4)

根据世界坐标系下的点A2、B2、C2、D2，可求得其构成矩形区域的中心点的高度和宽度，由于视点变换不会修改观察矩阵的张角，因此转换前视椎体的近平面宽度与视点到近平面距离不会发生改变，可以根据近平面的宽度和视点到近平面的距离，利用相似三角形求出矩形宽度填满屏幕下的视点到矩形中心点的距离，如图2所示。

图2 视椎体的空间示意图

同理根据近平面的高度和视点到近平面的距离，可以求出矩形高度填满屏幕下的矩形中心点到视点距离，如图3所示。图3中实线表示三维地图范围，虚线为计算得到的地图范围。最后比较选取屏幕或投影矩阵中距离较长的边，根据视点具体位置设置视角相机的观察矩阵即可。

图3 屏幕填充范围示例

这种计算方法适用于在任务规划系统中快速显示局部地区或某个具体目标等，或对显示内容有高刷新率需求，常用于低纬度区域的变换计算。由于三维地图显示的弧面性，在高纬度地区和大范围时联动时使用该方法计算时会产生较大的偏移误差。

3.2 比例尺跳转法

比例尺跳转法是指当三维地图联动二维地图时，二维地图传递的同步数据为其地图当前中心点A点经纬度和二维地图比例尺。本文定义的比例尺是指屏幕显示的100个像素点在二维或三维地图上对应的实际公里数。具体计算过程如下：

1)首先与矩形区域跳转法相同，利用式(3)和(4)获得当前显示视椎体的显示状态，即近椎体近平面的上、下、左、右、近、远距离；

2)根据二维地图传递的比例尺，可求出100像素下对应三维地球投影距离L；

图4 三维地球在视椎体内的相似三角形

3)利用球表面已知航向和距离求另一点经纬度函数，即式(5)和(6)，求出距中心点A、距离为L/2，方向角为90度和270度的点B、点C；

4)使用坐标转换公式(1)，将点B、点C转换为世界坐标下的点B1、点C1，从而求出B1、C1的中心点D和点B1、C1的直线距离L2；

5)根据相似三角形可得100/zNear=L2/OD，进而求出视点O距离点D的距离OD；

6)最后利用osgEarth的setViewpoint函数设置视点位置即可，中心点为D的经纬高，距离为OD，方向角为0°，俯仰角为-90°。

Al、Ab、Bl、Bb，分别表示A、B点的经度和纬度，P点表示北极点，θ表示大圆始航向，a、b、p表示A、B、P三点对“弧”两端点与地心连线的夹角，T表示AB两点间的球面距离、R表示地球平均半径。已知球表面A点经纬度、航向θ和A、B两点间的距离，可根据式(5)、(6)求出B点的经纬度。

(5)

(6)

注：因为地球偏心率极低，所以此处可将地球看作球体，计算结果与WGS84坐标系下测量偏差不超过0.5%[10]。比例尺跳转计算方法适用于二三维地图在显示高纬度地区和大区域范围时的联动，可根据精度需求可适当修改所需像素数值大小，并通过增加限制条件实现显示范围的锁定。

3.3 透视投影跳转法

一般二维地图使用的数据格式是正交投影下的平面直角坐标系，但也有部分地图数据使用的是三维透视投影的球面坐标系，此时进行三维跳转时只需要保持视角相机正视二维地图即可。因此对该类使用与三维地球相同的地球椭球体坐标系的二维地图数据，只需要保持二三维相机的观察点经纬度和相机距离观察点的距离相同即可通过计算机图形学的投影机制自动保持二三维同步。具体计算过程如下所示。

首先根据坐标转换矩阵求出本地点转为世界坐标系下的矩阵WM[11]，然后根据式(7)求出相机位置变换矩阵LM，则观察矩阵为LM×WM的逆矩阵。

(7)

式中，d表示相机位置距观察点的距离，xr表示观察点的俯仰角，zr表示观察点的偏航角。

4 实现效果及应用

根据本文提出的航空兵战术任务规划系统架构和二三维显示转换算法设计构建了一套二三维一体化的演示系统，通过消息传递实现对用户在操作任意场景时，如平移、缩放及目标标绘等，另外的一个场景利用算法实时计算视点的位置和高度变化以自动进行同步联动。

图5是演示系统中某一处目标点的二三维一体化效果图，其中a)、b)、c)是居民区目标在三维地图中不同视角下的显示效果，d)是居民区目标在二维地图上标绘军标的显示效果，系统实现了对目标标绘的同步数据绘制。图6是某型地空导弹威胁范围的二三维一体化显示，左侧是二维地图的视图，右侧是三维地图的视图。分别采用了俯视、平视、侧视三种不同的视角作为对比以验证跳转算法的显示效果，可以看出在不同视角下二维地图和三维地图的显示范围均相同，地空导弹目标始终在地图的绘制中心，能够满足使用人员作战方案制定时的计算需求，同时在多次同步跳转后并没有出现场景发生偏移或不匹配的情况。

图5 目标点的二三维一体化效果图

图6 武器威胁范围的二三维一体化效果图

5 结束语

本文设计的航空兵战术任务规划系统架构，能够实现二维地图和三维地图的一体化同步显示，以消息传递的联动机制实现了作战信息数据在内容和空间分析上的一致性。本文分析提出的3种二三维地图显示同步的算法，能够满足用户在操作航空兵战术任务规划系统时二三维地图的同步性需求，并利用演示系统绘制了二三维一体化效果图证明算法的可行性和准确性。本系统在实际工程实践中发挥了关键作用。