高超声速滑翔飞行器驻点热环境不确定性量化评估
2021-12-18丰志伟葛健全张青斌
吴 昊,杨 涛,丰志伟,葛健全,张青斌,黄 浩
(国防科技大学空天科学学院,湖南长沙 410073)
由于速度和突防方面的优势,高超声速滑翔飞行器受到了各军事强国的广泛关注。邻近空间内长时间超高速飞行所带来的严酷气动加热给飞行器防热及结构设计带来了诸多挑战[1]。文献[2]指出,飞行器长时间受气动加热作用后,热变形可能会引起气动特性的变化,从而导致飞行弹道和姿态的变化,影响飞行器的整体性能。目前的数值仿真以确定性仿真为主,即需要给出精确的来流条件、边界条件和物理模型。而气动加热热流受来流条件、几何尺寸、边界条件和物理模型的影响,这些不确定性因素是普遍存在的,当这些因素与实际情况存在偏差时,实际热流就会偏离预示值。不确定性因素的来源主要可分为随机不确定性(Aleatory Uncertainty)和认知不确定性(Epistemic Uncertainty)两大类。前者是由物理系统及其环境固有的随机性产生的;而后者是由于人的认识不足或者信息缺乏所造成的。气动热环境的不确定性量化评估对于高超声速滑翔飞行器飞行试验方案的确定具有重要参考意义。
Bettis和Hosder[3]对高超声速再入流动的不确定度问题进行了分析,研究混合不确定性输入变量对气动热的影响。Brian A.Lockwood等进一步研究了认知和随机不确定性混合传播的优化使用[4],并发展出一种区间统计方法,结合Fay-Riddell驻点热流公式证明其在流体仿真计算中的适用性;Lockwood在进一步研究中提出一种多变量输入情况下省时高效的基于梯度信息的代理模型[5],研究了理想气体和不平衡气体条件下高超声速黏流中热流的不确定性。相比于国外,国内对气动热不确定度量化评估的研究还处于起步阶段。张伟等[6]运用基于非侵入式多项式混沌(NIPC)的方法和基于Sobol指标的方法对Apollo飞船返回舱开展了气动热不确定度量化分析和敏感性分析,得到了驻点和肩部热流不确定度随径向距离变化的规律,为飞船返回舱气动热防护设计提供参考依据,证实了NIPC方法与Sobol敏感性分析方法在热不确定性问题中的适用性,对进一步用于高超声速飞行器的鲁棒优化设计和可靠性分析提供了思路。
本文以某滑翔飞行器为研究对象开展气动热数值预示,选取来流速度、来流密度、来流温度和端头半径4个不确定性变量,利用多项式混沌展开方法对气动热进行不确定度量化和敏感性分析,为飞行试验方案的确定提供理论依据。
1 气动热分析方法
高超声速滑翔飞行器气动热环境可分解为驻点、飞行器前缘和大面积等部位,下面分别给出具体的计算方法。
1.1 驻 点
球头驻点热环境预测采用压缩性修正的Fay-Riddle公式,即
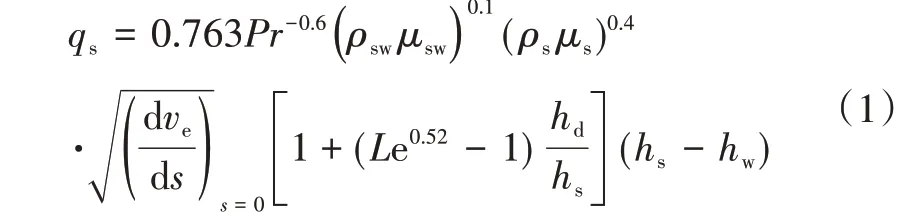
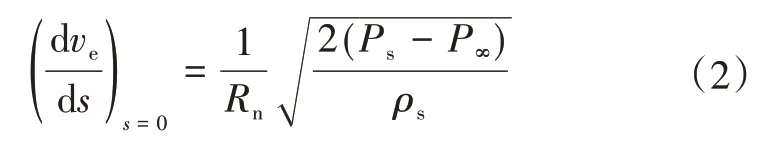

式(3)中,压缩性系数Z与驻点压力和温度相关,采用压缩性系数函数表插值计算。
1.2 飞行器前缘
飞行器前缘的热环境预测采用后掠圆柱理论,即
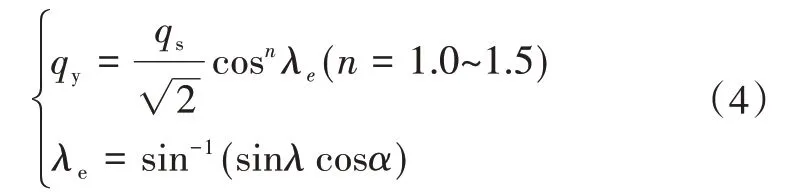
式(4)中,qy为翼前缘驻点线热流,qs为与翼前缘相同半径的驻点热流,λe为有效后掠角,λ为后掠角,α为攻角,指数n取1.2。
1.3 大面积
飞行器大面积的热环境预测采用流线法,计算中考虑变熵效应。本文选用Zoby公式[7]计算热流,该公式是基于Eckert参考焓的可压缩平板摩擦系数关系得到的,计算结果与实验数据和飞行数据均吻合较好。下面分别给出层流、湍流和转捩区的热流计算公式。
(1)层流热流,即
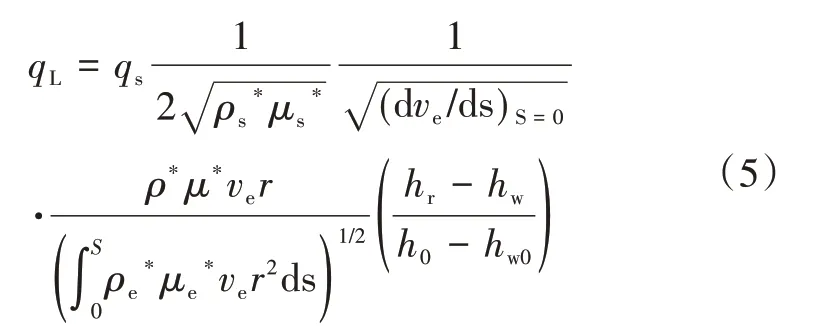
式(5)中,qs为采用Fay-Riddle公式得到的驻点热流。
(2)湍流热流,即
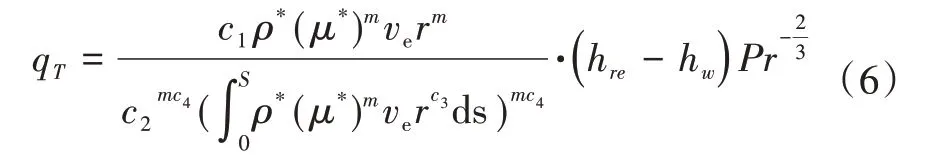
式(6)中,c1,c2,c3,c4,m是速度剖面指数N的函数,分别为

在通常选用的1/7次速度分布中,N=7,但真实情况下N是变化的,由轴对称喷管壁面实验数据拟合出的N曲线[8],即
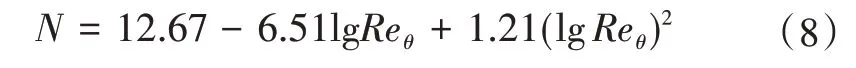
式(8)中,Reθ是基于动量厚度的雷诺数,表达式为
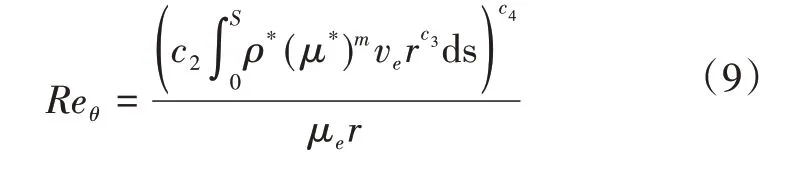
本文根据式(8)和(9),采用迭代方法求解N与Reθ。
(3)转捩区热流,主要采用间歇因子方法计算转捩区热流,即
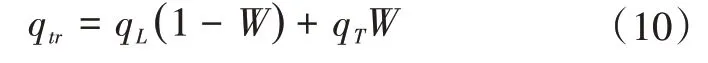
式(10)中,W为间歇因子,变化范围是0<W<1,它与转捩起始位置和转捩结束位置有关,取
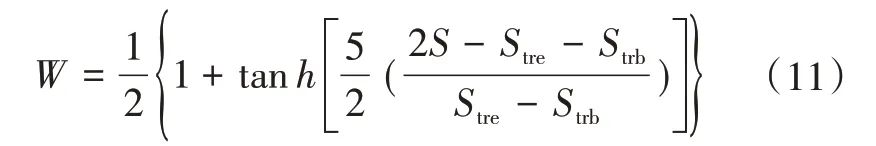
定义边界层外缘当地雷诺数等于转捩雷诺数Retrb的位置为转捩起始点,其位置为Strb。文献[9]总结碳-酚醛端头的飞行试验数据,给出了与边界层外缘马赫数相关联的公式,即
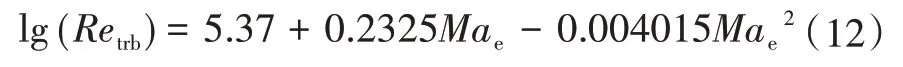
转捩结束点位置为
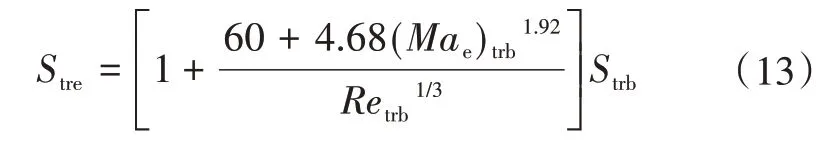
2 不确定性量化评估方法和敏感性分析
本文采用多项式混沌(Polynomial Chaos,PC)法作为均值随机展开,对滑翔飞行器气动热环境进行不确定性量化分析。多项式混沌法基于不确定性的谱表示,相比传统的蒙特卡洛仿真具有更高的效率。
2.1 多项式混沌不确定性量化方法
不确定性谱表示的基本思想是将响应值或随机函数α*分解为由确定性和随机性分量表示的形式,即
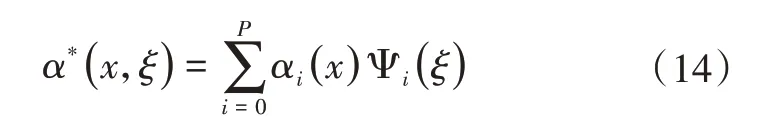
其中,αi是确定性分量,Ψi是与第i模态对应的随机变量基函数,α*假设为独立变量x和n维标准随机变量ξ的函数。式(14)是一个无穷序列,实际使用时对其进行截断处理并保留部分输出模态作为输出。对于p阶多项式混沌展开(Polynomial Chaos Expansion,PCE)和n维随机变量,可计算总阶数Nt,即
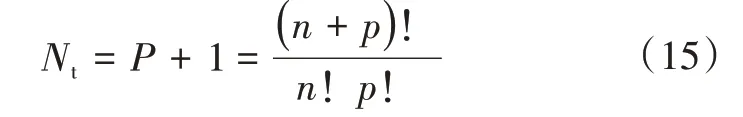
PCE方法的核心是确定展开系数αi,通常可使用侵入或非侵入的方式计算得到。侵入式方法在理论上更为直接,但是对于复杂问题该过程具有耗时长、代价大等缺点。而非侵入式方法,则不需要修改原确定性模型,容易构建表示复杂模型的代理模型。
对于非侵入性多项式混沌(Nonintrusive Polynomial Chaos,NIPC),目前已发展了多种方法,其中在航空航天领域应用最广泛的是配点NIPC法。该方法首先将随机响应面或随机函数近似表示为PCE;然后在随机空间中选择Nt个矢量,每个矢量即为一个采样点,采用确定性模型评估这些采样点,得到式(14)左边;接下来,形成式(16)给出的Nt个方程的线性方程系统;最后求解随机变量的谱模态。
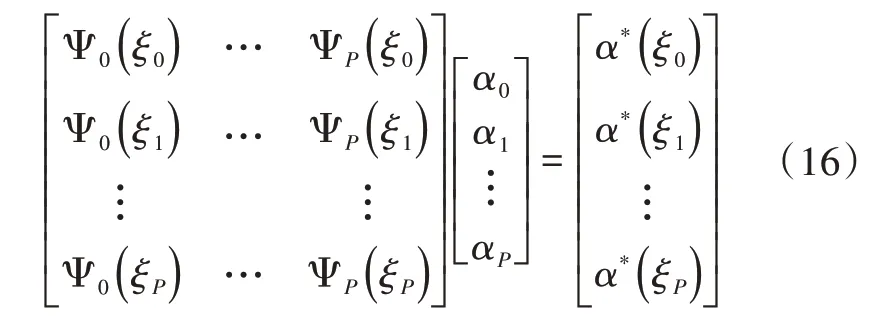
需要说明的是,Nt是用于确定PCE系数的确定性采样的最小数目。如果存在更多的采样且线性无关,则系统为超定方程,可使用最小二乘方法求解。超过所需最小个数的采样使用过采样率(Oversampling Ratio,OSR)表示,定义为实际采样与最小需要采样的比值。一般而言,配点数量可以通过式(15)乘以OSR确定,PCE的精度依赖于配点数量。
2.2 Sobol灵敏度分析方法
Sobol灵敏度分析方法是基于方差的全局敏感性分析方法,通过计算一个或多个输入变量对输出方差的贡献量,以此来评价该输入变量在不确定性模型中的重要性。Sobol指标需要通过Sobol重积分分解(以下简称Sobol分解)计算[10]。
假设通过PCE方法得到多项式函数f(x),x=(x1,x2,…,xn),定义域为In,通过Sobol分解可将该函数分解为如下形式,即
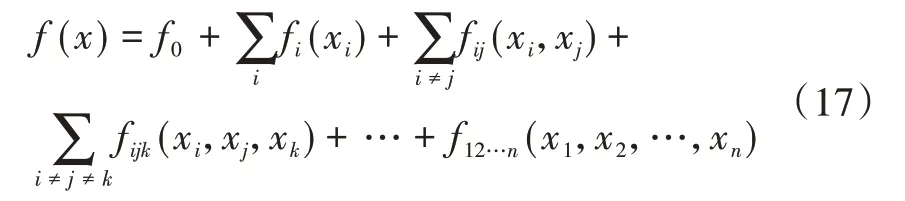
其中,各项按照以下公式分解得到
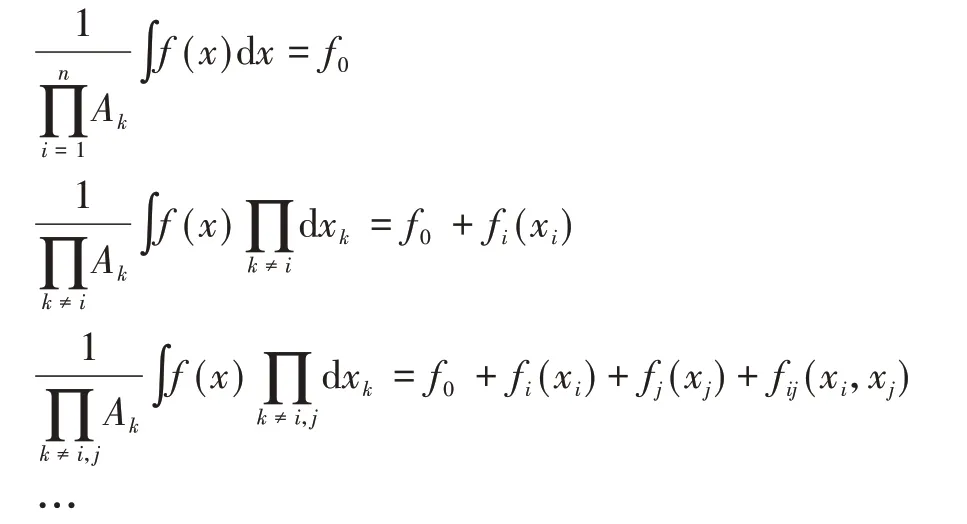
得到式(17)后,可求得总方差,即
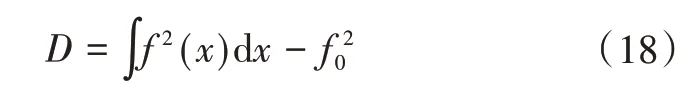
各阶偏方差为
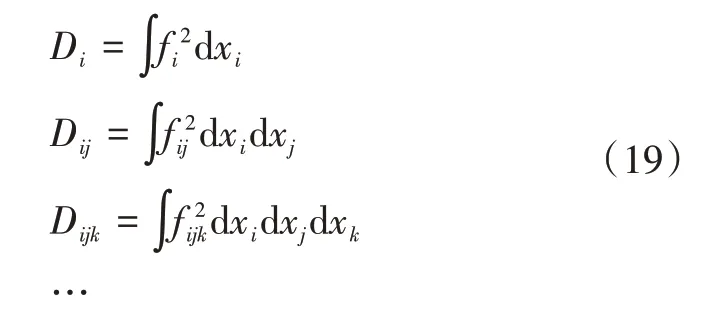
总方差和偏方差满足
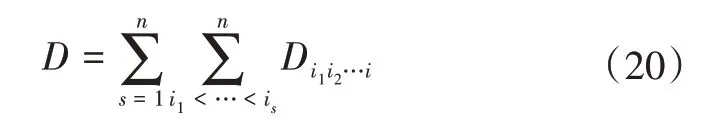
各阶Sobol指标Si1…is的定义为

Sobol指标提供了敏感性的度量,即,每个输入不确定变量Si的贡献以及混合贡献Si1,...,is。输入参数的总组合定义为部分Sobol指标的和,即
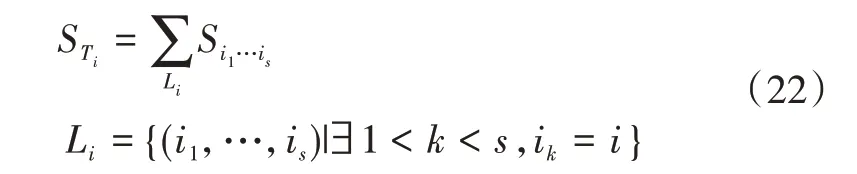
即将所有与变量xi有关的Sobol指标相加,当n=4时,变量x1对总方差的总贡献为
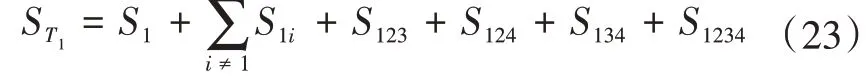
Sobol指标可用于给出每个输入不确定性变量对总方差贡献的相对排序,且能够考虑输入变量和输出指标的非线性相关性。
3 仿真算例
以某高超声速滑翔飞行器端头为对象,开展气动热环境的不确定性量化评估和全局敏感性分析。其中,热环境以辐射平衡热流表示,边界层外缘属性按照激波后属性计算[11],边界层黏性用Sutherland公式计算[12],且壁面压力可假设为边界层外缘压力。
飞行环境及端头半径如表1所示。分析中取4个随机不确定变量:来流速度U∞、来流密度ρ∞、来流温度T∞和端头半径Rn,由于飞行器加工过程中制造误差和飞行环境的不确定性,来流条件的随机波动是存在的。这些变量假设为关于某个均值的正态分布,变量分布和方差系数见表2。

表1 飞行环境及端头半径数值Tab.1 Aviation environment and the radius of curvature of the body
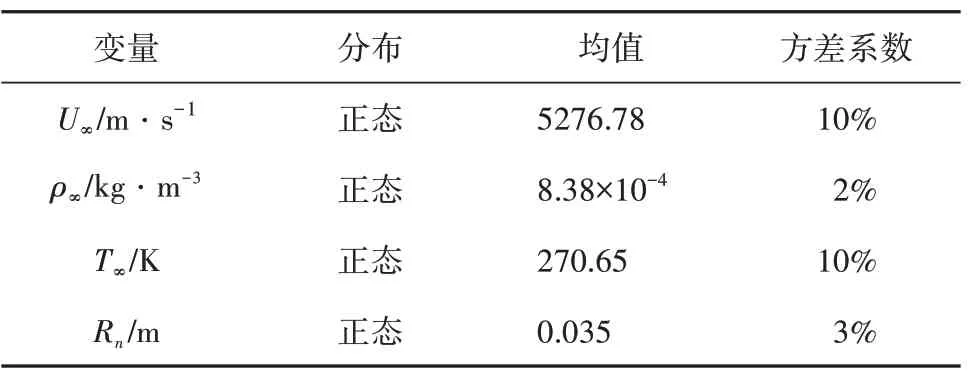
表2 随机不确定性随机变量分布Tab.2 Probability distribution of aleatory variables
由于该问题的不确定变量维数较小,可以使用最小二乘解来比较。对随机不确定性在给定采样规模下分析响应面提供累积分布概率(CDF)的上下边界。当过采样率取2时,能够克服传统配点法的不稳定性,最大程度减少各组配点对响应面的影响。图1为过采样率为2时热流分布的P-box图。相应的95%置信区间为表3所示的下边界2.5%概率水平到上边界97.5%概率水平。
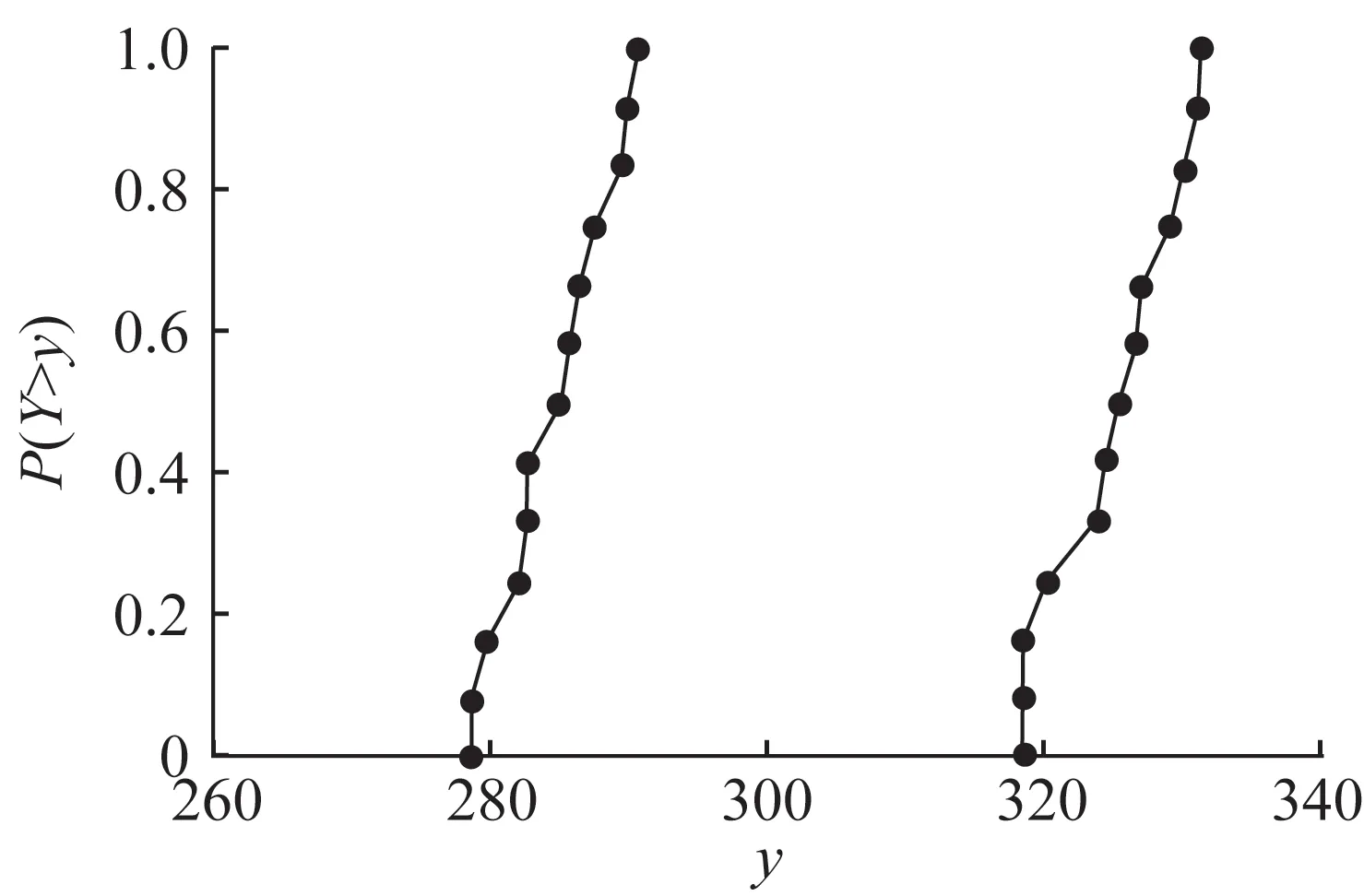
图1 过采样率取2时的热流分布P-box图Fig.1 P-box plots for heat flow(OSR=2)
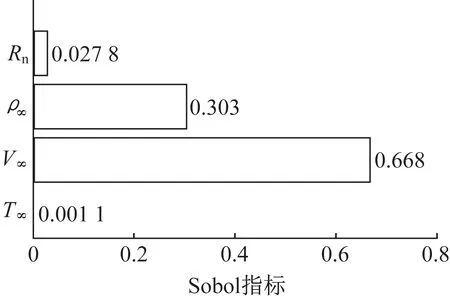
图2 随机变量的Sobol指标Fig.2 Sobol indices for aleatory variables
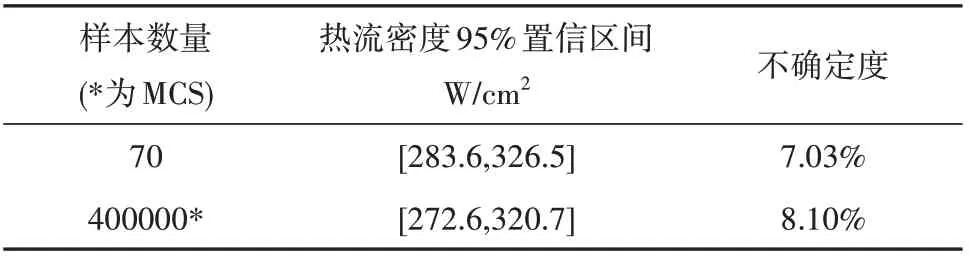
表3 热流密度95%置信区间Tab.3 95%Confidence interval of heat flux for selected samples
4 总 结
本文以高超声速滑翔飞行器为对象开展气动热环境数值预示,选取来流速度、来流密度、来流温度和端头半径等4个不确定变量,采用NIPC方法对端头半径气动热进行不确定量化评估和敏感性分析,得到如下结论:
(1)利用非侵入式多项式混沌方法与大量蒙特卡洛采样所得不确定度区间吻合,表明利用NIPC方法能够在缩短不确定性量化评估时间的同时,得到可信的结果。
(2)给定变量不确定条件下,端头热流的均值大约为305.05W/cm2,不确定度不小于7.03%。
(3)采用基于Sobol指标的敏感性方法,对计算结果进行了敏感性分析,结果表明来流速度变化和来流密度变化对热流不确定度贡献最大,端头半径对热流的不确定度有一定影响,而来流温度变化几乎不产生影响。在高超声速气动热预测中应重点关注来流速度和来流密度的变化。
