基于径向基神经网络的水下自主航行器寻源算法研究

吴宗秀，吴 超

(1. 上海交通大学 船舶海洋与建筑工程学院，上海 200240; 2. 上海交通大学 海洋工程国家重点实验室，上海 200240)

水下寻源着眼于解决利用单个或编队水下航行器对未知分布的信号场进行信号源搜索问题。水下工程领域的许多问题都可以归结为水下寻源问题。包括：失事飞行器黑匣子的寻找、天然气或者水下矿藏的定位、热液喷口搜索[1]等。在这些问题中，未知信号场则相应地可以具体化为声学信号场、化学物质浓度信号场及温度信号场等。水下寻源问题的解决方案对于扩展水下航行器的应用而言有着重大的意义，该领域的解决方法一般有瞬态决策方法、极值搜索算法、高斯过程回归以及神经网络等。

Holland等[2]、Russell[3]分别就未知信号场的寻源问题提出了六边形和Z字型前进路线的搜索策略，通过离散的信号测量以及简单的信号强度对比进行搜索路径的规划。Russell[4]后续将工作拓展到三维场源搜索问题中，瞬态极值策略可以作为寻源问题一种相对稳定的解决方案,但是其决策得出的方向精度不足。自动控制领域的方法在场源搜索问题中亦得到了广泛的应用，Mellucci等[5]、Matveev等[6-7]均运用了滑模控制方法来控制水下航行器的首向进行信号场的极值搜索，其结果显示，滑模控制方法生成的搜录路径相对较长。Cochran等[8]将极值搜索算法(extreme value search algorithm, 简称ESA)运用到水下寻源问题中，通过控制航行器的转向引导航行器进行搜索，该团队在其他研究[9]中增加前进速度为控制参数并且得到了更好的结果，但同时也指出该算法收敛速度较慢的问题。

高斯过程回归(gaussian process regression, 简称GPR)具有良好的函数逼近能力，常用于解决未知信号场的拟合问题。Ai等[10]结合高斯过程回归、Armijo步长准则、递归最小二乘方法和非线性模型预测控制(nonlinear model predictive control, 简称NMPC)进行完备的水下航行器场源搜索仿真。其研究结果表明航行器在搜索过程前期受先验信号场影响明显，在接近先验信号场的最大值区域后转向正确的路径并收敛到真实场源。阎述学等[11]的研究着眼于利用高斯过程回归进行水下信号场的热点采样，通过定义一种与均方差相关的引力模型引导航行器进行多热点未知信号场的自适应采样。相较于传统的割草机和梳型路径，该算法能够以较短的路径实现更准确的拟合。

径向基神经网络(radial basis function neural network，简称RBFNN)具备无限精度的函数逼近能力，能够运用于信号场的估计并且具有结构简单、易于理解的优点。Jeon等[12]通过推导连续时间形式的递归最小二乘法对RBFNN进行在线训练，并控制装有多个传感器的双连杆机械手进行二维灰度图的极值寻找。然而利用RBFNN的寻源算法研究很少考虑神经网络的正则化，实际上正则化对于神经网络的稳定性和泛化性非常重要。

以水下自主航行器(autonomous underwater vehicle, 简称AUV)在热泉区域的硫化氢浓度分布场场源搜索为背景，使用具有增长式结构的RBFNN对未知信号场进行在线无先验渐进拟合，并通过增量式奇异值分解算法加速神经网络的正则化计算，此外还利用动量梯度法解决AUV路径容易陷入局部最优区域的问题。算法的有效性通过单峰值和多峰值硫化氢浓度场中的场源搜索模拟计算进行验证。

1 未知场在线估计

1.1 水下寻源问题描述

1.2 RBFNN介绍

径向基函数神经网络(RBFNN)，具有结构简单、学习速度快、拟合精度高、泛化能力较强和不易陷入参数局部最优等优点，被广泛应用于函数逼近、分类、时间序列预测等诸多领域，其网络结构示意如图1所示。

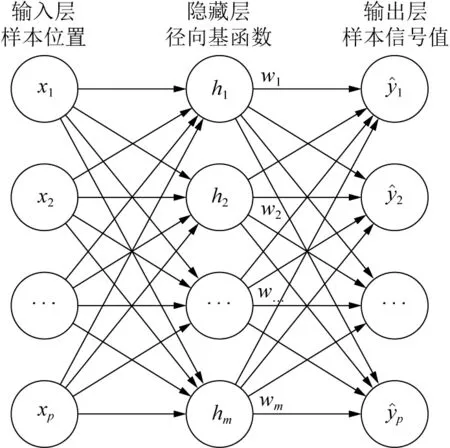
图1 RBFNN结构示意Fig. 1 View of RBFNN’s construction

RBFNN在结构上是严格的三层网络，分别为输入层、隐藏层和输出层。输入层负责信号传递，隐藏层通过径向基函数(radial basis function, 简称RBF)进行从输入层到隐藏层空间的非线性变换，输出层对隐藏层的响应进行加权求和。

选用高斯型径向基函数：

(1)

其中，ωj为权重系数，cj为核函数中心，rj为高斯函数半径。

设计矩阵H，其元素Hi,j=hj(xi)，行数记作p，列数记作m：

(2)

权重向量W可表示为：

(3)

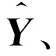
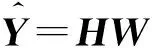
(4)

权重向量可以通过计算伪逆或最小二乘法求取。为了避免矩阵求解中的病态问题以及神经网络的过拟合问题，引入全局正则化操作，对应权重向量求解公式如下：

(5)

其中，参数λ为全局正则化系数，该参数能够提高神经网络的泛化性和计算稳定性，λ的数值需要在网络结构和数据集变化的时候进行优化。

综上，RBFNN对任意输入x∈R2的信号值预测为：

(6)

1.3 RBFNN在线训练

径向基神经网络的预测性能取决于RBF中心{C1C2……Cm}、权重向量W、全局正则化参数λ等。为了实现RBFNN的在线训练，算法应当能够在寻源过程中实时进行以上参数的优化。

1.3.1 径向基函数分配

通过资源分配网络算法(resource-allocating network, 简称RAN)[13]进行径向基函数中心的分配。RAN算法开始时具有较少径向基函数中心，根据新增样本的新颖性决定是否添加径向基函数进行误差消减。

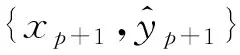
条件1：当前样本位置xp+1与最近的径向基函数中心Cnear的欧式距离超过阈值δ。

‖xp+1-Cnear‖>δ

(7)

条件2：神经网络对当前输入样本xp+1的预测与实测数值偏差大于阈值ε。

(8)

添加径向基函数后神经网络发生变化，需要通过更新正则化参数λ和计算权重向量W进行神经网络的优化。

1.3.2 在线正则化参数迭代计算

神经网络的性能取决于预测的准确度和泛化性，正则化参数λ的引入能够在一定程度上实现二者的平衡，而λ的取值可以通过广义交叉验证误差(generalized cross-validation, 简称GCV)的最小化来决定。首先给出径向基函数神经网络的广义交叉验证误差表达式：

(9)

其中，p为当前路径点个数，P为RBFNN中的投影矩阵：

P=I-HA-1HT

(10)

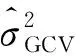
(11)

值得注意的是若直接使用公式(11)会导致每次迭代计算都需进行多次复杂度为O(m3)的矩阵逆运算。观察与矩阵A相关的表达式(5)可以发现，通过设计矩阵H的奇异值分解能够有效简化A的求逆过程进而简化公式(11)各部分的计算复杂度。

首先设截断奇异值分解(truncated SVD)H=USVT，其中U=[u1u2…ur]∈Rp×r、V∈Rm×r为正交矩阵，S∈Rr×r且有如下形式：

(12)

式(11)各部分简化结果如下[14]：

(13)

通过以上简化计算，能够将式(11)的复杂度从O(m3)降低到O(p2),并且只需要在迭代计算前进行一次复杂度为O(p3)的奇异值分解计算，对于重复迭代的计算而言能够节省大量算力，算法的伪代码如下：

Algorithm 1 基于SVD的正则化系数求解Require:SVD分解USVT=H,函数值Y^Ensure:正则化系数λ,权重向量:W1:function REGULARIZE(U,S,V,Y^)2:λ0,λp1,μdiag(S),yUTY^3:while(abs(λ-λp)>0.000 1)do4. λpλ5:λ∑pi=1uiy2i(ui+λp)3∑pi=1λpui+λp∑pi=1λ2py2i(ui+λp)2∑pi=1ui(ui+λp)26:end while7:WV(STS+λI)-1Sy8:return[λ W]9:end function

对不同规模的设计矩阵H利用原版迭代算法和基于SVD改进的迭代算法进行正则化参数求解，设定矩阵H为方阵。设置初始λ=1，并进行50次的迭代。统计改进算法中，总耗时、SVD分解耗时以及迭代耗时与原算法耗时的比值，结果如图2所示。

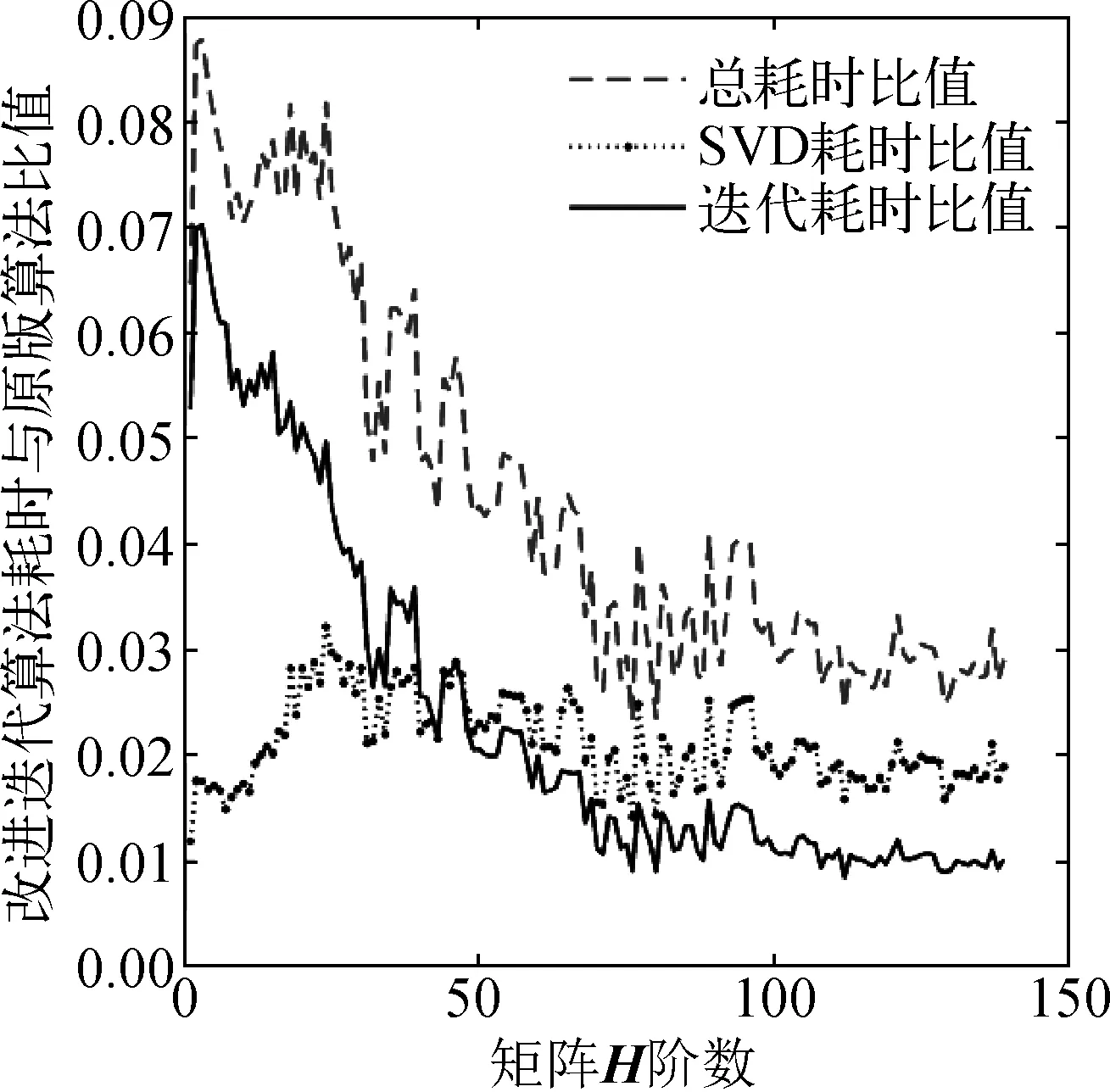
图2 迭代公式计算耗时对比Fig. 2 Time cost of different re-estimation method

从结果中可以观察到，改进算法中迭代计算的耗时与原算法的耗时比值随着神经网络规模的增大而减小，改进算法中的SVD分解耗时与原算法的耗时比值却维持在1/50附近。整体而言改进算法的耗时远小于原算法，但是其中SVD分解耗时的复杂度阶数与原算法相似，需要进一步简化。

1.3.3 设计矩阵H增量式SVD分解

对设计矩阵H进行奇异值分解能够显著降低正则化系数求解的复杂度，却引入了SVD分解的计算复杂度随神经网络阶数增加而增加的问题。因此奇异值分解的简化变得至关重要。观察式(2)中设计矩阵H的结构能够发现，增加样本数据和增加径向基函数实质上是在增加设计矩阵H的行数或者列数。这意味着每次神经网络结构变化时H的主体部分不发生变动。结合Brand的工作[15]利用Hp,m的奇异值分解结果对Hp,m+1或Hp+1,m进行增量式SVD分解，定义Hp,m+1和Hp+1,m分别为增加径向基函数和增加样本数据后的设计矩阵。以下以Hp,m+1为例简述增量式SVD的计算过程。

对设计矩阵Hm有截断奇异值分解，其中Sm阶数为r：

Hp,m=USVT

(14)

Hp,m+1与Hp,m之间存在如下关系：

Hp,m+1=[Hp,mhm+1]，hm+1=[hm+1(x1) ……hm+1(xp)]T

(15)

计算：

(16)

对M进行归一化处理：

J=M/K,K=‖M‖

(17)

设计矩阵运算如下：

(18)

Q=U′S′V′T

(19)

可以得到更新后的奇异值分解：

Hp,m+1=U″S″V″T

(20)

其中，

(21)

通过以上的分解能够将Hp,m的奇异值分解转化为Qr+1,r+1的奇异值分解。并且值得注意的是Q实际上为边对角矩阵，其奇异值分解的计算复杂度可以通过O″ Leary[16]的工作从O(r3)简化到O(r2)。通过以上的简化计算能够将设计矩阵奇异值分解的计算复杂度降低到O((m+p)r2)，在计算中设定比值r/p=0.25。

Algorithm 2 增量式SVD分解Require:原分解:USVT=H新增列:hm+1Ensure:增量SVD: U″,S″,V″,h″T=[H h]1:function INC SVD(U,S,V,h)2:[U'S'V']SVDSUThS|h-UUTh| 3:U″[U(h-UUTL)/|h-UUTh|]U'4:S″S'5:V″V001 V'6:return[U″,S″,V″]7:end function

对不同阶数的设计矩阵增加列数据并求取新设计矩阵的奇异值分解。计算结果如图3所示，能够直观地看到增量式分解显著降低了计算耗时并且效果随着神经网络规模的增大而增大，计算过程在Matlab2019 中进行，考虑到数学计算软件对于计算过程的优化，结果中呈现的计算耗时比例未必能够完全与理论上的计算复杂度分析完全对应。

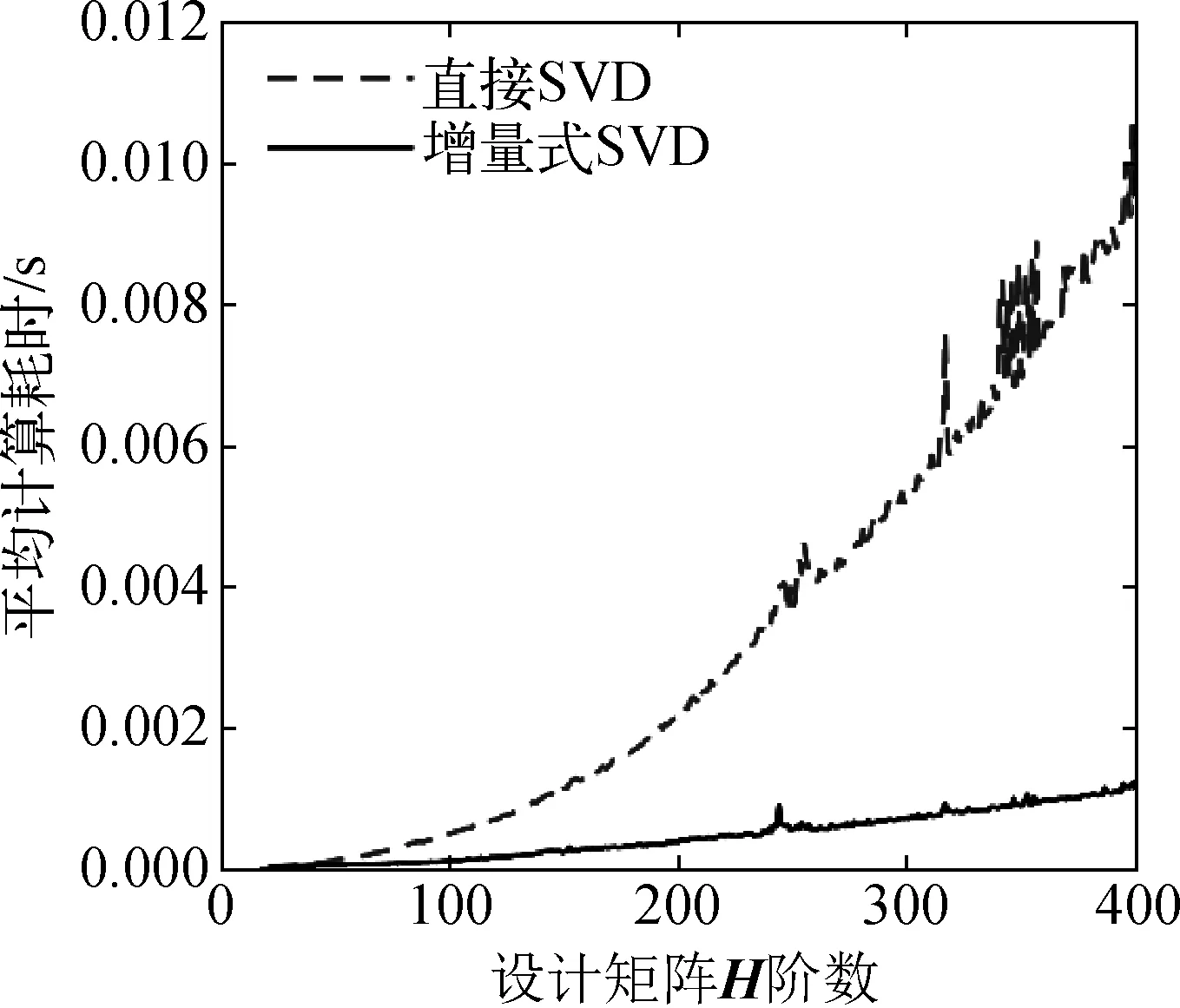
图3 SVD分解耗时对比Fig. 3 Time cost of different SVD method

2 自主寻源算法

第1节的工作能够支持航行器进行在线的信号场拟合，如何规划航行器的航行路径则是本节重点。算法的主体思想实际上是代理优化，通过拟合场的梯度信息进行未知场的探索，首先应该进行拟合场的梯度求解。

2.1 拟合函数梯度求解

由函数之和的求导法则可知，路径点梯度为所有组成函数在该路径点梯度之和：

(22)

已知径向基函数形式，可得径向基函数hj在当前路径点梯度：

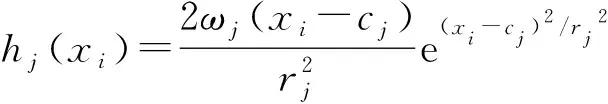
(23)

对式(23)进行求和可以得拟合函数在路径点xi的梯度gi为：

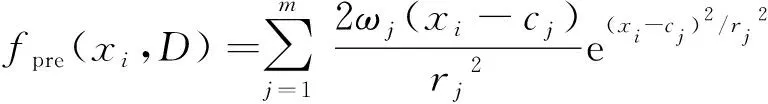
(24)

2.2 脱离局部最优区域

在AUV自主寻优的研究中，航行器陷入局部最优区域是难以避免的问题。类似于遗传算法、模拟退火、粒子群算法等群体智能优化算法可能适用于多航行器的寻优问题，而对于单航行器的寻优问题而言，考虑到航行路径、搜索时间等约束，应用以上群体优化算法是不切实际的。

采用RBFNN对未知分布场进行“拟合估计—最大梯度搜索—重新拟合”的迭代拟合搜索方法，实际上是一种局部邻域搜索算法，相应的存在着拓展算法如禁忌搜索算法和动量梯度算法。禁忌搜索[17]算法的关键思想是通过禁忌表标记已经搜索过的区域并在后续步骤中避免访问，通过限制访问区域来迫使算法接受次优解，并有一定几率访问到局部最优解之外的区域并借此脱离局部最大值区域。该算法的以上特性会导致AUV路径在局部最优区域附近滞留，而且脱离局部区域的路径具有随机性，不适用于文中研究。

动量梯度法作为梯度法的拓展[18]，其算法核心是当前路径点xi并非直接采用梯度方向作为前进方向，而是选择计算所有历史路径点梯度的指数加权平均数作为前进方向。记当前路径点梯度为gi=∇fpre(xi,D)，则求取下一路径点步骤可由式(25)～(26)表示。

(25)

xi+1=xi+hDiri

(26)

其中，μ=0.9为衰减系数，h=10为航行器航行步长，Diri为路径点对应前进方向。

动量梯度算法借鉴了物理学的概念，使得AUV在搜索过程中通过计算梯度指数加权平均数积攒“能量”。其中衰减系数μ起着至关重要的作用，当衰减系数μ=0时，动量梯度法和正常的梯度法相同，当μ=1时，情况类似于无摩擦运动，路径难以在极大值附近收敛。相比于梯度法，动量梯度法具有易于逃脱局部最优区域和更好通过信号场高原区的优点。

2.3 算法流程

文中算法主要内容形成流程如图4所示，首先进行神经网络的初始化：选择出发点坐标，在出发点附近生成一个径向基函数；然后进行流程的循环直至航行器的二维坐标收敛：网络正则化迭代—权重向量计算—当前路径点梯度计算—使用动量梯度法生成航行器下一步的前进方向—获取下一路径点信号值—判定新样本的新颖性并决定是否添加径向基函数。

图4 寻源算法流程Fig. 4 Flow diagram of source-seeking algorithm

3 场源搜索过程模拟计算

3.1 单峰场场源搜索模拟

为验证寻源算法的有效性，模拟了一个热液喷口附近硫化氢浓度的单极值信号场S，如图5(a)所示，该分布场坐标范围为1 000 m×1 000 m，最大值为Smax=25.06 mmol/kg，位于坐标点Pglomax(629,327)。海洋环境中许多信号值随距离增加有极大的衰减[19]，在远离场源的区域信号场梯度较小，文中设计的硫化氢场便具有如此的性质，对该信号场求取梯度，得场梯度分布如图5(b)所示。

图5 单峰硫化氢分布场Fig. 5 Single-peak field of H2S distribution

设置出发点分别为P1(100,100)、P2(100,500)、P3(100,900)、P4(500,900)、P5(900,900)、P6(900,500)、P7(900,100)、P8(500,100)进行寻源过程的模拟计算，为了验证算法稳定性，在真实信号中添加均值为0，方差为0.1的高斯噪声。每次出发点进行1 000次仿真并计算平均路径长度、最大值误差、最大值坐标误差、神经网络的GCV误差及全场均方误差MSE等，计算结果如表1所示。注意到，不同出发点的最大值以及最大值坐标误差基本相同，说明该算法的收敛结果与出发点无关，收敛的精度实际上与航行器的步长相关。径向基函数神经网络无法对远离样本的区域进行准确预测，因此尽管GCV误差仅为0.01的水平，但是全场的均方误差却相对要高。由于神经网络能够对样本区域进行精准地预测，该算法对于信号场路径点上的梯度估计有着误差低于20°的精度，能够为航行器前进方向的计算提供良好基础。

表1 单峰场寻源算法仿真结果Tab. 1 Results of source-seeking simulation in single-peak field

文中将文献[10，20]中的寻源算法进行相同出发点的寻源过程模拟并对比其结果。文献[20]通过控制航行器执行圆形路径机动进行梯度的最小二乘估计并寻找场源。文献[10]方法基于考虑先验场的高斯过程回归(GPR)，进行场源搜索仿真。将3种寻源算法的路径点分布(出发点3)、寻源过程路径长度、路径点梯度估计误差以及GPR方法和RBF方法的全场均方误差MSE进行对比，如图6～9所示。

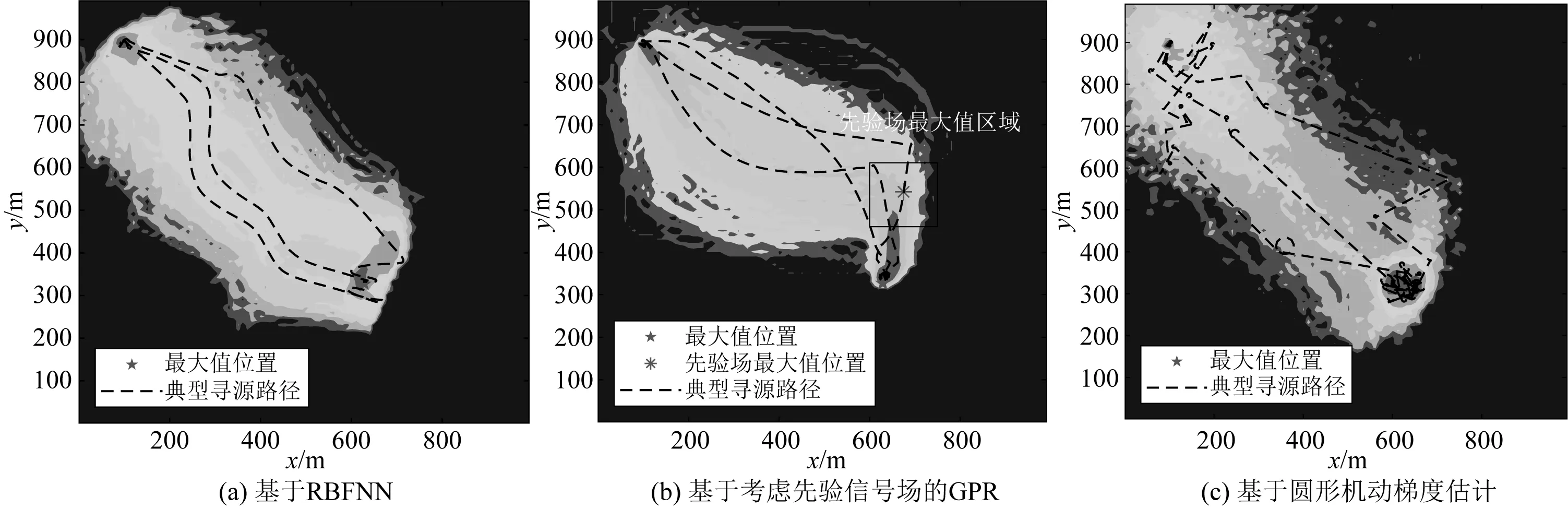
图6 单峰值信号场不同算法寻源过程路径点分布(P3)Fig. 6 Way point distribution of different source-seeking algorithms in single-peak field (P3)

图7 均方误差MSEFig. 7 Mean square error

图8 路径点梯度方向预测误差Fig. 8 Average gradient direction error of track

图9 寻源过程平均路径Fig. 9 Average length of seeking procedure

分析以上数据可以发现，圆形机动估计梯度算法的路径点梯度估计误差最大，GPR算法由于存在先验信号场的影响，梯度估计不如使用无先验信息的RBFNN算法准确，图6中显示基于RBFNN算法产生的路径集中于连接出发点和极值点的直线上，并且由于采用了动量梯度法，其路径往往会在经过极值点后向前延伸一段；GPR算法生成的路径大部分会经过先验信号场的极值区域，这导致其路径相对较长并且均方误差大于基于RBFNN的算法。而基于圆形估计梯度的算法生成的路径散乱，在梯度较小的区域由于信号噪声的存在不能够准确地估计梯度，又由于圆形路径估计梯度的过程存在，其路径远大于其他两个算法。

3.2 多峰场场源搜索模拟

改变原H2S浓度分布场，在原有的H2S浓度分布场S上添加信号场S1：

(27)

该分布场(图10)中局部最大值区域位于Qlocmax(450,750)附近，全局极大值位于Qglomax(629,329)。考虑到本小节旨在测试寻源算法脱离局部最优区域的能力，设计可能陷入局部最大值区域的出发点Q1(200,900)、Q2(300,900)、Q3(400,900)以及Q4(500,900)，对其寻源路径进行多次模拟计算，直至每个出发点的寻源成功率收敛。最后得出不同出发点的平均路径长度、脱离局部最优区域的成功率等数据如表2所示，并绘制出发点1和出发点4的寻源过程路径分布如图11所示。结果显示算法能够以较高的成功率通过局部最大值区域，但是由于局部最大值区域梯度的干扰，AUV的路径可能在该区域弯曲，导致整个寻源过程总路径长度的增加。

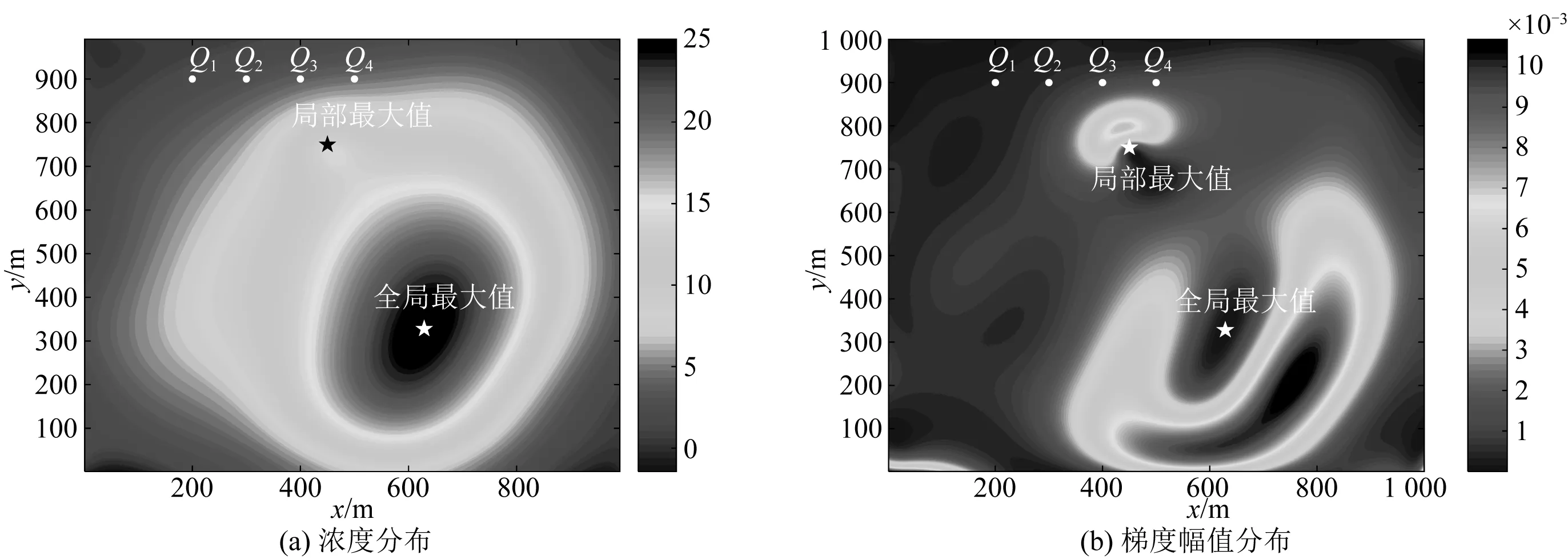
图10 多峰场硫化氢分布场Fig. 10 Multi-peaks field of H2S distribution

图11 多峰值信号场不同出发点寻源路径点分布Fig. 11 Distribution of source seeking way points from different starting points in multi-peak field

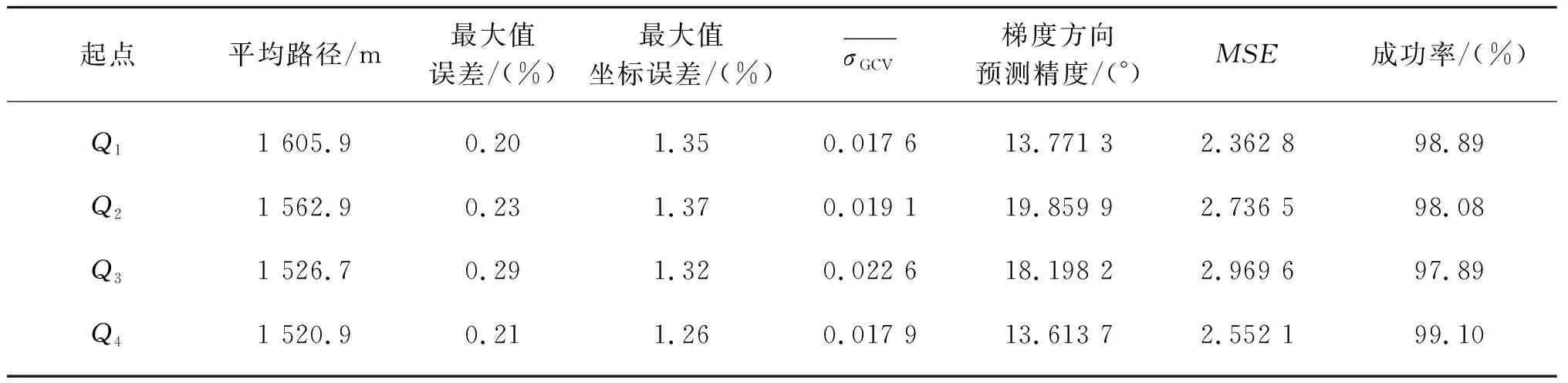
表2 多峰场寻源算法仿真结果Tab. 2 Results of source-seeking simulation in multi-peak field

4 结 语

针对水下航行器在未知环境中的场源搜索问题进行了研究，利用径向基神经网络对未知信号场进行拟合，通过引入正则化参数提高神经网络的泛化性，以广义交叉验证误差为准则优化正则化参数，并以增量式奇异值分解降低正则化参数求解过程的计算复杂度，最后通过拟合场的梯度信息以及动量梯度法规划水下航行器的运动方向。

与其他研究中的寻源算法进行寻源模拟对比发现：文中方法能够对路径点的梯度进行更为准确的估计，从而生成从出发点到场源更短的搜索路径，并且在全场范围内的均方误差更小。此外进行了多峰值信号场的搜索模拟计算，结果显示文中的自主寻源算法能够以较高的成功率脱离局部最优区域。在这里仅考虑单航行器对未知信号场的搜索问题，后续的工作将基于现有的神经网络在线预测算法针对多航行器的协同搜索问题开展。