基于混合优化算法的多UUV协同侦察任务分配方法研究
2021-12-17范学满王新鹏薛昌友
范学满,王新鹏,薛昌友
(1.海军潜艇学院,山东 青岛 266199;2.中国人民解放军92682部队,广东 湛江 524000)
利用搭载传感器载荷的无人潜航器(Unmanned Underwear Vehicle,UUV)执行对海侦察任务是UUV典型的应用方向之一。单个UUV存在巡航时间、载荷数量以及种类等诸多限制,造成其侦察能力有限,往往需要多UUV协同完成对敌方目标的侦察任务。此时,根据任务的复杂度、UUV数量以及任务能力等,对任务进行合理分配,对于提高任务执行效率至关重要[1]。
目前,常用的UUV协同任务分配方法包括合同网法、线性规划法、群体智能法等。文献[2]基于传统合同网算法和蚁群算法,提出一种改进的合同网优化算法,为每个目标函数分配一个蚁群,综合多个优化函数,确定任务分配方案。文献[3]将协同任务分配问题等价于0-1整数线性规划问题,提出一种单编队、多目标时序约束条件下的任务分配模型。文献[4]针对不确定性环境中的任务重分配需求,提出一种滚动时域微分进化量子蜂群优化算法,使得UUV可以根据即时位置和航向等信息,定期或不定期地实现任务重分配。上述算法通常将多UUV的任务分配与航路规划作为两个相对独立的步骤进行分析,通过任务分配确定各UUV的任务集合,随后进行航路规划,确定各UUV的任务执行序列。这种分步策略,虽然降低了任务分配问题的复杂度,但增加了航路规划问题的难度,也在很大程度上导致了以时间最短为目标函数的任务分配方案的次优性。
针对上述问题,本文在多UUV协同侦察任务分配中,显式地考虑任务节点间的距离,利用UUV从母港出发遍历任务节点并返回母港的最短路径,来辅助确定各UUV的任务集合及执行序列,从而将多UUV协同任务分配与单UUV全局路径规划有机融合,有效缓解任务分配与路径规划分离造成的次优性问题。本文研究多UUV、多目标情况下的协同侦察任务分配问题,以遗传算法[5]作为方案寻优的基本框架,在此基础上引入动态规划法[6]解决UUV遍历任务节点时的最短路径问题,即旅行商问题(Traveling Salesman Problem,TSP),综合确定高效合理、负载均衡的任务分配方案。
1 多UUV协同侦察任务分配模型
1.1 模型假设
多UUV协同侦察任务分配问题是一个典型的多约束、多参数的非确定多项式(Non-deterministic Polynomial,NP)问题,该问题涉及系统结构、单体UUV、任务目标和外界环境等多方面因素,考虑不同因素时的模型求解策略有较大不同。本文的基本假设如下:
1)任务目标事先确定,同时环境因素已知且不发生重大变化;
2)任务之间不存在约束关系;
3)每个侦察任务由单个UUV即可完成;
4)执行侦察任务的UUV总数是固定的。
1.2 问题描述
UUV协同侦察任务分配属于团队定向问题(Team Orienteering Problem,TOP)的范畴[7],即在考虑UUV航程、UUV个体数量以及任务时间等限制条件下使收益最大化。TOP问题可以用有向图表示。假设G=(V,A)为完全图,其中,V为节点集,A为边集。V中0号节点对应母港的位置,集合M=V{0}={1,2,…,m}对应目标集。dij为节点i与节点j间的距离(i,j∈V),且dij=dji。ri为完成对目标i的侦察所得的收益,且ri>0(i≠0)。ti为UUV到达目标i后对其完成侦察任务所需的时间。Tmax1、Tmax2分别为协同侦察任务的时间上限和最长UUV续航时间,如果一个UUV到达目标i,且任务剩余时间或续航剩余时间小于ti,则该UUV不能获得收益ri。
假设K为UUV集合,综合考虑所需UUV数量和协同完成侦察任务所需总时间,设置两个优化目标:其一是使用于侦察的UUV数量尽可能少,其二是使任务完成时间尽可能短。由此,可得多目标优化问题:

(1)
式中,yik为布尔变量,当UUVk负责侦察目标i时,取值为1,反之为0;xijk为布尔变量,当UUVk的航路经由边(i,j)时,取值为1,反之为0;sk为UUV的航速;|K|为可用于侦察的UUV总数目;N表示实际用于执行侦察任务的UUV数量,N≤|K|;T为多UUV协同完成侦察任务的时间,即参与侦察UUV任务执行时间的最大值:
T=max{T1,T2,…,Tk,…,TN}
(2)
式中,Tk为UUVk完成侦察任务的时间。
通过求解式(1),可以确定实际用于侦察的UUV数量N,以及每个UUV的任务子集
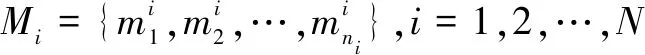
(3)
式中,ni为UUVi需要执行的任务个数。
对于上述多目标优化问题,使用的UUV数量尽可能少与任务完成时间尽可能短之间存在冲突,通常不能同时达到最优,所以,最优解不一定只有一个,这样的最优解称为Pareto最优解或“非支配解”,所有Pareto最优解构成的集合称为Pareto前沿[8]。
2 基于混合优化算法的任务分配方法
多UUV协同侦察任务分配是一个多目标优化问题,可以利用遗传算法、差分进化算法、粒子群算法等进化算法进行解决[9]。对于遗传算法,目前具有代表性的多目标优化遗传算法有帕累托排序法、非支配排序法、多目标函数加权以及基于参考点的多目标进化算法等。本文选择经典的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ,NSGA-Ⅱ)进行优化。
对于同一任务子集,执行顺序不同,收益和代价会有显著不同,因此,将任务规划划分为任务分配与路径规划两个相对独立的阶段,通过任务分配确定任务子集,在此基础上,通过路径规划确定执行顺序,极易造成总体任务规划方案的次优性问题[10]。为了有效解决这一问题,将航路规划的部分操作前移,在任务分配阶段考虑任务执行顺序对任务执行时间的影响。出于效率的考虑,本文选择动态规划算法用于任务子集执行顺序的优化。
综上所述,本文将NSGA-Ⅱ与动态规划算法相结合,以NSGA-Ⅱ作为基本框架用于求解多目标优化问题,将动态规划算法嵌入NSGA-Ⅱ框架中,用于优化确定任务子集的执行顺序,基于优化后的执行顺序计算相应任务子集的收益和代价。可得混合优化算法的流程如图1所示。

图1 混合优化算法流程
2.1 基于动态规划的TSP问题求解
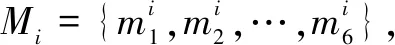
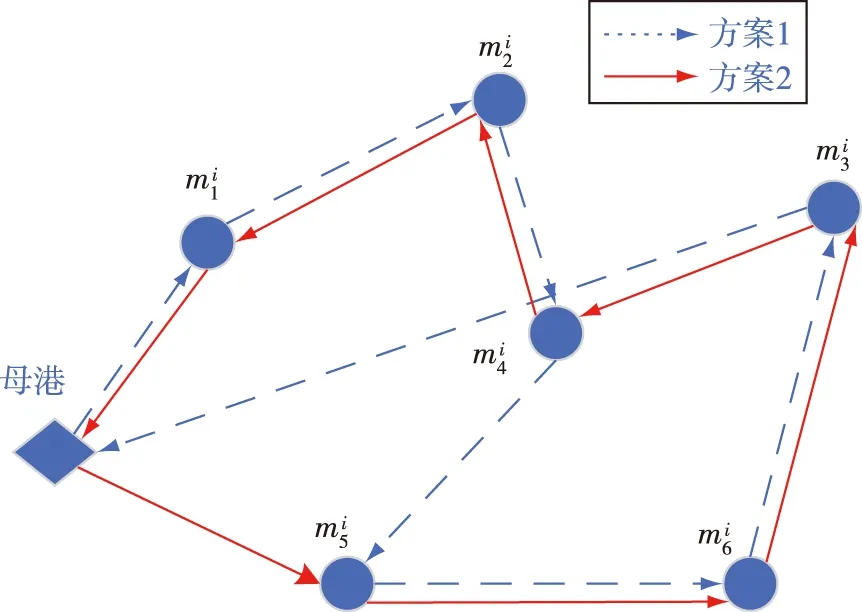
图2 TSP问题示意图
动态规划法是求解多阶段决策最优化问题的技术之一,其基本思想是把复杂的多阶段决策问题划分为多个易于解决的子问题,每个子问题对应决策过程的一个阶段。通常,划分所得的子问题之间有一定重叠。动态规划法在求得子问题的解后,会记录在表中,后续用到子问题解时,只需查表即可,无须重复计算,从而避免了大量重复计算,提升了寻优效率[11]。图3给出了动态规划法的求解过程。
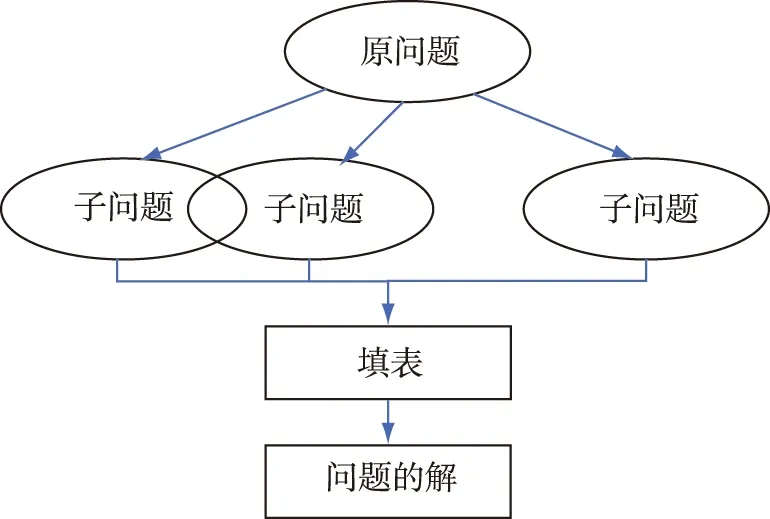
图3 动态规划法的求解过程
对于单个UUV,其任务点和母港构成节点集V,节点间的两两连线构成边集E,可用图G=(V,E)表示。d(s,V′)表示从母港s出发,经所有任务节点V′=V-{s}一次且只有一次,最后返回母港s的最短路径长度,则动态规划函数为
d(s,V′)=min{cks+d(k,V′-{k})},k∈V′
(4)
式中,cks为节点k到s的路径长度:
cks=d(k,s),k≠s
(5)
通过动态规划进行优化,可以得到每个UUV任务子集的任务执行序列,该任务序列将作为NSGA-Ⅱ的种群个体参与多UUV任务分配的进化寻优。
2.2 NSGA-Ⅱ优化框架
NSGA-Ⅱ算法的基本思想为:首先,进行种群的随机初始化,非支配排序后通过选择、交叉、变异等进化操作得到第一代子代种群;然后,从第二代开始,将合并父代与子代种群,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群;最后,通过遗传进化操作产生新的子代种群;依此类推,直到满足终止条件为止[12]。
本文将种群染色体表示为二维矩阵,记为
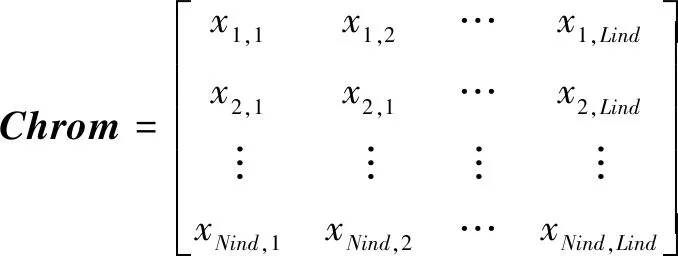
(6)
式中,Nind为种群的规模,即种群的个体数;Lind为种群个体的染色体长度,此处Lind=|M|,即待侦察目标总数。
Chrom中每行对应一个个体的染色体,个体染色体采用“整数编码”方式,对于Chrom中的任一个体可表示为如下行向量
Chromi=(xi,1,xi,2,…,xi,Lind),i=1,2,…,Nind
(7)
式中,xi,j∈{1,2,…,|K|},j=1,2,…,Lind,表示目标j分配给UUVi进行侦察。Chromi则对应多UUV协同侦察任务分配的一个方案,如图4所示。
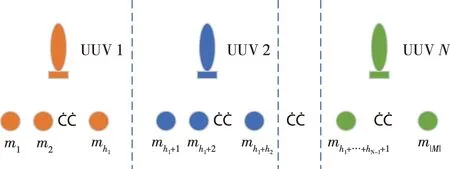
图4 协同任务分配方案
图4中,N≤|K|,即可能只需要使用部分UUV即可完成协同侦察任务;{m1,m2,…,mh1}为分配给UUV 1的任务子集,不同UUV的任务子集的交集为空。
由式(1)可知,式(6)所示的种群矩阵对应一个二元目标函数值矩阵:
(8)
式中,f1(·)=N、f2(·)=T分别对应两个最小化优化目标;每行对应Chrom中相应个体的目标函数值。
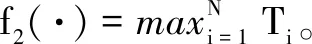
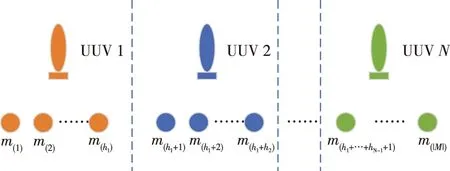
图5 协同任务分配方案(动态规划优化后)
本文将动态规划的寻优结果纳入NSGA-Ⅱ优化框架,只需要在进行快速非支配排序前,利用动态规划算法进行任务子集的TSP寻优,在寻优所得的任务序列上计算目标函数值,然后,进行非支配排序即可。改进后的NSGA-Ⅱ如图6所示。

图6 改进后的NSGA-Ⅱ算法流程
通过将动态规划嵌入NSGA-Ⅱ优化框架中,可以利用动态规划法优化得到的任务执行序列作为启发信息,减小NSGA-Ⅱ的搜索宽度,增大NSGA-Ⅱ的搜索深度,有效提升NSGA-Ⅱ优化效率。
3 实验分析
假设共有7个可用于侦察的UUV,UUV的航速为8 kn,所有UUV均从同一母港出发。待侦察区域为20 nmile×20 nmile的正方形区域,其中,随机分布40个待侦察目标,想定场景如图7所示。图中,“■”表示UUV母港,“●”表示待侦察目标。

图7 想定场景示意图
为了验证混合优化算法的可行性,将经典NSGA-Ⅱ算法作为基线算法。对于混合算法和经典NSGA-Ⅱ算法,均设置种群规模Nind=100,进化代数maxGen=200,变异算子的变异概率Pm=0.3,交叉算子的交叉概率Pr=0.9。软件方面,使用Python开源进化算法工具箱Geatpy2[13]进行算法开发;硬件配置为:Intel(R)_Core(TM)_i7-6700HQ CPU,主频2.60 GHz,内存16 GB。
3.1 混合优化算法结果分析
混合优化算法得到的Pareto非支配解集中共95个解,对应的Pareto前沿如图8所示。

图8 混合优化算法的Pareto前沿
由图8可知,95个非支配解在两个优化目标上大多数是重合的,因此,在图上融合为两个点。实际应用中,可以根据任务需求和偏好任选一个方案。当然,出于节省能源考虑,可以将各UUV航行距离之和尽可能小作为方案进一步优选的依据。95个非支配解对应的总航行距离如图9所示。

图9 混合优化算法各方案的UUV总航行距离
由图9可见,各方案在总航行距离这一指标上有较大差异,95个方案中最小总航程为220.13 nmile,对应72号方案;最大总航程为258.57 nmile,对应75号方案。另外,72号方案对应的UUV数目为6,任务完成时间为4.85 h;75号方案对应的UUV数目为7,任务完成时间为4.83 h。72号方案在减少出动1个UUV的基础上,进一步缩短了总航程,因此,在任务不紧迫的情况下推荐使用72号方案,其对应的任务分配结果如图10所示。
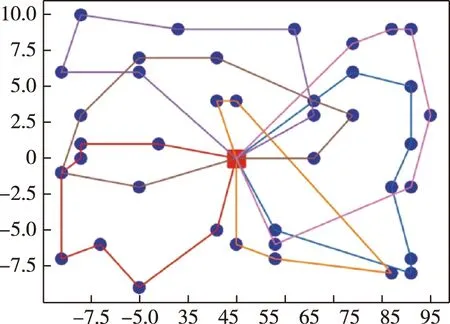
图10 混合优化算法的任务分配方案
3.2 NSGA-Ⅱ算法结果分析
NSGA-Ⅱ算法得到的Pareto非支配解集中共9个解,对应的Pareto前沿如图11所示。可见,9个解重叠为3个前沿点,与图8对比可知,无论实际使用几个UUV,任务完成时间均长于混合算法得到的方案。

图11 NSGA-Ⅱ算法的Pareto前沿
9个非支配解对应的总航行距离如图12所示。
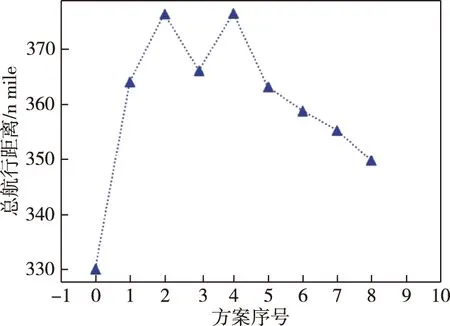
图12 各方案的UUV总航行距离
由图12可见,各方案在总航行距离这一指标上有较大差异,0号方案总航程最小,为330.07 nmile;4号方案总航程最大,为376.48 nmile。即便是最小航程也明显大于混合优化算法的最长航程。下面给出任务完成时间最短方案(0号方案)的任务分配结果如图13所示。
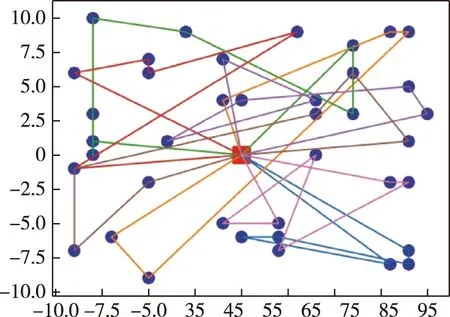
图13 NSGA-Ⅱ算法的任务分配方案
对比图10与图13可知,图13的任务分配方案中存在大量往复、折返航行的情况,从而导致浪费大量航程和任务时间。而混合优化算法通过利用动态规划优化任务序列,有效缓解了上述问题,提升了任务分配方案的合理性。
4 结束语
为了提升多UUV协同侦察静态任务规划方案的整体最优性,将航路规划的部分工作前移至静态任务分配阶段,使得任务分配在为各UUV指派任务子集的基础上,还能给出具有一定参考价值的任务执行序列。基于上述思想,将动态规划法嵌入NSGA-Ⅱ的进化框架,提出一种混合优化算法,该算法能够在兼顾UUV数目和任务完成时间的基础上,给出总航程更优的任务执行序列。在典型场景下进行仿真对比实验,实验结果表明:在任务分配过程中显式地考虑任务执行顺序对方案性能的影响,能够提升寻优方案的质量。后续将在此基础上,考虑多约束条件、多优化目标等复杂情况,进行更深入的研究。
