某大楼在撞击荷载下的抗连续倒塌分析

摘  要：本文运用有限元模型，采用直接去柱和撞击去柱两种方法，模拟俄亥俄州立大学综合大楼拆除底层中柱的过程，对俄亥俄州立大学综合大楼的抗连续倒塌机制进行了分析，从而证明多层框架结构简化模型的合理性。通过对直接去柱法和撞击去柱法的对比，结果表明：用直接去柱法拆除中柱后，经过一段时间振荡最后达到平衡;而用撞击去柱法拆除中柱后，撞击点及正上方节点受到较大破坏。由此得知，抗連续倒塌研究应该结合具体灾害进一步分析，避免直接去柱法低估灾害对结构的影响。

关键词：有限元模型;直接去除法;撞击去柱法

中图分类号：TU393 文献标识码：A

0引言

结构连续倒塌是指结构受到意外荷载作用后产生局部破坏并向其他单元扩展，最终导致结构整体或大范围区域的倒塌[1]。引起连续性倒塌破坏的原因多种多样，抗连续性倒塌模拟实验却经常抛开倒塌破坏原因，采用直接拆除关键柱的方法，研究剩余结构在重力荷载下抗倒塌机制[2]。而与直接拆除关键柱导致的结构倒塌相比，人为破坏和具体灾害除了导致的结构关键柱的破坏，还会对关键柱周围的结构产生一定的损害，建筑结构连续性倒塌的特性、破坏方式、受力方式等都会有所差别（比如：汽车撞击）。这样的模拟实验忽略了人为破坏和具体灾害对结构周围的破坏影响，并不能很客观的反映出建筑结构的实际情况，达不到理想的实验效果。

本文在已有试验的基础上，通过有限元模型，采用了直接去柱法和撞击去柱法，利用模拟俄亥俄州立大学综合大楼[3]拆除底层中柱的过程，对具体灾害导致建筑结构连续倒塌和直接拆除关键柱导致结构倒塌两种实验结果进行了对比，得出具体灾害对结构的破坏更严重这样的结果。

1直接去柱法有限元模型

俄亥俄州立大学综合大楼（the Ohio Union building），位于美国俄亥俄州首府哥伦布市的俄亥俄州立大学校园内，如图1，大楼建成于1951年，在2007年达到使用年限，song对该大楼进行了原位拆除试验，分析整体结构的抗倒塌性能。本文采用ABAQUS软件建立俄亥俄州立大学综合大楼的有限元模型，模型包括大楼的地下室，如图2。模型的梁采用0.2m，梁柱节点采用刚性连接，材料损伤采用Yu和Jeong提出的由应力三轴度确定的柔性损伤准则[4]。加载过程中将墙、楼板等组成的恒载换算成框架梁的密度。由于框架柱的拆除时间会影响最后的分析结果，在直接去除法中，为了符合瞬时拆除柱的假设，拆柱时间小于剩余结构第1阶竖向自振周期的1/10，结合模态分析可知第1阶竖向自振周期是0.489秒，故拆柱时间设为0.01秒。

2撞击去柱法有限元模型

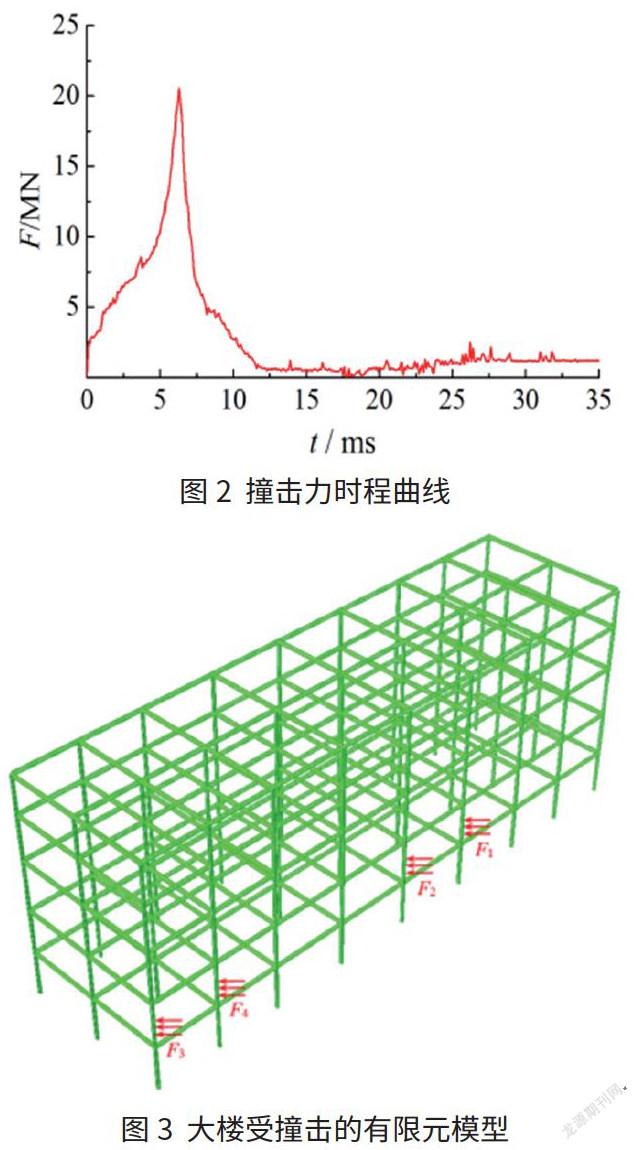
在撞击去柱法有限元模型的建立中，撞击结构过程持时较短，一般在0.2s内结束[5]，故采用爆炸荷载常用的施加方法，首先计算撞击受压柱的撞击力时程曲线，然后再将撞击力时程曲线依次施加到被拆柱。利用ABAQUS软件的显式动力分析法，考虑材料损伤和应变率的影响，将载重8t的汽车以72km/h的速度撞击框架柱，撞击力时程曲线如图3所示。时程曲线中的最大撞击力发生在前15ms，故将t=0～15ms的撞击力时程曲线依次叠加到被拆柱。如图4所示，分别对柱1、2、3、4的中下部施加撞击力荷载，当撞击力达到峰值时，柱被撞断。在撞击下一根柱前，剩余结构留有0.505s自由振动。施加荷载的时间分别为：（1）t=0～0.05s：施加结构自重等荷载;（2）t=0.05～0.065s：柱1施加撞击力荷载F1;（3）t=0.57～0.585s：柱2施加撞击力荷载F2;（4）t=1.09～1.105s：柱3施加撞击力荷载F3;（5）t=1.61～1.625s：柱4施加撞击力荷载F4。

3直接去柱法和间接去柱法的模拟结果及其对比

多层平面框架结构的中柱失效后，各层表现出不同的抗倒塌机制，由梁机制、悬链线机制、空腹机制抵抗不平衡荷载。中柱失效后，失效跨各层梁的轴力分布不同，顶层梁为压弯构件，底层梁为拉弯构件;本文主要讨论第一根柱失效后的受力特性。

3.1 直接去柱法

柱1失效后，节点1的位移在t=0.1s达到第一个位移峰值，峰值时刻的变形图如图4所示，剩余结构失效跨各层梁的梁端弯矩时程曲线，如图5所示。经过对比发现，弯矩在第一个位移峰值时刻有如下规律：在失效跨，各层梁的梁端弯矩值接近，第1层到第4层的弯矩值分别为650kN·m、649kN·m、638kN·m、597kN·m，主要通过梁机制抵抗连续倒塌。

柱1失效后，节点1正上方的剩余柱退出工作，竖向荷载通过失效跨的梁转移到相邻结构。各层梁的轴力差别较大。顶层梁和底层梁的轴力最大，且正负相反，而中间层相对较小;失效跨的轴力大于其它跨，这点与弯矩有着相同的规律。选取失效跨各层梁的轴力时程曲线，如图6所示，第4层的轴力为压力，在数值上大于第1、2、3层梁的轴力。

3.2 撞击去柱法

柱1被撞断后，节点1达到第一个位移峰值时刻的弯矩最大值发生在柱1右侧失效跨，变形图如图7所示，最大弯矩值为890kN·m，大于直接去柱法的最大弯矩值650 kN·m。该大楼框架梁的极限受弯承载力为914.94 kN·m，失效跨最大弯矩值接近受弯承载力，说明撞击去柱法对构件的破坏大于直接去柱的破坏。取失效跨各层梁的梁端弯矩时程曲线，如图8所示，在峰值时刻，从第1层到第4层分别为886kN·m、856kN·m、821kN·m和744kN·m，进入稳定阶段后，第3、4层的弯矩值大于第1、2层，这是由于靠近撞击位置的构件在撞击过程中发生损伤。

在撞击柱1结束后第一个位移峰值时刻的轴力，在第1层为拉力，但失效柱左右两侧拉力值不同，左侧为220kN，右侧为64kN。图9为柱1左侧失效跨各层梁的轴力时程曲线，撞击过程中第1层的轴力超过800kN，撞击结束后第1个位移峰值时刻，第1层到第4层的轴力分别为220kN、63kN、-51kN、-170kN。

4结论

本文分别采用了直接去除法和撞击去除法通过有限元模型，对建筑结构的连续抗倒塌机制进行了分析，对两种方法所创建的有限元模型进行了对比，通过观察节点位移时程曲线。得出以下结论：（1）撞击拆除法不仅能使结构关键柱失效，还对关键柱周围结构环境造成损伤。（2）直接去除法虽然能够间接反映出结构的抗倒塌机制，但是，却不能够完全体现出具体灾害对结构的影响。因此，在我们分析自然灾害和人为灾害对建筑结构破坏时，要结合具体灾害来研究结构的抗倒塌性能。

参考文献

[1]ASCE7-0.5 Minimum design loads for buildings and other structues[S].Virginia： American Society of Civil Engineers，2006.

[2]易伟建，何庆锋，肖岩.钢筋混凝土框架结构抗倒塌性能的试验研究[J].建筑结构学报，2007，28（5）：104-109.

[3]Song B I， Sezen H. Experimental and analytical progressive collapse assessment of a steel frame building [J]. Engineering Structures，2013，56：664-672.

[4]Yu H L， Jeong D Y. Application of a stress triaxiality dependent fracture criterion in the finite element analysis of unnotched charpy specimens [J].Theoretical and Applied Fracture Mechanics，2010，54（1）：54−62.

[5]崔堃鹏，夏禾，夏超逸，等.汽车撞击桥墩瞬态撞击力的等效静力计算[J].振动与冲击，2014，33（4）：48-53.

收稿日期：2021-08-05

作者简介：乔惠云（1981—），女，山西临汾人，博士，讲师，研究方向：钢结构抗连续倒塌。