各向异性ruby 晶格中费米子体系的Mott 相变*
2021-12-16保安
保安
(南昌工学院教育学院,南昌 330108)
本文用哈伯德模型研究各向异性ruby 晶格中费米子行为,在团簇动力学平均场理论框架内将格点模型映射为有效自洽场中的杂质模型后用连续-时间量子蒙特卡罗算法求解杂质模型.基于自洽计算的结果,用最大熵方法得到各向异性ruby 晶格中具有相互作用的费米子体系的单粒子态密度和双占据数后讨论了温度(T)、相互作用(U)和各向异性参数(λ)对体系的金属-绝缘相变的影响.最后给出各向异性ruby 晶格中费米子体系的温度-相互作用相图,研究结果表明,低温和弱相互作用范围体系处在金属相,而在高温和强相互作用下体系内出现Mott 绝缘体相.
1 引言
研究和发现二维强关联体系的拓扑绝缘体、量子霍尔效应、量子反常霍尔效应、玻色-爱因斯坦凝聚等新奇物相是凝聚态物理的重要内容[1-7].拓扑绝缘体材料Bi14Rh3I9[8]的某一特定平面内存在的二维ruby 晶格,由于独特的晶格结构而引起研究人员兴趣.拓扑绝缘体材料Bi14Rh3I9的晶体结构中有周期性交错堆垛的铋-铑网格和绝缘层(图1(a)—(c));由共棱RhBi8立方体覆盖六角晶格边所形成的金属间化合物的某一特定平面构成二维ruby 晶格(图1(d)).

图1 拓扑绝缘体材料Bi14Rh3I9的晶格结构示意图 (a)-(c) Bi14Rh3I9 的晶体结构及其构成单元,绝缘层的zigzag 链分离由共棱RhBi8立方体构成的六角网格状金属间的 [(Rh4Bi)3I]2+层,六角晶格的边由共棱RhBi8立方体覆盖;(d) 二维ruby 晶格与六角晶格结构俯视图[8]Fig.1.Sketch of crystal structure of topological insulator Bi14Rh3I9:(a)-(c) Triclinic crystal structure of Bi14Rh3I9.Insulating layers of [Bi2I8]2— zigzag chains separate the intermetallic [(RhBi4)3I]2+ layers that consist of hexagonal nets of edge-sharing RhBi8cubes;(d) honeycomb lattice of graphene with the structure of the intermetallic layer [8].
研究人员开展了诸多有关ruby 晶格的研究工作并得到了丰富的成果.文献[9,10]介绍了用二维Ising 模型描述ruby 晶格和ruby 晶格上二维冰剩余熵的研究.近期研究人员在考虑自旋-轨道耦合效应的情况下用紧束缚模型或哈伯德模型研究二维ruby 晶格后发现了拓扑绝缘体、分数量子霍尔效应和量子自旋液体等更为丰富的结果[11-14].除此之外,用Kitaev 模型研究二维ruby 晶格后发现了拓扑自旋液体相等的有趣结果[15,16].然而,目前为止还没有研究工作讨论各向异性ruby 晶格中费米子间的在位相互作用和温度对该体系量子相变的影响.
本文以半满的单带哈伯德模型描述各向异性ruby 晶格中具有在位相互作用的费米子行为,结合团簇动力学平均场理论和连续-时间量子蒙特卡罗方法求解杂质模型.
2 理论模型与研究方法
2.1 理论模型
二维ruby 晶格是类六角晶格,其结构相当于将六角晶格的顶点用三角晶格替换,六角晶格的棱则用平方格子替换,如图2(a)所示.用哈伯德模型[17-21]描述各向异性ruby 晶格中具有在位相互作用的费米子行为的哈密顿量为

图2 (a) Ruby 晶格结构示意图;(b) ruby 晶格第一布里渊区;(c) 各向异性ruby 晶格(λ=2.0)中费米子体系T=0.2和U=0时的态密度;(d) 各向异性ruby 晶格(λ=2.0)中费米子体系无相互作用情况下色散关系Fig.2.(a) Sketch of ruby lattice;(b) first Brillouin zone of ruby lattice;(c) density of states of anisotropic ruby lattice (λ=2.0)for T=0.2,U=0;(d) energy dispersion of anisotropic ruby lattice (λ=2.0) for T=0.2,U=0.
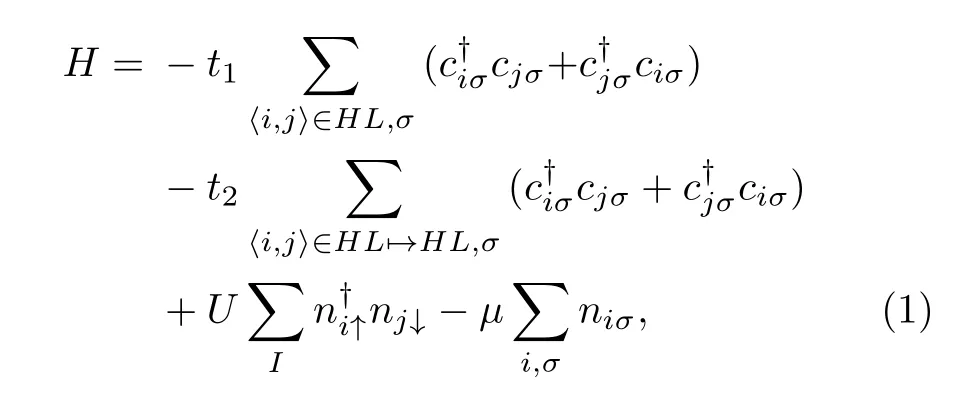
其中,和cjσ分别表示i格点上自旋为σ 的粒子生成算符和j格点上自旋为σ 的费米子湮灭算符,niσ是粒子数算符,σ 是自旋指标,其值为↑或↓.t1和t2分别代表同一个六角晶格(HL)内最近邻格点之间的跃迁和紧邻两个六角晶格的最近邻格点之间的跃迁.〈i,j〉∈HL表示同一个六角晶格内所有最近邻格点,〈i,j〉∈HL→HL表示紧邻两个六角晶格之间所有最近邻的格点.U是在位相互作用,µ是化学势.计算中定义各向异性参数λ=t1/t2并选定t1=1 来讨论ruby 晶格的各向异性程度对体系量子相变的影响.
2.2 研究方法
在解析求解描述强关联体系的Ising 模型、Heisenberg 模型、t-J模型和哈伯德模型等理论模型时遇到了极大的挑战,即便处理简单的哈伯德模型和Kondo 晶格模型的时候也遇到了困难.随着计算机数据处理能力的提高和储存空间的扩大,精确对角化[22,23]、蒙特卡罗方法[24,25]、Lanczos 方法[26]及重整化群[27,28]等数值计算方法被应用在强关联体系的研究中并给出了令人满意的结果,但以上数值计算方法各有其不足之处.相比上述数值计算方法,动力学平均场理论在强关联体系的研究中因给出更加令人满意的结果而得到了研究人员的青睐.动力学平均场理论的建立与发展为强关联电子体系的研究开辟了新的途径,主要成果有反铁磁金属到反铁磁绝缘体相变的动力学平均场理论、铜氧化物中反铁磁和d 波高温超导的团簇动力学理论研究、六角晶格上半满哈伯德模型Mott 相变、一维扩展哈伯德模型量子相变的团簇动力学平均场理论研究等[29-35].

式中,i,j是团簇的序号(此处将所选团簇序号标为j=0),µ,υ是每个团簇内格点的指标,Sc包含团簇内的所有项的作用量,Sb包括所选团簇之外所有项的作用量,Sbc则包含连接团簇和其所处自洽场的所有项的作用量.做如下两个假设:1) 所有超过团簇大小的相互作用不考虑;2) 有效作用量中不考虑四次或更高阶的重整化.通过计算在j/=0的所有变量上的路径积分,可以获得只包含所选团簇变量的(团簇自由度的)有效作用量:

以方格子为例,进一步说明动力学平均场理论将格点模型映射到有效自洽场杂质模型的基本思想.对图3所示的 2×2 的超级晶格,其团簇自能是4×4的矩阵,K是超级晶格的简约布里渊区,I表示 4×4 的单位矩阵,µ为化学势.t(K)是超级晶格的跃迁矩阵,保留团簇内部的指标,其矩阵元为

图3 方晶格模型映射到有效自洽场杂质模型的示意图 (a) 方晶格;(b) 具有四个格点的超级晶格;(c)有效自洽场中团簇杂质模型的示意图Fig.3.Sketch of mapping square lattice model to impurity model in self-consistent field:(a) Square lattice;(b) sketch of supper lattice consists of 4 lattice point;(c) sketch of cluster impurity in self-consistent field.

r1和r2是超晶格基矢,i,j为团簇内部格点的指标.
将格点模型映射到有效自洽场中杂质模型后需要用杂质求解器解杂质模型.本工作选用的连续-时间量子蒙特卡罗算法[37-40]对具有非局域影响和相互作用依赖时间的体系是有效的和可行的杂质求解器.连续-时间量子蒙特卡罗方法在随机变量及其分布的计算中所用到的主要数学基础包括Metropolis 重要抽样、大数定理和中心极限定理.以本论文所涉及的“用半满的单带哈伯德模型描述各向异性ruby 晶格中费米子体系的哈密顿量”为例介绍连续-时间量子蒙特卡罗算法.

其中H0和H1分别为相互作用绘景中不含时间的部分和微扰的部分.相互作用U=0 时,ruby晶格的哈伯德模型转变为紧束缚模型的哈密顿量,其哈密顿量在动量空间中的表达式则变为其中

对作用量级数展开后体系的配分函数形式如下:

其中Tr 是求矩阵迹的符号,Tτ为编时算符.在不引起误解的情况下,将(8)式中时间指标、空间指标和级数展开指标可以简化为κ ≡{k,i,{τi}},则体系配分函数可写为如下形式:

暂且假定(9)式中被积函数均为正,其中Z0=Tr exp(-βH0).使用维克定理可使配分函数中的被积函数简化,且任意可观测量O的平均值为
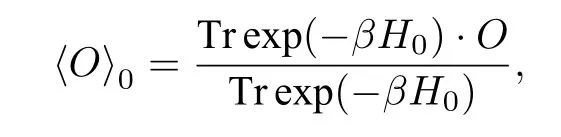
因此被积函数中自旋向上部分的期望值为(以κ=3的随机行走为例,如图4所示):

图4 κ=3 时一个随机行走示意图Fig.4.Sketch of random walk for κ=3.

G0(i,j)为相互作用大小等于0 的情况下体系的格林函数.自旋向下部分的期望值同理可得.
对于κ阶的情况,

自旋向下部分的期望值同理可得.
随机行走的过程中需要考虑减顶点和加顶点两种情况.Metropolis 重要抽样算法的细致平衡条件为:

增加一个顶点的Metropolis 重要抽样的接收率为

具体计算中在0 到1 的区间取均匀分布的随机数,直到随机数小于R方可结束随机行走.减顶点和加顶点概率的计算中对行列式比值的计算非常重要.在已有的κ顶点增加一个顶点时,快速计算的方法如下:

从已有的κ+1 个顶点减去一个顶点的概率为



结合团簇动力学平均场理论和连续-时间量子蒙特卡罗算法进行数值计算的流程如下.
1) 利用微扰论给出一个小的初始团簇自由能.
2) 利用杂质求解器,如:连续-时间量子蒙特卡罗算法进行求解,得到团簇的格林函数.
3) 对团簇格林函数做一次傅里叶变换.
4) 利用Dyson 方程

循环运行上述计算步骤直到前后两个自能的差值达到所要精度求方可结束自洽计算,自洽计算的具体流程可见图5.
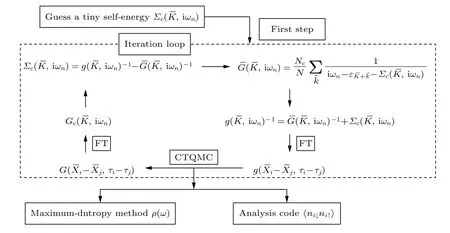
图5 自洽计算的流程图Fig.5.Flow chart of self-consistent calculation.
3 计算结果
态密度(density of state)和双占据数(double occupancy)是二维强关联体系Mott 转变研究中的两个重要参数.本文用连续-时间量子蒙特卡罗方法求解自洽场中的杂质模型,从虚时格林函数G(τ)出发,用最大熵方法[39]计算得到各向异性ruby 晶格中费米子体系的态密度
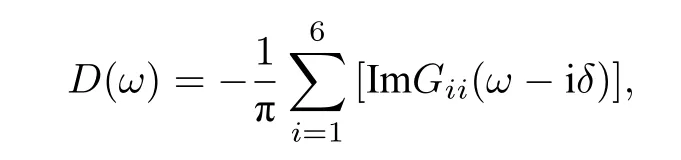
其中i是用团簇动力学平均场理论将格点模型映射到自洽场中杂质模型后的团簇内格点的序号.
首先给出各向异性ruby 晶格(λ=2.0)中费米子体系的固定温度(T=0.2)情况下对应不同相互作用的态密度(图6(a))和固定相互作用(U=8.0)情况下对应不同温度的态密度(图6(b)).之后比较了温度(T=0.2)和相互作用(U=8.0)都固定的情况下对应不同各向异性参数λ的态密度的演化(图7).

图6 各向异性ruby 晶格(λ=2.0)中费米子体系的态密度 (a) T=0.2 时不同相互作用对应的态密度;(b) U=8 时不同温度对应的态密度Fig.6.Density of states of anisotropic ruby lattice (λ=2.0)with fermions:(a) Density of states for different interaction at T=0.2 ;(b) density of states for different temperature at U=8.0.
如图7所示,温度T=0.2和相互作用U=8.0的情况下,随着各向异性参数λ的增大费米面两侧态密度谱峰逐渐演化到最后在λ≈1 时费米面处出现能隙.λ=2和λ=0.67 时态密度的演化形式类似,不出现近藤峰.λ=1 态密度演化过程中出现准粒子峰,即近藤峰,其特征是松原频率ω=0 处两侧出现具有类似肩膀的准粒子峰.由态密度演化形式可以推测,在λ=2到λ=1 的过程中,体系中会出现近藤金属.各向异性参数对态密度的演化发现和赝能隙的形成具有显著的影响.在固定的排斥相互作用能情况下,通过比较不同各向异性参数所对应的态密度发现,松原频率ω=0 处态密度随着各向异性参数的增大而减小.严格来说,在有限温度下由ω=0 处态密度的赝能隙决定的相变,实际上是一个转变(crossover).
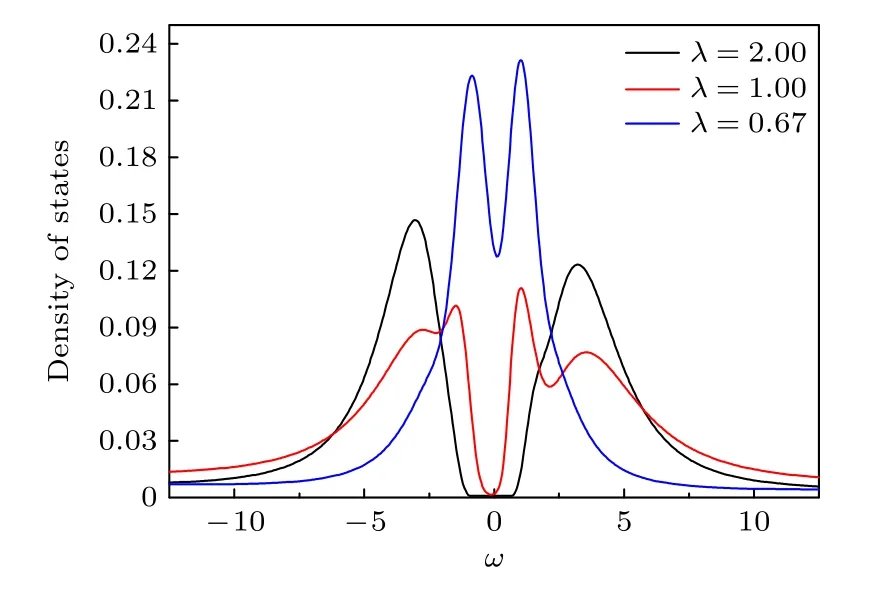
图7 固定温度(T=0.2)和固定相互作用(U=8.0)情况下,各向异性参数对ruby 晶格中费米子体系态密度的影响Fig.7.Comparison of the effect of anisotropic parameter λ on the density of states of fermions in ruby lattice on for T=2and U=0.
双占据数是用半满的哈伯德模型描述强关联体系金属-绝缘相变的另一个重要参数.双占据数定义为 Docc=∂F/∂U=,其中F是自由能,U是相互作用.图8(a),(b)分别给出不同相互作用情况下各向异性ruby 晶格(λ=2)的双占据数随温度的变化和不同温度情况下各向异性ruby 晶格(λ=2)的双占据数随相互作用的变化.如图8(a)所示,随着温度的降低,温度对于双占据数的影响趋于不明显.由图8(b)可知,随着相互作用的增加体系的双占据数趋于0,意味着费米子的局域化程度增强.

图8 各向异性ruby 晶格中费米子体系的双占据数 (a) 不同相互作用下体系双占据数随温度的变化;(b) 不同温度下体系双占据数随相互作用的变化Fig.8.Double occupancy of anisotropic ruby lattice with fermions:(a) Comparison between double occupancy for different temperature with the change of interaction;(b) comparison between double occupancy for different interaction with the change of temperature.
图9所示为各向异性参数对体系双占据数的影响.在固定温度(T=0.2)和固定相互作用(T=8.0)情况下,ruby 晶格中费米子体系的双占据数随着各向异性参数的增大趋于0,这一趋势说明费米子局域化加强,即体系趋于Mott 绝缘体相,但趋势放缓.

图9 温度和相互作用固定的情况下,ruby 晶格中费米子体系的双占据数随各向异性参数的变化Fig.9.Trend of double occupancy with the change of anisotropic parameter for fixed T and U.
最后,基于体系的态密度和双占据数,给出了体现温度和相互作用对各向异性ruby 晶格(λ=2.0)中相互作用费米子体系金属-绝缘相变的影响,即温度-相互作用相图.如图10所示,相图被二阶Mott 相变线划分为两个区域,即低温和弱相互作用区的金属相、高温和强相互作用区域的Mott 绝缘体相.随着温度的降低,体系金属-绝缘相变所对应的相互作用也减小.

图10 各向异性ruby 晶格中费米子体系的金属-绝缘相图Fig.10.Metal-Insulator phase diagram of fermions in anisotropic ruby lattice.
4 结论
本文中用半满的哈伯德模型描述各向异性ruby 晶格中费米子.结合团簇动力学平均场理论和连续时间量子蒙特卡罗方法求解杂质模型.在自洽计算的基础上,通过进一步系统的运算后给出体系的单粒子态密度和双占据数.结合态密度和双占据数的演变趋势,最终得到了各向异性ruby 晶格中费米子体系的温度-相互作用相图.研究结果发现了体系低温弱相互作用区的金属相和高温强相互作用区的Mott 绝缘相.
