A Fractal-Fractional Model for the MHD Flow of Casson Fluid in a Channel

Nadeem Ahmad Sheikh,Dennis Ling Chuan Ching,Thabet Abdeljawad,Ilyas Khan,Muhammad Jamil and Kottakkaran Sooppy Nisar

1Fundamental and Applied Science Department,Universiti Teknologi PETRONAS,Perak,32610,Malaysia

2Department of Mathematics,City University of Science and Information Technology,Peshawar,25000,Pakistan

3Department of Mathematics and General Sciences,Prince Sultan University,11586,Riyadh,Saudi Arabia

4Department of Medical Research,China Medical University,40402,Taichung,Taiwan

5Department of Computer Science and Information Engineering,Asia University,Taichung,Taiwan

6Faculty of Mathematics and Statistics,Ton Duc Thang University,Ho Chi Minh City,72915,Vietnam

7Department of Geosciences,Universiti Teknologi PETRONAS,Perak,32610,Malaysia

8Department of Earth Sciences,COMSATS University Islamabad,Abbottabad Campus,Abbottabad,22010,Pakistan

9Department of Mathematics,College of Arts and Sciences,Prince Sattam bin Abdulaziz University,Wadi Aldawaser,11991,Saudi Arabia

Abstract:An emerging definition of the fractal-fractional operator has been used in this study for the modeling of Casson fluid flow.The magnetohydrodynamics flow of Casson fluid has cogent in a channel where the motion of the upper plate generates the flow while the lower plate is at a static position.The proposed model is non-dimensionalized using the Pi-Buckingham theorem to reduce the complexity in solving the model and computation time.The non-dimensional fractal-fractional model with the power-law kernel has been solved through the Laplace transform technique.The Mathcad software has been used for illustration of the influence of various parameters,i.e.,Hartman number,fractal,fractional,and Casson fluid parameters on the velocity of fluid flow.Through graphs and tables,the results have been implemented and it is shown that the boundary conditions are fully satisfied.The results reveal that the flow velocity is decreasing with the increasing values of the Hartman number and is increasing with the increasing values of the Casson fluid parameter.The findings of the fractal-fractional model have elucidated that the memory effect of the flow model has higher quality than the simple fractional and classical models.Furthermore,to show the validity of the obtained closed-form solutions,special cases have been obtained which are in agreement with the already published solutions.

Keywords:Fractal-fractional derivative;Casson fluid;MHD flow;exact solutions

Nomenclature

μ dynamic viscosity

ρthe fluid density

eijthe（i，j）thcomponent of deformation rate

pythe yield stress of the non-Newtonian fluid

π=eijeijthe product of the component of deformation rate itself

πcthe critical value of this product based on the non-Newtonian model μγthe plastic dynamic viscosity

βthe material parameter of Casson fluid

uthe fluid velocity in the x-direction

1 Introduction

The applications of non-Newtonian fluids are quite remarkable and play an important role in the flow modeling in industry and engineering sectors [1-4].The magnetohydrodynamic (MHD) flows of these fluids are widely used in the field of MHD generators,magnetic drug targeting (MDT),MRI,and controlled flows,etc.with increased interest by many researchers [3,5,6].Non-Newtonian fluids exhibit a complex structure that essentially requires some robust mathematical modeling for explanation and depiction.The non-Newtonian fluids flow behaves inversely with the influence of porosity and magnetohydrodynamics [2].To solve the model for the MHD flow of micropolar fluid,the Laplace transformation was applied by Ali et al.[7].MHD flow has been studied for the oscillating plates which include the effects of porous media under heat transfer and radiation [2,5].The convective flow of non-Newtonian fluid over an oscillating plate in porous media was studied by Krishna et al.[8].They have shown the relationship between the pressure gradient and flow velocity.This pressure gradient study has also discussed the relationship with the magnetohydrodynamics and the effects of different materials on the velocity using the Lattice Boltzmann method.The unsteady flow of Casson fluid for the oscillating plate to show the velocity relation in the porous media was studied by Khan et al.[9],who also discussed the velocity and shear stress by obtaining closed-form solutions.Ullah et al.[10]studied the flow of Casson fluid with slip on the stretching sheet.

Fractional derivatives are quite applicable for efficiently discussing the complex real-world problem for the flow of various types of fluids [11].Several numerical simulations have studied water pollution with different applications through Caputo Fabrizio (CF) fractional derivatives [12].These CF fractional derivatives have also been used in heat transfer analysis to get closed-form solutions for unsteady fluid flow over an oscillating plate where the fractional parameter is directly proportional to temperature.At the same time,it is inversely related to the velocity of the fluid.Fractional fluids have higher velocity values,which positively influence fluid flow [13].These tenuous effects of the fluid flow could be efficiently resolved with the help of fractional derivatives [11].The CF fractional derivatives and Atangana-Baleanu (AB) are very useful to identify and calculate the velocity values [14].Fractional partial differential equations had also solved for closed-form solutions by using finite Hankel and Laplace transformation techniques.The numerical analysis of the fractional derivatives highlights a more significant effect on the velocity as compared to ordinary derivatives [15].The fractional model could also apply to Casson fluid along with the energy equations.The Caputo fractional model and the Laplace transformation have also been used to get the solutions with Wright function by Ali et al.[16].AB fractional derivatives and CF fractional derivatives could be used for the demonstration of the heat and mass transfer analysis of free convection flow of Casson fluid.For these types of flows,solutions and results were obtained through the Laplace transformation technique by Sheikh et al.[17].Free convection generalized (Caputo-Fabrizio time-fractional derivatives) flow of Jeffrey fluid was analyzed via the Laplace transformation technique by Saqib et al.[18].They had obtained the exact solutions for velocity and temperature.The results emphasize that fractional flows are relatively swifter than classical flows.Saqib et al.[11]discussed the Atangana-Baleanu (AB) derivatives model for Casson fluid in a microchannel.They have concluded that the fractional parameter considerably influences the viscosity and buoyancy forces.The numerical analysis of nanofluids through a porous media in a vertical channel by applying AB fractional derivative for convection free flow was discussed by Saqib et al.[19].The flow of Casson fluid was considered by Sheikh et al.[20].They studied the Caputo fractional derivative and the flow had modeled using the generalized Fourier and Fick laws.

Carpinteri et al.[21]discussed the fractal-fractional calculus in continuum mechanics.The fractalfractional model for the convective flow in the rotating cavity was considered by Abro et al.[22].They used the Caputo fractional derivative,CF derivatives,and AB derivatives for their analysis.Fractalfractional derivatives for Couette flow by Laplace transformation were applied for viscous fluid flow between two plates considering a constant value of velocity [23].In many real-life phenomena,mathematical modeling with and without fractional calculus is quite applicable especially in engineering and sciences,for instance,[24-35]mathematical biology and infectious diseases [36],market economics[37],and biomedical research [38,39].

Keeping in mind the above literature survey,in this paper we have considered electrically conducted flow of Casson fluid in a channel.The fractal-fractional model has been created for the subject flow using the concept of fractional calculus.The exact solutions have been obtained using the Laplace transform technique.

2 Mathematical Modelling

We have considered the motion of Casson fluid in a vertical channel.The flow is assumed in the direction of the x-axis while the y-axis is taken perpendicular to the plates.The fluid and the plates are at rest when t≤0.At t=0+,the plate at y=d begins to move in its plane with velocity U as shown in Fig.1.

Figure 1:Geometry of the flow

We suppose that the rheological equation for an incompressible Casson fluid is[15,40]:

The flow of Casson fluid is governed by the following partial differential equations[41,42]:

where the initial and boundary conditions are:

Introducing the following dimensionless variables[23]

with initial and boundary conditions in the dimensionless form:

2.1 Fractal-Fractional Model

The fractal-fractional model for the mentioned flow problem,in the generalized form is:

If we assume that v（κ）is continuous in open interval,if v（κ）is fractal differentiable on(a,b)with order δ,then the fractal fractional derivative of v（κ）with order α in Riemann-Liouville sense with power law is presented as [43]

where

2.2 Velocity Profile

Applying the Laplace transform to Eq.(5) using Eq.(6) we arrived at

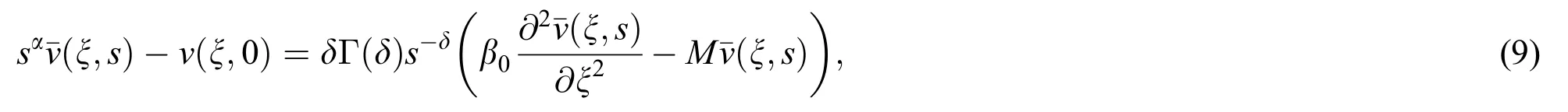
in a suitable form Eq.(9)can be written as

solving Eq.(10),using Eq.(5)we have the following solution:

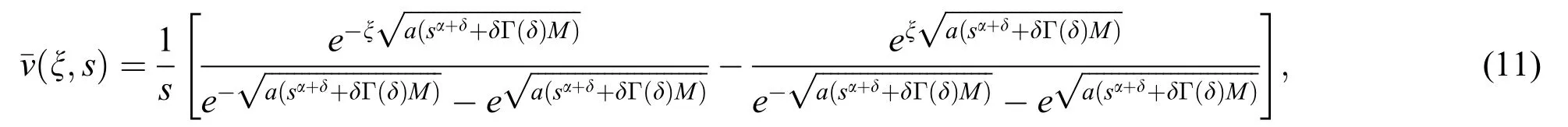
In more suitable form Eq.(11) can be written as:

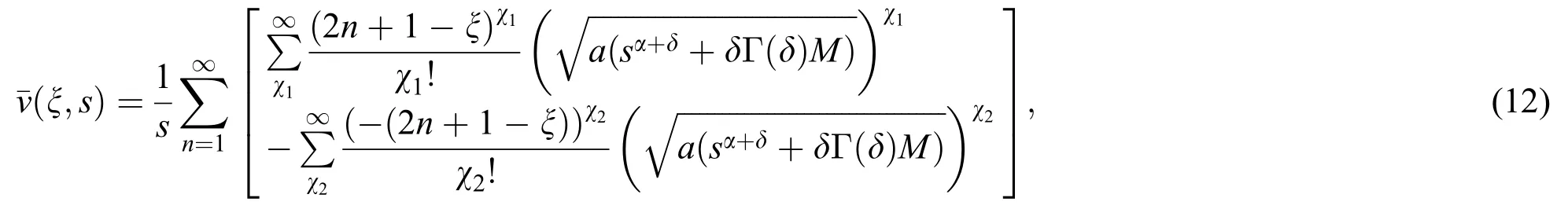
inverting the Laplace transformation of Eq.(12) [23]we have:

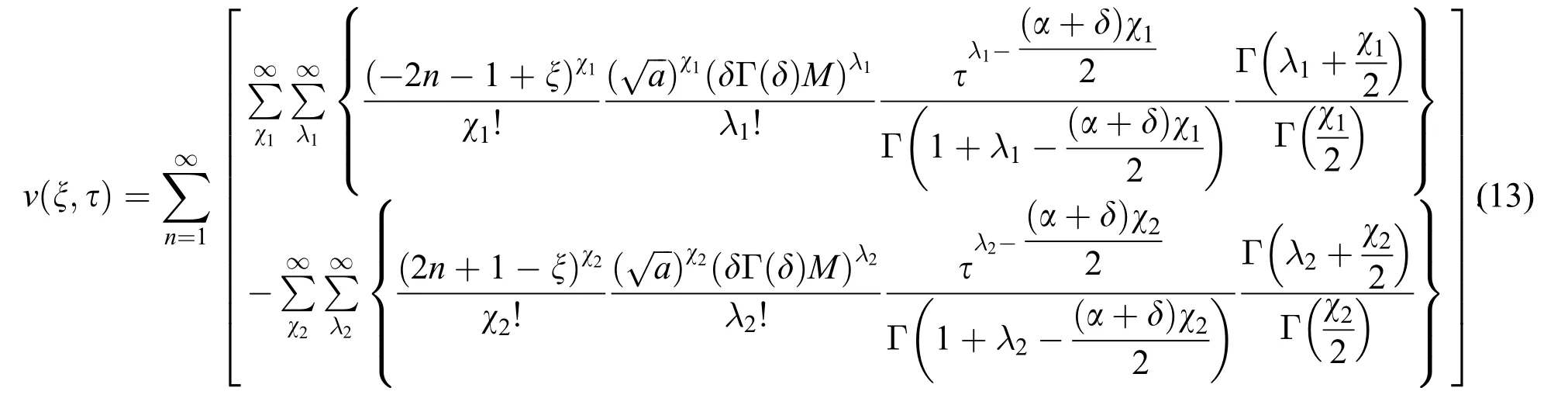
2.3 Limiting Cases

Validating results,the present solutions have reduced to the already published results in the literature,and the solutions for some other well-known flows have been obtained.

2.3.1 Case 1(Newtonian Fluid)

For β→∞the obtained solution is reduced to the following form:

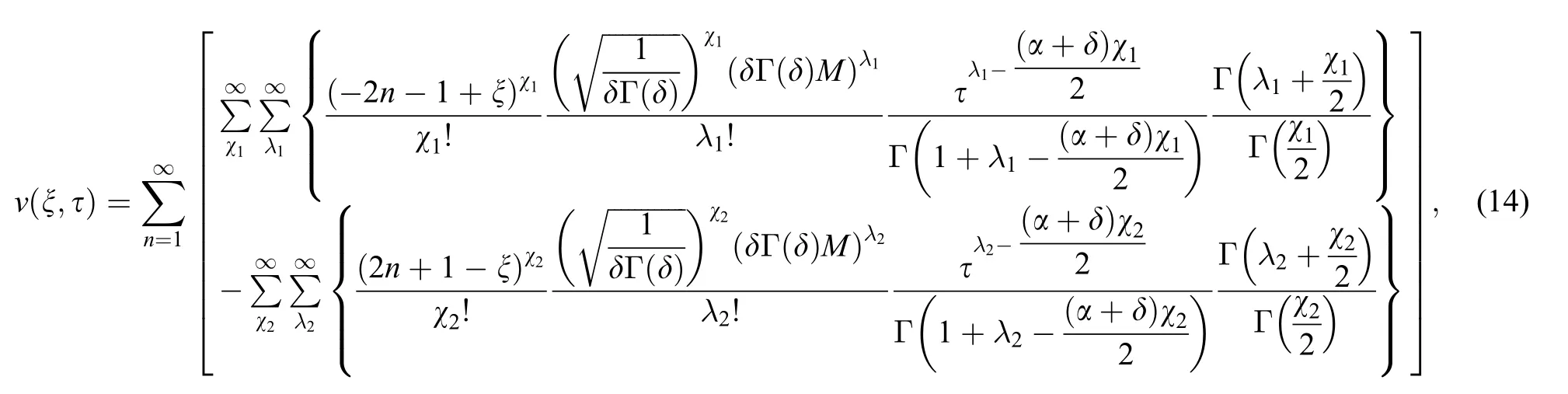
which is identical to the solution calculated by[23].

2.3.2 Case 2(Solution for fractional model)

For δ=1 the obtained solution is reduced to the corresponding fractional model:

2.3.3 Case 3(Solution of integer order model)

For α=δ=1 the obtained solution is reduced to the corresponding classical model:

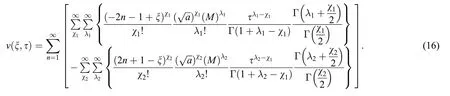
3 Results and Discussion

In the present study,we have considered the fractal-fractional model of the MHD flow of Casson fluid in a channel.The flow has been induced due to the constant velocity of the upper plate.To better understand the flow behavior,graphs have been plotted for velocity profile,and the results shown in tables.

The influence of the Hartman number is shown in Fig.2.The velocity of the Casson fluid is decreasing with the increasing values of the Hartman number.Lorentz’s forces,which are opposing forces to the flow,are more potent for the rising values of the Hartman number.This behavior is also shown in Tab.1,which clearly shows that the obtained solutions are satisfying the imposed boundary conditions.

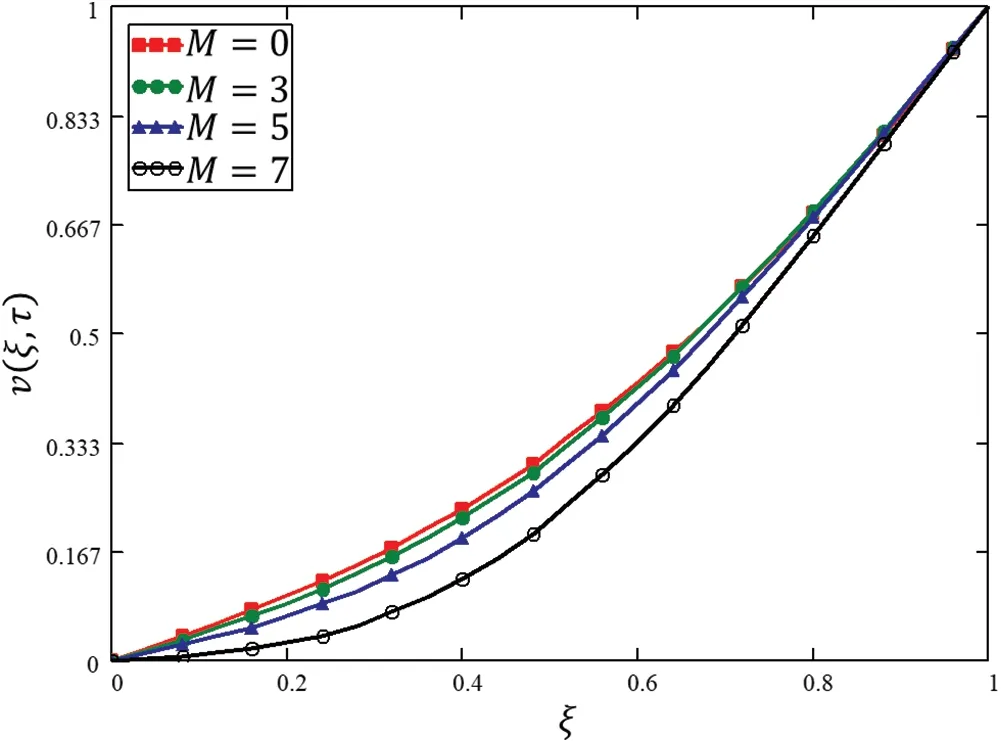
Figure 2:Variations in velocity profile against ξ for different values of M

Table 1:Variations in velocity profile against ξ for different values of M

The effect of the fractional parameter is shown in Fig.3 and presented in Tab.2.Variations in velocity are shown for different values of α,and despite the increasing or decreasing behavior of the velocity,this figure shows that we can draw many graphs for the velocity while keeping the physical parameters constant.This effect is known as a memory effect,which can be described by α.

The graph is plotted for δ in Fig.4 and presented in Tab.3.Despite the increasing or decreasing behavior of the velocity,this figure shows that we can draw many graphs for the velocity while keeping the physical parameters constant.The important fact is that both the fractional and fractal parameters are describing the memory,and together these can describe the memory better than the fractional and classical models.

To show the effect of the Casson fluid parameter β,Fig.5 has been plotted.It has been depicted from this figure that velocity increases with the increasing values of β.Physically,the increasing values of β reduces the thickness of the boundary layer.We can say that for a huge value of β the fluid will behave like a Newtonian fluid.

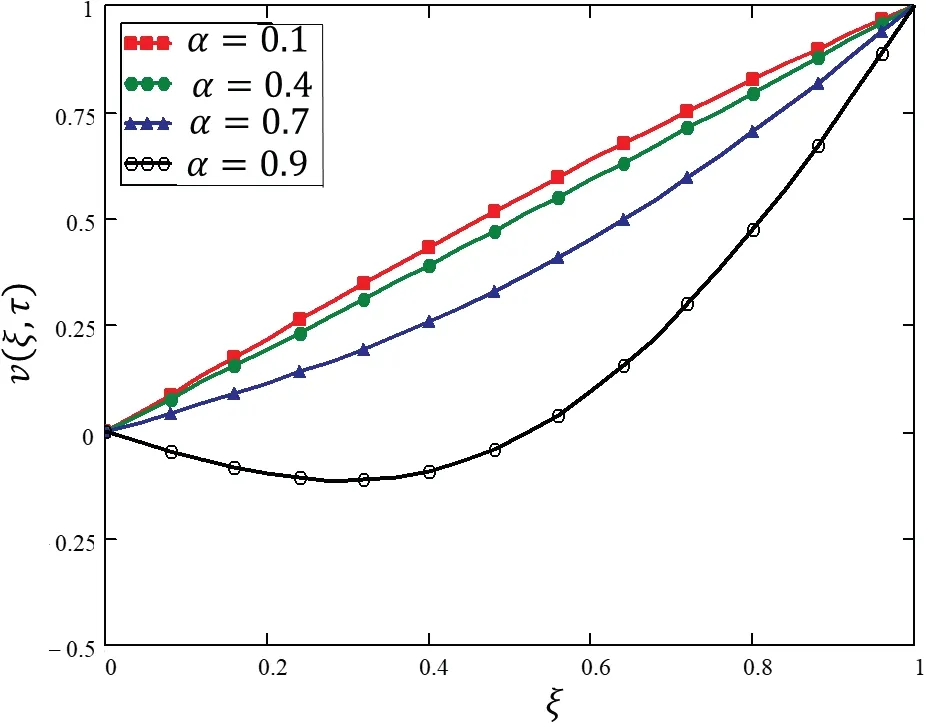
Figure 3:Variations in velocity profile against ξ for different values of α

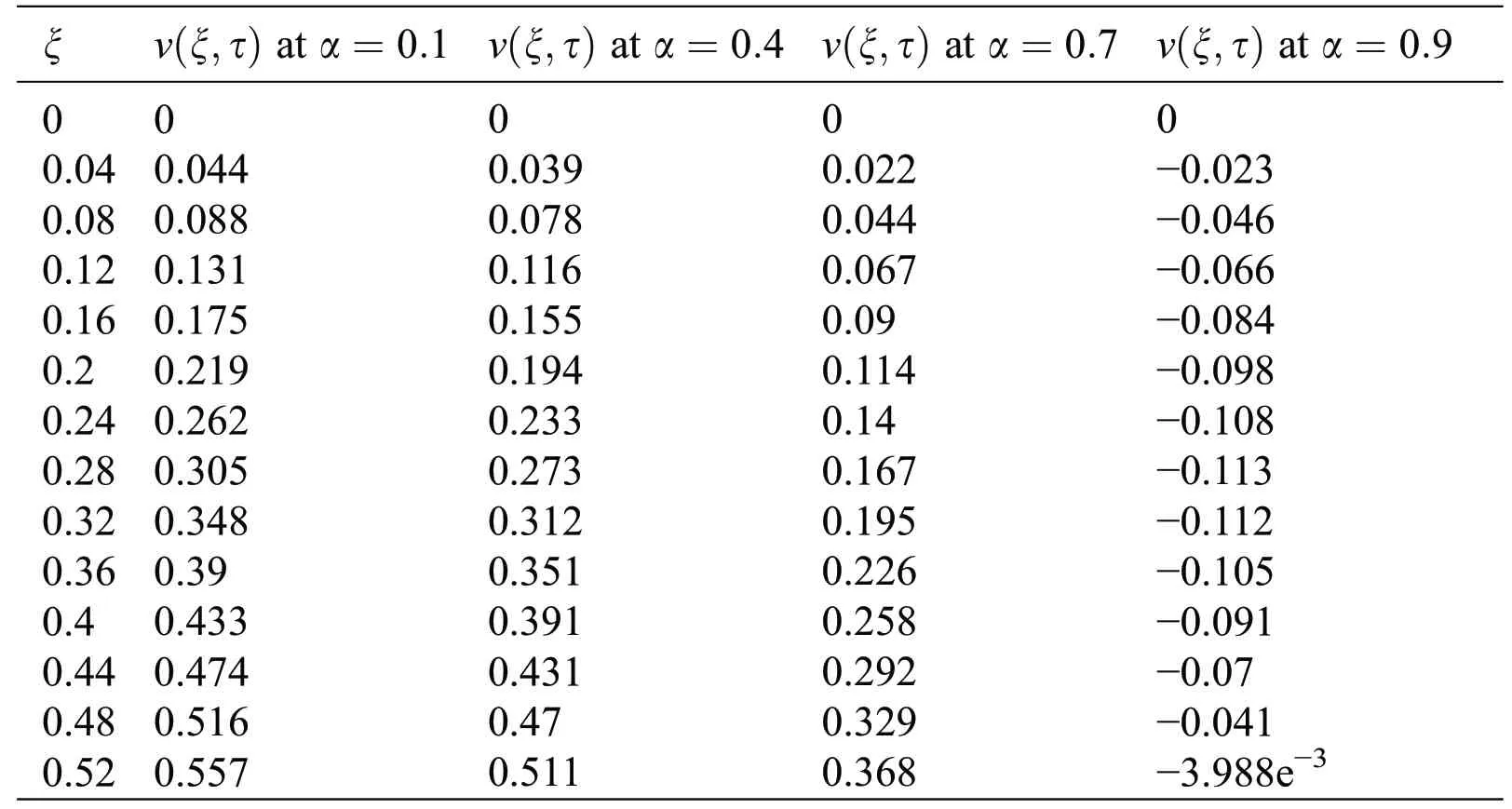
Table 2:Variations in velocity profile against ξ for different values of α

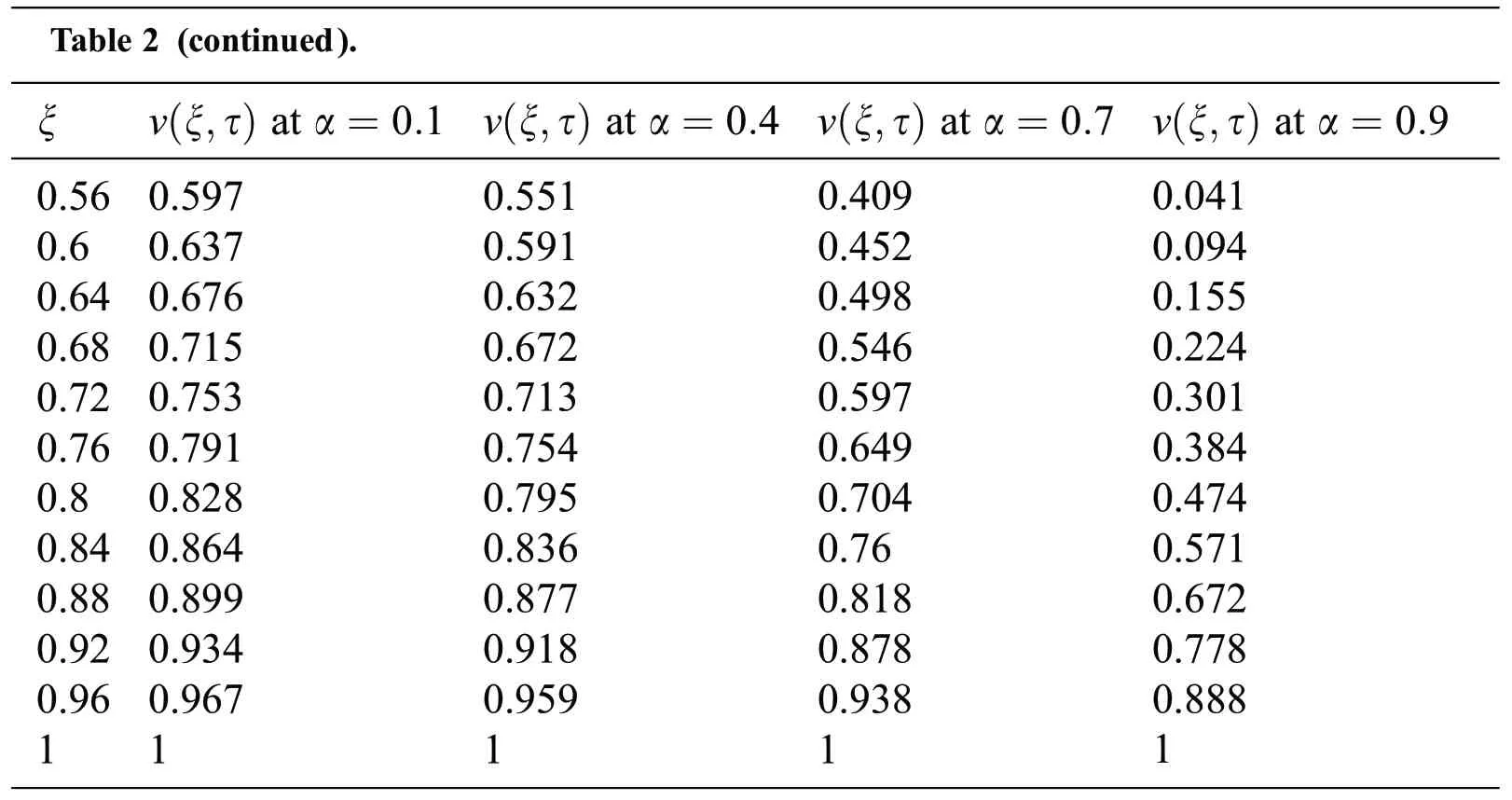
Table 2 (continued).ξ v（ξ，τ） at α=0.1 v（ξ，τ） at α=0.4 v（ξ，τ）at α=0.7 v（ξ，τ）at α=0.9 0.56 0.6 0.64 0.68 0.72 0.76 0.8 0.84 0.88 0.92 0.96 1 0.597 0.637 0.676 0.715 0.753 0.791 0.828 0.864 0.899 0.934 0.967 1 0.551 0.591 0.632 0.672 0.713 0.754 0.795 0.836 0.877 0.918 0.959 1 0.409 0.452 0.498 0.546 0.597 0.649 0.704 0.76 0.818 0.878 0.938 1 0.041 0.094 0.155 0.224 0.301 0.384 0.474 0.571 0.672 0.778 0.888 1

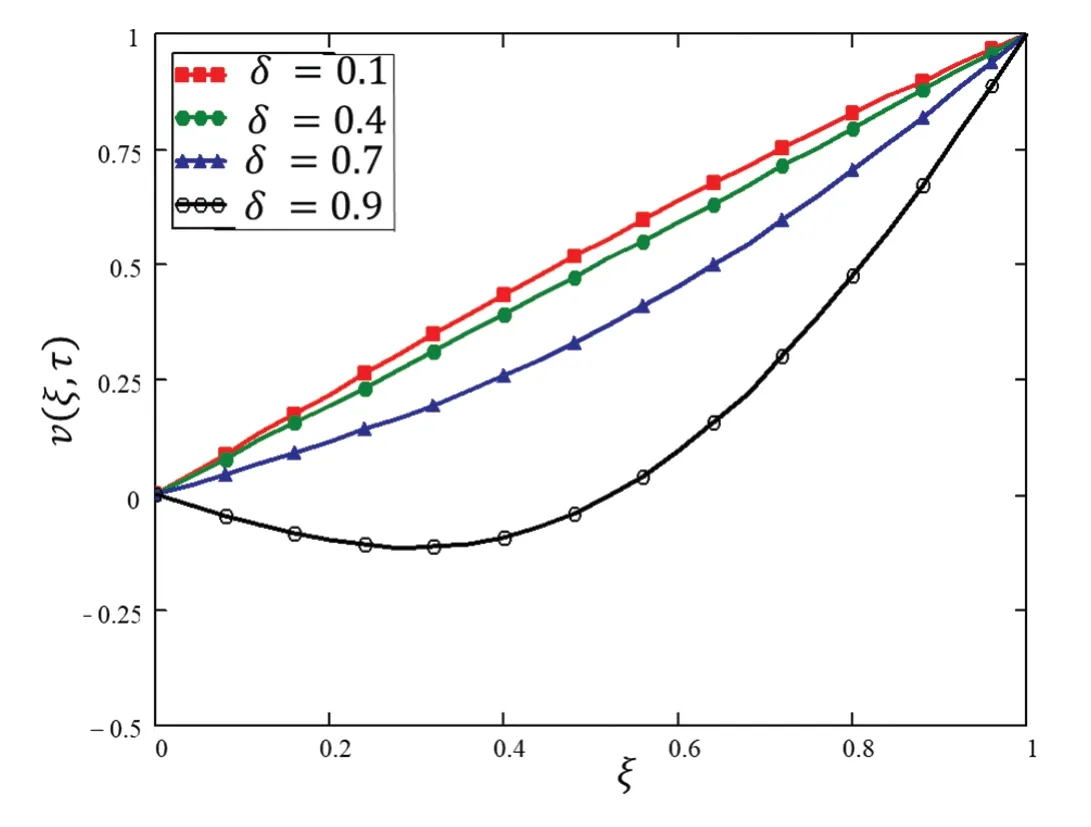
Figure 4:Variations in velocity profile against ξ for different values of δ

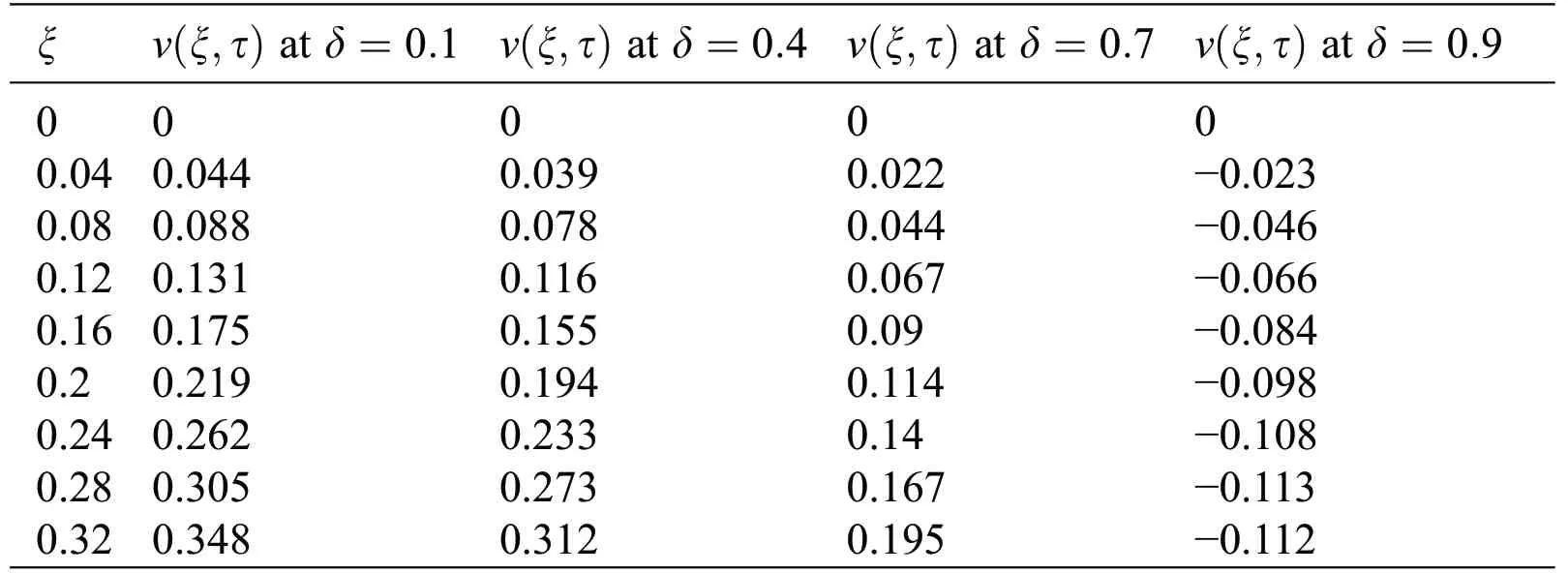
Table 3:Variations in velocity profile against ξ for different values of δ

(Continued)

Table 3 (continued).ξ v（ξ，τ） at δ=0.1 v（ξ，τ） at δ=0.4 v（ξ，τ）at δ=0.7 v（ξ，τ）at δ=0.9 0.36 0.4 0.44 0.48 0.52 0.56 0.6 0.64 0.68 0.72 0.76 0.8 0.84 0.88 0.92 0.96 1 0.39 0.433 0.474 0.516 0.557 0.597 0.637 0.676 0.715 0.753 0.791 0.828 0.864 0.899 0.934 0.967 1 0.351 0.391 0.431 0.47 0.511 0.551 0.591 0.632 0.672 0.713 0.754 0.795 0.836 0.877 0.918 0.959 1 0.226 0.258 0.292 0.329 0.368 0.409 0.452 0.498 0.546 0.597 0.649 0.704 0.76 0.818 0.878 0.938 1−0.105−0.091−0.07−0.041−3.988e−3 0.041 0.094 0.155 0.224 0.301 0.384 0.474 0.571 0.672 0.778 0.888 1

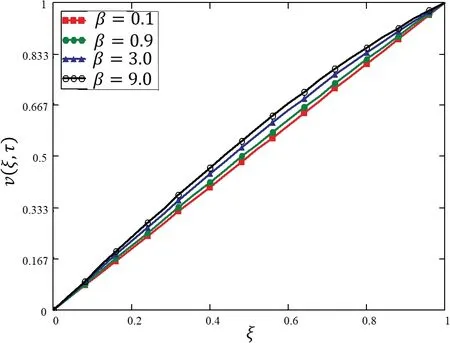
Figure 5:Variations in velocity profile against ξ for different values of β

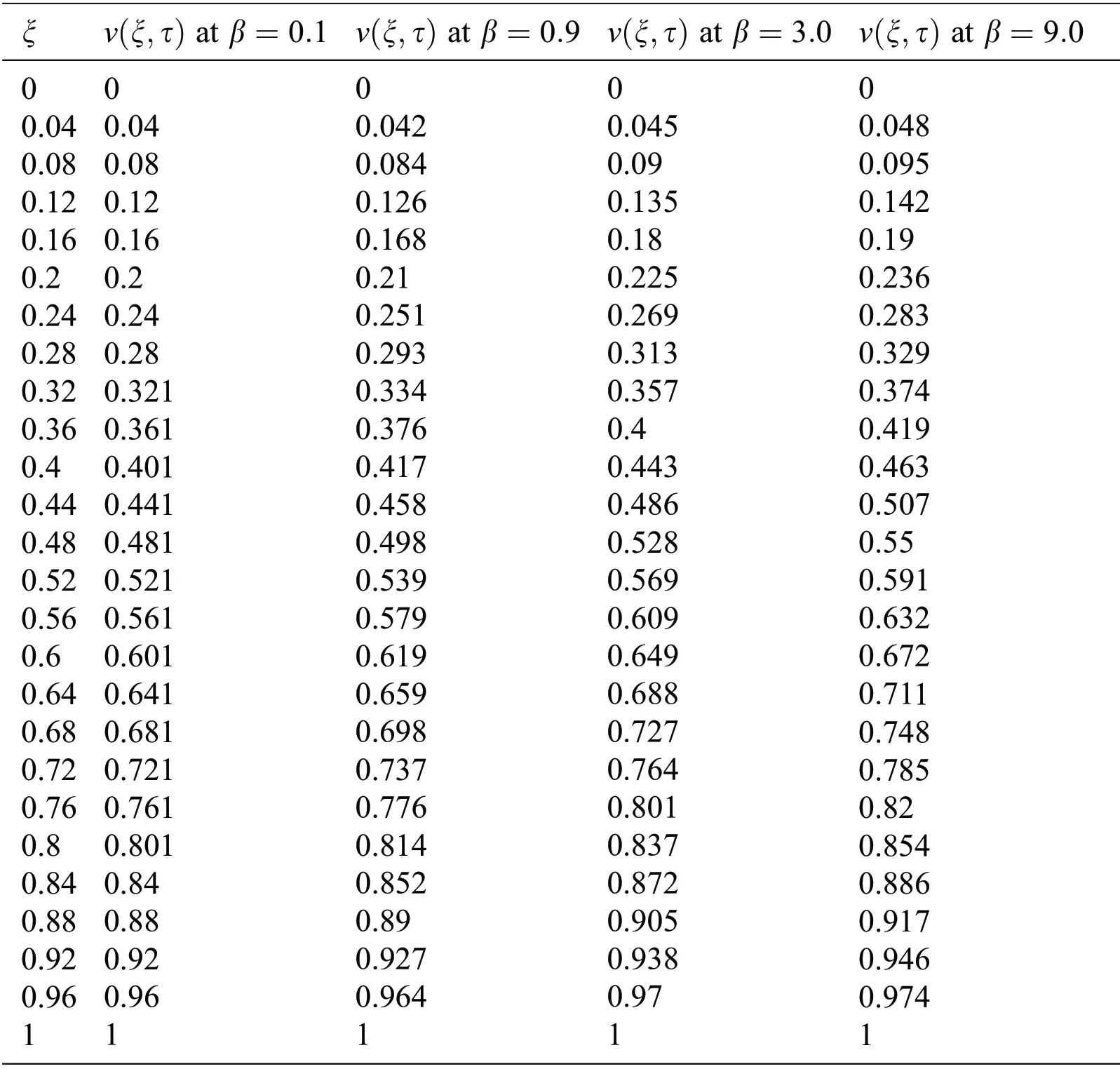
Table 4:Variations in velocity profile against ξ for different values of β

4 Conclusion

In this study,a new approach has been used to develop the fractal-fractional model of the Casson fluid.The Laplace transformation technique has been used to solve the model for the exact solutions.The obtained solutions are plotted and presented in tables.The main outcomes of the present study are:

1.The Laplace transform is a better tool to handle the fractal-fractional models.

2.The Casson fluid velocity is higher for the greater values of β,which shows that the fluid will behave like a Newtonian viscous fluid.

3.The variations for different values of α and δ in velocity have been plotted.It is important here to mention that we have separate lines for one value of time.This effect shows the memory effect in the fluid,which cannot be demonstrated from the integer-order model.

Funding Statement:This work was funded by Yayasan Universiti Teknologi PETRONAS(Y.U.T.P.),Cost Center 015LC0-278.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.