新型太阳能干燥系统空气侧流动及传热性能数值模拟分析*

关志中 罗会龙 张国健 史宏岗 李云涛 刘禹琳

(昆明理工大学建筑工程学院 昆明 650500)

0 引言

太阳能干燥系统具有节能环保等优点。目前，以空气为换热介质的干燥系统由于空气的密度小、比热小、导热系数低，使得太阳能空气集热器的热效率较低。以水为介质的太阳能干燥系统，现阶段通常把太阳能集热器获得的热量以热水的形式储存于保温水箱里面，通过循环泵使保温水箱中温度较高的水与空气进行热交换，加热空气用于热风干燥。在循环泵的作用下，保温水箱中的水被搅合，其温度分布较均匀，上下部温度均较高。降低了太阳能集热器的集热效率和太阳能干燥系统的热利用率。因此，探究提升太阳能干燥系统的集热效率和热利用率对太阳能干燥的发展具有重要意义。

国内外研究人员通过研究加装辅助加热设备和改变干燥系统构成来提升太阳能干燥系统的效率。孟翔宇等[1]提出了结合金属氢化物热泵的特点,一种耦合氢能的太阳能热泵干燥系统，该系统与普通热泵干燥系统相比提高了61% ,比热泵-微波联合干燥系统提高了147%,比 CO2热泵干燥系统提高了25%。许彩霞等[2]用热泵-太阳能联合系统干燥木材，得出热泵-太阳能联合系统相比常规能源方法节能70%。史海舰等[3]提出智能化控制新型太阳能-辅助加热的干燥系统，有利于提升农牧产品干燥的效率和节约能耗。MOHANRAJ M[4]研究了以R22 为制冷剂的直膨式太阳热泵干燥系统的性能,与空气源热泵干燥系统相比效果更优。但添加辅助加热设备，存在设备初投资高、系统自动化运行要求高、维护要求高等问题。目前，关于太阳能干燥系统改进研究的文献很少。

综上所述，本文利用热管优良的导热性能及等温传热的特点，对系统结构进行优化，提出了新型太阳能干燥系统，并对其空气侧进行数值模拟，为热管在其中的应用提供依据。

1 系统构成形式和工作流程

该太阳能干燥系统如图1所示，分别由Ⅰ太阳能集热子系统、Ⅱ热风干燥子系统、水蓄热-空气加热装置和温湿度计等主要部件组成。其工作流程如下：太阳能集热器出水口通过上循环管与保温水箱上循环口连接，太阳能集热器进水口通过下循环管与保温水箱下循环口连接。太阳能集热器吸收太阳辐射，加热集热器中的水，加热后的水密度变轻，在热虹吸压头的作用下通过上循环管进入热分层保温水箱的上部。保温水箱上部温度较高的热水直接加热热管的蒸发段，蒸发段内的液体工质受热蒸发，变成气体上升至热管的上端即冷凝段，与空气加热腔中的空气进行冷凝换热，释放冷凝热以加热空气加热腔中的空气，用于热风干燥。与此同时，气态工质释放冷凝热变成液体，依靠重力流回热管蒸发段再次蒸发。如此循环往复，热管从热分层保温水箱上部吸热，用于加热空气加热腔中的空气。加热后的空气通过送风风机经保温送风管送入干燥室，用于热风干燥。回风风机将干燥室排风口一部分热湿气流排到室外，另一部分通过保温回风管送入空气加热腔再次加热。

Ⅰ—太阳能集热子系统；Ⅱ—热风干燥子系统；1—太阳能集热器；2—太阳能集热器出水口；3—热管；4—水箱；5—太阳能集热器出水口；6—排污口；7—补水箱；8—隔板；9—空气加热腔出风口；10—空气加热腔；11—送风风机；12—干燥室；13—第一温湿度计；14—回风风机；15—排风调节阀；16—回风调节阀；17—空气加热腔出风口；18—第二温湿度计；19—新风调节阀。

2 数值模拟

2.1 数学及物理模型

由于传热过程复杂，为降低求解难度，对模型进行简化：①在传热和流动过程中都处于稳态；②在传热过程中不考虑辐射换热； ③流体不可压缩、物理性质稳定,空气与换热壁面无滑移。根据模型假设，在空气加热腔里空气的流动采用k-ε模型。

水蓄热-空气加热装置结构如图2所示。在水蓄热-空气加热装置的中部设置隔板，将其分隔成上、下两个腔，上部为空气加热腔，下部为保温水箱。隔板上开有若干个小孔，热管通过小孔由密封圈固定在隔板上。热管下端为蒸发端从热分层保温水箱吸热，热管上端为冷凝段向空气加热腔放热，以加热空气用于热风干燥。

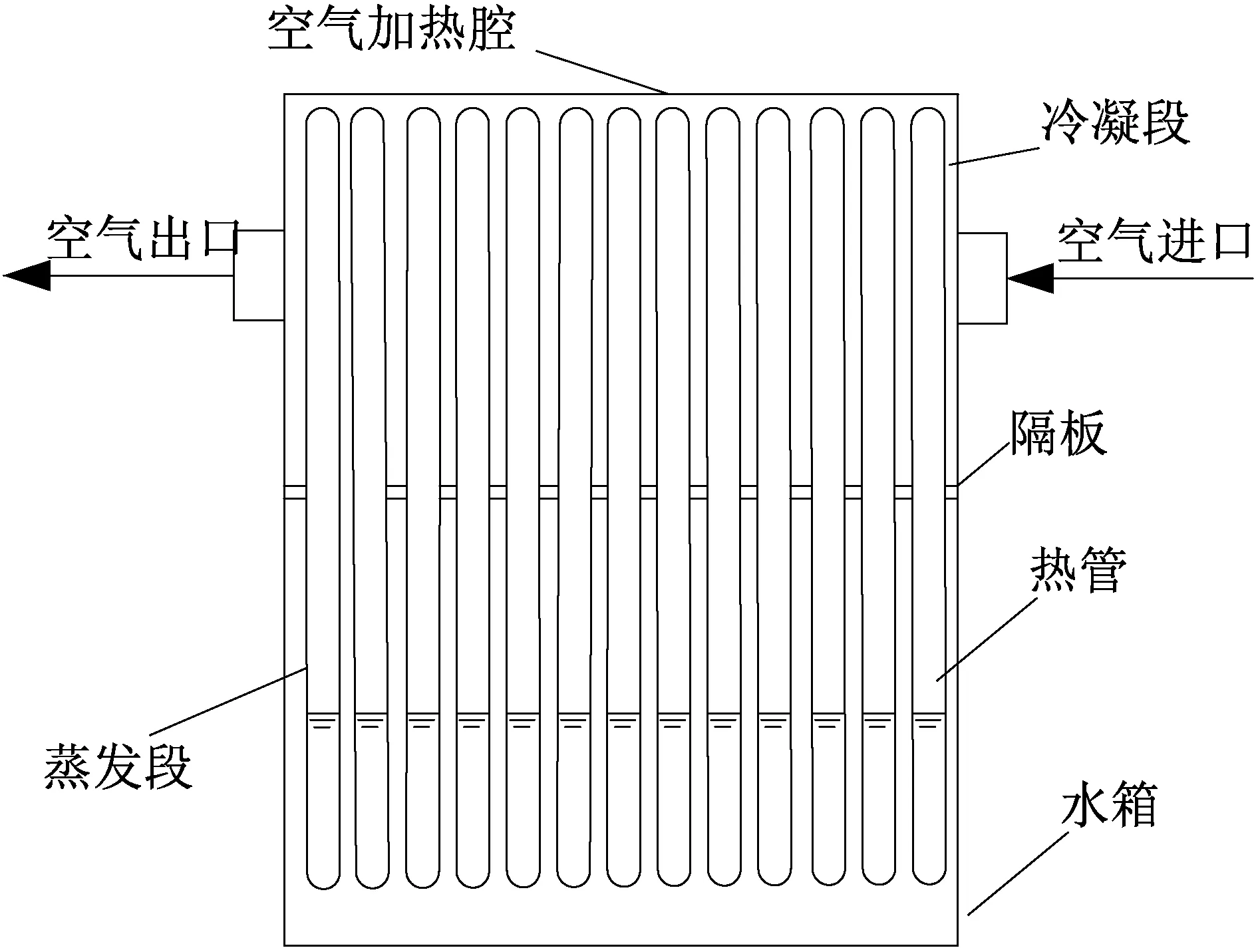
图2 水蓄热-空气加热装置结构示意

本文根据文献[5]，在保证热管数量和几何参数相同的情况下，设计了3种不同的热管排列方式进行模拟。热管的排布方式主要有正方形、正三角形和转三角形，如图3所示。

(a)正方形 (b)正三角形 (c)转三角形

2.2 网格划分

网格划分直接影响模拟计算结果，其网格质量对模拟计算的精度有较大的影响。网格主要分为结构化网格与非结构化网格。结构化网格具有很多优点，比如网格生成速度快、网格生成质量好和数据结构简单等；非结构化网格主要是弥补结构化网格不能解决任意形状和任意连通区域的网格剖分的不足[6]。本文采用混合网格划分方法，网格划分后进行网格质量检测，对正交质量和扭曲度进行评估，检查后所有的网格满足要求。

为更好进行空气加热腔内的传热模拟计算，对空气流体区域与热管接触面进行细致的网格划分。同时在初始条件和边界相同的情况下，对模型进行网格无关性分析如图4所示。由图4可知，随着网格数增加，出口温度也随之上升，当网格数大于1.5×105时，出口温度不随网格数增加而发生明显变化。因此，综合考虑计算成本和精度，最终采用网格数为 170 039进行FLUENT仿真模拟。

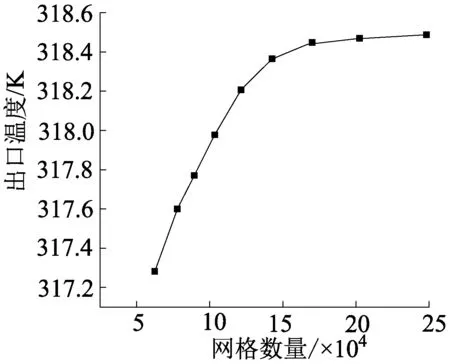
图4 网格无关性分析

2.3 初始条件及求解设置

(1)进风口设置为速度入口边界条件，出风口设置为压力出口边界条件。

(2)空气加热腔与外界相交的面设置为绝热壁面。

(3)由于要考虑到重力对于流场的影响，重力加速度设置为9.81 m /s2。

(4)本文选用SIMPLEC算法进行求解，选择Green-Gauss Cell Base，在进行分析的时候选择能量方程和Realizablek-ε方程湍流模型;采用稳态迭代计算方法，计算完成后，迭代收敛达到10-3以下。

3 计算结果及分析

3.1 排列方式的影响

从热管排列方式在出口处的温度分布云图(图5)可以看出，在相同风速和相同热源加热情况下，3种排列方式的出口温度梯度分布较为明显。

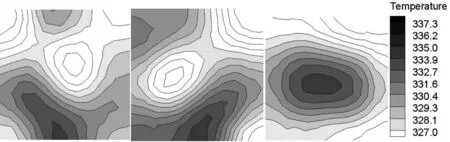
(a)正方形 (b)正三角形 (c)转三角形

热管呈正方形排列时，最高温度在中下部为334.3 K。热管呈正三角型分布时,最高温度分布中心为337.5 K。热管为转三角形分布时，最高温度在右下角为343.7 K。由图6可以看出3种排布方式加热空气能力随着离入口距离的增加温度逐渐升高。在温度增量相同时，正三角形和转三角形排布方式的热管加热空气能力明显高于正方形排布方式，正三角形排布的加热能力大于转三角形。正三角形排布的换热量对于正方形排布和转三角形排布换热量增加了约26 W和39 W，提高了约3.2%和4.9%。在管间距相同情况下，正三角形排列使空气与热管间扰动增强,换热效果好。

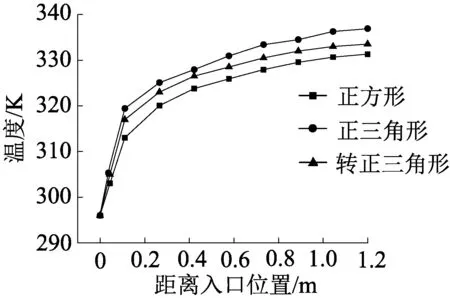
图6 热管3种排列方式温度变化

3.2 进口速度的影响

由图7可以看出，随着干燥空气不断的深入，空气温度开始逐渐升高，温度升高的范围基本都在热管周围。当进口流速不断减小时，进出口温差变大，传热量也变大。2 m/s时热管周围换热量明显大于其他风速，换热更加充分出口温度更高。由图8、图9可以看出，流速为2 m/s时，换热量最大为1 141 W；流速为5 m/s时，换热量最小为447 W。风速从5 m/s减小到4 m/s，换热量增加18%。风速从4 m/s减小到3 m/s，换热量增加37%。风速从3 m/s减小到2 m/s，换热量增加52%。由此可以看出，随着风速的减小，空气在管道内滞留的时间增加，换热量增大。但在实际干燥过程为了选择合适的风速需要考虑空气的出口温度以及干燥所需的时间。因为风速选择过大，空气无法与热管进行充分换热导致无法满足出口温度达到干燥工艺的要求；风速选择过小，导致干燥速率降低和干燥效果不明显，以至于降低经济性[7]。为了满足出口温度和干燥时间的要求，空气出口速度选择3 m/s较为合适。

(a)2 m/s (b)3 m/s (c)4 m/s (d)5 m/s

图8 不同风速随入口位置的温度变化

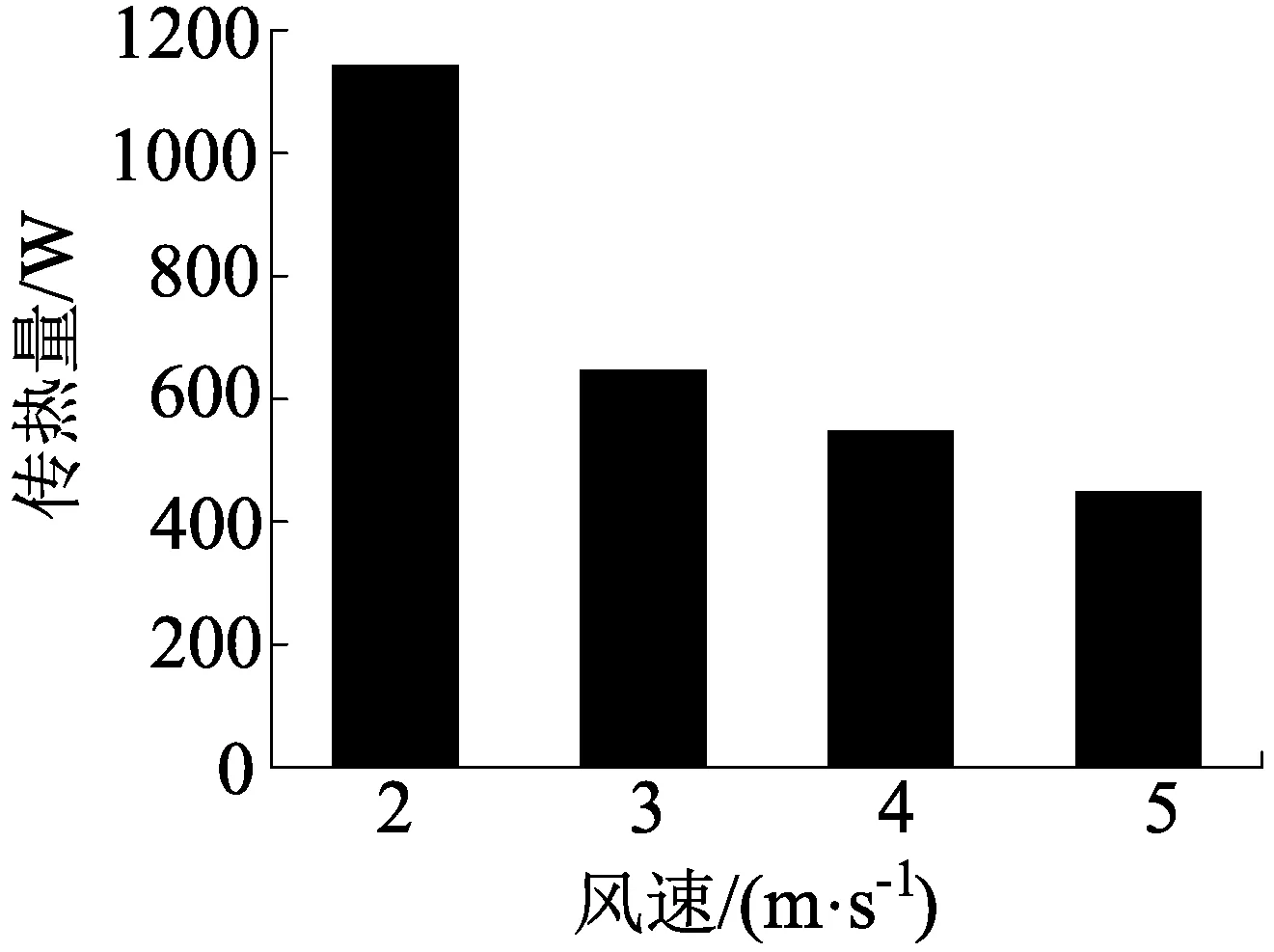
图9 不同风速与换热量的关系

3.3 管径与管距的影响

由图10可以看出，随着管径的增大，空气与热管的接触面积增加，导致换热量增大。同时出口温度的增加呈线性分布。当管距减小时，空气的过流面积减小，热管之间的流体流速加大，扰动增强。因此热管的对流换热系数相应增加，热阻减小，使热管的换热能力增强。为了最大限度加热空气进行干燥，取选择热管管径为50 mm、管距为30 mm较为合理。

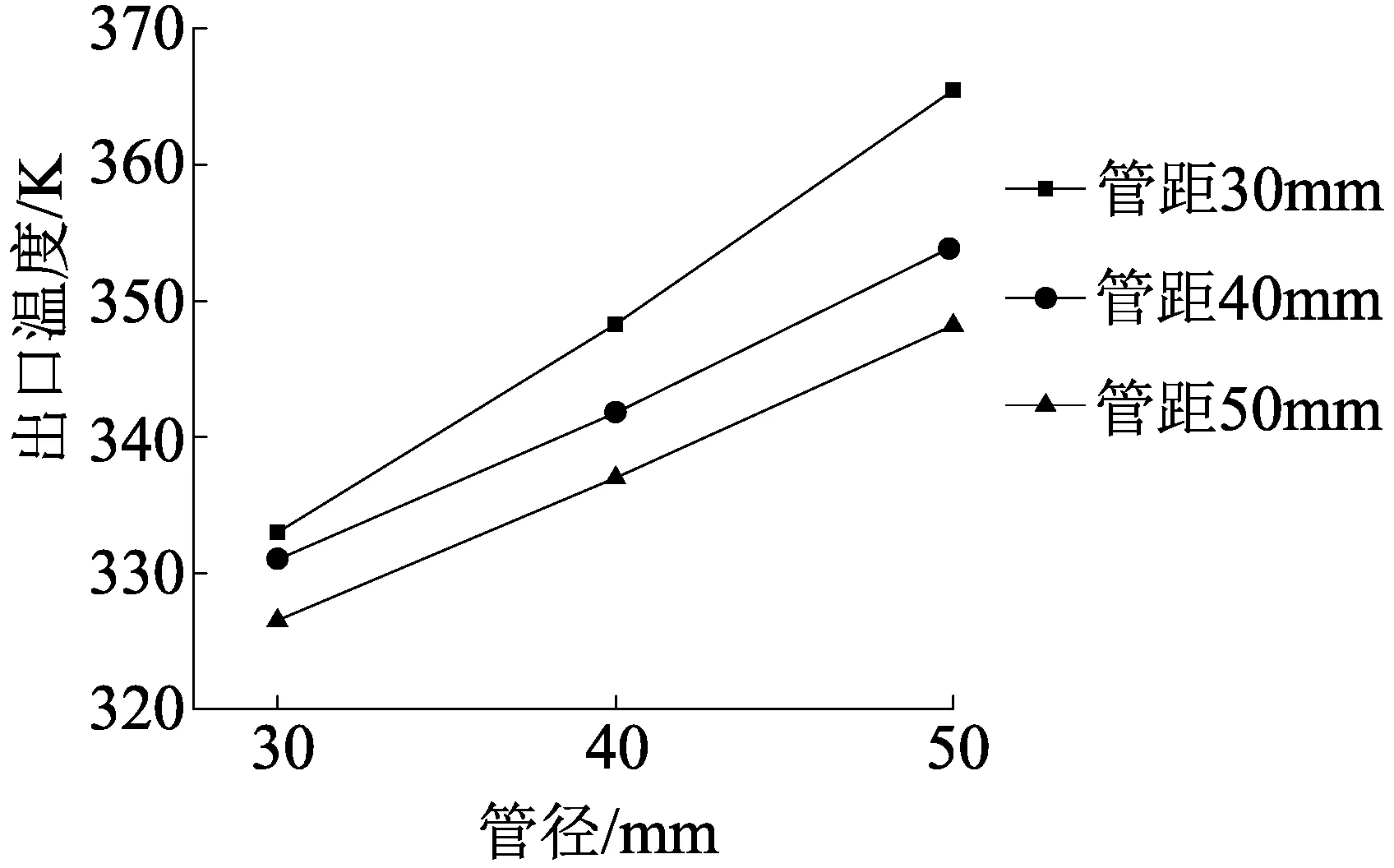
图10 不同管距与管径的出口温度变化

4 结论

(1)正三角形排布的热管换热量特性较正方形排布和转三角形排布提高了3.2%和4.9%，热管排布方式选择正三角形较为合理。

(2)热管与空气的换热量随着空气流速的减小，空气在管道内滞留的时间增加，换热量增大。同时考虑到干燥时间的影响，空气的进口速度选择3 m/s较为合理。

(3)随着管径的增大、管距的减小，空气与热管换热更加充分，选择管径为50 mm、管距30 mm最佳。