基于小波变换的电力系统短路故障定位研究

李佳佳，殷军光，郭龙超，樊晓虹

(河南城建学院 电气与控制工程学院，河南 平顶山 467036)

我国能源集中分布在西部和北部地区，电力消费集中在东部和中部地区，大容量、远距离输电是我国电网的运行现状。为保证用户持续可靠、高质量用电，对输配电网络进行故障定位势在必行。小波变换是一种新的变换分析方法，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的有效工具，广泛应用于图像处理中。文献[1]采用行波在输电线路上的理论计算方法和传输特性,提出了波阻抗和波速的简易测量处理方法。文献[2]提出将小波变换应用于输配电系统的方法，采用基于双端电气量的行波测距，然而未考虑行波波速的不确定性对故障定位的影响。本文采用双端行波测距方法和小波分析配合使用的识别方法进行故障暂态信息行波波头的提取，通过阈值触发确定故障点波头时间，利用零模行波在故障时的行波波速，从而测量故障距离。

1 基于小波分析的故障检测系统

文献[3]已证明采用双端故障检测时，到达测量点的第一个反向行波波头最易于捕捉。文献[4]提出利用Haar和Daubechies小波提取不同故障时暂态直流分量，非故障相直流分量几乎为0，故障相直流分量极大，因此，可将此作为故障选相的依据。达到精确选相和快速准确定位，本文设计的算法步骤如图1所示。

图1 故障检测系统算法

1.1 故障信号提取

故障点的行波向线路两端传播，假设用线路上的位置x和时间t为变量的偏微分方程表示单根的无损分布参数线路上的电压u与电流i[5],则

(1)

其中，L——线路单位长度的电感，C——线路单位长度的电容。

式(1)对x，t进行微分变换后得到波动方程

(2)

式(2)的达朗贝尔(D’Alember)分解为

(3)

当线路发生单相接地故障时，三相线路会产生暂态故障行波。通过对行波进行Clarke相模变换，便于分析计算并消除相间电磁耦合，变换公式为：

(4)

(5)

其中，uα、uβ、uc分别为线路的三相电压行波分量，分别对应α、β、0模分量；iα、iβ、i0分别为电流行波的α、β、0模分量。

方向行波的模量表示为：

(6)

(7)

其中，S1α、S1β、S10分别为正方向行波的α、β、0模分量;S2α、S2β、S20分别为反方向行波的α、β、0模分量；zα、zβ、z0分别为α、β、0模分量行波对应的波阻抗；S1α为正方向的行波波形，对S1α进行小波变换，通过模极大值提取确定故障时间。

1.2 奇异点的定位

信号的突变性检测是先对原信号在不同尺度上进行“磨光”，再用磨光后信号的一阶或二阶导数检测其极值点或过零点。对信号进行磨光处理，主要是为去除噪声而不是边缘，因此磨光函数应是局部化的。常用的磨光函数(又称平滑函数)θ(t)可选取Gauss函数或B样条函数，磨光函数满足[6]

(8)

(9)

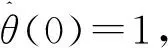
(10)

(11)

2 仿真实例及分析

以某220 kV输电系统为例，利用MATLAB/SIMULINK搭建故障线路仿真模型，如图2所示。

图2 输电网络接地短路故障仿真模型

该工程输电线路全长200 km,在0.01 s开始出现a相接地故障，输电线均采用统一型号的钢芯铝绞线。表1为系统仿真设计参数设置。

表1 系统仿真设计参数设置

当a相发生单相接地短路故障时，故障点的三相电压、电流变化分别如图3、图4所示。

图3 a相接地短路时故障点三相电压信号

图4 a相接地短路时故障点三相电流信号

利用MATLAB/SIMULINK搭建提取故障相直流分量子模块，子模块内部结构如图5所示，子模块如图6(a)所示，通过识别提取到的直流分量跃变时间以此表示故障所在相，如图6(b)所示。

图5 提取衰减直流分量子模块内部模型

模型time模块数据为a相故障发生时间，由于该提取直流分量的方法有一定延时，此时间作为显示该相发生故障，b、c非故障相显示为0。由图6(b)也可判断出，当发生接地故障时，a相电流直流分量跃变为极大值，其他相几乎为零，为防止误判，通常设置阈值TH，TH设定为60。当衰减直流分量的值不大于阈值TH时，判定输电线路为正常运行状态；当某相衰减直流分量的值大于阈值TH时，判定该相发生故障。

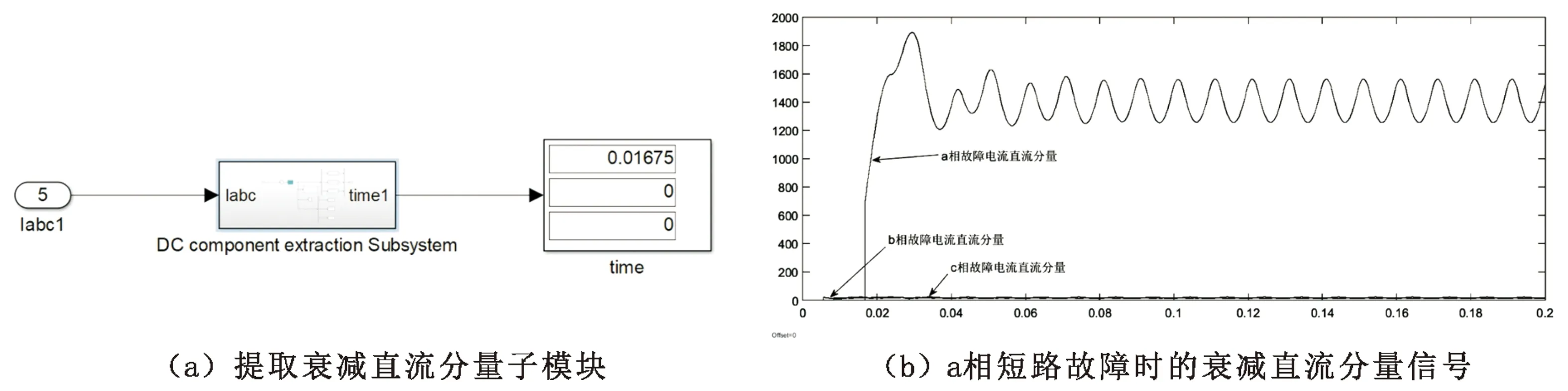
图6 模型实测数据示例

提取到的M端行波如图7所示,N端行波如图8所示。

图7 提取到M端行波信号

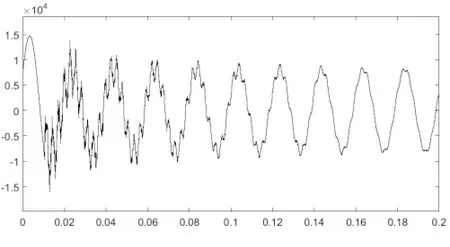
图8 提取到N端行波信号

通过一维小波工具箱进行小波分析，对M端行波通过db5进行5层分解，得到的信号如图9所示，对N端行波通过db5进行5层分解，得到的信号如图10所示，在经过5层小波分解之后，得到的逼近信号和细节信号，均选择第三层细节信号。

图9 M端行波信号进行小波分析

图10 N端行波信号进行小波分析

由图9可知，M端检测到时间为(2 073×5) μs=10 365 μs。由图10可知，N端检测到时间为(2 041×5) μs=10 205 μs。通过计算可得出故障点距离M端的距离为123.195 4 km，误差为0.16%。

利用提取到的小波信号，进行模极大值转换后，利用阈值触发法直接提取波头时间，进而计算出故障距离，此过程可通过MATLAB/SIMULINK内部运算，所以快速、方便易于操作，运用此模型模拟不同故障点的情况，如表2所示。

表2 不同距离情况下的测距结果

由表2可知，对于不同的故障位置，提出的故障测距方法均能实现故障定位，并且定位误差小于2%，满足故障定位的误差要求。同时，提出的故障选相方法能准确地选择出故障相，选相成功率为100 %，阈值TH 的取值应设置在(50,100)区间，以确保阈值大于故障相直流分量一个数量级，提高选相的准确性与灵敏度。仿真表明，提出的故障定位与故障选相方法不受故障位置的影响。

3 结论

依据衰减直流分量的特性，通过比较故障相与非故障相的值，达到故障线路选相的目的。由于线路发生故障后最先到达检测点的反行波头易于捕获的特点，采用反行波进行故障定位,同时采用易于检测信号奇异性的Mallat算法求取反行波信号的模极大值点，进一步提高波头捕捉的可靠性。根据线路中导线的不同类型，采用不同的波速进行故障定位计算。通过MATLAB/SIMULINK将各个步骤进行模块化，依据软件强大的运算能力，进行数值运算，最终可方便判断出故障相，直观得出故障距离。仿真结果表明，本文模型可行性高，可快速准确定位故障相并显示距离。