Temporal Stability Analysis of Magnetized Hybrid Nanofluid Propagating through an Unsteady Shrinking Sheet:Partial Slip Conditions

Liaquat Ali Lund,Zurni Omar,Sumera Dero,3, Yuming Chu, Ilyas Khanand Kottakkaran Sooppy Nisar

1School of Quantitative Sciences, Universiti Utara Malaysia, 06010,Sintok, Kedah, Malaysia

2KCAET Khairpur Mir’s, Sindh Agriculture University, Tandojam Sindh,70060, Pakistan

3IICT, University of Sindh,Jamshoro, 76080, Pakistan

4Department of Mathematics, Huzhou University, Huzhou, 313000,China

5Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, Changsha University of Science &Technology, Changsha, 410114,China

6Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

7Department of Mathematics,College of Arts and Sciences,Prince Sattam bin Abdulaziz University,Wadi Aldawaser,Saudi Arabia

Abstract: The unsteady magnetohydrodynamic(MHD)flow on a horizontal preamble surface with hybrid nanoparticles in the presence of the first order velocity and thermal slip conditions are investigated.Alumina (Al2O3) and copper (Cu)are considered as hybrid nanoparticles that have been dispersed in water in order to make hybrid nanofluid(Cu-Al2O3/water).The system of similarity equations is derived from the system of partial differential equations (PDEs) by using variables of similarity, and their solutions are gotten with shooting method in the Maple software.In certain ranges of unsteadiness and magnetic parameters, the presence of dual solutions can be found.Further,it is examined that layer separation is deferred due to the effect of the hybrid nanoparticles.Moreover,the capacity of the thermal enhancement of Cu-Al2O3/water hybrid nanofluid is higher as compared to Al2O3/water based nanofluid and enhancements in ϕCu are caused to rise the fluid temperature in both solutions.In the last, solutions stability analyzes were also carried out and the first solution was found to be stable.

Keywords: Cu - Al2O3/H2O; hybrid nanofluid; magnetic field; slip conditions;dual solutions

1 Introduction

The topic of research in various engineering and industrial fields, such as air-conditioning,microelectronic, and power generation is energy sustainability and the optimizations of thermal systems performance.For energy sustainability, an inventive variety in thermodynamics was important [1].Throughout such engineering processes, the cooling systems operate on a fluid medium through a forced flux in the absence and presence of convective heat transfer.The thermal conductivity of the liquid is therefore worthwhile to be enhanced for a better engineering process.The nanofluid formation is created through scattering single nanoparticle into the normal fluids, for example, vegetable oil, glycol, water, or the combination of glycol with water.The nanoparticles can be classified as carbon (CNTs, MWCNT),metal oxides (Al2O3,Fe2O3,CuO), metal (Cu, Ag), and metal carbide and nitride.Many researchers dealt with the various kind of nanoparticle combinations for example metal oxides (Al2O3, CuO), metals (Al,Cu, Fe), and semiconductors (SiO2,TiO2) nanoparticles.The important references on nanofluid can be seen in the books of [2,3].On the other hand, comprehensive review papers on the nanofluid were written by[4-12].

Recently, researchers introduced a new type of nanofluid, and they call it Hybrid nanofluid.Hybrid nanofluid helps the regular nanofluids to improve its thermal properties.It can be described as the hybrid nanofluid, which consists of two different kinds of nanoparticles together with new chemical and thermophysical properties that can improve the rate of heat transfer due to synergistic properties (see[13]).Esfe et al.[14] stated that the good heat transfer rate is gotten by hybridizing the small amount of the nanoparticles volume fraction in the base fluid.Yan et al.[15] stated that the rate of heat transfer of the hybridized nanofluid is more as compared to the normal water-based nanofluid during the examination of the Cu-Al2O3/water nanofluid.They found ranges of the existence of multiple solutions and also performed stability analysis of the solutions.Lund et al.[16] examined the MHD flow of Cu-Fe3O4/H2O hybrid nanofluid over non-linear stretching and shrinking parameters in the presence of the joule heating.Two solutions were found, and an unstable solution was recognized by without doing stability analysis due to the existence of the singularity in the second solution.Further, Waini et al.[17]obtained two solutions during the examination of the hybrid nanofluid over vertical sheet embedded in a permeable medium.They claimed that the non-uniqueness of solutions depends on the ranges of the mixed convection parameter.Waini et al.[18] continued the problem of [19] for the hybrid nanofluid and successfully found dual solutions in the ranges of the unsteadiness parameter.Due to various practical applications of the unsteady flow, the research of [19] was also extended by the [20] for the nanofluid by using of the double phase model and successfully found the dual solutions.The same paper was also extended by the [21] for the MHD unsteady flow of the Casson type nanofluid with effects of the slip conditions and Stefan blowing and noticed that dual solutions are also possible for the accelerated surface.Further, Lund et al.[22] considered the revised model of [18,19] for the unsteady incompressible MHD flow of the hybrid nanofluid in the existence of thermal radiation effects.It is now clear the importance of the unsteady model for the practical point of view.In this paper, we also extended the work of [18] and [22] for the hybrid nanofluid in the absence of the viscous dissipation and thermal radiation effect.To date, numerous review publications are present in the literature on the synthesis and preparation and hybrid nanofluids, such as [23-30].Besides, some significant research articles of hybrid nanofluids are also available in these references[31-38].

The main objective of the current article is,therefore,to extend the works of[18,22]of MHD flow of the hybrid nanofluid on a shrinking sheet with the effect of the magnetic field, velocity, and thermal slip conditions.The alumina (Al2O3) and copper (Cu) are known to be hybrid nanoparticles here.The nanoparticles are then dispersed in order to develop the hybrid nanofluid (Cu-Al2O3/water).In order to validate the present results,current results are compared with the results of the previously published.

2 Mathematical Formulation

Let us take the MHD unsteady flow ofCu-Al2O3/water hybrid nanofluid over the shrinking sheet.The coordinate system and the physical representation of the problem are shown in Fig.1.Further,velocity and thermal partial slip conditions are also taken into account wherevw(x)=is the mass transfer.Besides, the flow is assumed to be subject to a transverse magnetic field =where constant magnetic field isB0.The infulence ofBon the shrinking sheet is applied perpendicular (see Fig.1).Tiwari and Das’s model are expressed as follows based on the considered assumptions[18,22]:

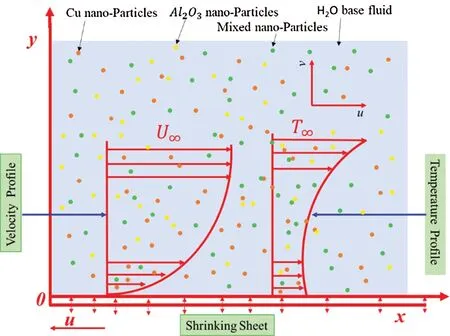
Figure 1:Physical models and coordinate systems

The subject to boundary conditions[21]

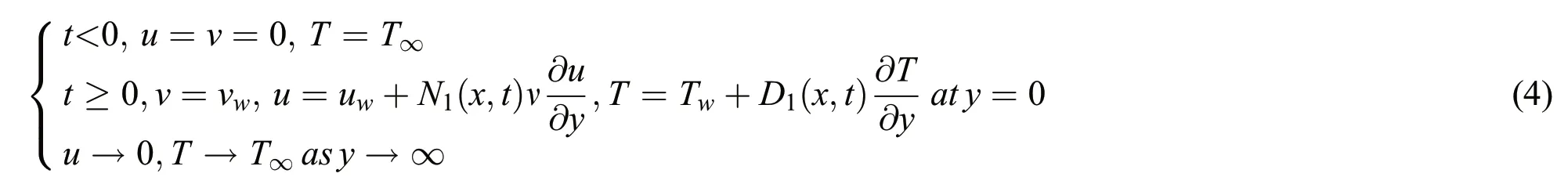
where velocity of surface isuw(x,t)=followed in the present analysis.The thermophoresis property of Yan et al.[15] are

Further,N1(x,t)=is velocity slip factor andD1(x,t)=is thermal slip factor whereN0andD0are the slip factors.Tabs.1 and 2 demonstrate these features of hybrid nanofluid.

We employ the following variable of similarity transformation to convert the Eqs.(1)-(3)into a system of ODEs.

Table 1:Thermophysical properties of hybrid nanofluid[22]

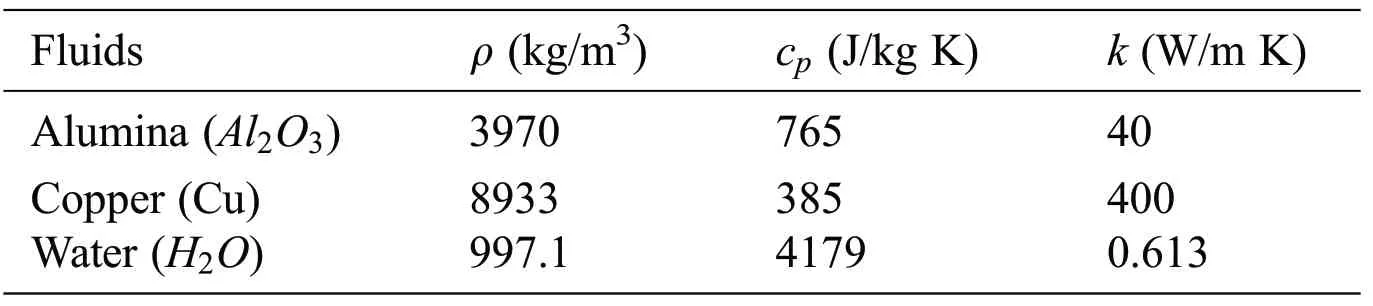
Table 2:The thermo physical properties of the base fluid (water) and the nanoparticles [18,22]

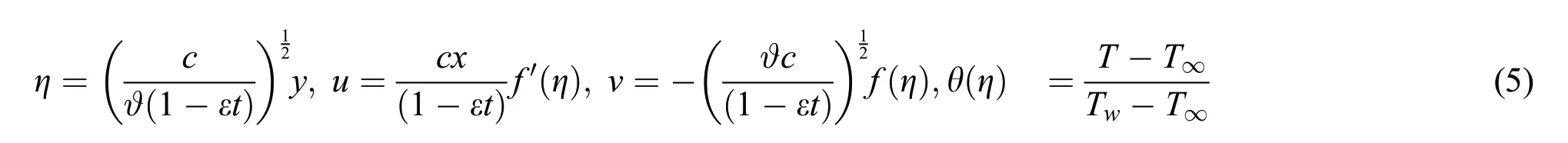
By applying Eq.(5)into Eqs.(1)-(3)then we have following non-dimensional form of ODEs

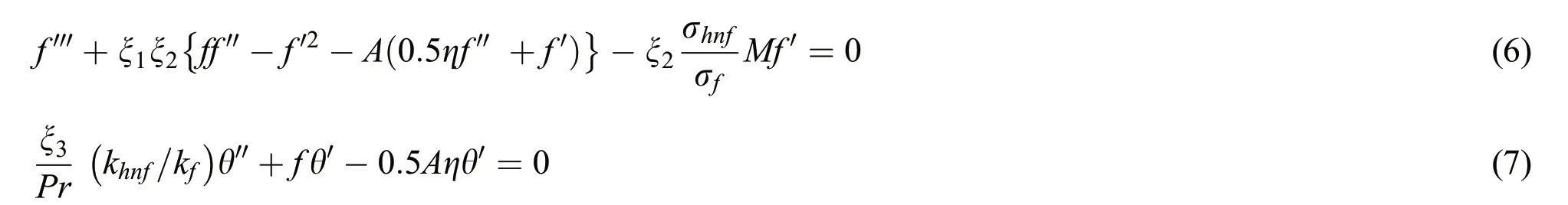
Along with the boundary conditions

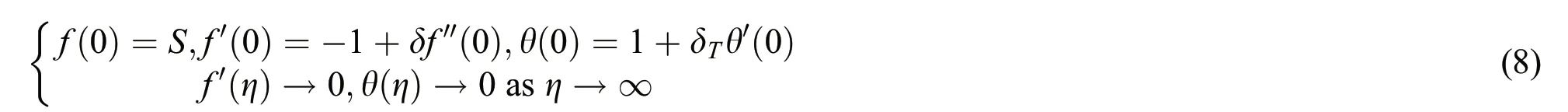
The non-dimensional quantities are given as

The coefficient of skin frictionCfand local Nusselt numberNuxare given as

By employing Eq.(9)in Eq.(10),we get

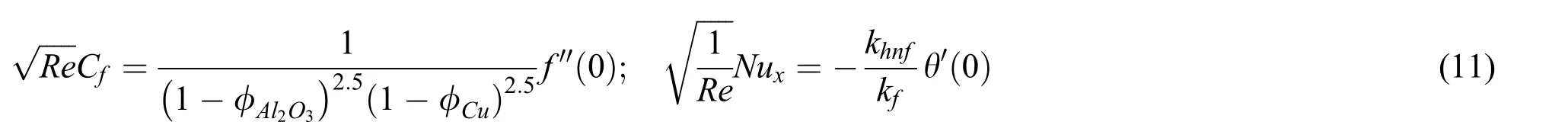
whereReis local Reynold number.

3 Stability Analysis

Merkin et al.[39-43] suggested for the stability analysis that the new non-dimensional variables of similarity transformation need to be introduced by considering τ=therefore, following new similarity transformation variables are introduced.

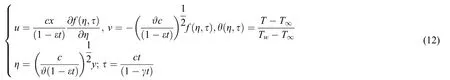
By putting Eq.(12) in Eqs.(2) and(3), we get

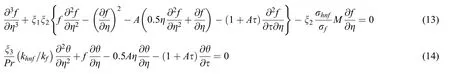
Along with boundary conditions

According to Lund et al.[41], “to check the stability of steady flow solutions wheref(η )=f0(η ),andθ(η )=θ0(η )of satisfying the boundary value problem Eqs.(6)-(8)”,we have

whereF(η ) andG(η ) are relatively small tof0(η ) and θ0(η ) and Y is called as unknown parameter of eigenvalue which need to be determined.Thus, we have the following linearized problems of eigenvalue,by replacing Eq.(16) in Eqs.(13)and (14) with τ=0.

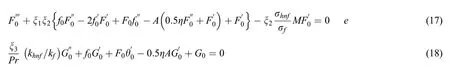
Subject to the boundary conditions

According to Dero et al.[44-46], one boundary condition from two should be converted to initial boundary condition (relaxed) in order to achieve the smallest values of eigenvalue.Therefore,is relaxed into

4 Results and Discussion

The shooting method in Maple code with add of shootlib function has been employed to solve unsteady flow equations and bvp4c code in MATLAB software is used to solve the normalizing stability equations.The results of these codes are compared graphically and numerically with previously published works and found in the excellent agreements.In this study, η∞=4 is kept fxied during the computations but it is also noticed that η∞=1 and η∞=3 are tolerable for temperature and velocity profiles in order to satisfy the η →∞as shown in Figs.9 and 10, respectively.For the numerical compression, Tab.3 is construction for the magnitude off′′(0 ) and -θ′(0 ) with previously available results of [22].It is found that our results are showing a favorable agreement.Further, it can be observed from Tab.4 that the first(second) solution is stable (unstable) as the values of γ are positive (negative).The positive (negative)magnitude of γ should be noted as indicating an initial decay (growth)of disturbance.

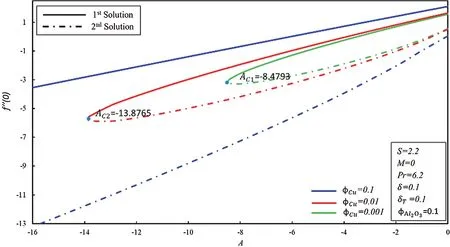
Figure 2:Conmparison with the 6th Fig.of [18]

The preparation of a hybrid nanofluid has been shown in the studies of [15,17,22].They originally considered nanoparticles of alumina (Al2O3) into water base fulid and then, nanoparticles of copper (Cu)were mixed with the alumina (Al2O3) by considering the distant fractions of solid volume in order to make a hybrid nanofluid.This kind of hybrid nanofluid was called asCu-Al2O3/water.We also follow their works by keeping the=0.1 as constant in the whole article while the range of 0.001 ≤ϕCu≤0.1 was kept for copper nanoparticles.

Table 3:Values of f ′′ (0 )and θ′ (0 )for Cu-Al2O3/H2O hybrid nanofulid for A when M =δ=δt =0,S =2.1,Pr=6.2,ϕCu =0.2 and ϕAl2O3 =0.1

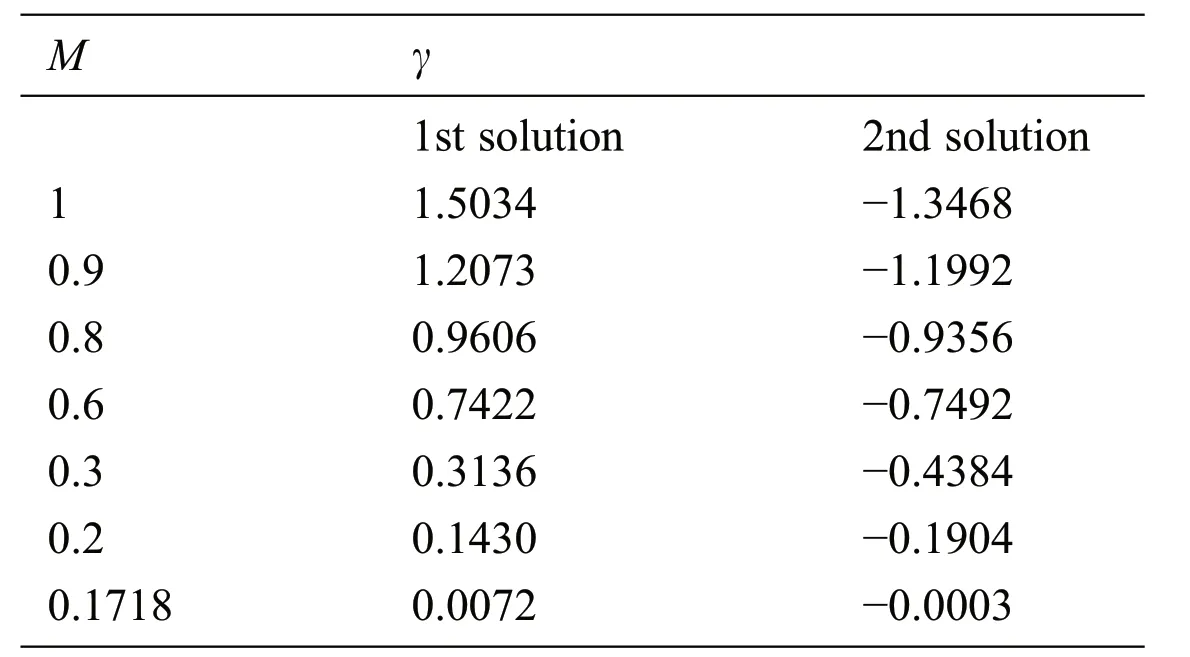
Table 4:The smallest eigenvalues γ for the numerous values of magnetic parameter M at ϕCu = ϕAl2O3 =0.1S =2, Pr=6.2, δ=δT =0.1 and A=-5

We have water as a base fluid so Pr = 6.2 is kept as constant for the room temperature of 25°C.The graphical contrast with the sixth graph of [18] is demonstrated in Fig.2 in order to validate our numerical coding and its results.It can be concluded that our numerical coding is working properly and can be used in this study as the critical values of our figure is the same as given in the article of [18].

Figs.3 and 4 display the coefficient of skin frictionf′′(0 ) and rate of heat transfer -θ′(0 ) ofCu-Al2O3/water nanofluid toMfor numerous estimations of ϕCu, respectively.Range of first and second solutions isM≥Mciwherei=1,2,3, whereas range of no solution isM＜MciwhereMcishows the critical values of magnetic field for respective ϕCu=0.001, 0.01, 0.1.

It should be noted that at the pint ofMci,fluid flow of boundary layer initiates converting from laminar flow to turbulent flow and it is noticed from the previous studies that this is possible only when fluid is flowing over the shrinking surface.Further, it is observed that dual solutions exist when the flow is deaccelerated which means that values of the unsteadiness parameter are negative.Moreover, the rate of heat transfer increases in the first solution for the rising effect of the magnetic field, while it decreases in the second solution.

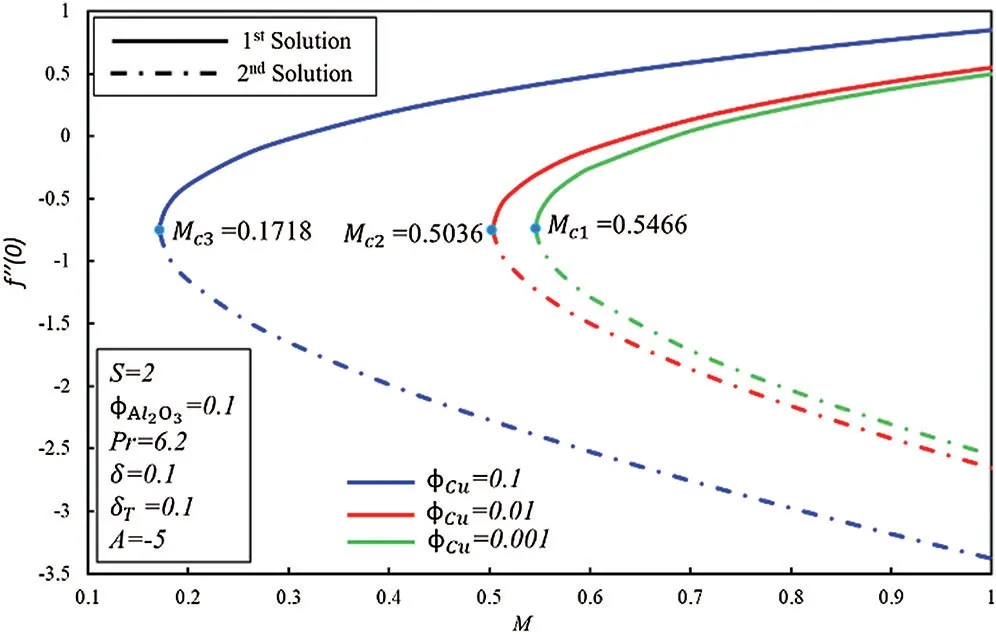
Figure 3:Variation of f″ (0)for ϕCu along with various values of M

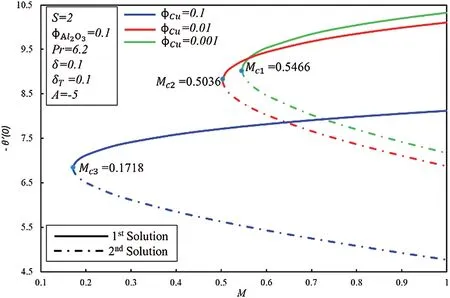
Figure 4:Variation of -θ′(0)for ϕCu along with various values of M

Figs.5 and 6 show the significance of unsteadiness parameterAfor different values of suction parameterSonf′′(0 ) and -θ′(0 ), respectively.The coefficient of skin frictionf′′(0 ) improves in the first solution as suction increases, whereas it decreases in the second solution.The enhancement in thef′′( 0) is since suction generates the drag force inside the boundary layer.At the same time, the skin friction coefficient increases in both solutions as the unsteadiness parameter increases.Decreasing and increasing behavior of heat transfer rate observed in two solutions as unsteadiness parameter enhances.Further, the rate of heat transfer enhances in the first solution as suction increases, while dual nature is observed in the second solution.

Variations off′′(0 ) against velocity slip factor δ for numerous values ofAis revealed in Fig.7.It is noticed that the dual solutions can be found in a specific range ofAwhich isAc≥A, while no solution is obtained asAc＜A, whereAcis known as the critical points where existences of solutions are possible.It is perceived that the presence of slip effect delay the boundary layer separation whereAc2=-6.7138 andAc2=-5.8118 are the critical values of the δ=0.1 and δ=0.2, respectively.At the same time,magnitudes off′′(0 ) increase when δ ＞0 in the second solution, whereas there exist dual behaviors in the second solution.Fig.8 demonstrates the variation of -θ′(0 ) versus thermal slip condition δTfor many values ofA.It can be detected that dual behavior is noticed in the magnitude of the rate of heat transfer in the first solution as thermal slip condition δTis enhanced, while the rate of heat transfer declines in the second solution when δTincreases.It is also noticed that δT=0,0.1,0.2 has the same critical value which means that increments in the thermal slip do not affect boundary-layer separation.

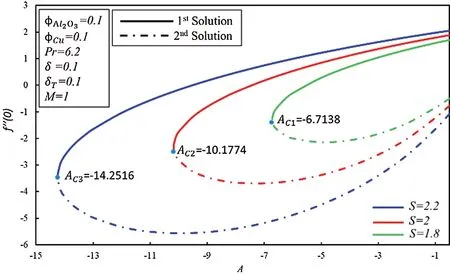
Figure 5:Variation of f″(0) for S along with various values of A

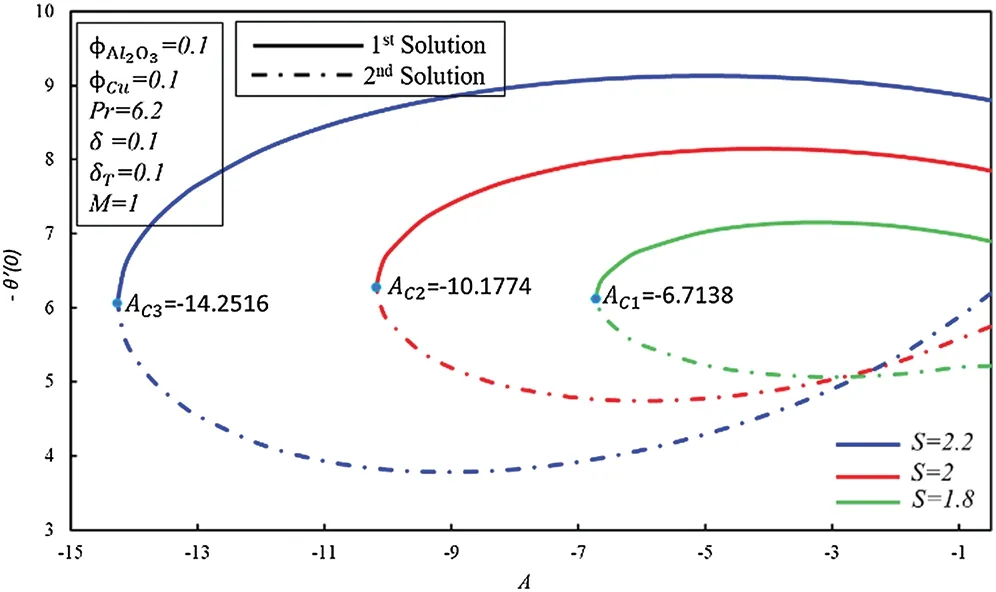
Figure 6:Variation of-θ′(0)for S along with various values of A

Effects of ϕCuon profiles of velocityf′(η ) and temperature θ(η ) are illustrated in Figs.9 and 10,respectively.In comparison, the capacity of the thermal enhancement ofCu-Al2O3/water hybrid nanofluid is more toAl2O3/water-based nanofluid.

It is gained that fluid velocity declines in the first solution as ϕCuenhances and as a resulting thickness of the hydrodynamic layer decreases.After all, velocity increases at first and then starts to decrease in the second solution.Further, enhancements in ϕCuare caused to raise the temperature of the fluid in both solutions as shown in Fig.10.

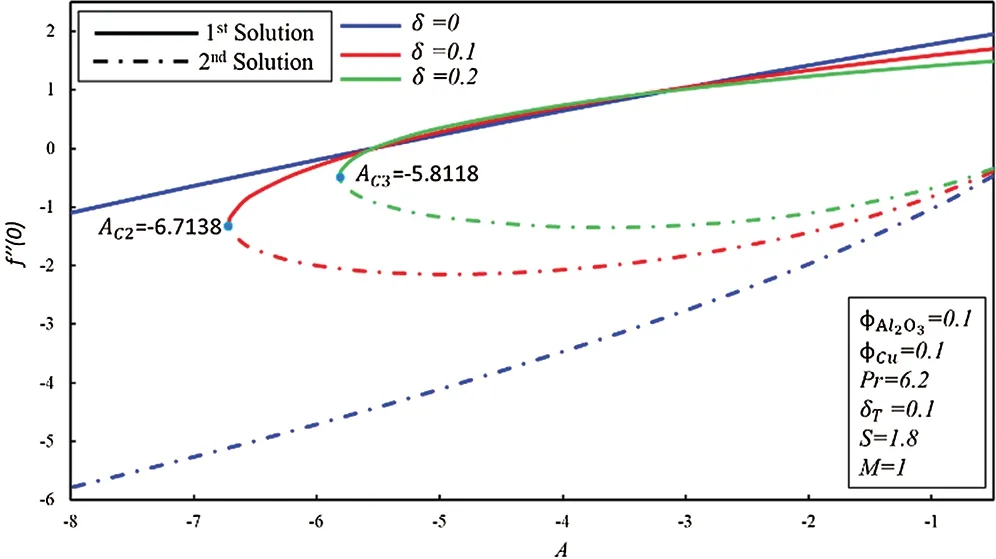
Figure 7:Variation of f″(0) for δ along with various values of A

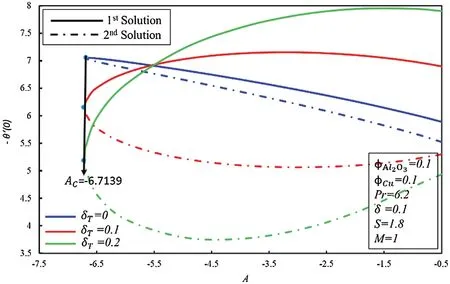
Figure 8:Variation of -θ′(0) for δ T along with various values of A

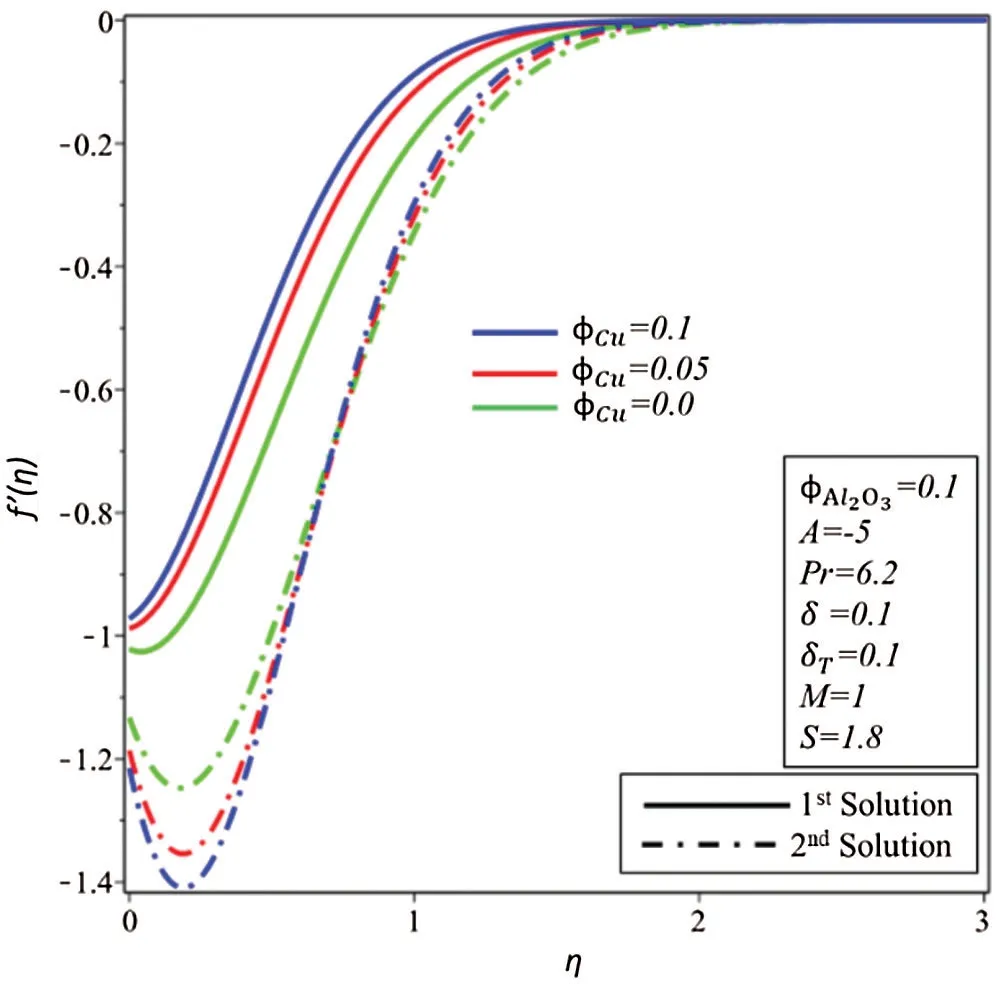
Figure 9:Variation of f″ (η) for φCu

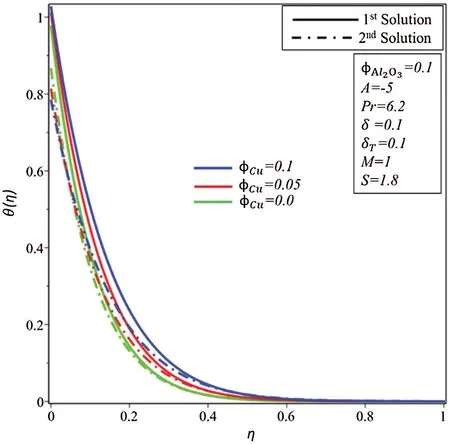
Figure 10:Variation of θ (η)for φCu

5 Conclusion

In the current examination,the papers of[18,22]are extended in order to inspect the effects of MHD and slip for a hybrid nanofluid case.The current findings were checked for verification with previously reported data and an agreement between those findings is outstanding.Dual solutions have been found in some ranges of magnetic and unsteadiness parameter.The range of the first and second solutions isM≥Mciwherei=1,2,3, whereas range of no solution isM＜MciwhereMcishows magnetic critical values for respective values of ϕCu=0.001, 0.01, 0.1.Further, the magnitude of the rate of heat transfer is increased in the first solution as thermal slip condition δTis enhanced, while the heat transfer rate declines in the second solution as δTincreases.The coefficient of skin frictionf′′0( ) enhances in the first solution as suction increases, while it decreases in the second solution.Stability analyzes are carried out and the results suggest that the first solution is stable.

Funding Statement:This project was supported by the Natural Science Foundation of China (Grant Nos.61673169,11701176,11626101,11601485).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.