Path Planning of Quadrotors in a Dynamic Environment Using a Multicriteria Multi-Verse Optimizer

Raja Jarray,Mujahed Al-Dhaifallah,Hegazy Rezk and Soufiene Bouallègue,5

1Research Laboratory in Automatic Control(LARA),National Engineering School of Tunis(ENIT),University of Tunis El Manar,Tunis,1002,Tunisia

2Department of Systems Engineering,King Fahd University of Petroleum&Minerals,Dhahran,31261,Saudi Arabia

3College of Engineering at Wadi Addawaser,Prince Sattam Bin Abdulaziz University,Al-Kharj,11911,Saudi Arabia

4Department of Electrical Engineering,Faculty of Engineering,Minia University,Minia,61517,Egypt

5High Institute of Industrial Systems of Gabès(ISSIG),University of Gabès,Gabès,6011,Tunisia

Abstract:Paths planning of Unmanned Aerial Vehicles(UAVs)in a dynamic environment is considered a challenging task in autonomous flight control design.In this work,an efficient method based on a Multi-Objective Multi-Verse Optimization(MOMVO)algorithmis proposed and successfully applied to solve the path planning problem of quadrotors with moving obstacles.Such a path planning task is formulated as a multicriteria optimization problem under operational constraints.The proposed MOMVO-based planning approach aims to lead the drone to traverse the shortest path from the starting point and the target without collision with moving obstacles.The vehicle moves to the next position from its current one such that the line joining minimizes the total path length and allows aligning its direction towards the goal.To choose the best compromise solution among all the non-dominated Pareto ones obtained for compromise objectives,the modified Technique for Order Preference by Similarity to Ideal Solution(TOPSIS)is investigated.A set of homologous metaheuristics such as Multiobjective Salp Swarm Algorithm(MSSA),Multi-Objective Grey Wolf Optimizer(MOGWO),Multi-Objective Particle Swarm Optimization(MOPSO),and Non-Dominated Genetic Algorithm II(NSGAII)is used as a basis for the performance comparison.Demonstrative results and statistical analyses show the superiority and effectiveness of the proposed MOMVO-based planning method.The obtained results are satisfactory and encouraging for future practical implementation of the path planning strategy.

Keywords:Quadrotors;path planning;dynamic obstacles;multi-objective optimization;global metaheuristics;TOPSIS decision-making;Friedman statistical tests

1 Introduction

In the last decades,unmanned aerial vehicles have acquired a great potential to complete an autonomous or semi-autonomous mission.A growing number of applications have appeared in real-world environments [1,2].To achieve this autonomy,several challenges must be met.The trajectory planner is an essential part of the UAV autonomous control process [3].Vehicles’trajectory planning is used to find a sequence of valid moves that allow a robot to move from an initial state to the desired end state.In general,a valid movement is a displacement that does not produce a collision and that respects the kinematic constraints of the robot [4].In some planning problems,the location of obstacles can change over time.Thus,trajectory planning must respect the dynamic constraints that arise from the environment,i.e.,mobile obstacles,and the considered specifications of the vehicles.Besides,most real path planning problems need to be solved by considering different conflicting goals such as price and quality.The trajectory planning problem is then considered as a Multi-Objective Optimization Problem (MOOP).

Many researchers have carried out various works to solve the Multi-Objective Path Planning(MOPP) problem for UAVs in a dynamic environment.The authors in [5]proposed a new methodology based on an Improved Gravitational Search Algorithm (IGSA) to solve the path planning for multi-robots in a dynamic environment.In [6],the authors investigated a new algorithm for UAV path planning problems based on Ant Colony Optimization (ACO) and artificial potential field.In [7],a Pigeon-Inspired Optimization (PIO) algorithm is used to optimize the initial path and another Fruit Fly Optimization Algorithm (FFOA) is used to solve the global path planning problem in a three-dimensional dynamic environment of oilfields.The authors in [8]proposed a novel Predator-Prey Pigeon-Inspired Optimization (PPPIO) to solve the Uninhabited Combat Aerial Vehicle (UCAV) 3D path planning problem in a dynamic environment.In [9],a novel integrated path planning approach based on an A* algorithm and local trace-back model has been proposed to solve such kind of hard problems.The authors in [10]developed an Improved Artificial Bee Colony (IABC) algorithm to solve the path planning problem in an environment of dynamic threats thanks to its fewer control parameters and faster convergence.

Although these works have been developed to solve the MOPP problem for a UAV flying in a dynamic environment,most of them converted the multi-objective problem into a single objective problem by using a weighted sum function [11].This technique is easy to implement,but it is difficult to determine the best weights for the various contradictory objectives.The bias will be enjoined throughout the optimization process.Other methods have been developed to deal with the MOPP problem and obtain a set of optimal Pareto solutions.These methods can be classified into two types:exact methods and approximate methods [12].An exact method such as Multi-Objective Branch &Bound (MOBB) is used to get the best solutions in the Pareto Optimal Frontier (POF) for the given path planning problem [13].However,the computational complexity is highly elevated.The approximate multi-objective optimization methods are thus developed and used extensively in recent years to solve the MOOP.The path planning problem for UAVs in a dynamic environment is no exception.In [14],the path planning problem in an uncertain and dynamic environment is considered as a constrained multi-objective optimization problem with uncertain coefficients which is solved using a constrained Multi-Objective Particle Swarm Optimization (MOPSO) technique.In [15],a Modified Central Force Optimization (MCFO) based technique is introduced to solve the path-planning problem for a 6 DOF rotary-wing quadrotor helicopter.In such work,the theory of the Particle Swarm Optimization (PSO) and the mutation operator of the Genetic Algorithm (GA) are combined to improve the original CFO method.

In the above-mentioned studies,the idea of using multi-objective metaheuristics for path planning problem’s formulation and the resolution seems a promising solution.To overcome the limits and inconveniences of the cited methods,particularly in terms of complexity and prohibitive time consuming,a systematic and efficient path planning method is proposed based on an advanced Multi-Objective Multi-Verse Optimization (MOMVO) algorithm.The main contributions of this paper are summarized as follows:1) a novel strategy of reformulation and solving of a MOPP problem under operational constraints in a dynamic environment is proposed based on the concepts of the multi-criteria multi-verse optimization.Such a planning strategy allows guiding the quadrotor UAV to ensure destination position by calculate the next position in each step time while avoiding all moving obstacles.2) A modified TOPSIS is employed as a higher-level decisionmaking approach to choose the best compromise solution among all the non-dominated solutions in the sense of Pareto.3) A nonparametric statistical analysis method is proposed to compare all reported solvers for the hard path planning problem.

The remainder of this paper is organized as follows.In Section 2,the path planning problem for a quadrotor UAV is formulated as a multi-objective optimization problem under operational constraints.Section 3 presents the proposed multi-objective multi-verse optimizer to solve the formulated path planning problem.Section 4 describes the dynamical model of the studied quadrotor and the PID control design for the position and attitude dynamics stabilization and tracking.In Section 5,demonstrative results and comparisons are carried out and discussed.Section 6 concludes this paper.

2 Path Planning Problem Formulation

The quadrotor passed from the starting point A(x1,y1,z1)to the target one B(xn,yn,zn).The x-axis range(x1,xn)is divided inton-1 equal segments and defined asx1,x2,x3,...,xn.The time is incremented,the quadrotor has moved from positionwi=(xi,yi,zi)to the next positionwi+1=(xi+1,yi+1,zi+1)where the positions {xi}1≤i≤nare selected and the decision variables for optimization are defined asθ={yi+1,zi+1},∀i=1,2,...,n-2.

In the UAVs’path planning formalism,the length of the flight path is very important.In this work,the robot determines its next position from its current one and tries to align its direction towards the goal.Consider initially,the UAV placed in the location at a timetin the space coordinate(xi,yi,zi).At the time(t+Δt),it wants to move to the next position(xi+1,yi+1,zi+1)such that the line joining between {(xi,yi,zi),(xi+1,yi+1,zi+1)} and {(xi+1,yi+1,zi+1),(xn,yn,zn)}minimizes the total path length and allows the UAV to align its direction towards the goal.So,the first proposed objective function of the multi-objective optimization problem,denoted asf1,is defined as follows:

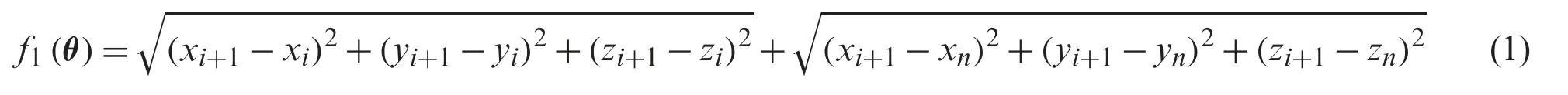
Besides,the path planning process cannot totally ignore the dynamic characteristics of the UAV.When the UAV moves in the straighter path,the burden of the control system is reducing and the fuel cost of the flight process is decreasing [16].The second objective functionf2is thus defined as follows:

On the other hand,avoidance of obstacles in a dynamic flight environment is more complex than in a static one.To simplify the characterization of moving obstacles,they can be modeled by spheres of radiusRand centerc.Thus,at the beginning of the program,the center,radius,and velocity vector of such spheres are initialized.At each time stepΔt,the positions of a given moving obstacle are updated as:

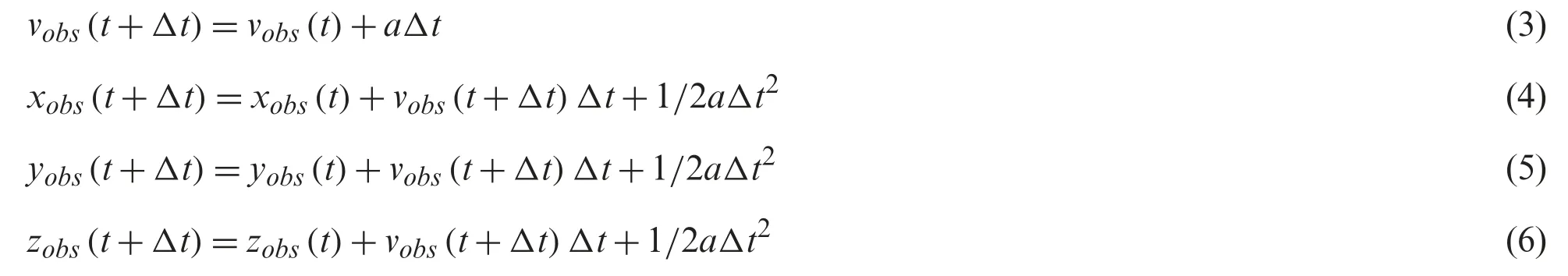
wherevobsis the velocity of a dynamic obstacle,andais its acceleration.

When the UAV moved from the actual position(xi,yi,zi)to the next position(xi+1,yi+1,zi+1),it does not intersect any obstacle.So,it should be tested if any obstacle intersects the line segment connecting the two positions.The line through(xi,yi,zi)and(xi+1,yi+1,zi+1)can be written as:

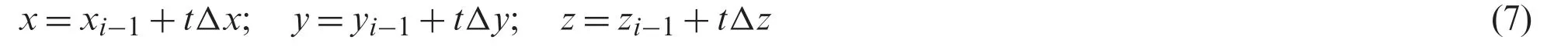
whereΔx=xi-xi-1,Δy=yi-yi-1,andΔz=zi-zi-1denote the increments on the drone’s positions.

The equation of a given sphere with the center’s coordinates(xc,yc,zc)is written as follows:

Then,substituting Eq.(7) into Eq.(8) leads to the following equation:

whereA,B,andCterms are defined as follows:

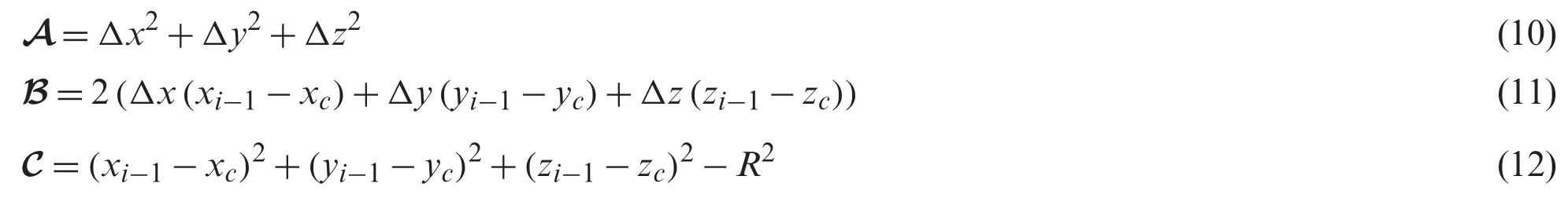
As explained in [17],the solving of Eq.(9) can give an idea of the intersection or not of the drone path with the considered moving obstacles.Indeed,when the discriminateDjof Eq.(13)is negative there are no intersections with the obstacles:

wherej=1,2,...,m,andm∈N is the number of moving obstacles.

Finally,the formulated multi-objective optimization problem for the path planning of the quadrotor UAV according to a given ithwaypoint is defined as follows:

wheref1(.),f2(.),andgj(.)=Dj(.)are the cost and constraint functions given by Eqs.(1),(2),and (13),respectively,θ={yi+1,zi+1}is the decision variables andis the bounded research space.

To handle the inequality constraints of the problem (14),the following external static type of penalty function is used as follows [18]:

whereμj∈R+is the jthpenalty parameter associated with the jthconstraint,nconis the total number of the inequality constraints,andk∈{1,2}.

3 Proposed Path Planning Algorithm

3.1 Multi-Objective Multi-Verse Optimizer

Originally proposed by Mirjalili et al.[19],the Multi-Verse Optimizer (MVO) is a populationbased metaheuristic inspired by the physics theory of the existence of multi-verse.In this formalism,the interaction among different universes is ensured based on the concepts of white/black holes and wormholes.The main motion equations of the MVO metaheuristic are given as follows [19]:

wherexjidenotes the jth component in the ithsolution,xjis the jth variable of the best universe,lbjandubjare the lower and upper bounds,respectively,r2,r3,andr4are random numbers in the interval [0,1].

In Eq.(16),the termsTDRandWEPpresent the traveling distance rate and the wormholes’existence probability,respectively,and are defined as follows:

whereρminandρmaxare the wormhole existence probabilities,iteris the current iteration,andγdefines the exploitation accuracy.

To develop a multi-objective version of the MVO metaheuristic for the problem (14),a concept of the archive is investigated.The leader selection and roulette wheel approaches are used to select the fittest solutions according to the following probabilistic mechanism [20]:

whereϑidenotes the number of the vicinity solutions andα＞1 is a constant.

Based on the above motion equations and the archive updating mechanism (19),a pseudocode of MOMVO is given by Algorithm 1.

Algorithm 1:MOMVO Step 1:Set the control parameters of MOMVO algorithm.Step 2:Randomly initialize the population,i.e.,the positions of universes.Step 3:While (iter＜Max_iter+1) do Update WEP and TDR by applying Eqs.(17) and (18).For each universe do Boundary checking for the universes inside search space.Calculate the inflation rate (fitness) of universes.End For Sort the fitness values Find the non-dominated solutions.Normalize the inflation rates of each universe.Update the archive regarding the obtained non-dominated solutions.If the archive is full do Delete some solutions from the archive to hold the new.End if Update the position of universes according to Eq.(16).If any new added solutions to the archive are outside boundaries do Update the boundaries to cover the new solution(s).End if Increment iter Step 4:Stop the algorithm’s execution when it reaches Max_iter.

3.2 Decision-Making Model

The selection of an optimal solution requires in particular a higher-level decision-making approach.The modified TOPSIS method is used to choose with more safety the best compromise solution among all the non-dominated ones in the sense of Pareto.Such a multiple-criteria decision-making approach is implemented as follows [21]:

Step 1:Obtain the decision matrix

Step 2:Normalize the decision matrix

Step 3:Find the positive-and negative-ideal solutions

Step 4:Calculate thew-dimensional weighted Euclidean distances

Step 5:Calculate the relative closeness to the ideal solution

Step 6:Choose an alternative with maximumCi

4 Tracking of the Planned Paths

4.1 Dynamic Model

The basic movements of the quadrotor are realized by varying the speed of each rotor as shown in Fig.1.To evaluate the mathematical model of the quadrotor,two coordinate systems have been used,i.e.,earth reference frameFe(Oe,xe,ye,ze)and body-fixed frameFb(Ob,xb,yb,zb).

Figure 1:Quadrotor prototype and its related frames

The studied quadrotor is presented with its translationalξ=(x,y,z)Tand rotationalη=(φ,θ,ψ)Tcoordinates.Let a vectorϑ=(p,q,r)Tdenotes the angular velocity of the drone in the body-frame.Using the Newton-Euler formalism,a dynamic nonlinear model is given as follows [22-24]:

where-π/2≤φ≤π/2,-π/2≤θ≤π/2,and-π≤ψ≤πare the roll,pitch,and yaw Euler angles,respectively,mQdenotes the mass of the quadrotor,gis the gravitational acceleration,Jris the z-axis inertia of the propellers,Ix,IyandIzdenote the inertias of the quadrotor,κ1,2,...,6are the aerodynamic friction and drag coefficients,andωr=ω1-ω2+ω3-ω4is the overall residual rotor angular velocity.

The control inputsu1,u2,u3andu4are defined as follows:

wherebandddenote the lift body and drag propellers coefficients,respectively,ldenote the distance from the center of mass to each motor.

4.2 Tracking PID Controllers’Design

The proposed control system of the quadrotor UAV is shown in Fig.2.Such a control scheme is composed of an inner-loop attitude controller and an outer-loop position controller.The two controllers are designed with the classical PID structure as follows:

whereeis the tracking error between the desired reference and the accessible system output,KP,KI,andKDare the proportional,integral,and derivative gains of the PID controller,respectively.Two cascade loops for decoupling control of all flight dynamics are investigated.An inner loop is set to ensure the attitude and heading’s tracking.And the outer loop is designed for the positions(x,y)and altitudezdynamics [25].The desired trajectories for the attitude variablesφdandθdare generated from Eqs.(28) and (29) shown as virtual control laws for the translational dynamics [26-28]:

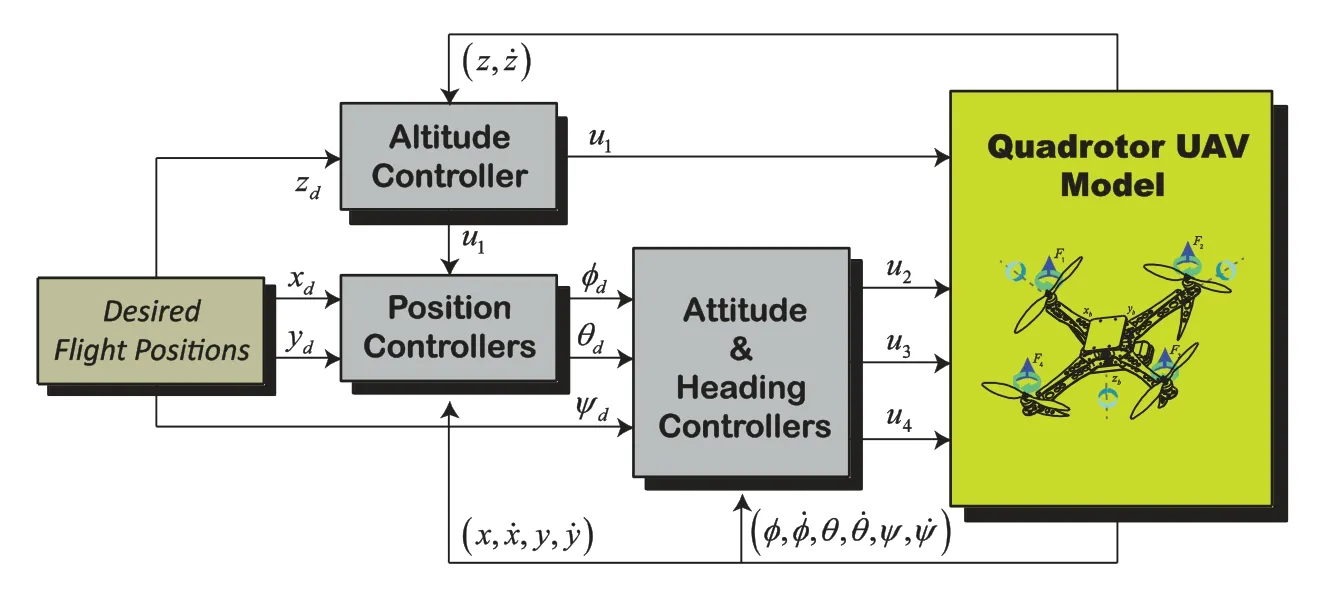
Figure 2:Full control scheme of the quadrotor

Solving Eqs.(28) and (29) for a given yaw angleψleads to the desired roll and pitch angles’formula respectively given as follows:

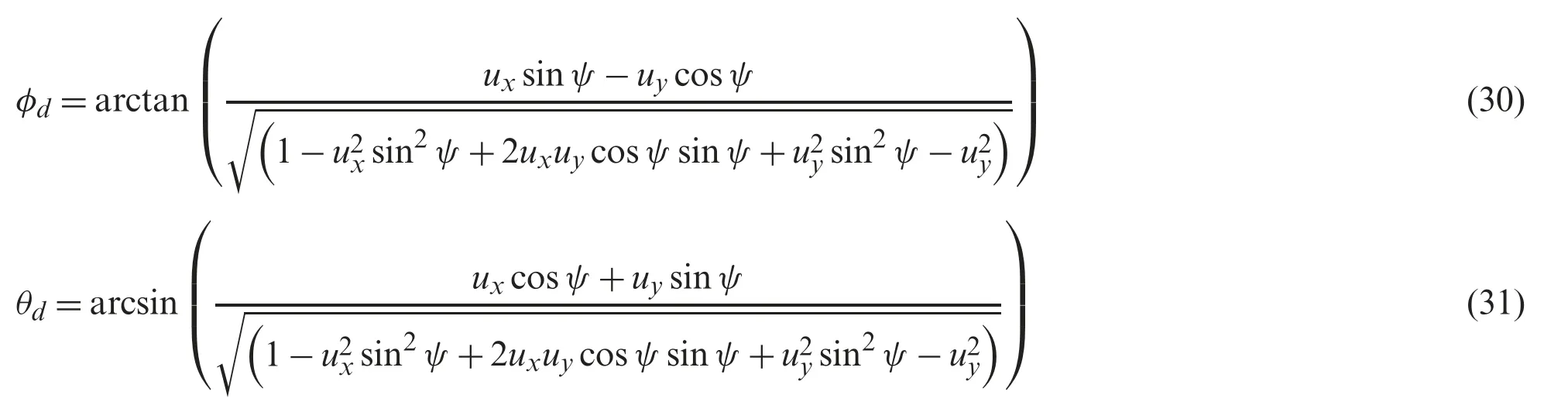
5 Simulation Results and Discussion

To illustrate the performance of the proposed MOMVO-based method,a 3D dynamic environment with moving obstacles is developed under the MATLAB/Simulink software.An interactive Graphical User Interface (GUI) has been implemented for the different simulations.The quadrotor’s 3D trajectory can be viewed by designing an animated quadrotor that receives the simulation data and performs the dynamical responses.Some performance index values,such as path length,flight time,and response plots of the quadrotor along the X,Y,and Z-axis,are presented and discussed.In this study,the quadrotor’s physical parameters are given in Appendix A.Tab.1 gives the different flight scenarios considered in the dynamic environment.

To compare the performance of the proposed MOMVO-based planning method,others algorithms such as MSSA,MOGWO,MOPSO,and NSGAII are retained.The control parameters of such optimizers are summarized in Tab.2.

To have a fair and reliable comparison,the common parameters such as the maximum number of iterations and the population size are set as 100 and 50,respectively.For statistical comparison purposes,all algorithms are independently executed 10 times and compared in the sense of the solutions’quality.In each step time,the quadrotor calculates the next position by solving the formulated multi-objective optimization problem (14) based on a multi-objective optimization algorithm.The execution of the reported algorithms leads to obtain a set of non-dominated solutions as shown in Fig.3.These Pareto fronts are considered at the first time-step to have a fair comparison.

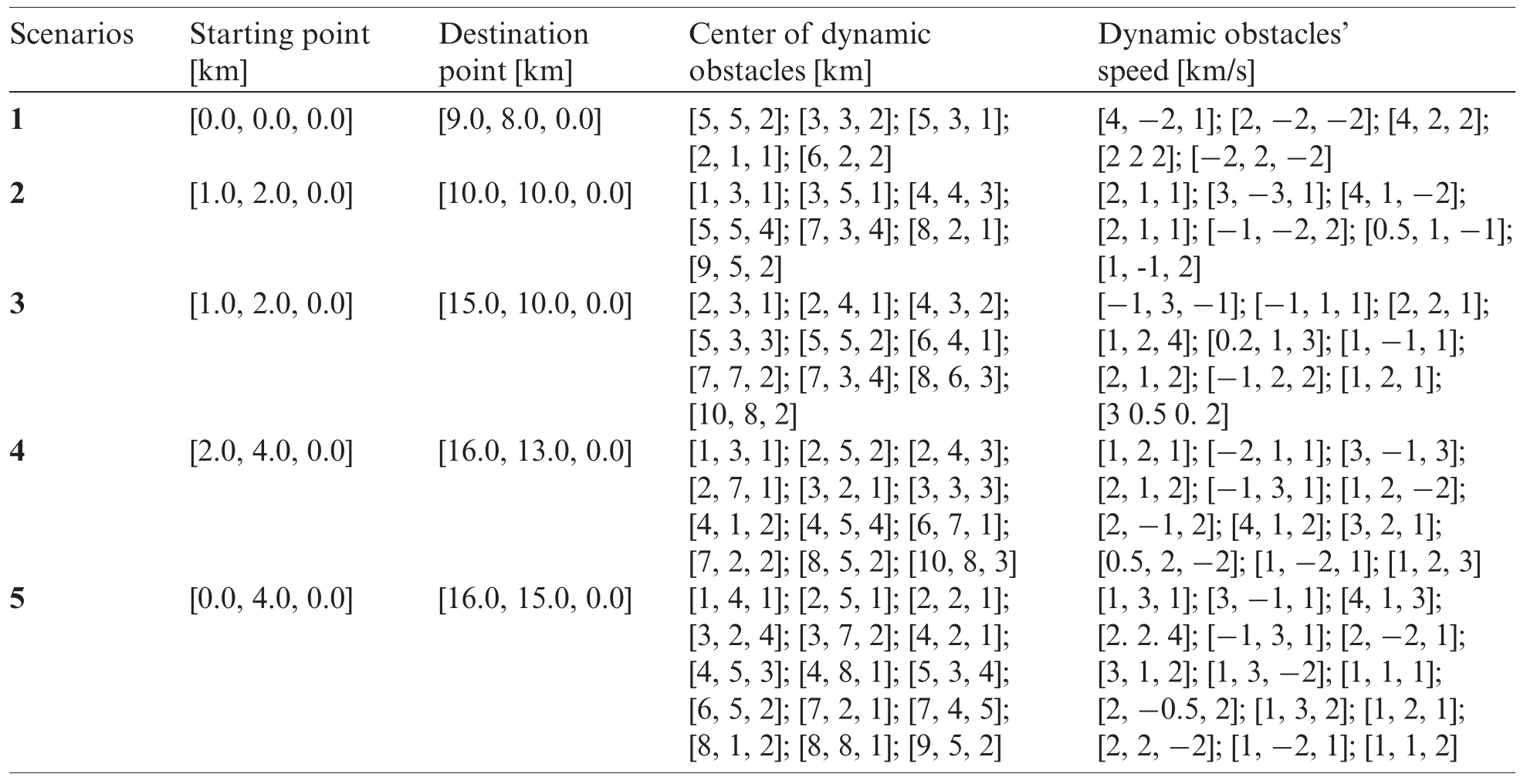
Table 1:Values of the simulation parameters

Table 2:Control parameters of the reported optimizers

These results show the repartition topology of the set of optimal non-dominated Pareto solutions on the compromised surface.A higher-level decision-making approach,i.e.,the modified TOPSIS,selects the best compromise solution.These illustrative results show the high optimization performance of the proposed MOMVO algorithm in terms of convergence dynamics and solution distribution.The optimal Pareto solutions are strongly distributed for the two considered objectives of Eqs.(1) and (2) and under operational constraints of Eq.(13),which means a good coverage of the non-dominated set of solutions of the optimization problem (14) for proposed algorithms,except the NSGAII one which it could only find some feasible solutions.

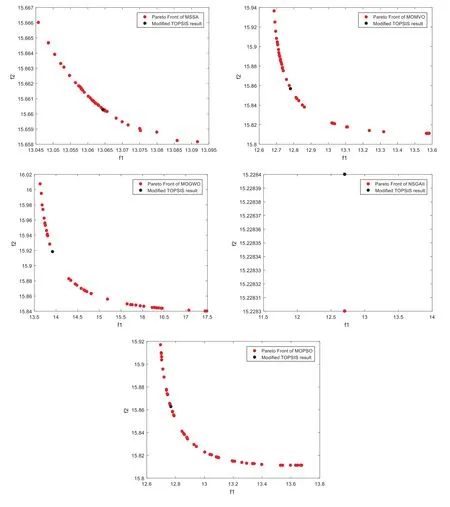
Figure 3:Pareto Fronts for the generation of the first position

To highlight the diversity and coverage of the obtained non-dominated solutions,various metrics such as Maximum Spread (MS) [33,34],Hyper Volume (HV) [35],and C metric [36]have been employed in this study.The statistical results for the MS metric are presented in Tab.3.The proposed MOMVO algorithm is superior to the other reported optimizers in terms of the largest value of MS metric.It becomes the best in terms of having high coverage properties.Tab.4 shows the optimization results of the HV index for the reported algorithms.The statistical results show that the MOGWO algorithm followed by the MOMVO presents the two best solvers compared with other proposed algorithms in terms of diversity and convergence performance.Tab.5 shows the comparative results for the reported algorithms in terms of the C metric.The proposed MOMVO solver surpassed all the other competitive ones and it dominates more than 2% of the MSSA solutions,99% of the MOGWO solutions,15% of the NSGA-II solutions,and 4 % of the MOPSO solutions on average.

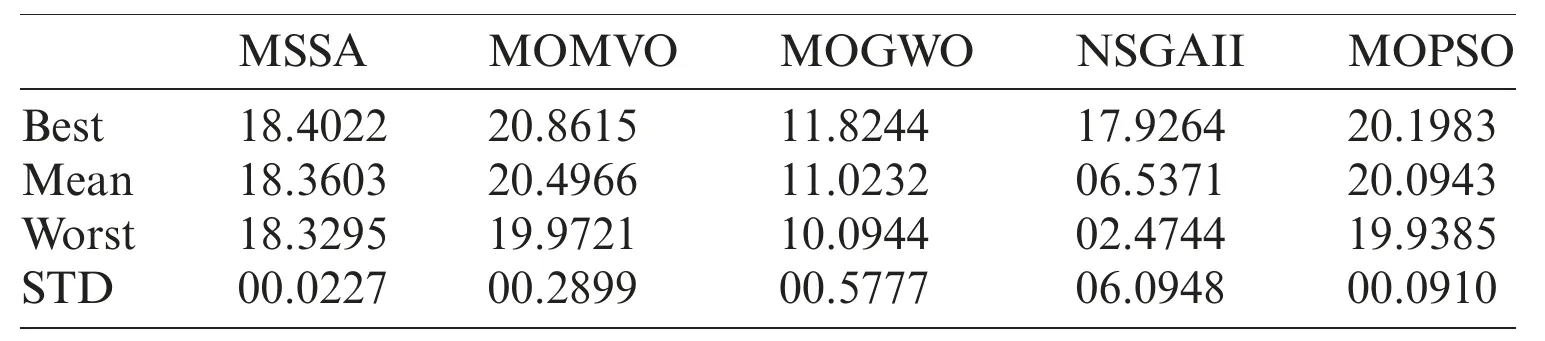
Table 3:Comparison of the MS metric for the reported algorithms

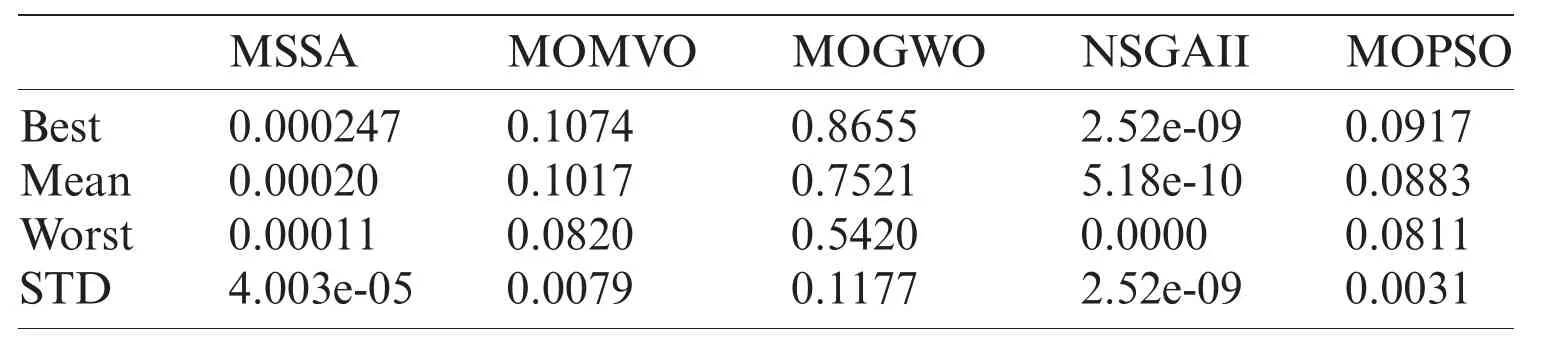
Table 4:Comparison of the HV metric for the reported algorithms

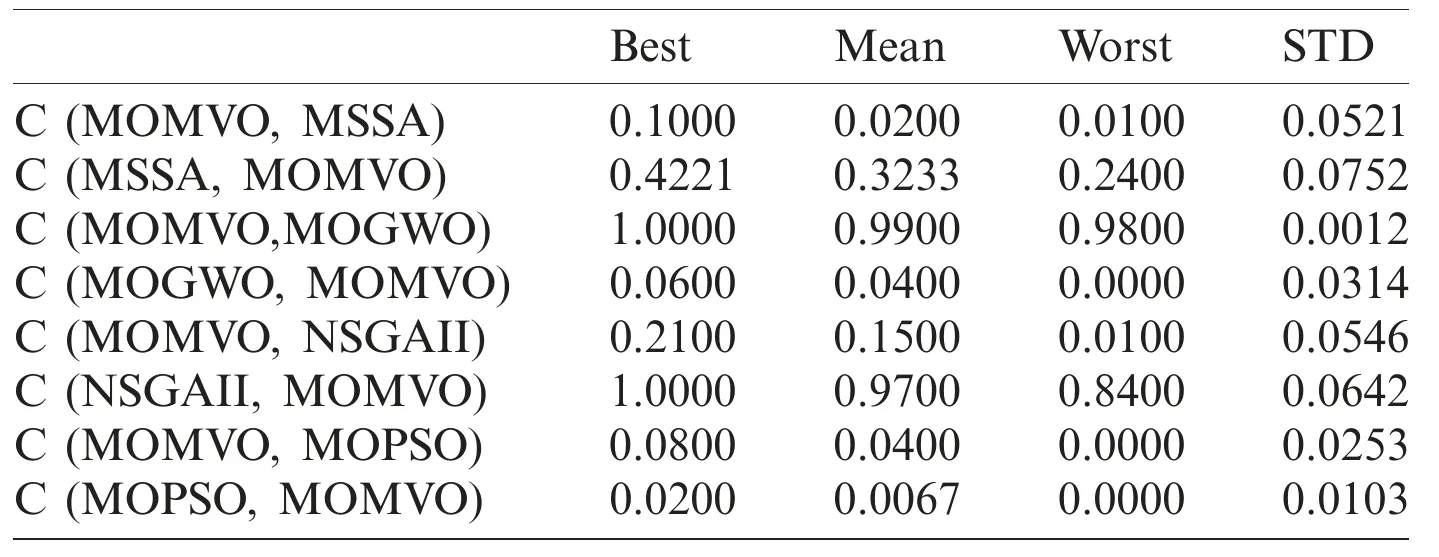
Table 5:Comparison of the C metric for the reported algorithms

To analyze the statistical performance of the MOMVO-based planning method,a comparative study with MSSA,MOGWO,NSGAII,and MOPSO algorithms is performed on three performance criteria,such as path length,elapsed time,and capacity to avoid the moving obstacles as shown in Tab.6.While considering two performance criteria,i.e.,path length and path travel times,a statistical comparison according to its mean value based on the nonparametric Friedman test is implemented and discussed to indicate the significant differences among the performances of the reported algorithms.The Iman-Davenport extension of the classical Friedman test [37]provides the computed valueFF1=27.25 for the elapsed time criterion andFF2=79.33 for the flight time criterion.For the five reported algorithms (ζ=5) and five scenarios (λ=5) at a 95%level of significance,the critical value of theFdistribution withζ-1 and(ζ-1)(λ-1)degrees of freedom is equal toF4,16,0.05=3.01＜FF1＜FF2.So the null hypothesis is declined and there are significant differences among the performance.

Table 6:Optimization result of the path length and the flight time

To find out which algorithms differ from the others,Fisher’s LSD post-hoc test is applied [37].The ranks’sums for all the proposed methods in the different scenarios for the two performance indices are summarized in Tabs.7 and 8.The paired comparisons are given in Tabs.9 and 10.The bold and underlined values indicate that the absolute difference of the rank’s sumis greater than the critical values 4.2398 and 2.5963 for the path length and flight time criteria,respectively [37].From the statistical results based on the two performance criteria,i.e.,path length and path travel time,it is obvious that the MOMVO algorithm outperforms the other reported algorithms for the path planning problem of the quadrotor in the considered dynamic environment.

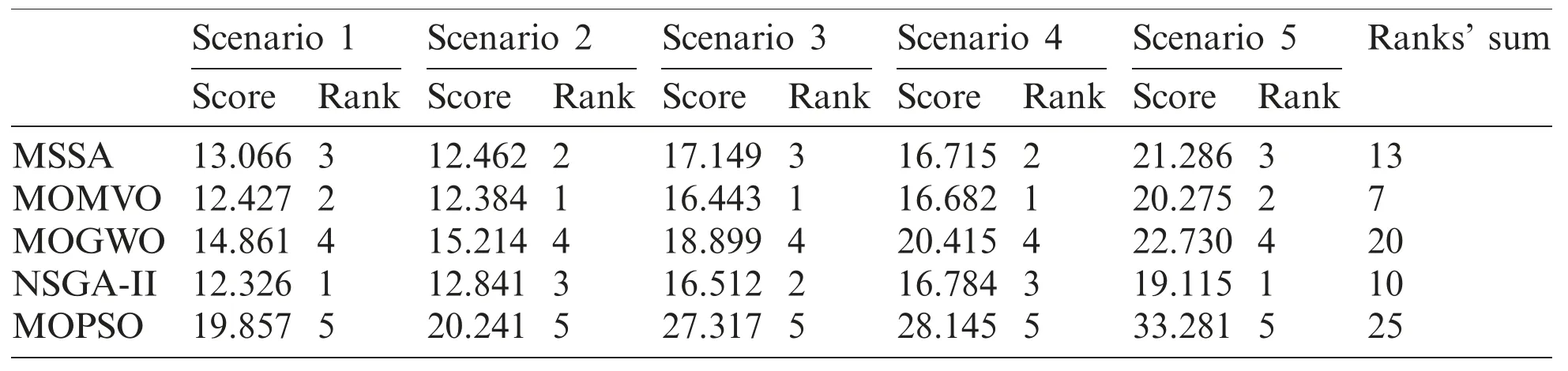
Table 7:Ranks’sum of mean performances:path length criterion

Table 8:Ranks’sum of mean performances:path travel time criterion

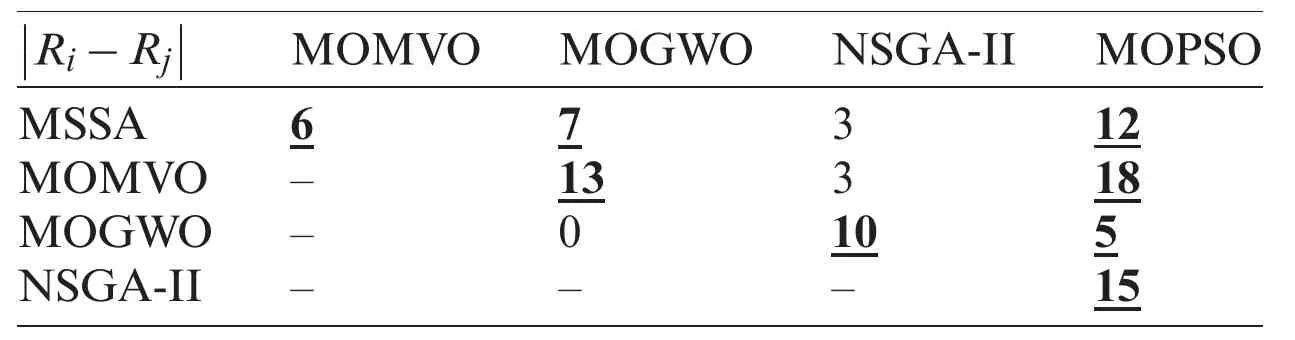
Table 9:Paired comparison of the proposed metaheuristics:path length criterion

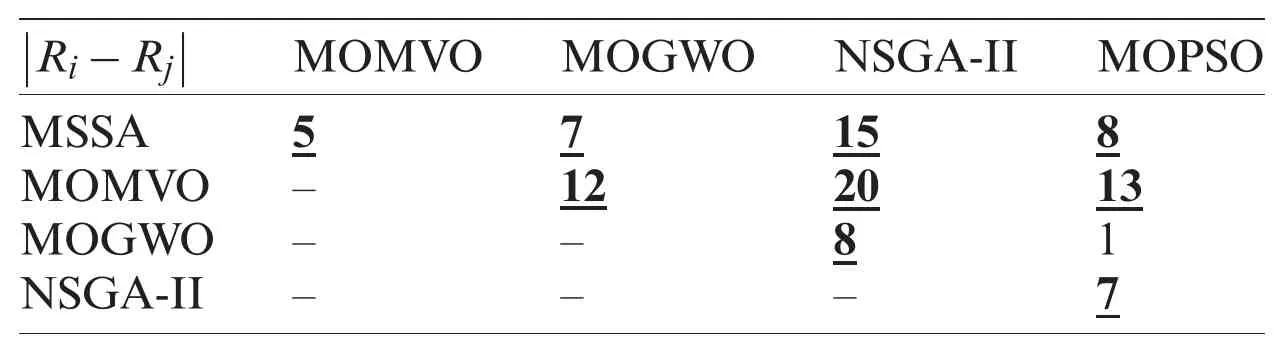
Table 10:Paired comparison of the proposed metaheuristics:path travel time criterion

By visualizing the simulations of the 3D trajectory of the quadrotor,all proposed algorithms succeed in completing the flight mission still avoiding all the moving obstacles.The simulation results of the proposed MOMVO-based method are shown in Fig.4.Several periods of time are given where T is the total time of the UAV path planning.These results show that the quadrotor avoids all dynamic obstacles in all four periods of time and guarantee the planning performance of the proposed MOMVO-based method.The time-domain responses of the controlled position dynamics are shown in Figs.5-9 corresponding to the mean case of the multicriteria optimization.The proposed flight PID controllers allow the quadrotor to reach the desired trajectories.The PID controller gains’selection is achieved by an iterative trials-errors-based method.Even though there were minor tracking errors in the time-domain responses of the closed-loop,these results remain encouraging.The tracking errors can be due to using PID gains that were not defined from the control design approach but by trials-errors based tuning.

By visualizing these figures,we can notice that the proposed algorithm MOMVO gives the most direct path,which guarantees high efficiency in flight missions.The MOPSO algorithm generates a trajectory with many fluctuations along the Z-axis.From these results,the quadrotor has started the mission after a time delay which is due to the calculation time of the next point.A minimum execution time for an algorithm ensures the high efficiency of collision avoidance with the dynamic obstacles and causes a minimum flight time.

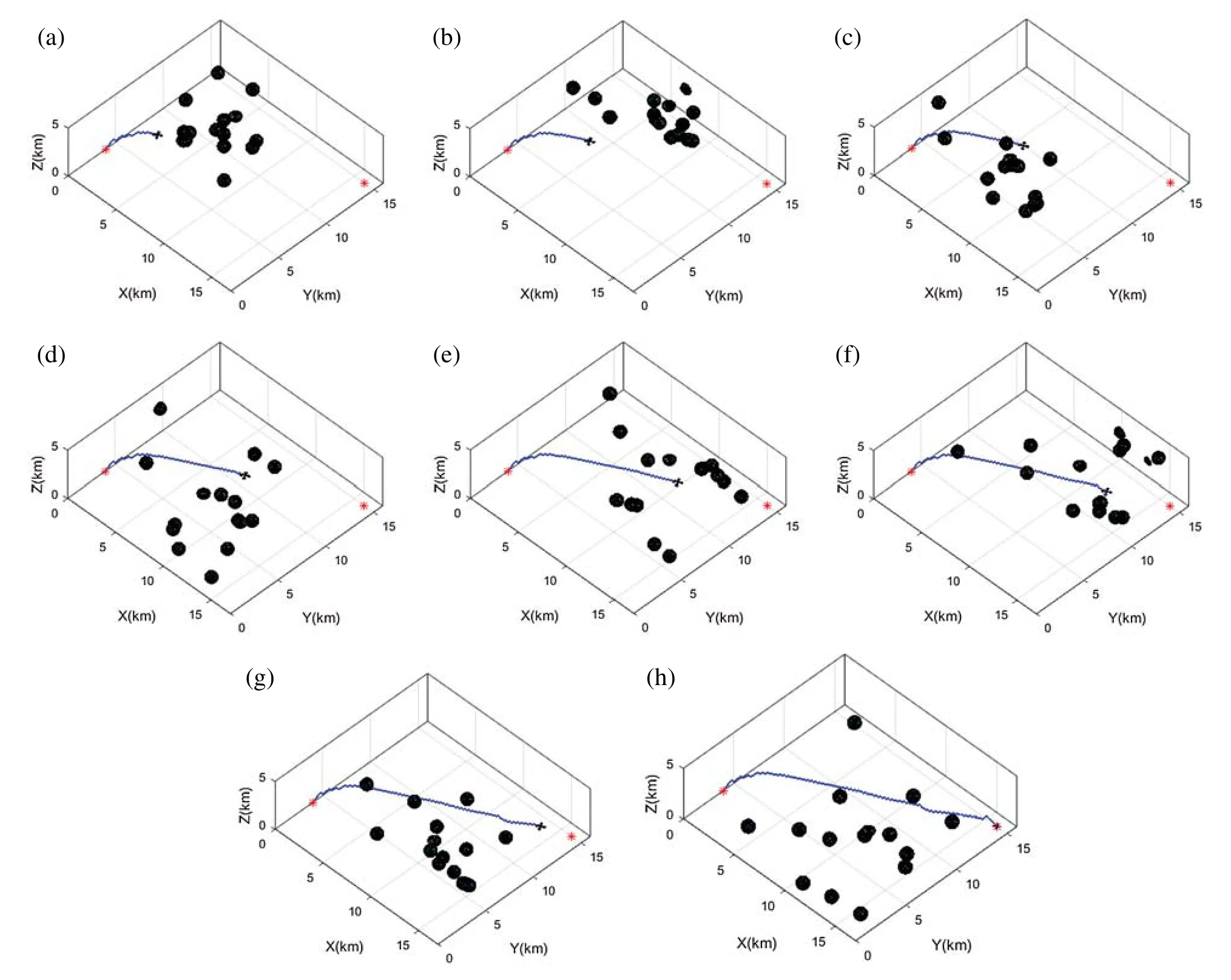
Figure 4:Planned path tracking in scenario 5 for the proposed MOMVO-based approach:(a) T/8;(b) 2T/8;(c) 3T/8;(d) 4T/8;(e) 5T/8;(f) 6T/8;(g) 7T/8;(h) total mission time (T)

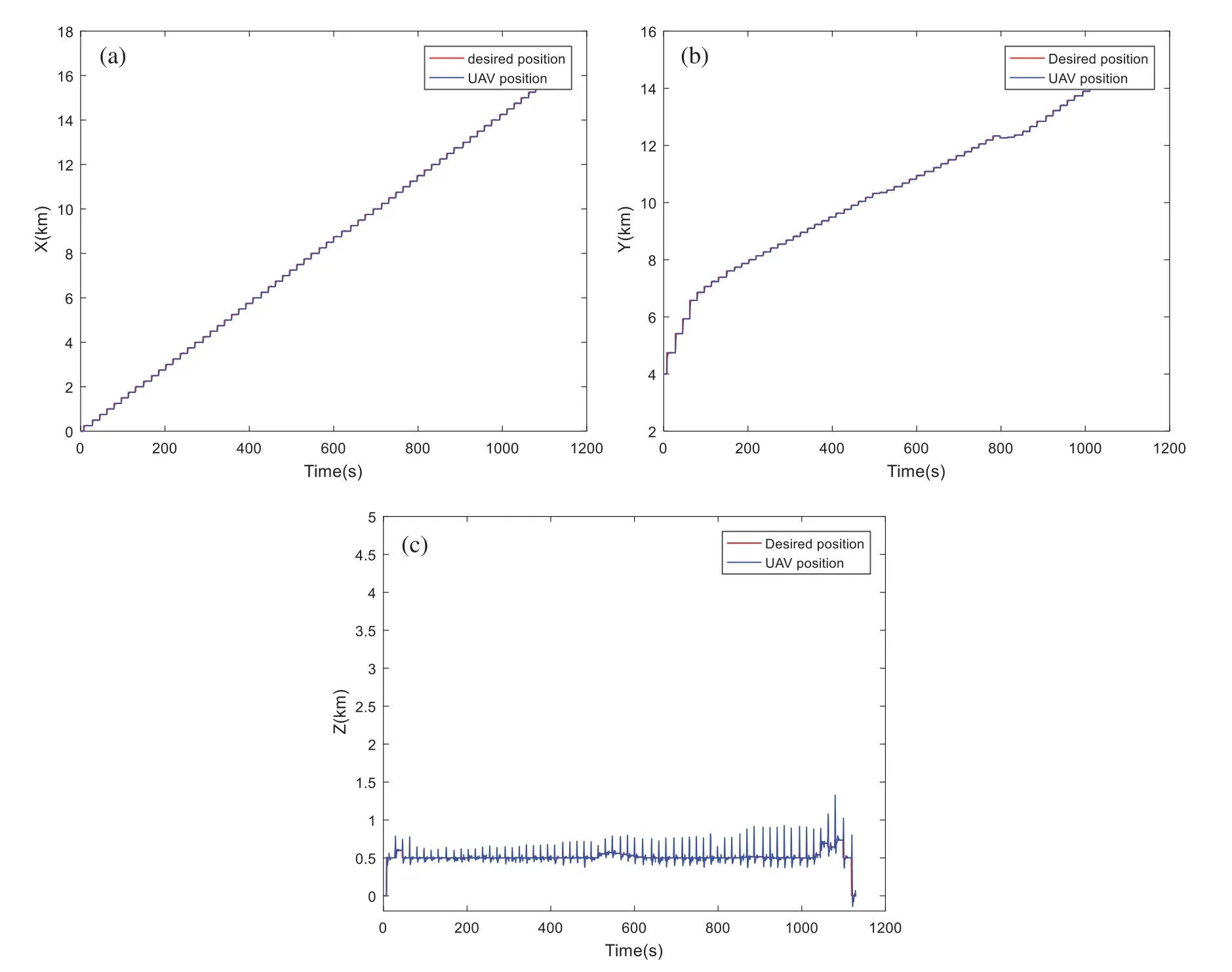
Figure 5:Position tracking based on MOMVO algorithm:(a) Tracking dynamics on X-axis;(b) Tracking dynamics on Y-axis;(c) Tracking dynamics on Z-axis

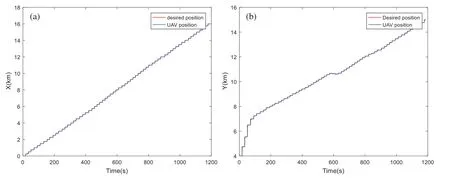
Figure 6:Position tracking based on MSSA algorithm:(a) Tracking dynamics on X-axis;(b) Tracking dynamics on Y-axis;(c) Tracking dynamics on Z-axis

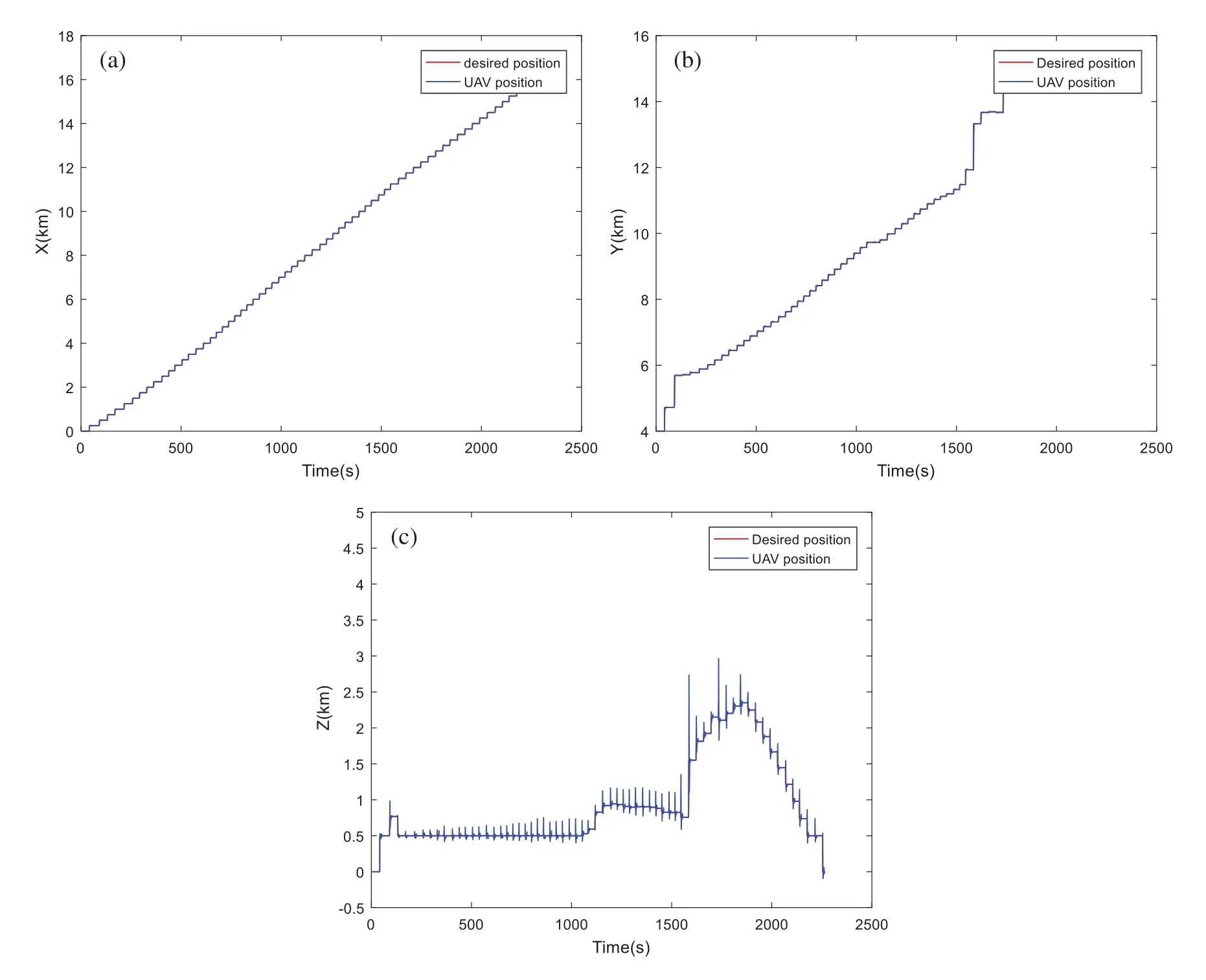
Figure 7:Position tracking based on MOGWO algorithm:(a) Tracking dynamics on X-axis;(b) Tracking dynamics on Y-axis;(c) Tracking dynamics on Z-axis

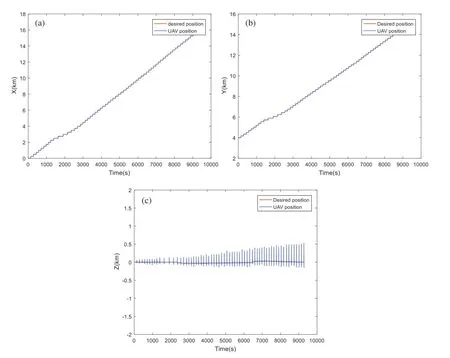
Figure 8:Position tracking based on NSGA-II algorithm:(a) Tracking dynamics on X-axis;(b) Tracking dynamics on Y-axis;(c) Tracking dynamics on Z-axis

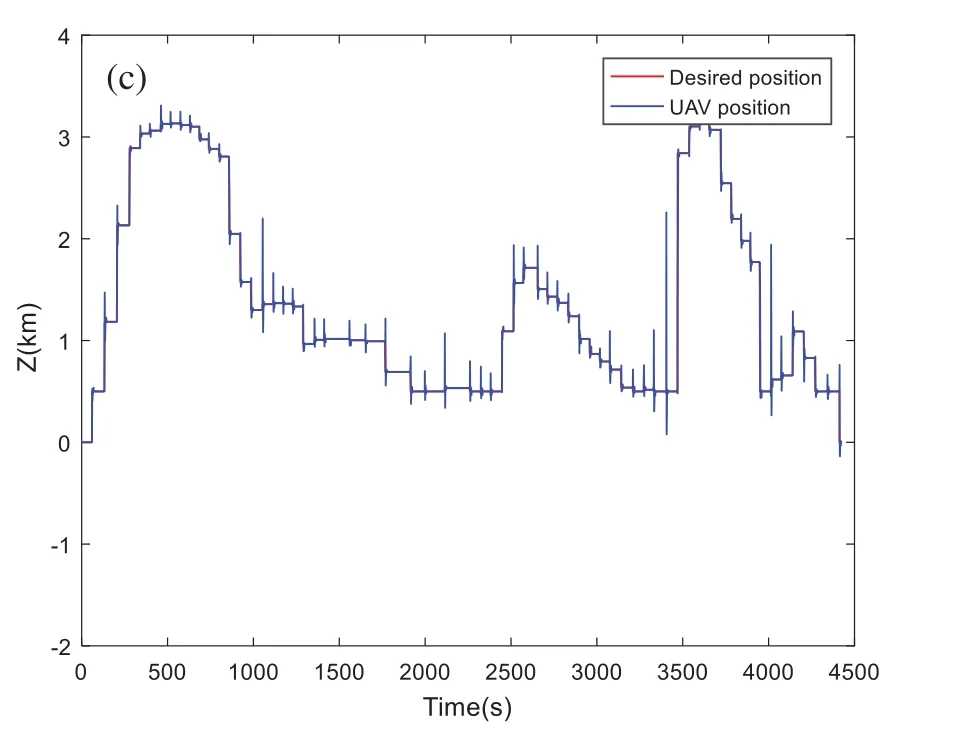
Figure 9:Position tracking based on MOPSO algorithm:(a) Tracking dynamics on X-axis;(b) Tracking dynamics on Y-axis;(c) Tracking dynamics on Z-axis

6 Conclusions

In this paper,a multi-objective multi-verse optimizer-based method has been proposed and successfully applied to solve the path planning problem of quadrotors UAV in a 3D dynamic environment.The path planning problem was formulated as a multi-objective optimization problem under operational constraints.The proposed planning approach aims to lead the drone to traverse a short and fast path in a dynamic environment without collision with the moving obstacles.An interactive graphical interface was developed under MATLAB/Simulink software environment to implement the proposed MOMVO-based path planning strategy.The demonstrative results and nonparametric statistical analyses in the sense of Friedman and the post-hoc tests show that the proposed MOMVO-based method is efficient and powerful compared to other reported algorithms.In comparison with MSSA,MOGWO,MOPSO,and NSGA-II optimizers,the main advantages of the proposed multi-verse algorithm are the remarkable simplicity of software implementation as well as the reduced number of its control parameters.The exploration/exploitation capabilities are superior to those of the other reported algorithms.Besides,the paired comparisons for two different optimization criteria showed that the MOMVO algorithm outperforms all the reported optimizers.

Future works deal with the real-world prototyping and experimentation of the proposed MOMVO-based planning approach using a real model of quadrotor available in our laboratory.The Parrot AR.Drone 2.0 kit associated with MATLAB/Simulink software will be used for the experimentations.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.

Appendix A:Quadrotor’s model parameters

Symbol Description Value/unit b Lift coefficient 2.984×10-5 N.s2/rad2 d Drag coefficient 3.30×10-7 N.s2/rad2 mQ Mass 0.5 Kg l Arm length 0.50 m Jr Motor inertia 2.8385×10-5 Kg m2 Ix,Iy,Iz Quadrotor inertia 0.005,0.005,0.010 κ1,2,3 Aerodynamic friction coefficients 0.3729 κ4,5,6 Translational drag coefficients 5.56×10-4 g Acceleration of the gravity 9.81 m.s-2