分析约束的集合预报初始扰动构造方案的研究

潘贤 王秋萍 张瑜 何佩仪 马旭林

1 南京信息工程大学气象灾害教育部重点实验室，南京 201144

2 河南省气象探测数据中心，郑州 450003

3 中国民航西南地区空中交通管理局气象中心，成都 610202

1 引言

数值天气预报的初始误差和模式误差等限制了非线性大气运动的单一确定性预报技巧（Lorenz,1963, 1969; Epstein, 1969; Leith, 1974），而集合预报通过旨在合理表征上述两类主要误差导致的预报不确定性，进而给出未来大气运动演变的概率密度函数以解决单一数值解的缺陷，在极端天气的辨识度、预报可信度等方面具有显著优势（杜钧和陈静, 2010; 杜钧和邓国, 2010; 李晓莉等, 2019; 陈静和李晓莉, 2020）。集合预报质量很大程度上取决于集合初始扰动对大气运动不确定性描述的准确程度。合理的集合预报扰动能够捕获初始场和预报场中快速增长的误差，合理表征其预报不确定性。因此，集合扰动结构及演变特征和预报误差结构与传播规律的一致性对提高集合预报质量至关重要（马旭林等, 2014; Keresturi et al., 2019）。

经典的蒙特卡洛初始扰动构造方案假定真实大气中的初始误差满足随机分布规律，其初始扰动虽然可以描述大气的不确定性特征，但由于缺乏动力增长的物理机制，难以反映预报误差的流依赖特征，导致预报集合成员之间的离散度通常偏小（马旭林等, 2018）。时间滞后平均法（Lagged Average Forecasting, LAF; Hoffman and Kalnay, 1983）由于引入了实际预报误差，其扰动质量通常优于蒙特卡洛随机扰动法。但是由于受到预报时效的限制，构造的集合成员数有限。多年来，针对集合预报初始扰动构造方案的研究不断取得新的进展（陈浩等,2017），如具有动力约束且较好反映大气斜压性的增长模繁殖法（Breeding of Growing Modes , BGM;Toth and Kalnay, 1993, 1997）与能够快速识别预报误差增长模态的奇异向量法（Singular Vectors,SVs; Buizza and Palmer, 1995; Molteni et al., 1996;Walser et al., 2006; 李晓莉和刘永柱, 2019）等。这两种方法构造的集合初始扰动具有大气动力学结构，在模式预报中通常能够较合理增长，但难以有效描述中小尺度天气系统预报误差的发展和演变特征。近年来发展的集合预报扰动方案综合考虑了集合扰动和观测资料不确定性，如集合变换（Ensemble Transform, ET; Wei et al., 2006, 2008）、尺度化集合变换（ Ensemble Transform with Rescaling,ETR; Bishop and Toth, 1999）与集合变换卡尔曼滤波（Ensemble Transform Kalman Filter, ETKF; Wang and Bishop, 2003; 马旭林等, 2008; Szunyogh et al.,2008; Bowler and Mylne, 2009）等方法。其中，ETKF方法利用变换矩阵将预报扰动转化为与卡尔曼滤波误差协方差更新方程一致的分析扰动，保证了初始扰动在标准化观测空间具有正交性，并能够吸收观测精度与密度的空间分布的观测信息。

随着集合扰动和资料同化的深入研究和理解，集合初始扰动方案与集合同化紧密结合协同发展。欧洲中期天气预报中心（ECMWF）从2010 年起采用的奇异向量（SVs）和集合资料同化（Ensemble Data Assimilation, EDA）相结合的初始扰动方法，使得SVs 与EDA 优势互补，获得了技巧性更高的概率预报（Buizza et al., 2008, 2010），但该方法需要巨大计算资源；美国国家环境预报中心（NCEP）则将其原集合初始扰动构造方案与其全球资料同化系统相结合而形成了集合卡尔曼滤波方案（Ensemble Kalman Filter, EnKF; Wang et al.,2019），并逐渐拓展到区域集合预报并取得了一定的应用效果（刘永柱等, 2013）。由于上述初始扰动方案中包含的大尺度扰动信息质量偏低，若直接将其用于区域集合预报，通常会影响集合离散度的合理发展（Caron, 2013; 张涵斌等, 2017），从而提出了动力降尺度方法。受到当前模式水平分辨率的制约，降尺度的集合扰动包含的小尺度扰动信息并不充分。陈静等（2005）针对中尺度暴雨集合预报提出的异物理模态初值扰动方案表现出了较好的中尺度特征。尺度混合初始扰动方案（Chen et al.,2008; Wang et al., 2014）将较高质量全球预报场的大尺度信息和包含丰富中小尺度信息的区域预报场合理耦合，较好地解决了大尺度和中小尺度不确定性信息，对大尺度强迫较强或者偏弱（强对流性）的天气系统均具有较好的适用性（马旭林等,2018）。Zhang et al.（2015）对T639 全球集合预报降尺度扰动和ETKF 扰动进行多尺度混合扰动试验表明其预报技巧得到了改进。马旭林等（2018）将T639 全球模式预报中高质量的大尺度信息与GRAPES 区域预报中丰富的中小尺度信息有效融合，进一步验证了该方案具备较好改善区域集合预报质量的能力。

集合初始扰动只有合理描述实际大气运动状态变化的预报误差结构和大小，其在预报过程中的发展和演变才能够更准确地表征预报误差的特点。现有集合初始扰动方案更多的考虑了模式预报误差的结构和分布特点，能够较合理地描述大尺度扰动信息，但仍难以合理描述中小尺度预报误差的不确定性，特别是局地性中小尺度天气系统的集合扰动，而且通常包含有虚假扰动信息，导致存在离散度不够合理，集合辨识度和可靠性偏低等诸多不足（王婧卓等, 2018; 张瑜, 2019）。当前，随着集合预报与资料同化的研究不断深入，将二者紧密联系相互促进成为了集合预报与资料同化发展的趋势（马旭林等, 2014）。本文在对不同天气尺度集合扰动的物理结构及其在预报中增长和演变特征研究的基础上（马旭林等, 2021），考虑不同空间尺度天气系统预报误差的物理结构与资料同化分析误差的一致性信息，研究可有效表征观测和预报不确定性的资料同化分析增量对集合初始扰动物理约束的有效性，探索利用分析增量对初始扰动中不合理的集合扰动信息进行物理约束的科学方案，以提高集合初始扰动的物理结构和振幅与预报误差的一致性，改善集合初始扰动质量，从而提高集合预报的综合性能。

2 分析约束方法与试验方案

通常情况下，理想的集合初始扰动能够合理反映模式初始场的不确定性，即其扰动结构与主要天气系统相吻合，扰动振幅与其预报误差相当。而不尽合理的集合初始扰动的物理结构通常偏离主要天气影响系统，其扰动振幅与预报误差也存在不同程度的差异。事实上，由于大气运动状态变化和天气系统多尺度相互作用的复杂性以及初始扰动方案的不完美性等原因，当前仅依靠初始扰动方案仍难以构造出完全合理的集合扰动，特别对中小尺度天气系统而言。将集合初始扰动的构造与资料同化的分析信息相结合应是一种合理的选择。

2.1 分析约束方法

资料同化的分析增量同时包含有观测不确定性和预报（背景场）不确定性信息。借助集合预报中控制预报的同化分析增量信息，通过构造分析约束函数，对集合初始扰动进行合理调整，改善其物理结构和扰动振幅，使其能够更加合理的表征实际大气的预报不确定性，增强集合初始扰动与初始误差的一致性，此即分析约束。该分析约束扰动方案以现有集合扰动为基础，既可以充分吸收高质量的资料同化分析场的有效信息以改善集合扰动质量，又不显著增加集合系统所需要的计算资源。其分析约束效果与集合预报扰动成员数无关，仅受控制预报分析质量的影响。

分析约束初始扰动方案利用资料同化中新息向量与观测误差的质量控制经验关系，将原集合初始扰动与分析增量相比较，识别出异常不合理的集合初始扰动，依据引入适当的分析增量信息对不尽合理的初始扰动进行分析约束，使得约束后的集合扰动的结构与振幅尽可能与不同尺度天气系统的初始误差相一致，而对于相对合理的集合初始扰动则予以保留。该方案具有合理的物理基础，相对于EDA 方案（Buizza et al., 2008, 2010），计算量小、容易实现，且具备改善集合扰动质量的理论依据。其具体方案如下：

其中，w为分析约束函数。为了对照试验结果，首先将分析约束函数设置为简化的常值函数，记为w1，即

基于资料同化系统中观测值与其初估值之差（即新息向量）的绝对值大于三倍观测误差即剔除该观测资料的质量控制标准，这里将3 倍分析增量作为判断集合扰动是否合理的临界阈值，即当集合扰动的振幅小于等于3 倍的分析增量时，认为该扰动属于合理范围，对原集合扰动不做任何调整；当扰动的振幅大于3 倍的分析增量时，认为该扰动包含有虚假扰动信息，则基于分析增量通过分析约束函数调整集合扰动，剔除虚假扰动信息。

在简化的分析约束函数w1方案的基础上，基于标准正态分布函数特征，构建一个能够随集合扰动合理性程度自适应调整的分析约束函数w2，基于分析增量对不合理的集合扰动信息实现自动调整，其数学表达式为

其中， μ表示各高度层上所有格点扰动与分析增量差值绝对值的平均，σ2表示相应的方差。从式（3）可以看出，当扰动振辐大于3 倍分析增量时，随着集合扰动与分析增量之间差异的增大，w2会不断趋近于零，即当扰动的不合理程度越强，更新后的扰动中原扰动所占比例越小，分析增量所占比例越大。基于上述分析约束方案，对风场、质量场和湿度场等基本物理量场原集合初始扰动的结构和振幅进行约束调整。

2.2 资料与试验方案

分析约束前的集合初始扰动源于ETKF 初始扰动方案构造的GRAPES 区域集合预报，水平分辨率为0.1°×0.1°，垂直方向分为31 层，模拟区域为（16.5°N～58.35°N，71.5°E～133.6°E），包含1个控制预报和14 个扰动预报的15 个集合成员。T639 全球集合预报源于中国气象局数值预报中心的全球业务集合预报，水平分辨率为0.28125°×0.28125°，每6 h 更新一次，其初始扰动方案为增长模繁殖法。降水观测资料为中国自动站与CMORPH 降水产品融合的逐小时降水量数据，水平分辨率为0.1°×0.1°。

试验以2015 年7 月14～17 日的一次降水过程进行个例对比分析。此次过程主要受高空槽、低层切变、低涡等天气系统的影响，前期降水主要落区位于四川中南部、重庆大部、贵州西北部以及湖北与河南交界处。预报起始时间为2015 年7 月14日00 时（世界协调时，下同），每6 h 输出一次预报结果，预报时效为72 h。基于分析约束扰动方案，即公式（1），利用不同的分析约束函数公式（2）和公式（3），构成三组集合初始扰动进行区域集合预报，可得到三组对比试验结果。三组试验的集合初始扰动分别为（1）T639 降尺度12 h 预报场的集合扰动（REPS 试验）；（2）分析约束函数w1（Cons_w1试验）和（3）分析约束函数w2（Cons-w2试验）分别进行分析约束后构成的集合扰动。将上述三组试验获得的集合初始扰动构成集合成员的模式初值开展区域集合预报，分别得到三组预报结果。

3 分析约束对初始扰动的影响

3.1 分析增量的空间分布特征

合理的分析增量空间分布是构建分析约束的集合扰动的基础。图1 是单个集合成员850 hPa 位势高度、温度和风场的分析增量，其中等值线表示的位势高度和风矢源于控制预报（如非特殊说明，下文图中均与此相同）。从天气形势上来看，对流层低层的西北风和西南风的切变线贯穿陕西中部和南部并且一直延伸至四川中部。高度场的分析增量与低层切变及其后方的低压吻合较好，纬向风和经向风的分析增量振幅较小，分布基本合理；尽管高原北部温度场的分析增量出现一个可能受地形影响导致的较大负值中心，总体上与低层天气系统依然存在一定的对应关系。对流层中层（500 hPa）分析增量的大值区与主要天气系统快速发展的区域也基本一致（图略）。综合来看，在对流层低层和中层，分析增量与天气形势基本吻合，反映了分析增量分布合理性，这是分析约束扰动方案的基础。

图1 2015 年7 月14 日00 时（协调世界时，下同）控制预报的850 hPa 风场（风矢）、位势高度（等值线，单位：gpm）和（a）位势高度、（b）温度、（c）纬向风和（d）经向风分析增量（彩色阴影）。灰色阴影为地形（下同）Fig. 1 The 850-hPa wind field (wind vector), geopotential height (contour, units; gpm) of the control forecast, and the analysis increments of(a) geopotential height, (b) temperature, (c) zonal wind, (d) meridional wind at 0000 UTC on 14 July 2015. Gray shadows are terrain (the same below)

3.2 集合初始扰动与分析增量的差异

分析增量表征观测对背景场的调整程度，也反映预报场（背景场）与观测的不一致性。从850 hPa不同物理量的集合初始扰动与分析增量的差异（图2）可以看出，对流层低层二者的纬向风和经向风的比值存在异常大或小值区，呈现纬向（图2a）和经向（图2b）条带状分布，且异常区多位于系统快速发展之处，如低涡系统或切变线附近以及东南沿海以及台风附近等。如果认为分析增量相对准确，则这些条带状的比值异常区的扰动存在显著的不合理。

高度（图2c）和温度（图2d）集合初始扰动与分析增量差值的分布更直观地展现了二者的差异。高度场差值的大值区主要集中于40°N 以南，且正值为主，即集合扰动相对分析增量异常偏大（图2c）；温度扰动的量值在高原北部以及（45°N，106°E）附近的低压周围显著偏大，而在低压东部部分区域温度扰动相对偏小（图2d）。500 hPa 上二者的差异与此类似（图略），这也更直观地反映出了原集合初始扰动的不合理性。

图2 2015 年7 月14 日00 时 850 hPa 单个集合成员的初始扰动与分析增量的比值：（a）纬向风；（b）经向风。2015 年7 月14 日00 时850 hPa 单个集合成员的初始扰动与分析增量的差值：（c）高度；（d）温度。等值线为控制预报的位势高度（单位：gpm），灰色阴影为地形Fig. 2 Ratios between the initial perturbations of an ensemble member and analysis increments on the 850-hPa wind field at 0000 UTC on 14 July 2015: (a) Zonal wind and (b) meridional wind ratios; differences between the initial perturbations of an ensemble member and analysis increments on the 850-hPa wind field at 0000 UTC on 14 July 2015 (c) height and (d) temperature deviations. The contour lines indicate geopotential height (units:gpm), the gray shadows indicate terrain

3.3 分析约束前后初始扰动对比分析

集合初始扰动的不合理程度直接影响集合预报的性能。采用分析约束对其不合理之处进行适当调整，以增加初始扰动表征预报误差结构的能力。分别基于公式（2）w1和公式（3）w2的分析约束函数构造集合初始扰动的分析约束方案，从同化分析场提取出分析增量，对区域集合预报扰动进行调整，得到分析约束的集合初始扰动，并对分析约束前后扰动的水平分布特征进行比较。

3.3.1 对流层低层扰动的分析约束效果

对比约束前后850 hPa 经向风扰动（图3）可以发现，以w1、w2的约束函数分析约束后，低层切变线附近的中小尺度扰动信息被较好地保留，仅是振幅上略微减弱，而位于（45°N，106°E）的浅低压系统，其周围的原初始扰动偏大而不够合理。以方案w1分析约束后，扰动的基本结构与原本相似，扰动振幅则明显减弱，使得低压周围的扰动结构有所改善（图3b）；而以方案w2分析约束后，该区域的扰动不论是在分布结构还是振幅都得到明显调整，更加趋于合理（图3c）。同时，注意到（28°N～35°N，125°E～133°E）附近等压线分布较为稀疏，原扰动在该区域异常偏大，明显存在虚假扰动信息，而以w1分析约束后，该区域显著偏大的初始扰动明显减小；以w2分析约束后，该区域初始扰动振幅得到减小调整，其结构与天气系统的一致性也更加趋于合理。分析约束前后纬向风与质量场的调整与此类似（图略）。

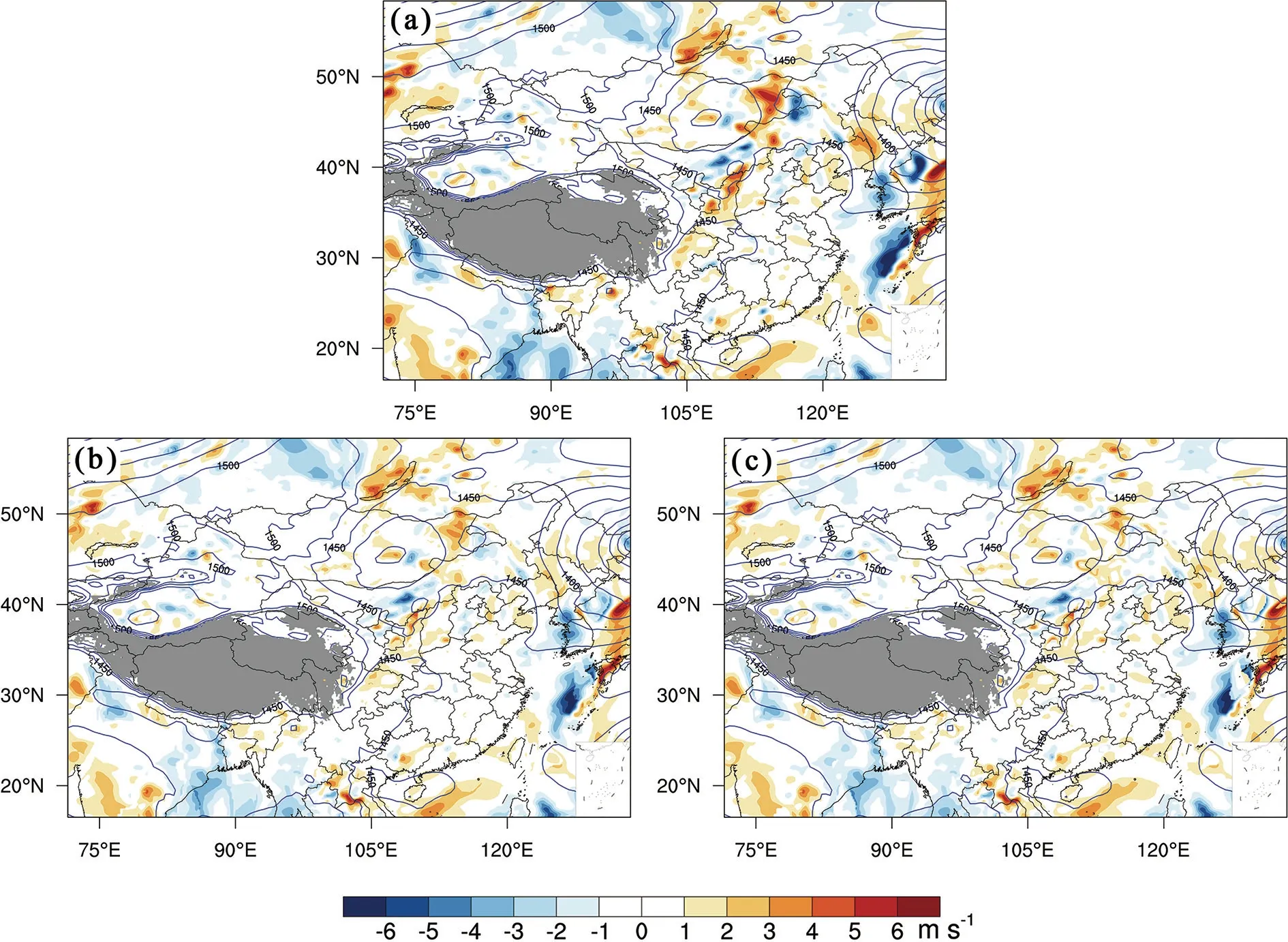
图3 （a）分析约束前与分析约束（b）Cons-w1 试验、（c）Cons-w2 试验的850 hPa 经向风场初始扰动（等值线为位势高度，单位：gpm）Fig. 3 Initial perturbation of the 850-hPa meridional wind field (the contour lines indicate geopotential height, units: gpm) (a) without analysis constraint and Expts (b) Cons-w1 and (c) Cons-w2 with analysis constraint

3.3.2 分析约束对对流层中层的影响

图4 为对流层中层位势高度场的初始扰动（图4a）和分析约束函数w1（图4b）、分析约束函数w2（图4c）调整后的扰动。对比发现，经过约束函数w1约束后，500 hPa 的蒙古冷涡中心以及其西北侧脊区的位势高度虚假扰动明显减小，同时还保留了中低纬度地区的小扰动信息。但是，冷涡东侧的深厚低压附近的扰动也被大大削弱，而考虑到该地区的天气形势及其等压线疏密程度，低压外围应存在合理的扰动（图4b）。从w2分析约束后的结果来看，蒙古冷涡中心以及其西北侧脊区的扰动减弱效果相较w1更加明显，且对冷涡东侧低压外围的扰动调整得更加合理（图4c）。对流层中层其他质量场和风场的初始扰动在分析约束前后也表现出较好的调整效果。

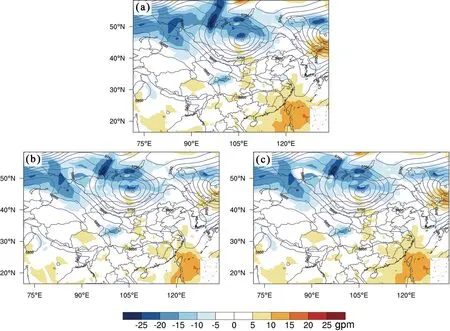
图4 （a）分析约束前与分析约束（b）Cons-w1、（c）Cons-w2 的500 hPa 位势高度场初始扰动（等值线为位势高度，单位：gpm）Fig. 4 Initial perturbation of the 500-hPa height field (the contour lines indicate geopotential height, units: gpm) (a) without analysis constraint and Expts (b) Cons-w1 and (c) Cons-w2 with analysis constraint

综合来看，两种分析约束方案均对原扰动中不合理的扰动均可有效进行不同程度的调整，使得约束后的扰动更加趋于合理，从而与天气形势吻合得更好，其中分析约束方案w2对初始扰动的调整更加显著，其约束效果明显优于约束方案w1。

4 分析约束扰动的集合预报效果

前述分析初步表明，对初始扰动中不合理的扰动结构和振幅进行分析约束，能够改善集合初始扰动质量，但这种相对合理的初始扰动对集合预报质量的贡献尚需要进一步验证。试验分为三组：首先，将原初始扰动与控制预报叠加构造集合预报成员的模式初始场；其次，将分析约束函数w1分析约束的初始扰动与控制预报叠加得到第二组集合预报的模式初始场（Cons-w1）；第三，采用分析约束函数w2约束的初始扰动与控制预报构建第三组集合预报模式初始场（Cons-w2）。三组集合预报试验的起报时间均为2015 年7 月14 日00 时，预报时效为72 h。为了更全面客观地评价分析约束扰动前后区域集合预报的效果，同时与相应起报时间和预报时效的T639 全球集合预报（T639），分别从集合预报扰动随预报时间的演变、集合扰动离散度、集合扰动能量等角度对预报结果进行综合分析。

4.1 集合预报扰动的结构与演变

4.1.1 预报扰动的水平演变特征

图5 为2015 年7 月14 日初始时刻00 时（左列）和24 h 预报（右列）的REPS（图5a）和分析约束Cons-w1（图5b）、Cons-w2（图5c）的经向风扰动水平分布特征。REPS 集合初始扰动的异常大值区主要位于贝加尔湖南侧低涡以及河套西部的低槽地区，尤其冷涡西北侧脊区附近的经向风扰动振幅呈现出明显的局地性偏大，存在显著的虚假扰动信息（图5a1）。经分析约束方案Cons-w1（图5b1）和Cons-w2（图5c1）对原REPS 的初始扰动约束后，该区域的虚假扰动具有不同程度的减弱，特别Cons-w2的调整效果更为明显，其中小尺度扰动振幅明显减小。同时，约束调整后依然保留了原初始扰动的中小尺度扰动结构信息。

预报24 h 后，贝加尔湖南侧快速发展的深厚低涡受其东侧低压系统的阻挡，其中心位置基本稳定，南侧低槽东移与南支槽汇合。相应地，槽区的初始扰动也不断东移增强发展，随着东部低压系统的发展，其周围的经向风扰动也逐渐增强。由于该区域的控制预报经向风发展偏弱，故以正扰动为主，其周围的中小尺度扰动也有所发展（图5a2），但集合预报扰动随天气形势变化的特点不完全合理。相比于REPS，两种分析约束方案Cons-w1和Consw2对初始扰动进行约束调整后，虽然初始扰动的振幅明显减小，其扰动结构也不同程度的调整，但经过24 h 预报时间后，中小尺度扰动与天气形势更加吻合，扰动增长并没有变小。这说明，经分析约束调整后，相对REPS 而言，初始扰动的物理结构和振幅与初始误差一致性更高，随天气形势变化而发展演变的规律也更加合理，尤其是Cons-w2约束方案（图5b2 与图5c2）。这是因为分析约束对原初始扰动中的虚假成分进行了有效调整，使得约束后的初始扰动的物理结构和扰动振幅更加合理，而更加合理的扰动在进入预报模式后得到了快速增长。这一方面反映了原REPS 经向风初始扰动中包含有不合理的虚假扰动信息，也进一步说明分析约束扰动方案的调整能够更加有效的捕获到快速增长的中小尺度扰动。分析约束方案对对流层中层纬向风也具有类似的良好调整效果（图略）。

图5 500 hPa 经向风初始扰动（左列）与24 h 预报扰动（右列）的水平分布：（a1，a2）REPS 试验；（b1，b2）Cons-w1 试验：（c1，c2）Cons-w2 试验Fig. 5 Horizontal distribution of the 500-hPa meridional wind perturbations at initial time (left column) and 24 h forecast time (right column): (a1, a2)Expt REPS; (b1, b2) Expt Cons-w1; (c1, c2) Expt Cons-w2

图6 是850 hPa 纬向风的集合初始扰动REPS（图6a1、图6b1 和图6c1）和分析约束扰动（图6a2、图6b2 和图6c2）的分布，其中阴影表示地形。与500 hPa 初始扰动相比，对流层低层850 hPa 的纬向风扰动量值较小，同样主要集中于气旋周围、切变线附近、暴雨区以及高原附近。类似于经向风扰动，初始时刻的纬向风扰动（图6a1）经分析约束后，中小尺度集合扰动的物理结构和扰动振幅均得到不同程度的有效调整，约束方案Cons-w2（图6c1）的扰动振幅同样略小于约束方案Cons-w1（图6b1），其扰动结构也得到更加有效的调整，与天气形势更加一致。经过24 h 积分后，分析约束方案Consw2的暴雨区预报扰动无论扰动结构和振幅都具有合理演变和快速增长发展，与剧烈变化的中小尺度天气形势发展相一致（图6c2），尤其高原东侧快速发展的预报扰动和北方低涡扰动的结构和振幅的演变，具有更加明显的流依赖特征。约束方案Cons-w1的预报扰动也呈现出较合理的增长和演变特征，但相对于方案Cons-w2的效果则次之。无约束REPS 方案的24 h 预报扰动的增长和结构演变特征，在高原东侧和北方低涡附近呈现的中小尺度扰动信息明显不足。这进一步表明，分析约束的预报扰动具有更强的表征对流层低层中小尺度扰动信息的能力，尤其约束方案Cons-w2的效果更优。

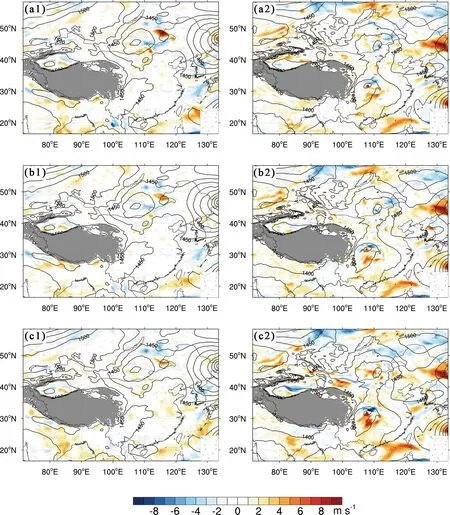
图6 850 hPa 纬向风初始扰动（左列）与24 h 预报扰动（右列）的水平分布：（a1，a2）REPS；（b1，b2）Cons-w1；（c1，c2）Cons-w2Fig. 6 Horizontal distribution of the 850-hPa zonal wind perturbations at initial time (left column) and 24 h forecast time (right column): (a1, a2) Expt REPS; (b1, b2) Expt Cons-w1; (c1, c2) Expt Cons-w2

4.1.2 集合扰动的垂直结构特征

为了全面分析集合扰动增长和发展演变的三维空间结构，从而对分析约束方案的效果有更准确的理解，在认识风场扰动水平结构和振幅及其演变的基础上，进一步分析质量场温度扰动的垂直结构和传播特征。基于本次天气过程中低槽以及切变的位置，图7 给出了REPS 和分析约束方案Cons-w1和Cons-w2的温度扰动沿110°E 的垂直结构。原始初始扰动REPS（图7a1）在50°N 附近的对流层中上层300 hPa 和近地面层附近的温度扰动振幅显著偏大，而对流层中层的扰动偏小，而经24 h 预报后，随着天气系统的发展和移动，该区域上空的温度扰动基本消失，只有南侧上空衍生了振幅较小的温度扰动（图7a2）。总起来看，REPS 初始扰动和24 h预报扰动结构不够完整，振幅变化不连续，与实际天气系统的发展不一致。

经约束方案Cons-w1（图7b1）和Cons-w2（图7c1）分析约束后，其相应位置和高度的温度初始扰动的中小尺度扰动得以合理表征，其扰动振幅也均得到较明显的缩小调整，尤其在对流层中层附近弥补了REPS 初始扰动所不具备的中小尺度扰动信息，使得该区域的温度初始扰动与其中小尺度天气系统的剧烈发展更加吻合。另外，约束后对流层中上层和近地层扰动振幅较大的虚假扰动得以有效控制，基本剔除了该虚假扰动信息，而且分析约束方案Cons-w2对REPS 初始扰动的调整优化效果较约束方案Cons-w1更加显著。这进一步说明，分析约束方案在保留原温度扰动有效信息的前提下，具有优化温度扰动结构、有效消除不合理偏大扰动振幅的效果，同时还具备有效弥补中小尺度扰动信息不足的能力，尤其分析约束方案Cons-w2的效果更为明显。

分析约束的24 h 预报扰动的增长和物理结构演变呈现出与中小尺度天气系统发展演变基本相一致的特征。相对于REPS 的24 h 预报扰动，约束方案Cons-w1（图7c2）在中纬度45°N 附近对流层低层的预报扰动增长更快，对流层中上层的扰动振幅和结构都优于前者。而约束方案Cons-w2的中纬度对流层低层的预报扰动振幅增加更明显，呈现出扰动增长更快的趋势，且中小尺度扰动结构更加清晰；对流层中高层的预报扰动振幅的结构性增长更为明显（图7c2）。这表明更加合理的约束方案Cons-w2初始扰动在预报过程中，其预报扰动的空间物理结构具有更加合理的反映随天气形势快速变化的连续性演变能力，既能再现中大尺度预报扰动的斜压性结构特征，又能够合理的表征中小尺度预报扰动的空间结构和振幅的增长，相对于约束方案Cons-w1呈现出更优的预报效果。

图7 温度初始扰动（左列）与24 h 预报扰动（右列）沿110°E 的垂直剖面：（a1，a2）REPS 试验；（b1，b2）Cons-w1 试验；（c1，c2）Cons-w2 试验Fig. 7 Vertical cross sections of initial perturbations (left colum) and 24 h forecast perturbations (right column) of the temperature field along 110°E:(a1, a2) Expt REPS; (b1, b2) Expt Cons-w1; ( c1, c2) Expt Cons-w2

从约束前后经向风初始扰动及其对应的24 h预报扰动增长和演变的垂直结构（图8）来看，其预报扰动的增长及其结构演变与相应天气系统的发展也同样具有更加一致的协同性。初始扰动REPS中经向风扰动的大值区主要位于100°E～115°E 区域的对流层中上层和中下层，扰动振幅较为明显，但三维空间的扰动结构不够连续（图8a1）。而分析约束的初始扰动（图8b1、图8c1），其局部扰动振幅略有减小，但中小尺度天气系统的三维扰动结构刻画的更为清晰，尤其对流层中层的扰动信息更加丰富，其结构的连续性和完整性与中小尺度天气系统更加协调一致。相较初始时刻，分析约束对应的24 h 预报扰动随中层冷涡和低层低涡系统以及其他中小尺度天气系统的快速发展，预报扰动在高度层不断延伸发展，并向下游传播（图8b2 和图8c2），尤其Cons-w2约束方案对应的预报扰动传播速度最快，扰动结构更为连续和完整（图8c2）。

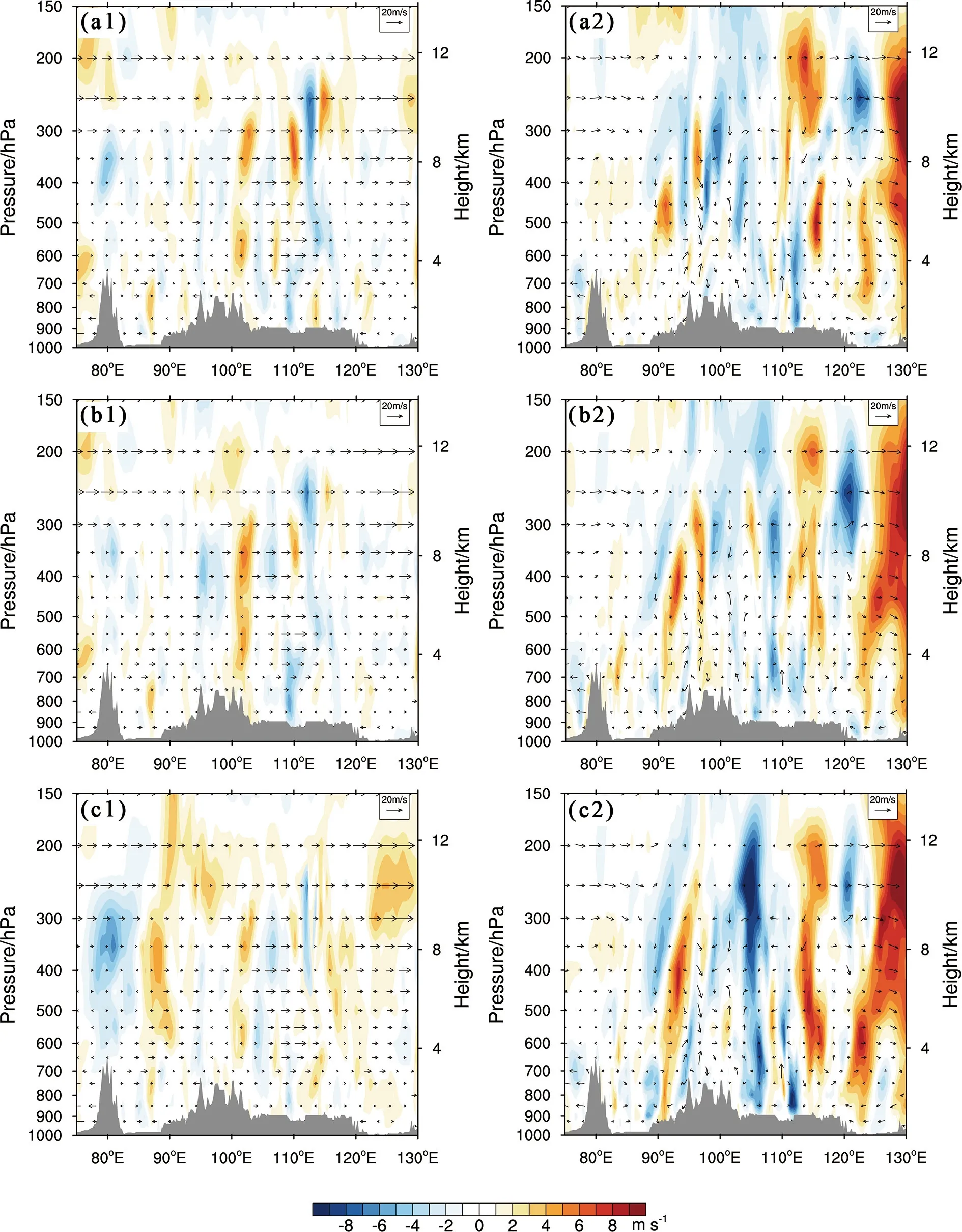
图8 经向风初始扰动（左列）与24 h 预报扰动（右列）沿45°N 的垂直剖面：（a1，a2）REPS 试验；（b1，b2）Cons-w1 试验；（c1，c2）Cons-w2 试验Fig. 8 Vertical cross section of initial perturbations (left column) and 24 h forecast perturbations (right column) of the meridional wind along 45°N:(a1, a2) Expt REPS; (b1, b2) Expt Cons-w1; (c1, c2) Expt Cons-w2

尽管分析约束前的径向风初始扰动振幅较分析约束扰动大，但由于初始结构不尽合理，不能准确表征快速发展的中小尺度天气系统，其预报扰动依然难以描述天气系统的快速发展特征。分析约束的初始扰动结构和振幅其更趋于合理，使得其预报扰动能够更好的表征出中小尺度天气系统的发展演变，尤其Cons-w2分析约束方案效果更为明显。

不论是从集合扰动的水平结构还是垂直结构均能看出，分析约束方案对集合初始扰动的结构和振幅都具有良好的调整效果，能够更加合理、细致的的表征中小尺度天气系统对应的扰动信息，从而其预报扰动也能够与实际天气系统的发展和演变更加吻合。由于Cons-w2约束方案约束函数能够针对集合扰动的合理性程度进行自主调整，使得约束后的扰动既充分保留了原扰动中合理的信息，又可以吸收分析不确定性的合理信息，对不合理的扰动结构和振幅进行适应性调整，从而获得扰动结构和振幅均更优于原REPS 和Cons-w1约束方案的集合初始扰动。

4.2 集合离散度的时间演变

集合离散度可以衡量集合预报的整体性能，其发展演变的合理性能够反映集合初始扰动的质量。合理的集合离散度不仅在量值上与集合预报均方根误差相当，其空间结构也应该与之基本吻合。过大的集合离散度难以合理表征可能的大气运动状态的预报误差而降低集合预报的整体质量；过小则会导致各集合成员趋于相同，失去集合预报的意义。

分析约束前后中纬度地区各气压层纬向风集合离散度随预报时间的发展演变（图9）显示，约束前后纬向风离散度均随预报时间呈现稳定发展的趋势，且高层离散度的增长相对较大，低层较小且增长较缓，与预报误差的总体增长趋势基本吻合。分析约束前REPS 的初始离散度较大，在预报的前12 h 内缓慢减小再开始增长（图9a）。显然，这一缓慢减小过程与模式初值和模式不完全协调有关，更重要的原因应该是该初始扰动的结构和振幅不合理产生虚假扰动信息有直接关系；分析约束初始扰动的离散度尽管总体上变化不大，但对流层中高层的增长速率明显增加，中低层也略有改善，特别是预报前12 h 的离散度均呈现一致性的增长，消除了原先降低再增长的问题（图9b 和图9c）。值得注意的是，分析约束Cons-w2方案（图9c）在前12 h 预报阶段的对流层中低层离散度增长较Consw1方案（图9b）更为快速，也表明分析约束Consw2方案的更优效果。

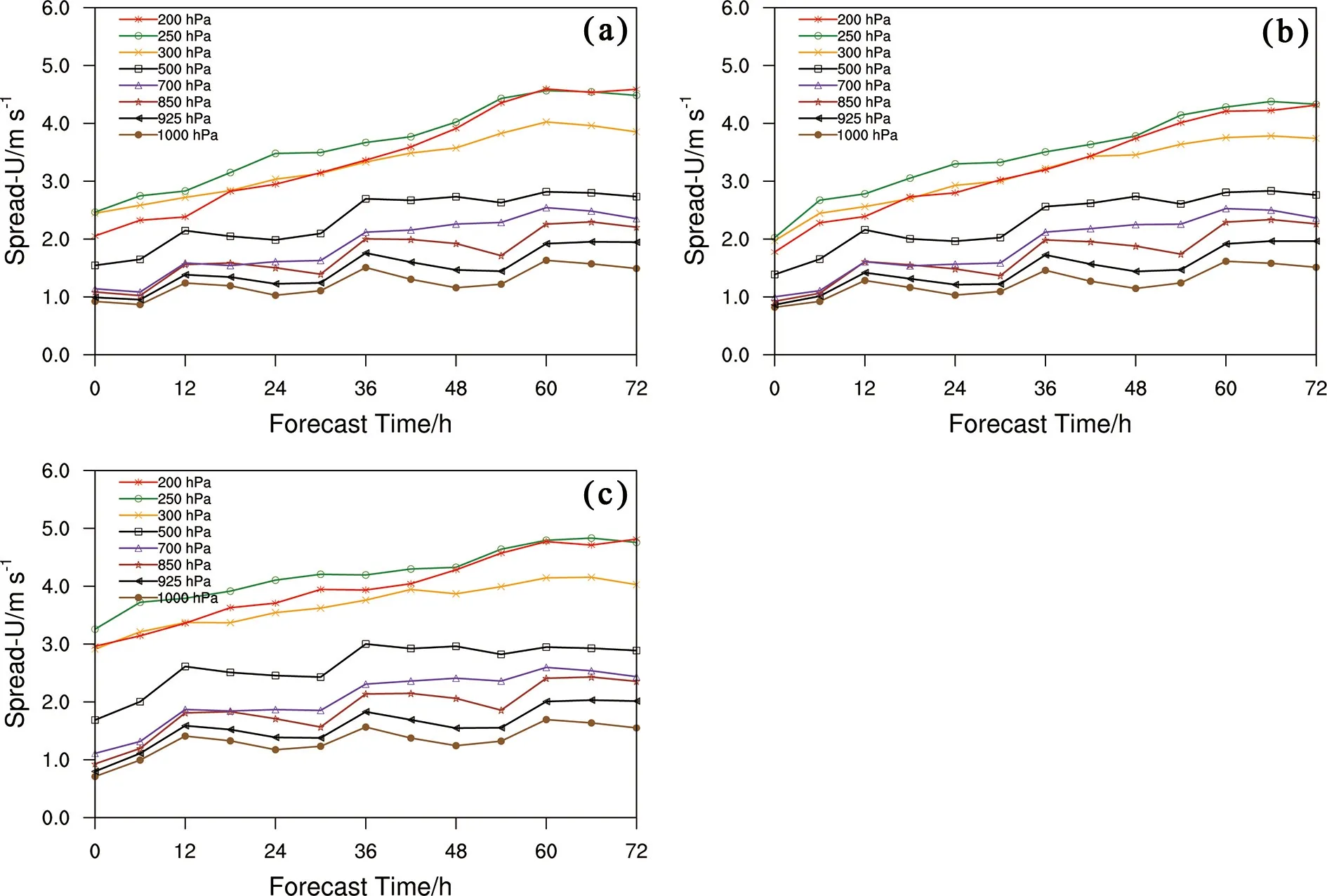
图9 中纬度地区（30°N～45°N，71.5°E～133.6°E）各气压层纬向风的集合离散度随预报时间的演变：（a）REPS 试验；（b）Cons-w1 试验；（c）Cons-w2 试验Fig. 9 Evolution of the ensemble spread of zonal winds in each pressure layer at middle latitudes (30°N-45°N, 71.5°E-133.6°E) with forecast time:(a) Expt REPS; (b) Expt Cons-w1; (c) Expt Cons-w2

纬向风离散度垂直结构的时间演变（图10）也显示，分析约束前后对流层中层离散度增长缓慢，低层和高层增长相对较快，且在250 hPa 附近存在一个离散度及其增长的锋值。另外，不同预报时段离散度的增长不尽一致。REPS 方案在积分6 h 后300 hPa 高度以下的离散度基本无变化，反映了其初始扰动的不合理性，导致离散度难以增长（图10a）；而经分析约束方案Cons-w1（图10b）和Cons-w2（图10c）约束调整后，虚假扰动信息被有效削减，其初始扰动更加趋于合理，从而使得各高度层纬向风离散度在积分6 h 后均明显增加。相较于约束方案Cons-w1，Cons-w2方案的离散度在各个层次上的增长更加趋于稳定，随高度增加而增大的趋势更为明显。

综上分析可见，分析约束的初始扰动由于吸收了分析增量信息对原集合扰动的结构和振幅进行了合理调整，消除了部分虚假扰动信息，能够更准确地反映预报的不确定性，其离散度的演变也自然呈现出更为合理的增长状态。这进一步反映了借助分析增量信息对元集合初始扰动进行分析约束的有效性和必要性。

4.3 扰动能量的演变特征

集合预报扰动能量特征可以整体上反映集合扰动随预报时间的增长和演变的合理性。扰动总能量的具体表达式为

图11 为分析约束前后集合预报扰动总能量不同预报时刻的垂直分布。类似于集合离散度的垂直结构（图10a），由于初始扰动中存在虚假成分，REPS 的扰动能量在前24 h 预报时间内的增长混乱，尤其对流层中高层积分6 h 后出现明显减小，其他层次也增长极为缓慢。这在很大程度上反映出该初始扰动的结构或振幅的不合理性（图11a）。分析约束调整后，两种方案的初始扰动均呈现出良好的改善效果。尽管分析约束Cons-w1方案的对流层中下层前6 h 预报时间扰动能量的增长依然不尽合理，但对流层中上层已基本合理（图11b）。分析约束Cons-w2方案的前24 h 预报时间内，其整层扰动能量的发展已趋于合理，尤其前6 h 的扰动能量已呈现出合理的快速增加的发展趋势（图11c）。这进一步反映了分析约束方案对调整集合初始扰动的质量具有良好的效果。从构成扰动总能量的扰动动能和扰动内能（图略）可以发现，分析约束扰动方案主要是通过扰动动能对虚假能量进行合理调整，消除不合理扰动信息，且显示出Cons-w2方案的效果更优。然而，分析约束扰动方案并未对不合理的扰动内能起到明显的调整作用。这也是分析约束方案需要进一步完善和优化的工作。

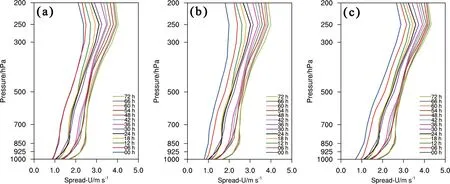
图10 区域（16.5°N～58.35°N，71.5°E～133.6°E）平均的纬向风集合离散度垂直结构随预报时间的演变：（a）REPS 试验；（b）Cons-w1试验；（c）Cons-w2 试验Fig. 10 Evolution of the vertical structure of the regional averaged ensemble spread of zonal winds with forecast time (the region refers to 16.5°N-58.35°N, 71.5°E-133.6°E): (a) Expt REPS; (b) Expt Cons-w1; (c) Expt Cons-w2

图11 区域（16.5°N～58.35°N，71.5°E～133.6°E）平均集合扰动总能量的垂直分布：（a）REPS 试验；（b）Cons-w1 试验；（c）Cons-w2试验Fig. 11 Vertical distribution of the averaged total energy of ensemble perturbations (the region refers to 16.5°N-58.35°N, 71.5°E-133.6°E): (a) Expt REPS; (b) Expt Cons-w1; (c) Expt Cons-w2

5 结论与讨论

本文基于GRAPES 区域集合预报系统，结合不同尺度天气系统的分析误差结构，发展构建了集合预报初始扰动再次优化调整的分析约束方案。通过分析约束前后基本物理量的集合扰动、集合离散度和扰动能量等结构和演变特征的对比分析，评估了分析约束扰动方案的效果，得出以下结论：（1）分析增量包含有观测不确定性和预报不确定性信息，能够合理的反映中小尺度天气系统预报误差结构的演变和振幅增长，与集合扰动所表征的预报不确定性具有良好一致性。（2）基于资料同化的分析增量和集合初始扰动结构和振幅的特点，发展建立的分析约束方案能够有效吸收分析不确定性的有效信息，对集合预报初始扰动的物理结构和扰动振幅具有良好的调整能力，且在保留合理集合扰动信息的基础上，具有消除不合理虚假扰动信息的良好效果，尤其分析约束方案Cons_w2的约束效果明显优于Cons_w1方案。（3）初始扰动经分析约束调整后，两种分析约束方案的风场与质量场预报扰动的结构和振幅得以合理改善，与天气系统的预报误差的发展和演变更加一致，其预报扰动的离散度和扰动能量的增长与演变特征更加符合大气运动状态的预报不确定性，其中分析约束方案Cons_w2的效果更加显著，明显优于约束方案Cons_w1。

本文提出的分析约束方案对改进集合初始扰动质量进行了有益的探索。尽管该分析约束方案呈现了良好的效果，尤其约束方案Cons_w2对不合理扰动的调整能力更优于基于常值分析约束函数的Cons_w1方案。但总体上看，其有效性更多的表现在前24 h 预报时间，而且对流层低层虽有改善，但依然不够理想，这也反映出调整后的集合初始扰动依然包含有不同程度的不合理信息。当前分析约束方案仅是对初始扰动不合理区域的局部调整，这可能也是影响分析约束的集合扰动效果维持预报时间偏短的主要原因。因此，继续完善和优化分析约束函数的性能，构建具有完全自适应能力的分析约束函数是需要进一步研究的关键科学问题。同时，深入考察初始扰动和预报扰动包含的中小尺度扰动结构特征及其发展、演变规律对构造合理的高分辨集合预报扰动场也具有重要意义。