非线性温差对大跨度钢结构采光顶影响研究——以南宁地区为例

□ 周 凯

现代建筑中的钢结构屋顶应用越来越广泛。由于钢结构其自身易加工的特性，能够满足现代建筑的复杂造型需求，同时钢结构轻质高强，抗震性能良好，也广泛应用于大跨度结构体系中。但由于钢结构自身材料的特性，其对温度较混凝土等结构敏感，特别是对于露天钢结构的构架、钢结构的玻璃采光顶等阳光能直接照射的钢结构而言，其温差效应是不能被忽略的。目前对均匀温差的影响已有共识，但是在考虑非线性温差之后对钢结构的影响有多大，还没有具体的案例说明。

自然环境中因太阳辐射、构件表面的吸热性，以及环境温度、风力、天气等都影响着非线性温差的取值，所以每个地区的取值并不一样。本文选取了南宁地区一个大跨度钢结构采光顶屋面的实际工程，通过考虑南宁地区非线性温差和不考虑非线性温差两种情况进行计算分析对比，得出相关的结论。

1 非线性温差的计算原理

1.1 非线性温差自应力计算

非线性温差与均匀温差作用在钢结构上的原理有明显差别。均匀温差作用在钢构件内任何一点的温度变化都是一致的，这种温差会引起整个钢构件的整体收缩或者延伸，如果钢构件的两端没有任何约束，那么均匀温差只会让钢构件产生位移而不会产生内力。而非线性温差是由于沿构件的高度或者宽度方向温度的变化呈现非线性的变化，在太阳光的照射下，钢构件内部和表面存在着明显的温度差，即钢构件表面快速升温，而钢构件内部升温滞后，造成钢构件的表面与内部温度变化不一致，呈非线性变化。当温度变化时，材料会发生热胀冷缩，因为钢构件各层温度的不同，所产生的应变也不同，其应变会受到结构内部互相约束而产生温度自应力，即不管构件两端有没有约束，构件都会产生自应力。这种自应力有3个特点[1]：一是它不同于一般荷载产生的应力。其应力应变不是简单的符合胡克定律，而会出现大应力小应变和小应力大应变的情况，但是它仍然符合伯努利的平面变形规律，温差应力与温差应变和温度自由应变差成正比。二是由于这种温差沿厚度方向成非线性分布，故在钢构件截面上的温度应力也是分线性分布的。三是因为钢结构中的温度瞬间变化，故在结构中产生的温度应力也随时间变化，具有明显的时间性。

假定等截面钢构件上温度变化规律一样，温度变化函数为T（x，y），当没有纵向约束的时候，单位积分面积上的形变为[2-3]：

式（1）中：α—材料线性膨胀系数

若截面和温度变化都对称于y轴，在平截面假定下，则截面变形为：

式（2）中：0ε—截面y=0处的应变

ψ—单元段变形后的曲率

y—任一点坐标

则受到纵向约束的应变（σε）与约束应力可写为：

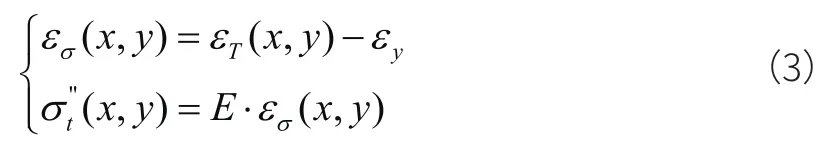
式（3）中：E—材料的弹性模量

根据应力、应变可以写出截面的弯矩、轴力方程：

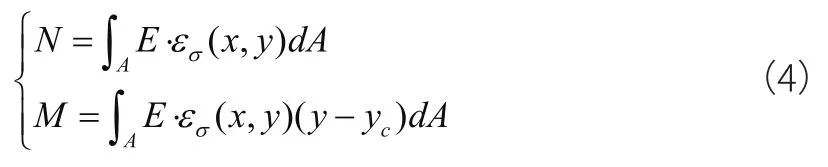
式（4）中：yc—截面中性轴坐标

由于钢构件截面上没有外荷载，根据内力平衡条件，令M=0，N=0代入式子就可以求出温度自应力。

当我们只考虑钢构件截面一个方向的非线性温度场时（比如纵向），上面的式子中的积分就对y轴进行积分。则式（2）中的0ε、ψ可写为：

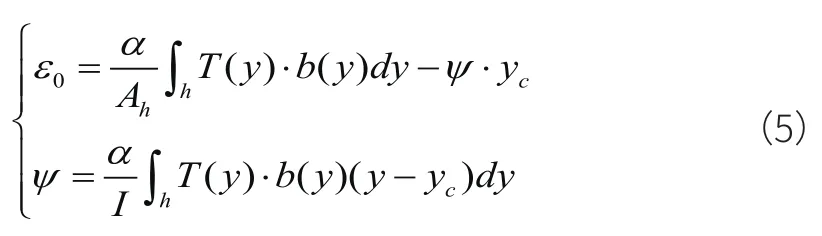
式（5）中：T(y)—温度沿y轴方向的变化函数

b(y)—截面宽度沿y轴方向的变化

Ah—截面面积

I—截面抗弯惯性矩

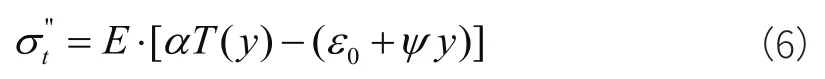
1.2 温度次应力计算[2-3]

将式子（4）中的0ε、ψ看成是由等效线性温差引起的形变和曲率，根据结构力学知识。其力法方程为：

将式（8）代入式2-7解出Xi，得出拱圈任意截面的温度次内力：

截面上温度次应力表达式为：

2 南宁地区钢结构非线性温差的取值

2.1 南宁地区钢结构非线性温差的实验简述

为获得南宁地区非线性温差的取值数值。选择在广西建设职业技术学院5号教学楼8楼的屋顶，从2020年7月1日至2020年12月31日连续对工字型钢和箱型钢构件在露天条件下实际温差进行测试。试验构件没有其他建筑物遮挡，全天可以接受阳光照射，构件下部用砖块加高，保证正常通风状态，构件材料采用Q235B，实验条件如图1、图2所示，构件尺寸及厚度以及测温点如图3、图4所示。

图1 构件阳光照射图

图2 构件试验图

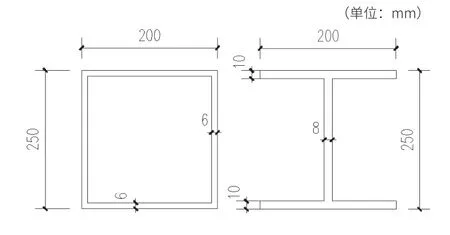
图3 试验构件尺寸图

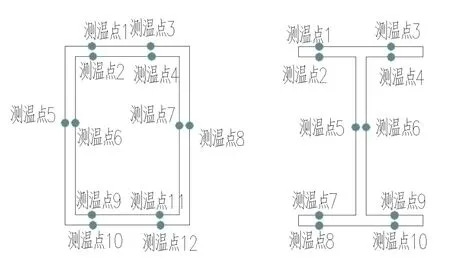
图4 构件测温点布置图

2.2 南宁地区钢结构非线性温差的取值结果简述

根据实验结果，结合王元清，林错错等对露天日照条件下钢结构构件温度的试验研究[4-5]以及本人前期的相关研究成果，非线性温差的取值以半年内构件测得的构件同一天中最大温差值。取构件中的上翼缘、中翼缘、下翼缘3处的温度值中温差最大时刻的最低温为基础温差的0℃点，考虑到测量误差及构件表面条件，偏于安全的取整数值。南宁地区工字型构件和箱型构件的非线性温差的最终取值，分别如图5、6所示。

图5 南宁地区工字型构件非线性温差取值

3 工程概况

某体育馆坐落南宁市高新区，建筑面积5291m2，地上4层，地下1层，建筑最高点标高为20m，跨度28m。主体结构采用混凝土框架结构，大跨度屋面采用箱型钢结构玻璃采光顶。钢材采用Q345B。主钢梁采用口500×300×10×12，次钢梁采用口450×250×10×10，支座周边钢梁采用口300×200×6×6，钢梁支座采用口400×400×16×16，直接焊接在混凝土的预埋板上。

4 建模计算

4.1 有限元模型

本工程的计算软件采用Midas Gen大型有限元计算软件。建模计算采用整体建模的方式，将下部的混凝土部分跟上部的钢结构屋面部分整体建模，整体计算。如图7所示。

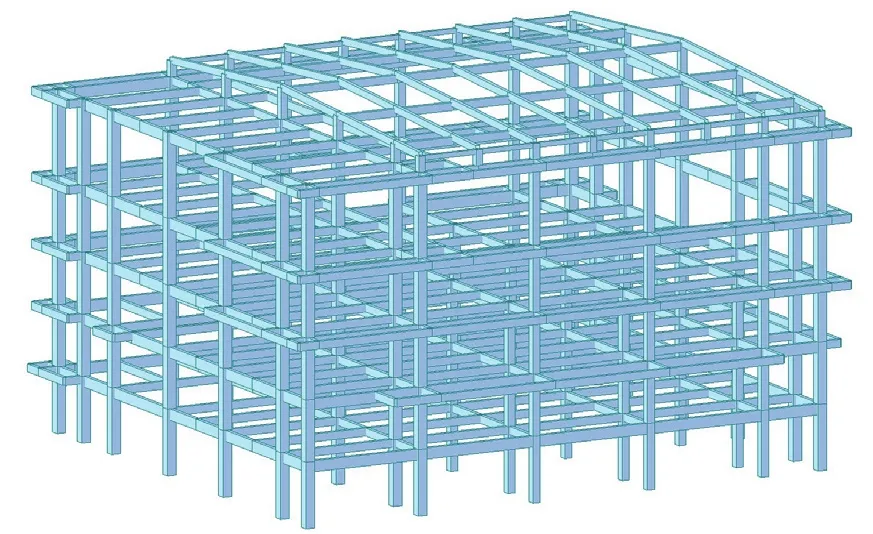
图7 整体有限元建模模型

4.2 计算条件及荷载组合

本工程玻璃容重加配件荷载取0.50kN/㎡，基本风压0.35kN/㎡，地面粗糙类别为B类。本工程抗震设防烈度为7°、设计基本地震加速度值为0.10g，设计地震分组为第一组，场地土类别为Ⅱ类场地土；阻尼比混凝土结构取0.05，钢结构部分取0.02。钢结构部分考虑均匀升温或降温作用T=+35℃/T= -35℃的温差作用。非线性温差的取值采用箱型构件的取值，详见图6所示。

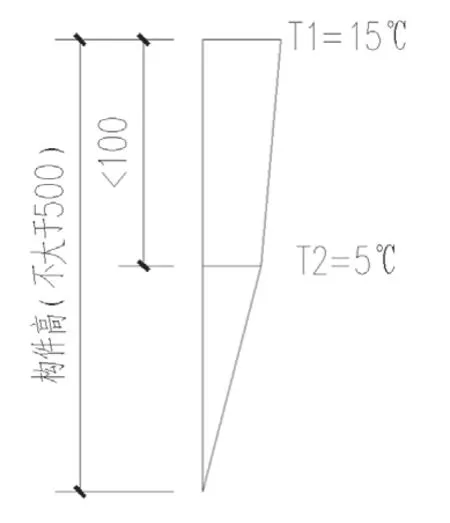
图6 南宁地区箱型构件非线性温差取值

本工程的设计依据《建筑结构荷载规范》（GB 50009—2012）[6]，其荷载组合系数也按照该规范取用。

4.3 非线性温差的加载

本工程的非线性温差的加载采用Midas Gen软件中“梁截面温度”[7]模块加载，加载数值按照图6所示，500mm高的钢箱梁上翼缘近似的取升温15℃，下翼缘近似的取升温0℃，中间腹板按照图6数值内插取值；其他高度的截面按照图6的数值内插取值。

5 计算结果分析

5.1 非线性温差对变形的影响

当只考虑非线性温差作用的时候，通过计算整个玻璃屋顶钢结构在竖向的位移向上可达0.031m（向上），在水平两个方向的位移最大可达0.009m，如图8所示。可见考虑非线性温差对于大跨度采光顶而言，主要影响其竖向的位移，水平位移影响不大。就本工程而言，其对竖向位移的影响程度可达短跨的1/903。本工程恒载+活载引起的跨中位移为0.120（向下），非线性温差产生的位移与恒载+活载产生的位移方向相反，但是跟风吸产生的竖向位移同向。

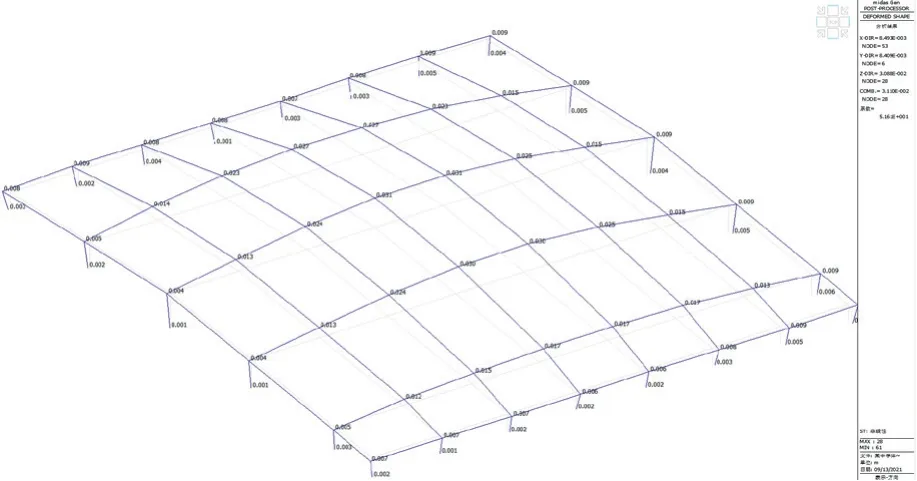
图8 只考虑非线性温差采光顶位移图（单位：m）

5.2 非线性温差对内力的影响

当只考虑非线性温差作用的时候：一是整个玻璃屋顶钢结构的轴力最大为1210.3kN（压力），如图9所示，出现在边跨梁。二是整个玻璃屋顶钢结构的剪力最大为622.1kN，位于支座处，钢梁的最大剪力为101.5kN，出现在边跨梁，如图10所示。三是整个玻璃屋顶钢结构的弯矩最大为858.9kN·m，位于支座处，钢梁的最大弯矩为365.0kN·m，出现在边跨梁，如图11所示。

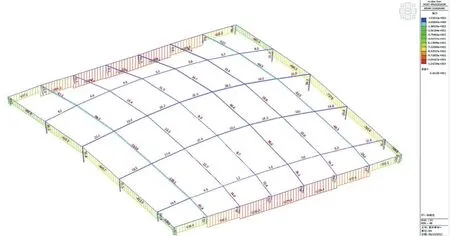
图9 只考虑非线性温差采光顶轴力图（单位：kN）

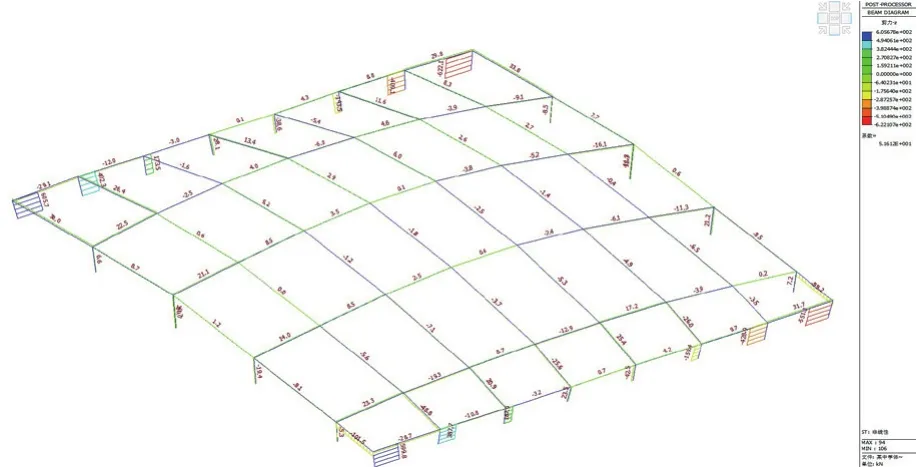
图10 只考虑非线性温差采光顶剪力图（单位：kN）

图11 只考虑非线性温差采光顶弯矩图（单位：kN·m）

为了更直观地看出考虑非线性温差后钢结构采光顶的内力增幅，把考虑非线性温差后钢梁产生最大内力的相应部位的内力值，与恒载+活荷载的组合产生的相应位置的内力值做一个对比，详见表1所示。

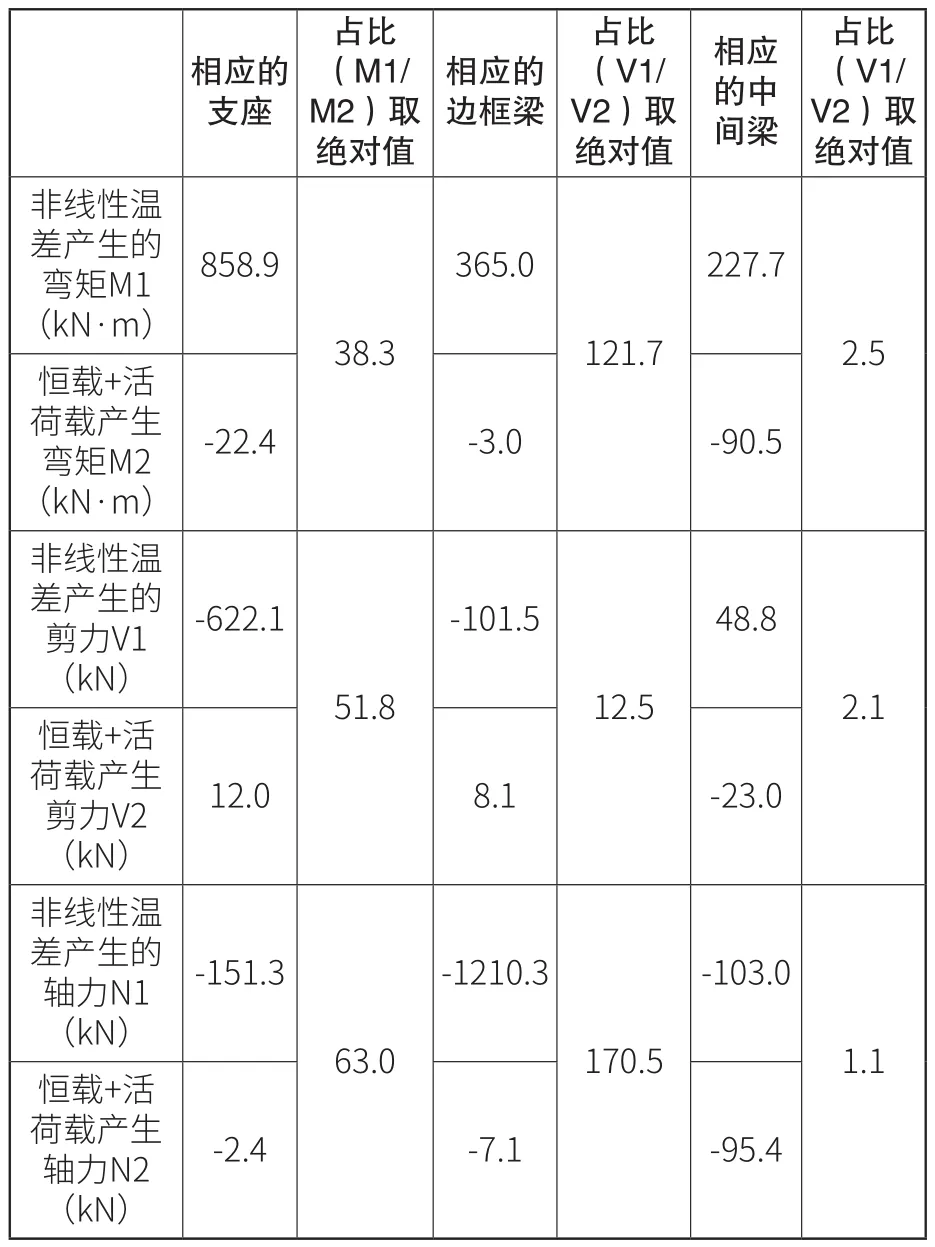
表1 构件考虑非线性温差与恒+活载产生的内力值对比

根据以上结果分析可得如下结论。

（1）考虑非线性温差后，钢框架的支座弯矩最大值可达859.9kN·m，是对应的恒载+活荷载产生弯矩的38倍多，且方向相反，影响较大；钢框架的边梁弯矩最大值可达365.0kN·m，是对应的恒载+活荷载产生弯矩的121倍多，且方向相反，影响最大；钢框架的中间梁弯矩最大值可达227.7kN·m，是对应的恒载+活荷载产生弯矩的2.5倍多，且方向相反，影响明显。

（2）考虑非线性温差后，钢框架的支座剪力最大值可达622.1kN，是对应的恒载+活荷载产生剪力的51倍多，且方向相反，影响最大；钢框架的边梁弯矩最大值可达101.5kN，是对应的恒载+活荷载产生剪力的12倍多，且方向相反，影响较大；钢框架的中间梁剪力最大值达48.8kN，是对应的恒载+活荷载产生剪力的2倍多，且方向相反，影响明显。

（3）考虑非线性温差后，钢框架的支座轴力最大值可达151.3kN，是对应的恒载+活荷载产生轴力的63倍多，方向一致，影响较大；钢框架的边梁轴力最大值可达1210.3kN，是对应的恒载+活荷载产生轴力的170倍多，方向一致，影响最大；钢框架的中间梁轴力最大值达103.0kN，是对应的恒载+活荷载产生轴力的1.1倍多，方向一致，影响明显。

5.3 考虑非线性温差组合对应力比的影响

当考虑非线性温差作用时，再把均匀温差跟非线性温差同时考虑后，按照《建筑结构荷载规范》（GB 50009—2012）的荷载组合进行设计计算。计算结果详表2所示。

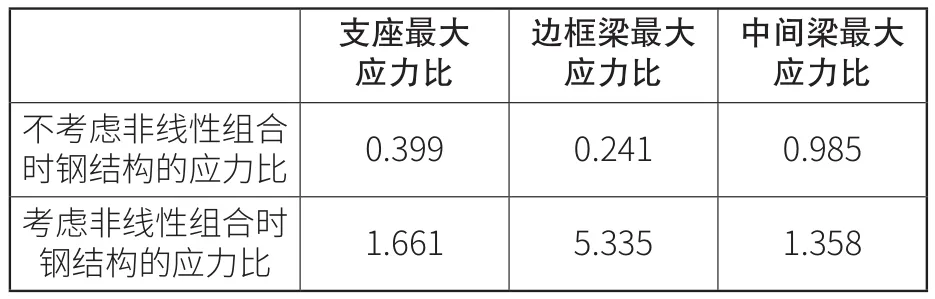
表2 构件考虑非线性温差与不考虑非线性温差构件应力比

从以上可以看出当考虑非线性温差的时候，其对钢框架采光顶的边框梁影响最大，其最大的应力比可以达到5倍多，远超钢结构本身的强度值。支座及中间梁的最大应力比也分别达到1.6倍与1.3倍多，由此可见，非线性温差对于大跨度钢结构屋面影响较大，有必要计入计算或者采取相应的措施减少非线性温差的影响。

6 结论与建议

本文选择南宁地区的一个大跨度钢结构采光顶为计算案例，以南宁地区非线性温差的实测值进行加载计算，与不考虑非线性温差的结果进行对比分析，得出以下结论。

（1）日照条件下，非线性温差对于钢结构屋面主要发生明显的竖向向上的位移，该位移方向与恒载、活载所产生的位移方向相反，与风吸产生的竖向变形位移方向同向，在设计、施工中应该给予考虑。

（2）从本工程的案例计算中可以看出，考虑非线性温差后，对钢结构的内力影响较大。其中对边框梁影响最大，其次是支座，最后是中间框梁，这是由于边框梁与支座链接，其约束较为密集，非线性温差引起的温度自应力与温度次应力叠加的影响导致的。

（3）将均匀温差与非线性温差一起纳入荷载组合进行设计计算后发现，对整体钢结构框架的应力比影响较为明显，且越接近支座和边框梁影响的越大。

（4）本文中南宁地区非线性温差的试验构件并没有考虑到钢结构中涂装的问题，因为钢结构防火、防腐的不同做法对钢结构表面温度的影响是不一样的。因本文中的非线性温差试验并没有考虑钢结构的涂装问题，这与钢结构采光顶的施工安装或使用期间表面涂装损坏脱落后的钢结构构件状态接近，因此得出的试验数据是偏于安全的，从而其非线性温差的取值也是偏于保守。从以上的试算结果来看，非线性温差对钢结构的影响较大，因此对于大跨度钢结构的采光顶或受阳光照射的钢结构屋面，有必要考虑非线性温差的影响。而且在设计中应该适当考虑支座的约束条件，适当的释放一些支座约束，减少非线性温差产生的温度次内力的影响，确保钢结构屋面的安全度。