Evaluating the Risk of Disclosure and Utility in a Synthetic Dataset

Kang-Cheng Chen,Chia-Mu Yuand Tooska Dargahi

1Industrial Technology Research Institute,Hsinchu,310,Taiwan

2National Chiao Tung University,Hsinchu,320,Taiwan

3University of Salford,Manchester,M5 4WT,United Kingdom

Abstract: The advancement of information technology has improved the delivery of fnancial services by the introduction of Financial Technology(FinTech).To enhance their customer satisfaction,Fintech companies leverage artifcial intelligence(AI)to collect fne-grained data about individuals,which enables them to provide more intelligent and customized services.However,although visions thereof promise to make customers’ lives easier, they also raise major security and privacy concerns for their users.Differential privacy(DP)is a common privacy-preserving data publishing technique that is proved to ensure a high level of privacy preservation.However,an important concern arises from the trade-off between the data utility the risk of data disclosure(RoD), which has not been well investigated.In this paper, to address this challenge,we propose data-dependent approaches for evaluating whether the suffcient privacy is guaranteed in differentially private data release.At the same time, by taking into account the utility of the differentially private synthetic dataset, we present a data-dependent algorithm that, through a curve ftting technique, measures the error of the statistical result imposed to the original dataset due to the injection of random noise.Moreover, we also propose a method that ensures a proper privacy budget, i.e., ∊will be chosen so as to maintain the trade-off between the privacy and utility.Our comprehensive experimental analysis proves both the effciency and estimation accuracy of the proposed algorithms.

Keywords: Differential privacy; risk of disclosure; privacy; utility

1 Introduction

Financial Technology (FinTech) concept has evolved as a result of integrating innovative technologies into fnancial services, e.g., AI and big data, Blockchain and mobile payment technologies, to provide better fnancial services [1].Investments in FinTech industry is trending upward, such that by September 2020 the global investment in Fintech was $25.6 Billion, reported by KPMG [2].However, security and privacy of the users’ data is among the main concerns of the FinTech users [3].Data governance and user data privacy preservation are reported as the most important challenges in FinTech due to the accessibility of user data by suppliers and third parties [3].Some fnancial institutions rely on honest but curious FinTech service providers which might be interested in accessing sensitive attributes of users’ data.Specially, in the case of small and medium businesses, which provide personalized fnancial services to their customers,with no background knowledge in security and data privacy, protection of users’ data becomes even more challenging.

The “open data”concept and data sharing for banking industry has been promoted by several countries, including the UK.A report by the Open Data Institute, discusses the benefts of sharing anonymized bank account data with the public and suggests that such data release could improve customers decision making [4].User data are usually shared with the data consumers via data release; herein, we consider scenarios in which data are released, i.e., where tabular data with numeric values (which could be related to user’s bank transactions, stock investments, etc.)are to be published (or shared) by the data owner.However, data release often presents the problem of individual privacy breach, and there has always been a debate between data privacy and openness, reported by Deloitte [5].A real-world example thereof is that, by using publicly available information, researchers from the University of Melbourne were able to re-identify seven prominent Australians in an open medical dataset [6].Furthermore, researchers from Imperial College London found that it would be possible to correctly re-identify 99.98% of Americans in any dataset by using 15 demographic attributes [7].Other relevant privacy incidents were also reported [8,9].All of these incidents provide evidence of privacy leakage because of improper data release.

Recently, the United States and Europe launched new privacy regulations such as the California Consumer Privacy Act (CCPA) and General Data Protection Regulation (GDPR) to strictly control the manner in which personal data are used, stored, exchanged, and even deleted by data collectors (e.g., corporations).Attempts to assist law enforcement have given rise to a strong demand for the development of privacy-preserving data release (PPDR) algorithms, together with the quantitative assessment of privacy risk.Given an original dataset (the dataset to be released),PPDR aims to convert the original dataset into a sanitized dataset (or a private dataset) such that privacy leakage by using the sanitized dataset is controllable and then publish the sanitized dataset.In the past, the former demands could be satisfed by conventional approaches such ask-anonymity,l-diversity, andt-closeness.However, these approaches have shortcomings in terms of syntactic privacy defnition and the diffculty in distinguishing between quasi-identifers and sensitive attributes (the so-called QI fallacy), and therefore are no longer candidates for PPDR.In contrast, differential privacy (DP) [10] can be viewed as a de-facto privacy notion, and many differentially private data release (DPDR) algorithms [11] have been proposed and even used in practice.Note that DPDR can be considered as a special type of PPDR with DP as a necessary privatization technique.

Although it promises to maintain a balance between privacy and data utility, the privacy guarantee of DPDR is, in fact, only slightly more explainable.Therefore, in the case of DPDR,it is diffcult to choose an appropriate confguration for the inherent privacy parameter, privacy budget∊.More specifcally, DP uses an independent parameter∊that controls the magnitude of the injected noise, yet the selection of∊such that the data utility is maximized remains problematic.On the other hand, although the value of∊affects the magnitude of noise, it has no direct relevance to the risks of data disclosure, such as the probability of re-identifying a particular individual.In other words, the choice of∊such that the privacy is meaningfully protected still needs to be investigated.In practice, there is no clear recommendation by the regulatory institutions in Fintech industry on the preferred anonymization technique which could address the challenge of preserving privacy while providing openness.This might be due to the unclarity of privacy guarantee versus utility in the existing DPDR algorithms.Thus, a strong demand exists to develop novel measures for the risk of disclosure (RoD) and utility for DPDR.

1.1 Related Work

In this section we present a brief review of studies on the differentially private data release and the risk of disclosure.

1.1.1 Differentially Private Data Release(DPDR)

Privacy-preserving data release (PPDR) methods have been introduced to address the challenge of the trade-off between privacy and utility of a released dataset.Several anonymization and privacy-enhancing techniques have been proposed in this regard.The most popular technique isk-anonymity [12], which uses generalization and suppression to obfuscate each record between at leastk−1 other similar records.Due to vulnerability of thek-anonymity against sensitive attribute disclosure where attackers have background knowledge,l-diversity [13] andt-closeness [14] are proposed to further diversify the record values.However, all of these techniques are proven to be theoretically and empirically insuffcient for privacy protection.

Differential privacy (DP) [10] is another mainstream privacy preserving technique which aims to generate an obfuscated dataset where addition or removal of a single record does not affect the result of the performed analysis on that dataset.Since the introduction of DP, several DPDR algorithms have been proposed.Here, we place particular emphasis on the synthetic dataset approach in DPDR.Namely, the data owner generates and publishes a synthetic dataset that is statistically similar to the original dataset (i.e., the dataset to be released).It should be noted that, since 2020, the U.S.Census Bureau has started to release census data by using the synthetic dataset approach [15].DPDR can be categorized into two types:Parametric and non-parametric.The former relies on the hypothesis that each record in the original dataset is sampled from a hidden data distribution.In this sense, DPDR identifes the data distribution, injects noise into the data distribution, and repeatedly samples the noisy data distribution.The dataset constructed in this manner is, in fact, not relevant to the original dataset, even though they share a similar data distribution, and can protect individual privacy.The latter converts the original dataset into a contingency table, where i.i.d.noise is added to each cell.The noisy contingency table is then converted to the corresponding dataset representation.This dataset can be released without privacy concerns because each record can claim plausible deniability.

Two examples in the category of parametric DPDR are PrivBayes [16] and JTree [17].In particular, PrivBayes creates a differentially private but high-dimensional synthetic datasetDby generateing a low-dimensional Bayesian networkN.PrivBayes is composed of three steps:1) Network learning, where ak-degree Bayesian networkNis constructed over the attributes in the original high-dimensional datasetOusing an(∊/2)-DP algorithm; herekrefers to a small value dependent on the affordable memory size and computational load.2) Distribution learning:an(∊/2)-DP algorithm is used to generate a set of conditional distributions, such that each attribute-parent (AP) inNhas a noisy conditional distribution.3) Data synthesis:Nanddnoisy conditional distributions are used to obtain an approximation of the input distribution, and then from the approximate distribution, we sample tuples to generate a synthetic datasetD.

JTree [17] proposes to use Markov random feld, together with a sampling technique, to model the joint distribution of the input data.Similar to PrivBayes, JTree consists of four steps:1) Generate the dependency graph:The goal of this step is to calculate the pairwise correlation between attributes through the sparse vector technique (SVT), leading to a dependency graph.2) Generate attribute clusters:Once the pairwise correlation between attributes is computed, we use junction tree algorithm to generate a set of cliques from the above dependency graph.These attribute cliques will be used to derive noisy marginals with the minimum error.3) Generate noisy marginals:We generate a differentially private marginal table for each attribute cluster.After that, we also apply consistency constraints to each differentially private marginal table, as a postprocessing, to enhance the data utility.4) Produce a synthetic dataset:From these differentially private marginal tables, we can effciently generate a synthetic dataset while satisfying differential privacy.Other methods in the category of parametric DPDR include DP-GAN [18–20],GANObfuscator [21], and PATE-GAN [22].

On the other hand, Priview [23] and DPSynthesizer [24] are two representative examples in the category of non-parametric DPDR.Priview and DPSynthesizer are similar in that they frst generate different marginal contingency tables.The main difference between parametric and nonparametric DPDR lies in the fact that the former assumes a hidden data distribution, whereas the latter processes the corresponding contingency table directly.Specifcally, noise is applied to each cell of the contingency tables to derive the noisy table.Noisy marginal contingency tables are combined to reconstruct the potentially high-dimensional dataset, followed by a sophisticated design of the post-processing step for further utility enhancement.Other methods in the category of non-parametric DPDR include DPCube [25], DPCopula [26], and DPWavelet [27].

1.1.2 Risk of Disclosure(RoD)Metrics

Not much attention has been paid to develop RoD, although DP has its own theoretical foundation for privacy.The research gap arises because the privacy of DP has been hidden in the corresponding defnition, according to which the query results only differ negligibly from those of neighboring datasets.However, in the real world setting, the user prefers to know whether (s)he will be re-identifed.Moreover, the user wants to know what kind of information is protected,what the corresponding privacy level is, and the potentially negative impact of the perturbation for the statistical analysis tasks.On the other hand, although many DPDR algorithms have emerged,because of the lack of a clear and understandable defnition of RoD, we know that the choice of∊is critical but it hinders the practical deployment of DPDR systems.Thus, we eager to develop an RoD to quantitatively answer questions such as what kind of information is protected, what the corresponding privacy level is, and the potentially negative impact of the perturbation for the statistical analysis tasks properly.

To make the privacy notion easy to understand by layperson, Lee et al.[28] made the frst step to have a friendly defnition of the RoD.They adopt the cryptographic game approach defne the RoD.Specifcally, given a datasetOwithmrecords, the trusted server randomly determines,by tossing a coin, whether a recordr∈Owill be deleted.LetDbe the resulting dataset after the deletion of the chosen record.The attacker’s objective is to determine whether the recordrexists.Here, the attacker is assumed to be equipped with an arbitrary knowledge of the datasetsOandD.In this sense, Lee and Clifton formulated the attacker as a Bayesian attacker, which means that the attacker is aimed to maximize the probability of guessing correctly by using both the prior and posterior knowledge ofO,D, andr.

Hsu et al.[29], on the other hand, propose to choose the parameter∊based on an economic perspective.The idea behind their work is based on the observation that a normal user has a fnancial incentive to contribute sensitive information (if the third party or even attacker provide the fnancial compensation).Their economics-inspired solution [29] can calculate an proper∊by striking a balance between the accuracy of the released data and∊.In addition, Naldi et al.[30]calculated the parameter∊according to estimation theory.More specifcally, Naldi et al.put their emphasis only on the counting query (as the counting query leads to the minimal sensitivity) and defne their RoD.Their solution is similar to the solution in this paper.Nonetheless, the restriction on the counting query implies the limited practicality.Tsou et al.[31] also presented an RoD and their RoD is defned by restricting the confdence level of the magnitude of Laplace noise.With an observation that the data owner who wants to evaluate the RoD is only in possession of an original datasetOand a candidate differentially private synthetic datasetD.With another observation that the magnitude of Laplace noise can be bounded with high probability, the value range of the Laplace noise can then be estimated with a certain confdence level.As a result, the estimated value range of the Laplace noise can be used to determine the level of distortion for the record values, and this also implies the privacy level.

1.2 Problem Statement

The assessment of the RoD and data utility of the DP synthetic dataset presents the following two diffculties.

• RoD requires good explainability for layman users in terms of a privacy guarantee, while simultaneously allowing quantitative interpretation to enable the privacy effect of different DPDR algorithms to be compared.In particular, although the privacy budget∊in DP has a mathematical explanation, it is diffcult for layman users to comprehend the meaning behind the defnition.Moreover, the privacy budget is inconsistent with the requirements in the current privacy regulations such as GDPR and CCPA, because the relation between∊and legal terms such as “single-out” remains to be investigated.

• Usually, it is necessary to generate a synthetic dataset and then estimate the corresponding privacy level by calculating the RoD.Nonetheless, this process requires an uncertain number of iterative steps until the pre-defned privacy level is reached, leading to ineffciency in synthetic dataset generation.Thus, the aim is to develop a solution that can effciently estimate the privacy level of the DP synthetic dataset.

Though the methods in Section 1.1 can be used to determine∊(or to quantify the privacy level), all of them have inherent limitations as mentioned previously.In particular, two of these studies [28,29] can apply only in the case of interactive DP, where the data analyst keeps interacting with the server and receives query results from the server.Nevertheless, as interactive DP suffers from the privacy budget completion problem, the DPDR in this paper only considers non-interactive DP (see Section 2.1), which results in the publication of the differentially privacy dataset allowing an arbitrary number of queries.Thus, the studies [28,29] are not applicable to the assessment of RoD.Moreover, though the method in [30] is somewhat related to non-interactive DP, its application is limited to the counting queries.Sarathy et al.[32] also have a similar limitation since their work only applies to numerical data.Lastly, Tsou et al.[31] method works only when the synthetic dataset is synthesized with the injection of Laplacian noise.Unfortunately,this is not always the case, because Laplacian noise leads to synthetic dataset with awful utility and therefore the data owner might choose alternatives.The design of PriBayes, JTree, Priview,and DPSynthesizer (in Section 1.1.1) similarly indicate that a more sophisticated design is used for DPDR, further limiting the applicability of this work [31].

1.3 Contribution

Our work makes the following two contributions:

• We defne a notion for evaluating the risk of disclosure (RoD) particularly for the DP synthetic dataset.The state-of-the-art DPDR algorithms decouple the original dataset from the synthetic dataset which makes it diffcult to evaluate the RoD.However, we strive to quantify the RoD without making unrealistic assumptions.

• We propose a framework for effciently determining the privacy budget∊in DP, using the curve ftting approach, taking into consideration the desired trade-off between the data utility and privacy.

2 Preliminaries

2.1 Differential Privacy(DP)

The scenario in our consideration is a trusted data owner with a statistical database.The database stores a sensitive dataset.The database constructs and publishes a differentially private synthetic dataset for the public.In this sense, DP has been a de facto standard for protecting not only the privacy in the interactive (statistical database) query framework but also the (noninteractive) data release framework (see below).

There are two different kinds of DP scenarios, interactive and non-interactive.In the former,a dedicated and trusted server is located between the data analyst, who issues queries to the server(the data owner), and server (data owner).The server is responsible for answering the queries issued by data analyst.However, to avoid information leakage from query results, before forwarding the query result, the server will perturb it.Obviously, the interactive setting is cumbersome because in reality the data owner needs to setup a dedicated server.On the contrary, in the latter,the server (data owner) simply releases a privatized dataset to the public after the sanitization of dataset.During the whole process, no further interaction with anyone is needed.The synthetic dataset approach is a representative for non-interactive DP.Throughout the paper, we consider the non-interactive setting of DP (i.e., DPDR) unless stated otherwise.

Let∊andMbe a positive real number and a randomized algorithm with the dataset as the input, respectively.We claim thatMis∊-DP if, for all neighboring datasetsD1andD2that differ at most one single record (e.g., the data of one person), and all subsetsSof the image ofM,

where the parameter∊can be adjusted according to the tradeoff between utility and privacy;a higher∊implies lower privacy.Therefore,∊is also called theprivacy budgetbecause, the number of query responses is positively proportional the privacy loss.From the above defnition, we can also know that DP provides a cryptographic privacy guarantee (from indistinguishability point of view) that the presence or absence of a specifc record will not affect the algorithm signifcantly.From attacker’s point of view, (s)he cannot tell whether a specifc record exists given the access of the algorithm output.

DP can be achieved by injecting a zero-mean Laplace noise [33].Specifcally, the noise sampled from a zero-mean Laplace distribution is added to perturb the query answer.Then, the data analyst only receives the noisy query answer.With two parameters on the mean and variance,Laplace distribution is determined jointly by∊and global sensitivity,

of the query functionq; that is, for any queryqand mechanismM,

is∊-DP, whereLapis a random variable that follows a zero-mean Laplace distribution.Apparently, as stated above,∊determines the tradeoff between privacy and data utility.DP features the sequential composition theorem, which states that by querying the datasetktimes,if each noisy response satisfes∊-DP, then all thekqueries achievek∊-DP together.In addition,DP involves post-processing, which states that any kind of data-independent processing of a noisy answer (∊-DP) does not compromise its privacy guarantee.

2.2 Voronoi Diagram

In our proposed algorithm in Section 3.2.3, we take advantage of the Voronoi Diagram, a mathematical concept which refers to partitioning a plane into adjacent regions called Voronoi cells to cover a fnite set of points [34].The defnition of a Voronoi diagram is as follows [34,35]:LetXbe a set ofnpoints (called sites or generators) in the plane.For two distinct pointsx,y∈Xthe Voronoi region/cell associated toxis the set of all points inthe planethat are closer toxthan to any other point in the plane (i.e.the nearest neighbor to the point).In other words,the region associated toxis all the points in the plane lying in all of the dominances ofy,i.e.,region(x)=dominance(x,y), wheredominance(x,y)={p∈R2|l2(p,x)≤l2(p,y)},wherel2is the Euclidean distance.Due to specifc geometrical structure of Voronoi diagrams and their simplicity in visual perception, they have been used by several research studies, such as fle searching, scheduling and clustering [34].Recently, the Voronoi diagram has also been used for preserving location privacy in various research studies [36–38].In [36] the authors propose a privacy preserving model for mobile crowd computing to hide users in a cloaked area based on the Voronoi diagram.This paper takes advantage of the Voronoi diagram to provide k-anonymity for users in each Voronoi cell.In another study, Bi et al [38] combine local differential privacy and Voronoi diagram in order to preserve privacy in edge computing.

Compared to the state-of-the-art, in this paper we adopt Voronoi diagram in a completely different manner for evaluating the RoD in a differentially private synthetic dataset.

3 Proposed Approach for Evaluating Risk of Disclosure

In the following, we consider the setting of an original datasetOand the corresponding differentially private synthetic datasetD, both sizedm×nand with numeric attributesA1,A2,...,An.Each record inOrepresents personal information; a concrete example ofOis a medical dataset,where each record corresponds to the diagnosis of a patient.We do not assume a particular DPDR algorithm unless stated otherwise.The DPDR algorithms in Section 1.1.1 are all available for consideration.Our goal is to develop friendly notions of both RoD and utility, ensuring that these notions can easily quantify the RoD and utility ofD, given the access toOand the satisfaction of∊-DP.

First, we discuss a simple metric for RoD in Section 3.1.In Section 3.2, we present four privacy notions.After that, we claim that the combined notion would be the best by justifying its self-explainability.Thereafter, we present our solution of how to quickly evaluate the utility of the synthetic dataset, given a specifc privacy level, in Section 3.3.At last, we present in Section 3.4 a unifed framework of calculating the maximal privacy budget∊by jointly considering utility and RoD.

3.1 Straightforward Metric for RoD

Irrespective of the approach that was followed to generate the synthetic dataset, each record inDcould be “fake”; i.e., the existence or non-existence of a record in the synthetic dataset does not indicate the existence status of this record in the original dataset.In theory, even an attacker with abundant background knowledge cannot infer the individual information inO.Specifcally, the privacy foundation lies in the fact thatDis no longer a transformed version ofO, and one cannot linkOandD.Nonetheless, in reality, layman users are still concerned about the probability of the attacker re-identifying an individual from the synthetic dataset.We term this phenomenon the scapegoat effect.In particular, the scapegoat effect states that despite the fact that the information about an individualxinOwill almost certainly not appear inD, because a recordinDcould be suffciently similar toxand the attacker only has partial knowledge ofx, the attacker will(falsely) identifyasx.We claim the importance of the scapegoat effect because this is similar to the skewness attack inl-diversity [14].In other words, an innocent individual might be accused of a crime if they are misclassifed as either being or not being in the dataset.

Considering that most people may be concerned about the probability of an individual being re-identifed by an attacker, given a synthetic dataset, a straightforward method for assessing the privacy level of the synthetic dataset would be to calculate the hitting rate, which is defned as the ratio of the number of overlapping records to the total numbermof records in both datasets.Despite its conceptual simplicity, the use of the hitting rate incurs two problems.

• First, because of the curse of dimensionality, the density of the data points in a highdimensional space is usually low.This could easily result in a very low hitting rate and an overestimated level of privacy guarantee.

• Second, such an assessment metric leads to a trivial algorithm for a zero hitting rate.For example, a synthetic dataset could be constructed by applying a tiny (and non-DP)amount of noise to each record in the original dataset.Owing to the noise, the records in the original and synthetic datasets do not overlap, leading to a zero hitting rate and an overestimated level of privacy.

3.2 Our Proposed Methods for RoD

In this section, we develop friendly privacy notions (or say friendly RoD estimation) from a distance point of view.More specifcally, as we know from the literature, in the DPDR scenario,the original datasetOis already decoupled from the synthetic datasetD.A consequence is that there is no sense to connect betweenOandD.This also implies the diffculty in defning the appropriate RoD.However, the previous work [28–31] sought different ways to create the linkage betweenOandD, as the linkage between them is the most straightforward way for human understanding.Unfortunately, the privacy notion based on the linkage inevitably incurs security faw, especially in the sense that such a linkage does not exist.

In the following, taking the scapegoat effect into consideration, a distance-based framework,(y,p)-coverage, is frst proposed in Section 3.2.1 to minimize the scapegoat effect and to reconcile the privacy level and decoupling ofOandD.The idea behind(y,p)-coverage is inspired by the observation that, even without the knowledge of the linkage betweenOandD, the only strategy left for the attacker is still to seek the closest record inOas the candidate original record inD.However,(y,p)-coverage is not suitable for measuring RoD because it has two parameters and does not have total order (described in more detail at the end of Section 3.2.1).Subsequently, we propose RoD metrics to measure the risk of re-identifcation.

3.2.1 (y,p)-Coverage

Here, we propose the notion of(y,p)-coverage as a framework for evaluating RoD.The idea behind(y,p)-coverage is that, the attacker would exhaustively search for a candidate matched record inO, given access toD.In particular, givenDias theith record ofD(ith row ofD),due to the lack of pre-knowledge, the attacker’s research range would be in the neighborhood of a specifc recordDi.In this sense, the corresponding privacy metric can be formulated as a minimum weight bipartite matching problem in graph theory.Also from graph theory, we know that one can use the Hungarian Algorithm to handle minimum weight bipartite matching problem and so one can conduct the same algorithm to evaluate the RoD with the observation thatOandDwould be of the same size.In particular, Algorithm 1 is the pseudocode of the above idea,whose aim is to test if the distance-based(y,p)-coverage is fulflled.GivenOandD, we construct a complete weighted bipartite graphG=(V,E,W), where

In the graphG, each edge has an edge weight that indicates the dissimilarity between the respective records; hence, the edge weights are defned as

The graphGhas 2mvertices, each of which corresponds to a record fromO.Thus, each vertex can also be seen as ann-dimensional row vector.Under such a construction,Gis completely bipartite as all the vertices fromOare connected to all those fromD.No direct edge for any pair of vertices both of which are forO(andD) exists.We also note that, the notation ‖·‖ denotes the norm.Here, while many norms can be used, an implicit assumption in this paper is that we always choose to use the Euclidean distance for ‖Oi−Dj‖=‖(χ1,...,χn)‖ for certainχ1,...,χn.However, the other norm can also be used as an alternative.

Given a matchingM, let its incidence vector bex, wherexij=1 if(i,j)∈Mand 0 otherwise,and the perfect matching of the minimum weight is a subset of edge weights such that

wherecij=wij.Once the Hungarian algorithm is performed, we can derive the perfect matching and the corresponding edge weightω, whereωis anm-dimensional vector and theith entry ofωdenotes an edge weight of the minimum weighted bipartite matching forDi.We then calculate the number of weights less than or equal toyas a countζ,

whereIωi≤ydenotes an indicator function withIωi≤y=1 in the case ofωi≤y, andIωi≤y=0 otherwise, given a user-defned weighty.Subsequently, we calculatep′=ζ/m.With the probabilitypfrom the user,Dis supposed to fulfll(y,p)-coverage ifp′≤p.

Algorithm 1: (y,p)-coverage Input:User-defned weight: y Input:User-defned probability: p Input:Original dataset: O Input:DP synthetic dataset: D Output:(Yes/No) Whether D fuflls (y,p)-coverage 1: M ←HUNGARIAN ALGORITHM(O,D);2: ξ =∑mi=1 Iωi≤y;3: p′=ζ/m 4:return (p′≤p) ? fulflled:not fulflled;

Despite its conceptual simplicity and theoretical foundation,(y,p)-coverage cannot be used for assessing RoD because(y,p)-coverage has two parametersyandpand does not have total order.Note that the purpose of developing the RoD metric is to enable layman users to conveniently choose the privacy budget∊in DP.However, when the notion of(y,p)-coverage is used,it may be diffcult to determine which of, for example,(3,0.5)-coverage and(4,0.4)-coverage,improves the privacy.Hence, the following sections defne additional privacy notions with total order to enable an RoD comparison.

3.2.2 y-Privacy

An underlying assumption for the(y,p)-coverage that the attacker conducts a search to look for a bijective matching betweenOandDby using the Hungarian algorithm.However,this assumption may fail in reality.To ft the reality setting, one can relax such an assumption,ensuring that the attacker instead performs an exhaustive search to fnd a matching betweenOandD.In this process, two records inDmay happen to be matched against the same record inO.In(y,p)-coverage, we only keep one matching and get rid of another matching, which does not make sense.Therefore, in this section, we propose to usey-privacy to overcome the above limitation.While(y,p)-coverage can be seen as an average-case analysis,y-privacy is featured by its focuses on the worst-case analysis.

Algorithm 2 is proposed to achievey-privacy; more specifcally, it is used for verifying whether a given dataset satisfesy-privacy.In what follows, we consider the case ofn=1 with integral values inOto ease the representation.We will relax this assumption later.However, our implementation is a bit different from the above description.Instead, we in Algorithm 2 turn our focus to fnding the mapping, instead of the matching, betweenOandDwith the minimum incurred noise.First, we fnd the minimum valuefor each recordDiinDsuch that [Di±contains one original record inO.This ensures that an original record is within the attacker’s search range.Then, for eachiny′, we calculate

The above equation indicates that, becauseycan be seen as all of the possibilities, when the attacker sees a record, it needs to be verifed whether this was a brute-force guess.Consequently,a loweryimplies a downgrade privacy.Thus, Eq.(8) can also be seen as the probability that the attacker successfully makes a correct guess on an original record inOwithin the range[Di−y,Di+y], given that a recordDi∈Dis always at most 1/(2y+1).One can also choosey′in such a way that the median ofy′is selected asyto strike a balance between the privacy and utility.In comparison, the choice ofy′goes back to the average-case analysis, and choosing the minimumy′asyhas a similar favor of(y,p)-coverage.

?

One can see that Algorithm 2 can also apply to the case ofn≥2, once we properly defne the operation [Di±, becauseDiisn-dimensional.The defnition can be derived by considering‖Di−x‖≤yfor alln-dimensional vectorsx.The same patch can be used in the operation [Di±even if the record values are foating numbers.

Under the framework of(y,p)-coverage,y-privacy considers a general attack strategy and provides a worst-case guarantee.Compared to(y,p)-coverage,y-privacy has total order, and it is easy to see thaty-privacy is better thany′-privacy wheny≥y′in terms of the privacy guarantee.Intuitively, the above argument thaty-privacy is better thany′-privacy wheny≥y′also indicates that each record in the synthetic dataset satisfyingy-privacy will be at leasty-far away from the closest record in the original dataset, in contrast to the synthetic dataset, which satisfesy′-privacy.However,y-privacy is still not practical when adense dataset(consisting of a huge number of records) is considered.Specifcally, the common weakness ofy-privacy and(y,p)-coverage is that when the records in a dataset are seriously dense, the parameteryiny-privacy and(y,p)-coverage should be very small.This can be understood by the fact that the records are close to each other both before and after the noise injection.It turns out that the parameterybecomes less meaningful as a privacy level.

3.2.3 Voronoi Privacy

The notion ofy-privacy can also be generalized to consider its extreme condition.In other words, becausey-privacy considers ay-radius ball centered at each data point and considers the number of data points inOcovered by thisy-radius ball, we can follow this perspective and consider they-radius balls centered at all data points inO.The rationale behind the above consideration is to determine the arrangement of the dataset with the optimaly-privacy.Expanding the radius of ally-radius balls ultimately leads to a Voronoi diagram [39].As explained in Section 2.2,this diagram is a partition of a multi-dimensional space into regions close to each of a given set of data points.Note that a Voronoi diagram can be effciently constructed for two-dimensional data points, but for high-dimensional data points this would only be possible by using approximation algorithms [40,41].The Voronoi diagram is characterized by the fact that, for each data point, a corresponding region consisting of all points of the multi-dimensional space exists closer to that data point than to any other.In other words, all positions within a Voronoi cell are more inclined to be classifed as a particular data point.

From the perspective of RoD, we then have an interpretation that, in terms ofy-privacy,each record inDcannot be located at these positions within the Voronoi cell; otherwise, an attacker who fnds such a record inDis more inclined to link to a particular record inO.The above argument lies in the theoretical foundation of Voronoi privacy.Algorithm 3 shows the calculation of Voronoi privacy, given access toOandD.In particular, the rationale behind Voronoi privacy is to derive the optimal privatized dataset(in terms of privacy) frst, and then calculate the distance betweenDandas an RoD metric.A larger distance implies a higher level of dissimilarity betweenDandand therefore a lower risk of data closure.

?

In this sense, frst, Algorithm 3 constructs an empty datasetThe subsequent procedures gradually add records to, making it optimal in terms of privacy.Then, Algorithm 3 constructs a Voronoi diagram fromObecause the data owner would like to know the corresponding optimal privatized dataset.As mentioned previously, approximation algorithms [40,41] might be candidates for this task.Once the data owner has a Voronoi diagram fromO, the collection of data points on the Voronoi diagram constitutes the optimal privatized dataset.Thus, an infnite number of optimal privatized datasets are available.Here, we aim to fnd the optimal privatized dataset with the optimal data utility.Considering that more perturbation on the record inOimplies lower data utility, for each data point inO, the closest point on Voronoi edges would have been identifed.The data owner collects all these data points asThereafter, the data owner calculates the distance betweenDandas an RoD metric.We particularly mention that different choices of the Distance function are possible in the implementation, depending on the domain of the dataset.In general, thel2distance (Euclidean distance) can be used, whereas the earth mover distance(EMD) could also be used if the data owner was interested in quantitatively measuring the data utility in terms of machine-learning applications.

3.2.4 p-Privacy

Based on the observation that dependency among attributes of the dataset can be a characteristic of the privacy, Algorithm 4 defnes a novel privacy metric, calledp-privacy.This is due to the fact that, in reality, the attacker will not perform a pure random guess; instead, the attacker would make educated guesses according to the distribution ofO.The diffculty for the attacker is that (s)he does possessO.However, becauseDandOhave the similar distribution according to the DPDR, the attacker can still make educated guesses by considering only the distribution ofD.Inspired by this observation, we know that further reducing the futile combinations in the general case ofn≥2 would be necessary.Thus, by computing the correlation among attributes (similar to JTree), our frst step is to construct the dependency graphG.This step would be different from the exhaustive search iny-privacy and(y,p)-coverage.After deriving a dependency graph,we consider each linked part as a clique and obtain a clique setC.We calculateDCi, whereDCiare records with values only for the attributes inCifor each cliqueCiinC.LetUbe the set ofDCi.Then, we produce a candidate tableFwithcombinations by merging eachDCiinUto.The candidate tableFcan be seen as the records that more likely to be the records inO.Subsequently, after a comparison betweenFandO, one can fnd a countξ, where the records ofFbelong toO, and then obtain the attack probabilityp,

?

In the table below, we assume an exemplar original datasetOand synthetic datasetD.Based on this assumption, we show howp-privacy works to serve as a friendly privacy notion.

?

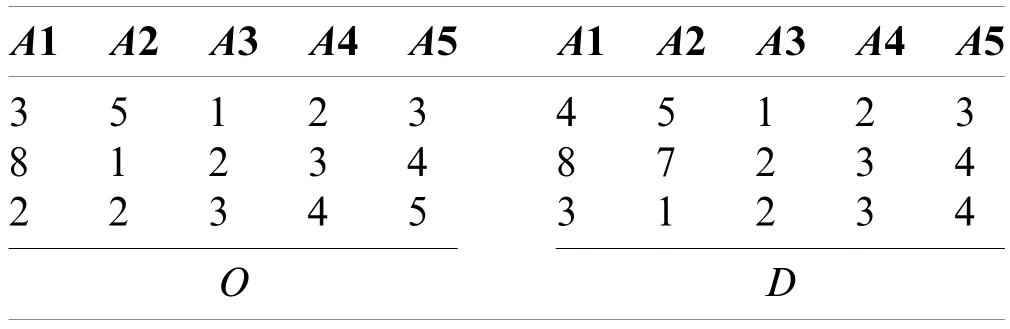
We haveC={A1,A2,(A3,A4,A5)} after the lines 1 and 2 of Algorithm 4.Next, in the line 3 of Algorithm 4, we obtainU={(3,4,8),(1,5,7),[(1,2,3),(2,3,4)]}.In the line 4, we derive the following tableF.

?

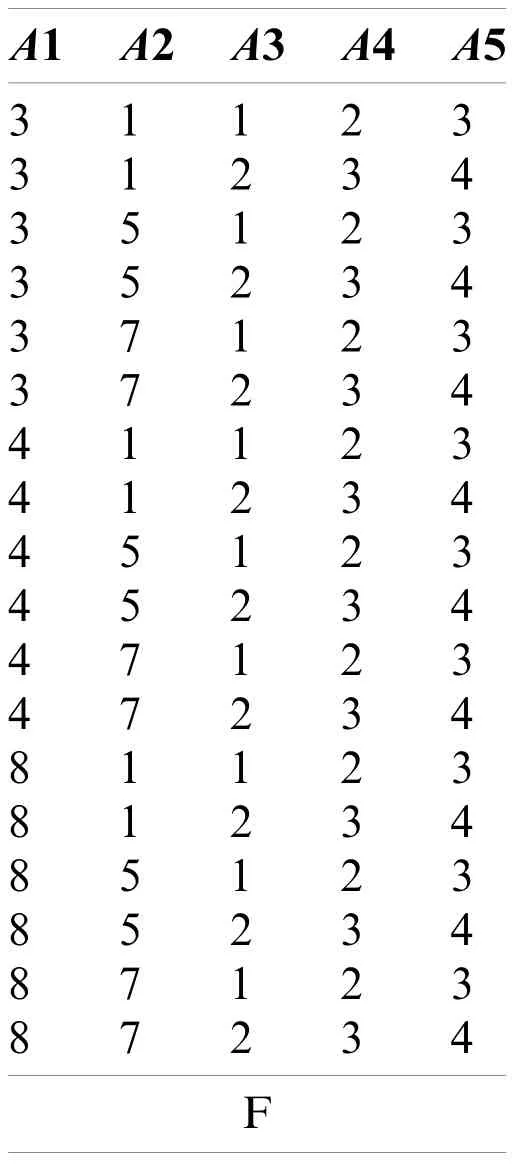
In TableF, both (3, 5, 1, 2, 3) and (8, 1, 2, 3, 4) exist inO.Therefore, in step 5,ξwill be 2.Finally, in the line 6 of Algorithm 4,p=

3.2.5 Data-Driven Approach for Determining ∊

Although how to determine a proper privacy level (notion) is presented in Section 3.2.1～3.2.4,we still eager to develop a method for choosing an proper∊in DP for a given privacy level.In other words, in the previous sections, we only have a friendly explanation on the privacy but still need a concrete method to determine∊.In the following, based on the curve ftting technique, we propose algorithms to obtain satisfactory values for∊.

Baseline Approach for Determining ∊.Inspired by JTree [42], Algorithm 5 adopts a similar strategy from JTree to determine the∊that satisfes the user’s risk and utility requirements.Apparently, if theOis uniformly distributed, only a small amount of noise will be needed to reach the desirable privacy level, because each record has the low sensitivity.However, if the data distribution of the original dataset is not uniform, additional noise is needed to protect the sensitive records, as stated in Section 2.1.

More specifcally, the data owner can determine the sensitive records and the variance of Laplacian noise, given the marginal tables in JTree.Thus, we construct the corresponding dependency graph and calculate the marginal tables.Then, once we have a user-defned probabilitypthat represents the preferable utility and privacy levels, the value of∊can be derived from the equation

The above procedures are similar to those in JTree, except that some operations are ignored.Moreover, as count queries are the fundamental operation that can have minimal impact on the function output, the global sensitivityΔ(f)is 1.So, the 95% confdence interval(μ+2σ)ofis used in our consideration as the maximum value that representsp.This choice enables us to determine a satisfactory∊via Algorithm 5.

?

Unfortunately, Algorithm 5 poses certain problems, such as the possibility that, because different kinds of DP noise injection mechanisms could be used, one cannot expect that the∊retrieved from Algorithm 5 can be suitable for all of DP noise injection mechanisms.On the other hand, as the utility is closely related to∊, the choice of∊is also critical in improving the data utility.This makes it necessary to develop a more accurate method for estimating∊.

Data-Driven Approach for Determining ∊.The simplest idea to determine∊is an iterative algorithm; i.e., we generate a synthetic dataset with a chosen∊and see whether the utility goes to be what we want.This is a theoretically feasible solution but is very ineffcient, especially in the case of an uncertain number of iterations.Therefore, curve ftting, a data-driven approach, is proposed to learn the correlation between privacy level and∊.The curve bridges between privacy and utility.So, once we derive the curve,∊can be calculated instantly, given the desired level of utility.The remaining question is how we can derive the curve.The corresponding privacy levels can indeed be obtained after generating a large number of differentially private synthetic datasets with different∊values.Thereafter, the curve can be learned on the basis of the learned privacy levels.However, when learning the curve, although this process enables the best ftted coeffcients,we still need to determine the type of curve.Initially, we choose exponential and polynomial curves.After that, we also choose reciprocal curves as an alternative.

One can see from Fig.1 that the reciprocal curve of degree 2 results in the best ft.The predictions in Tab.1 are quite close to the real risk distances.

3.3 Evaluating Utility

3.3.1 Baseline Method for Evaluating Utility

As mentioned in the previous sections, even though the synthetic dataset has already achieved the required privacy level, usually the data utility will be sacrifced.So, the objective of data owner is to maximize the data utility subject to the required privacy.Deriving an explicit formulation for privacy and utility is complex; instead, we resort to data-driven approach.A simple idea for deriving the utility is to iteratively generate different synthetic datasets and then determine the corresponding utility.This operation is very time-consuming.In the worst case, one needs an infnite amount of time to try an infnite number of combinations of parameters.As a result, an algorithm capable of effciently learning the utility of a given synthetic dataset is desired.

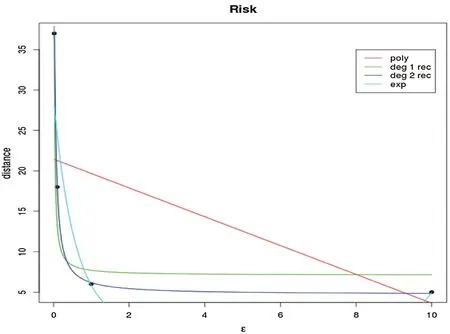
Figure 1:Curve ftting for RoD estimation

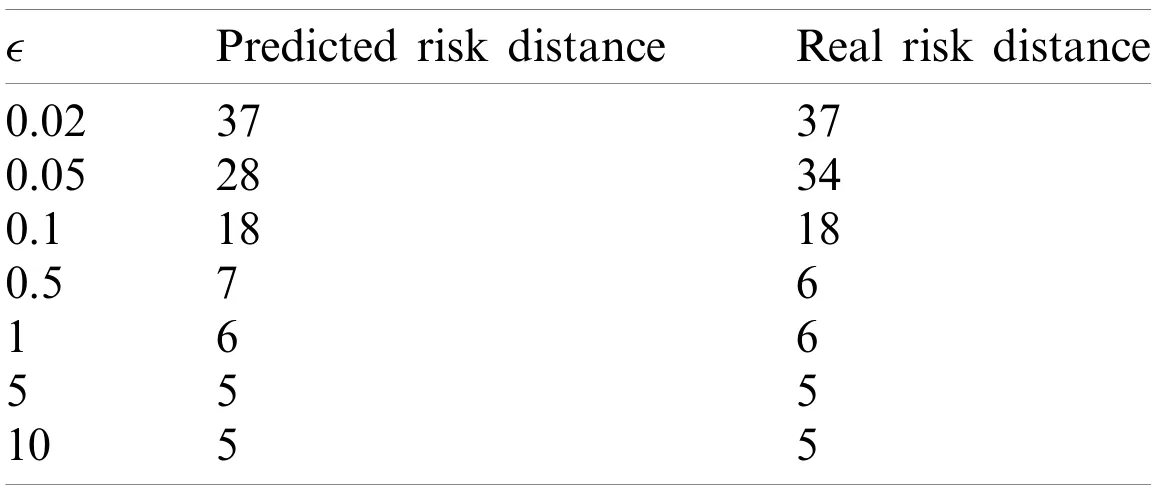
Table 1:Predicted RoD and the real RoD

The statistics such as the mean, standard deviation, and variance can be seen as the most popular statistics used by the data analysts and so the metrics for evaluating data utility.In what follows, for fair comparison, after the use of synthetic datasetD, we also used these metrics to estimate the error of the result.The error of variance introduced by the synthetic datasetDcan be formulated as

As a whole, to evaluate the variance error of the entire dataset, what we can do is to sum up the errors for each record,

Obviously, when the synthetic dataset has smaller estimation error, it also leads to better data utility.The analysis of other statistical measures is also consistent to the ones derived from the above formulas.As a result, we used these statistical measures because of the following two reasons.First, it is because of their popularity and simplicity.Second, we can also learn an approximate distribution from these measurements.Moreover, when there are huge errors for these simple statistics, it would defnitely lead to catastrophic utility loss for the other complex statistical measures.

3.3.2 Data-Driven Method for Evaluating Utility

Usually, calculating the estimation error from the synthetic dataset is to calculate Eqs.(11)and (12) over the differentially private synthetic datasets with∊={0.01,0.1,1,10} is the most straightforward method that we start to try.For example, Fig.2 where the input dataset is a 5×1e6 health dataset with fve attributes HEIGHT, WEIGHT, BMI, DBP, SBP1DBP is diastolic blood pressure and SBP is systolic blood pressure.The height and weight are generated by sampling from a normal distribution manually.Meanwhile,the BMI is calculated from the height and weight.Eventually,DBP and SBP are generated from BMI with some noise with small magnitude.shows the errors incurred by different settings of∊.

Iterating the above process of choosing a∊, generating a synthetic dataset, and then calculating the utility would be highly ineffcient.This is due to the fact that the data owner might want to further improve the utility of the current version of the synthetic dataset.Thus, the data owner will iterate the above process again and again until a satisfactory version appears.As a whole, we decided to generate synthetic datasets for pre-determined∊, and then estimate their errors only.After that, our plan is to use these information to ft a curve bridging the privacy and utility.In particular, we propose using a curve ftting, a data-driven approach, as a surrogate method to learn the correlation between∊and utility measures such as the error of the mean, standard deviation, and variance.Once we have such a curve from curve ftting, we can indeed calculate∊very quickly, given the desired level of utility or vice versa.

Specifcally, in the case of∊var,∊varcan be obtained after generating a large number of synthetic datasets with different values of∊.Thereafter, the curve could be learned using the obtained values of∊var.

However, when performing curve ftting, although this could be used to learn the coeffcients that best ft the chosen curve, one factor that we can have freedom to choose is the type of curve.Initially, the two intuitive choices are exponential and polynomial.A more counterintuitive one would be reciprocal curves.We, however, found that the reciprocal curve with the following form:

In fact, Eq.(14) has room to be improved so as to offer better prediction results.In our consideration, we aim to calculate the errors in the cases of∊= {0.01,0.05,0.1,0.5,1,5,10}.Nevertheless, only three errors are calculated for the cases of∊={0.01,0.5,10}.Afterwards, we learn the curve based on these three errors.These results are shown in Fig.4, where the real statistics and predicted statistics in Tab.2 are matched almost perfectly.

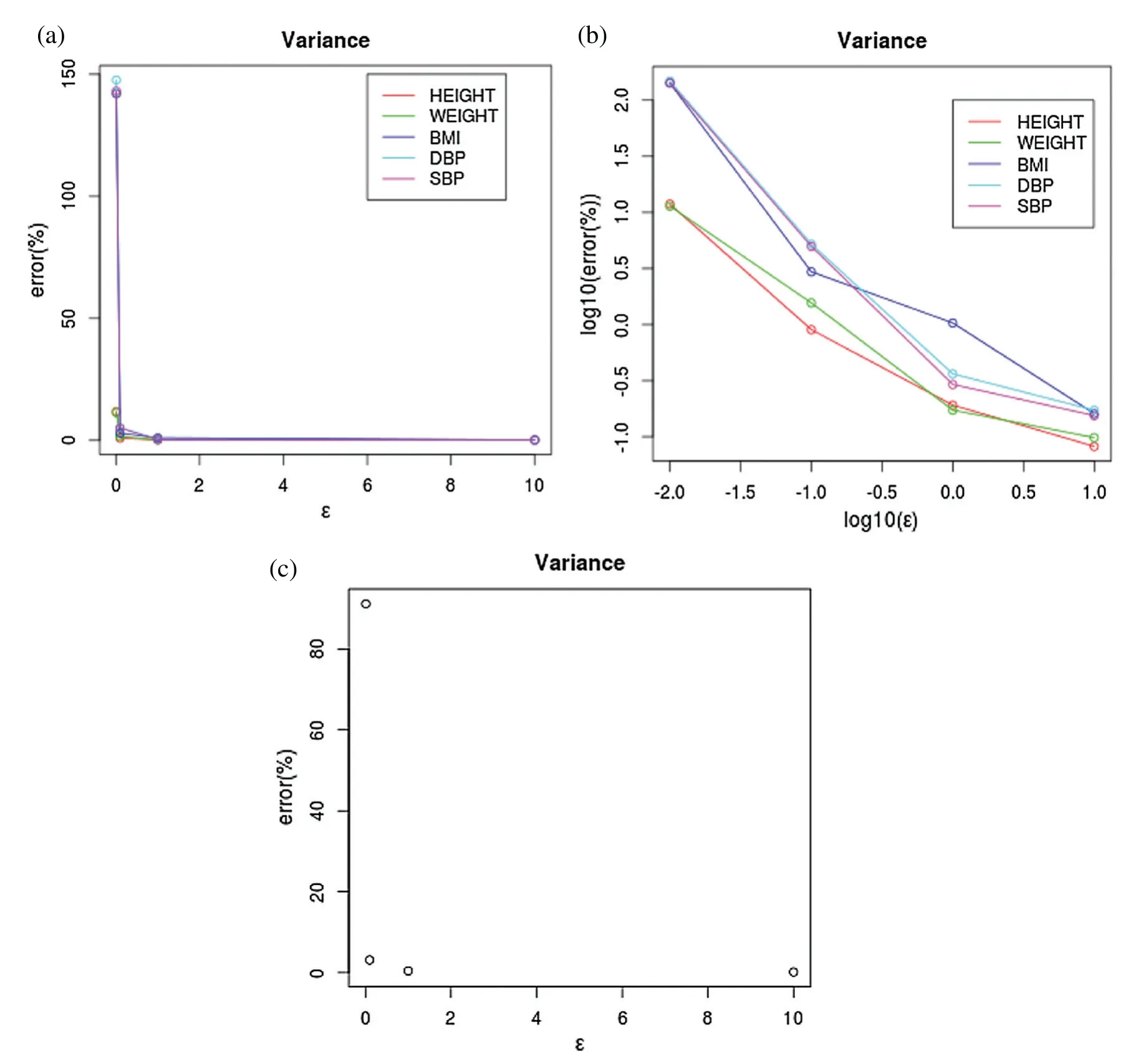
Figure 2:Different methods for the analysis of the error of variance.(a) Each attribute, (b) Log10,(c) average

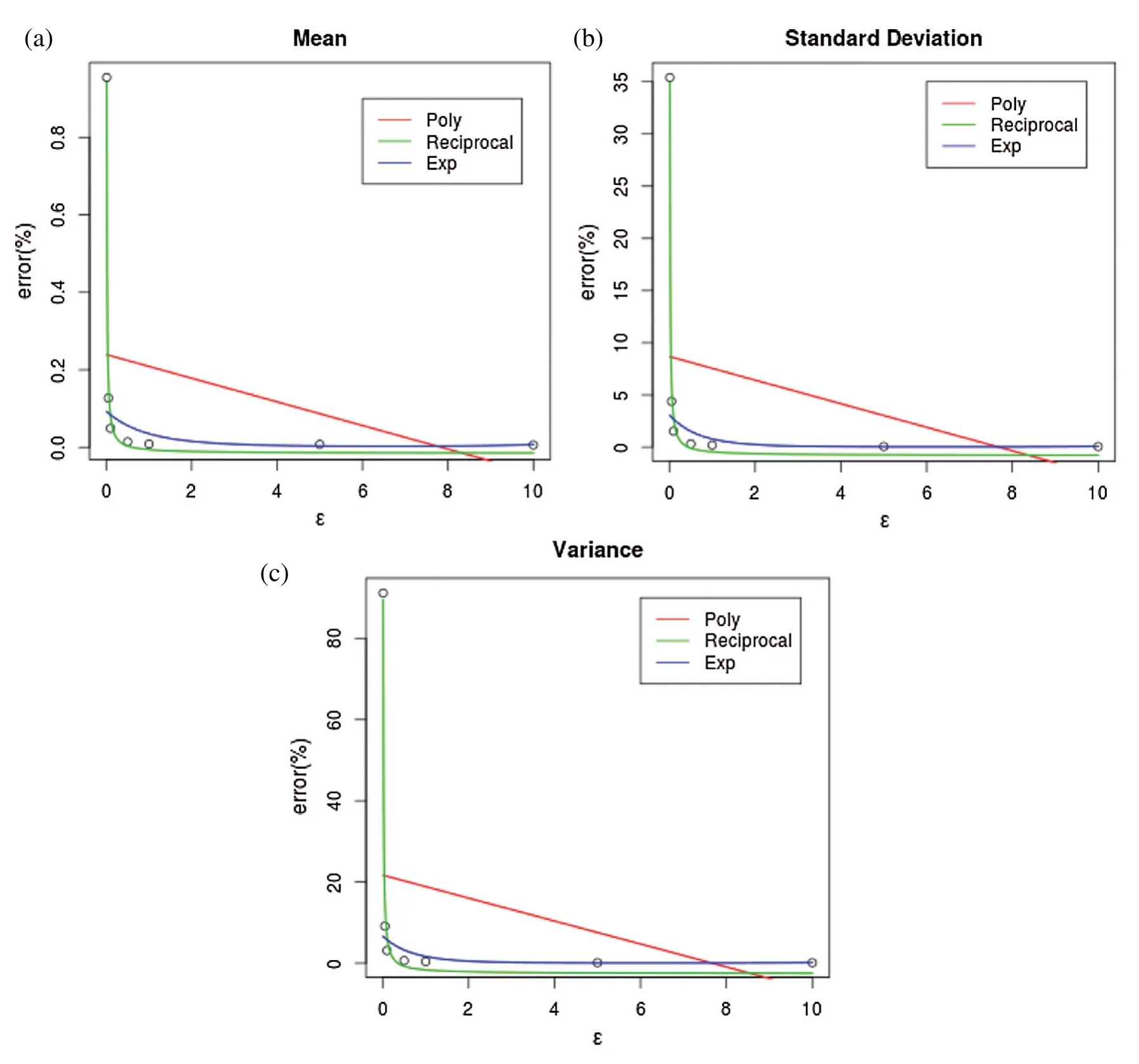
Figure 3:Curve prediction for statistical measures including mean, standard deviation, and variance.(a) Mean (b) standard deviation (c) variance

Despite the seemingly satisfactory results in Fig.4, once we scrutinize Tab.2, we will fnd that there are negative predicted values of∊={5,10}, and this result is not pleasing.Once fxing the shape of the curve ftting and reciprocal curve, we found that the main reason for predictability degradation of the ftted curve can be attributed to the insuffcient degree of the reciprocal (or the other used) curve.Consequently, when we slightly increase the degree of the reciprocal curve,we obtain

Here, after the comparison among the results in both Tab.3 and Fig.5, one can know immediately that the predicted errors are matched against the real error values, with a curve newly learned from the data.

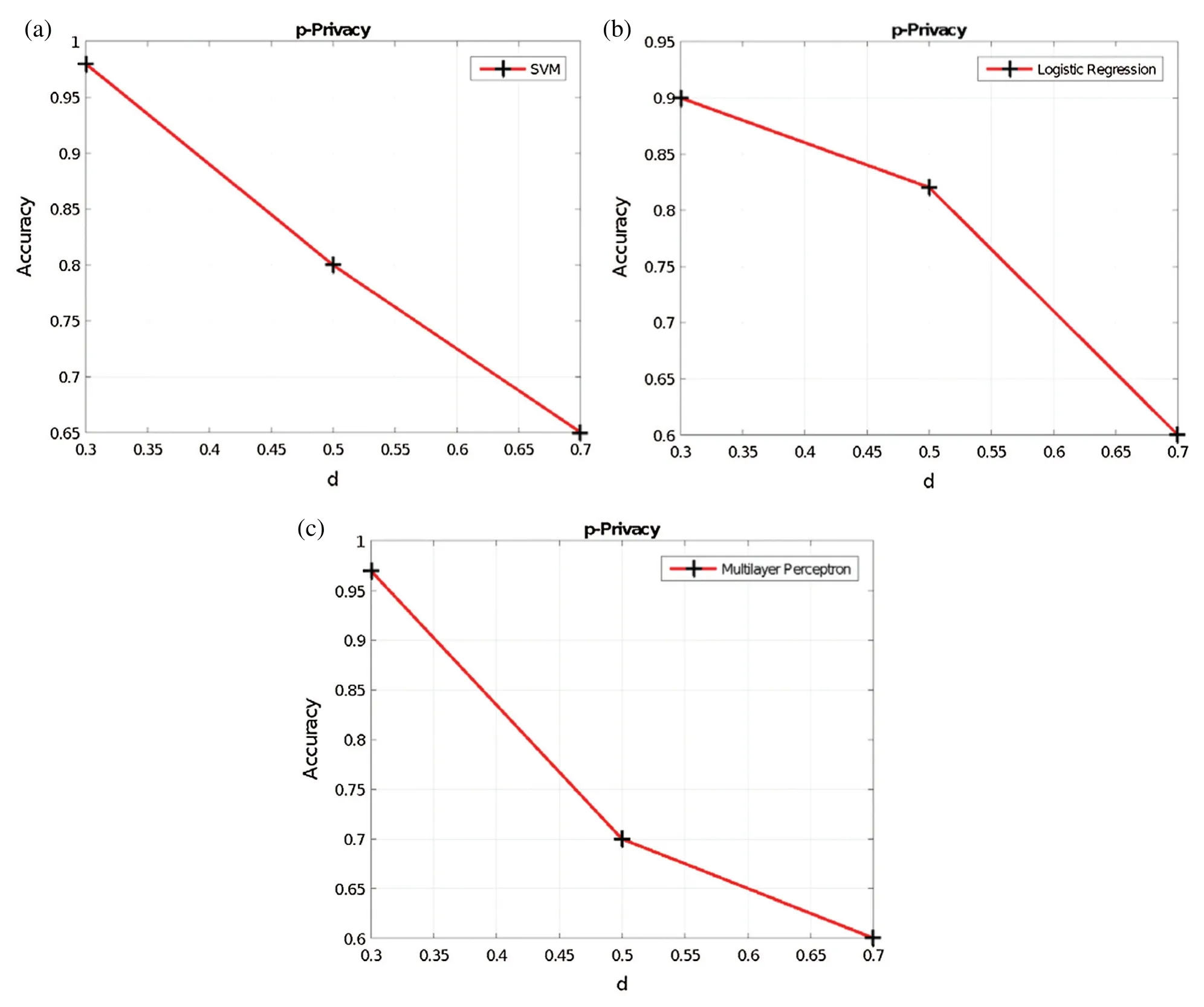
Figure 4:Curve prediction for statistical measures including mean, standard deviation, and variance.(a) Mean (b) Standard deviation (c) variance

Table 2:Comparison between the predicted and real variance errors

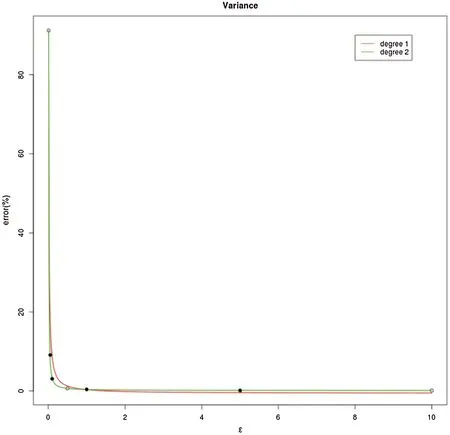
Figure 5:Difference between ftted reciprocal curves with the degree 1 and 2

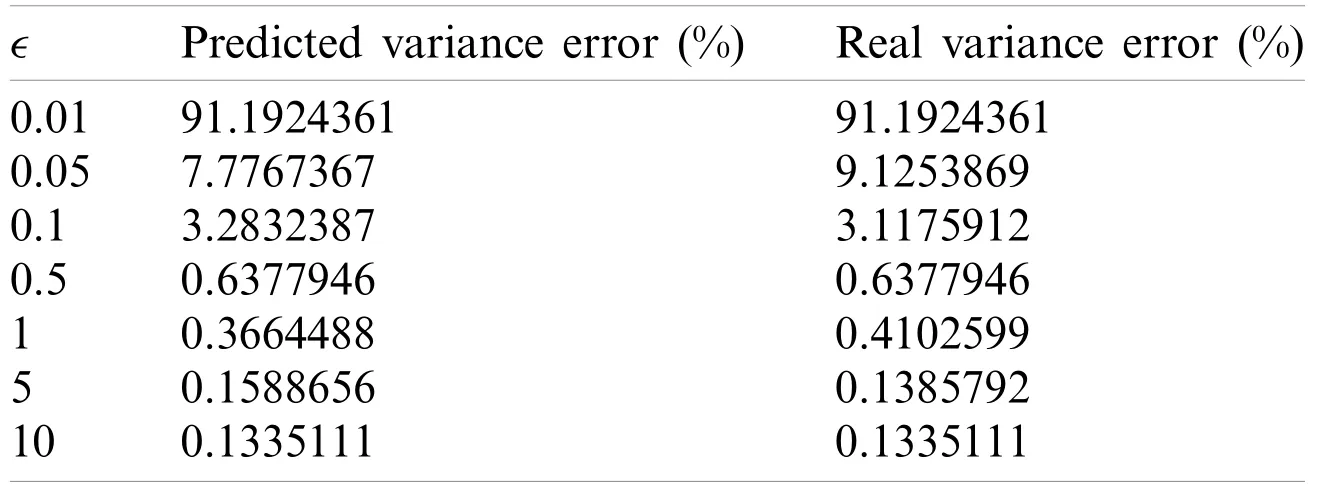
Table 3:Comparison of the predicted and real variance errors after applying Eq.(15)

3.4 Jointly Evaluating RoD and Utility

The data utility results when varyingdin the Voronoi privacy,yin they-privacy, andpin thep-privacy, are provided in Figs.6–8, respectively.Obviously, as the RoD increases, the data utility is not maintained.This is because additional perturbation is added to the original dataset and therefore the synthetic dataset is generated from a data distribution with more noise.

Figure 6:Voronoi privacy vs.accuracy (a) SVM (b) LR (c) MLP

One can know that the extension from the aforementioned data-driven approaches for evaluating both the utility and RoD to a data-driven approach for determining the privacy budget∊with a joint consideration of the utility and RoD can be easily achieved.In essence, from Sections 3.2 and 3.3 we will learn different (reciprocal) curves; one for the privacy level and another for utility.While the curves for the privacy and utility are unrelated at the frst glance, if we consider the DP defnition and the way of how to achieve DP, they, in fact, are correlated to each other.In this sense, multidimensional curve ftting will be an alternative for a more complex setting; i.e., it would be a candidate to be used over the curves learned from Sections 3.2 and 3.3 so as to learn a higher dimensional curve for the privacy level and utility.Since the resulting higher dimensional curve will have a parameter∊, after a simple calculation when the other parameters are fxed, the privacy budget∊can be determined with a joint consideration of the utility and RoD.

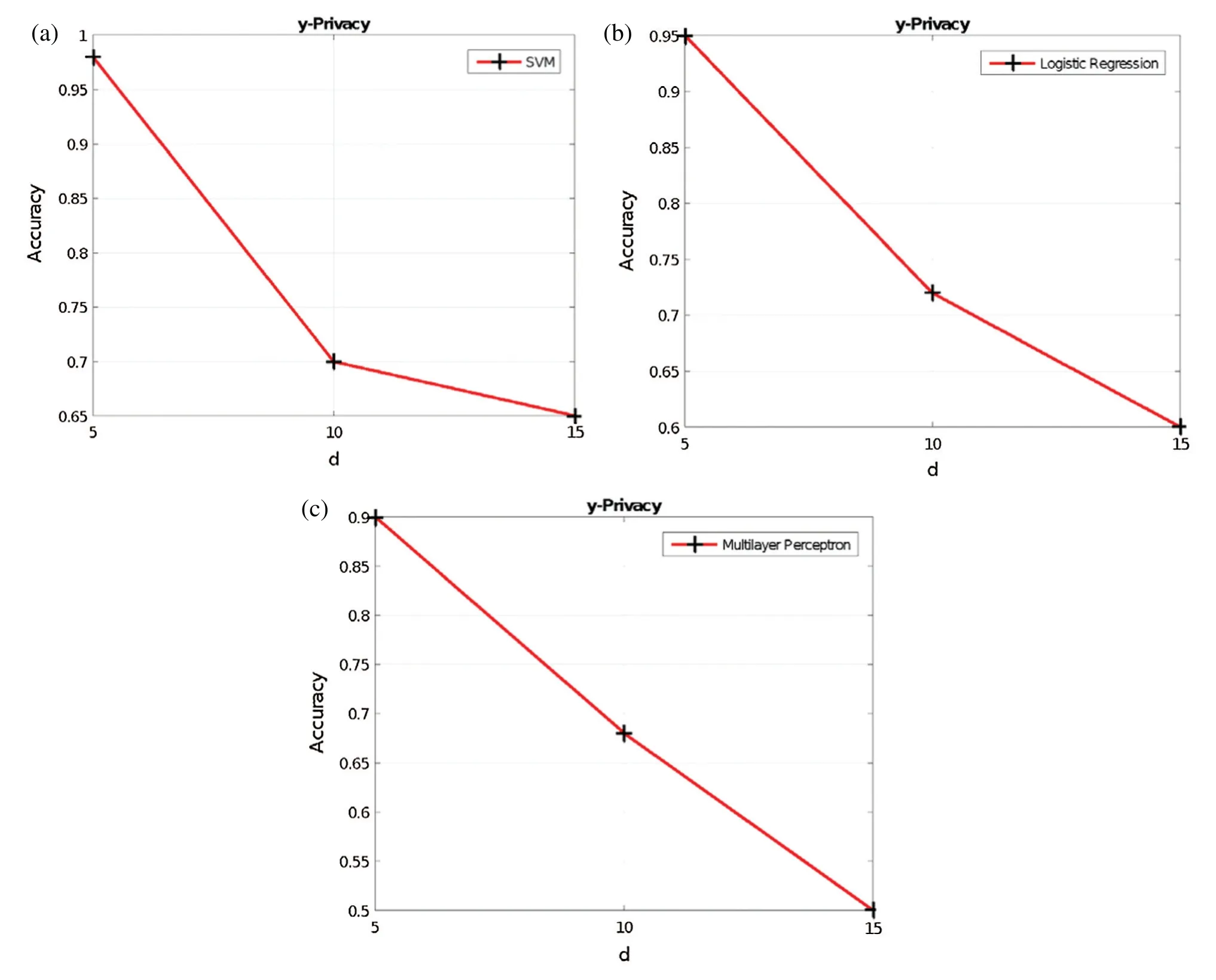
Figure 7: y-privacy vs.accuracy (a) SVM (b) LR (c) MLP

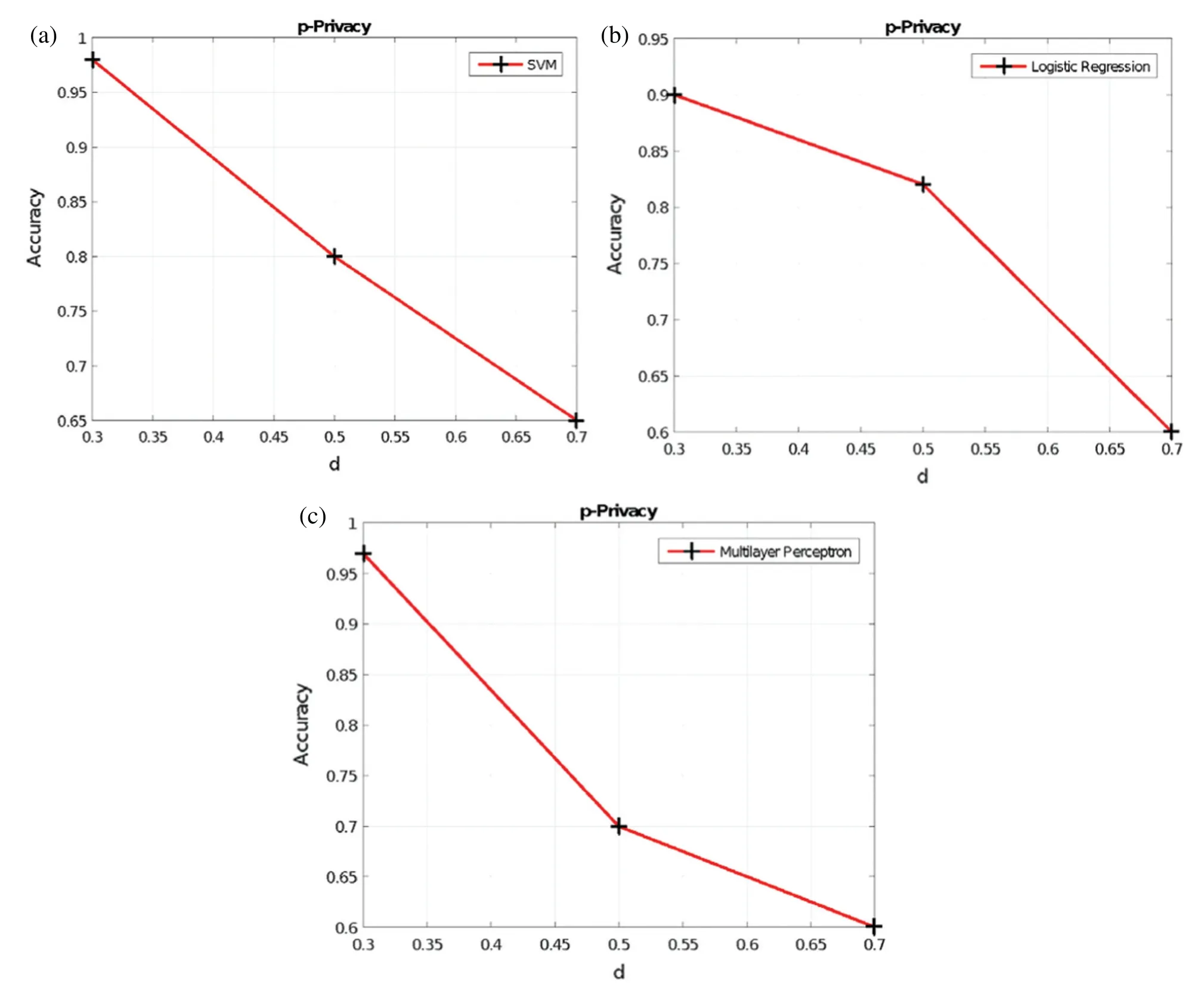
Figure 8: p-privacy vs.accuracy (a) SVM (b) LR (c) MLP

4 Conclusion

In this paper, we proposed a number of friendly privacy notions to measure the RoD.We also developed curve ftting-based approach to determine the privacy budget∊in a data-driven manner with the joint consideration of the RoD and utility.This approach enables novice users to grab the idea behind the level of privacy protection and the data utility.As a result, these users would be able to determine an appropriate privacy budget∊for DPDR, depending on the amount of privacy risk they would be prepared to tolerate and the desired utility.

Funding Statement:The work of Chia-Mu Yu has been initiated within the project MOST 110-2636-E-009-018 of Ministry of Science and Technology, Taiwan https://www.most.gov.tw/.Tooska Dargahi is supported by the UK Royal Society Award (Grant Number IECR3183047,https://royalsociety.org/).

Conficts of Interest:The authors declare that they have no conficts of interest to report regarding the present study.