A New Logarithmic Family of Distributions:Properties and Applications
2021-12-14YanpingWangZhengqiangFengandAlmaspoorZahra
Yanping Wang,Zhengqiang Feng and Almaspoor Zahra
1Central South University Business School,Changsha,China
2Hunan International Business Vocational College,Changsha,China
3Department of Statistics,Yazd University,Yazd,Iran
Abstract:In recent years,there has been an increased interest among the researchers to propose new families of distributions to provide the best fit to lifetime data with monotonic(increasing,decreasing,constant)and non-monotonic(unimodal,modified unimodal,bathtub)hazard functions.We further carry this area of research and propose a new family of lifetime distributions called a new logarithmic family via the T-X family approach.For the proposed family,explicit expressions for some mathematical properties along with the estimation of parameters through Maximum likelihood method are discussed.A sub-model,called a new logarithmic Weibull distribution is taken up.The proposed model is very exible and can be used to model data with increasing,decreasing,modified unimodal or bathtub shaped hazard rates.The maximum likelihood estimators of the model parameters are obtained.To assess the behavior of the maximum likelihood estimators,a comprehensive Monte Carlo simulation study has been carried out.Finally,the potentiality of the new model is shown via analyzing two real data sets taken from reliability engineering and biomedical fields.The comparison of the proposed model is made with the other well-known competitors such as(i)the three parameters exponentiated Weibull and Marshall–Olkin Weibull distributions and(ii)a four-parameter beta Weibull distribution.The practical applications show that the proposed model performs much better than the competitive models and can be used as a good candidate model to analyze data in engineering,medical sciences and other related fields.
Keywords:Weibull distribution;moments;order statistic;residual life function;maximum likelihood estimation
1 Introduction
Speaking broadly,statistical distributions are frequently used for modeling real phenomena in many applied areas including engineering,medical sciences,actuarial,environmental studies,economics,finance,and insurance.Among these distributions,the exponential,Rayleigh and Weibull are some of the most useful models used quite effectively in real-life data modeling.Unfortunately,these distributions have a limited range of capability and thus cannot be applied in all situations to get a better description of the phenomena under consideration.For example,the exponential model is often used for real-life data modeling,but its hazard function is only constant.Whereas,the Rayleigh model is another promising model,but it has an increasing hazard function only.However,the Weibull is a more exible model offering the features of both the exponential and Rayleigh distributions and additionally offering data modeling with decreasing hazard function.But,the problem with the Weibull model is that it is not capable of modeling data with non-monotonic hazard function.
To provide an adequate fit to data having non-monotonic hazard function,there is a clear need for the generalized versions of these distributions.This fact motivated the researchers to propose new extended distributions.This has been done either introducing the modified versions of the existing models or introducing new families of distributions to obtain exible model capable of modeling data with nonmonotonic hazard function.
In the recent advances in distribution theory,researchers have shown a deep interest in proposing new methods to expand the family of lifetime distributions.This has been done through many different approaches by introducing new generators.Some of the well-known generators include a new generalized class of distributions[1],McDonald-G(Mc-G)family[2],beta Marshal-Olkin family of distributions[3],Kumaraswamy Marshal-Olkin family[4],log-gamma-G family[5],Weibull-G family of distributions[6],the exponentiated half-logistic family[7],Lomax Generator[8],A New Lifetime Exponential-XFamily[9],New Extended-F Family[10],A Flexible Reduced Logarithmic-XFamily[11],a new extendedfamily of distributions[12],odd generalized exponential-G family[13],Logistic-Xfamily[14],for further detail;see[15].
In this article,a new family of lifetime distributions called a new logarithmic(NL)family of distributions is introduced by adopting the T-Xfamily approach;see[16].The new family is defined by the following cumulative distribution function(cdf)

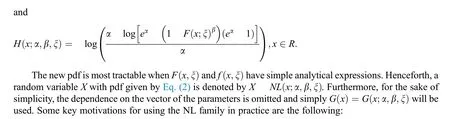
A very simple and convenient method of adding additional parameters to modify the existing distributions.
To improve the characteristics and exibility of the existing distributions.
To introduce the extended version of the baseline distribution having a closed form for cdf,sf as well as hrf.
To provide better fits than the other modified models.
The rest of this article is organized as follows:In Section 2,a special sub-model of the proposed family is discussed.Some mathematical properties are obtained in Section 3.The maximum likelihood estimates of the model parameters are obtained in Section 4.A Monte Carlo simulation study is conducted in Section 5.Section 6 is devoted to analyzing two real-life applications.Finally,concluding remarks are provided in Section 7.
2 Sub-Model Description

For γ=1 and different values of α,β and θ,plots of the pdf of the NLW distribution are sketched in Fig.1.For the selected values of the parameters,some possible shapes for the hrf of the NLW model are shown in Fig.2.
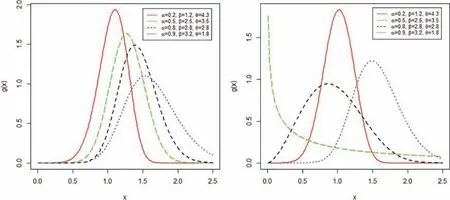
Figure 1:Different plots for the pdf of the NLW distribution
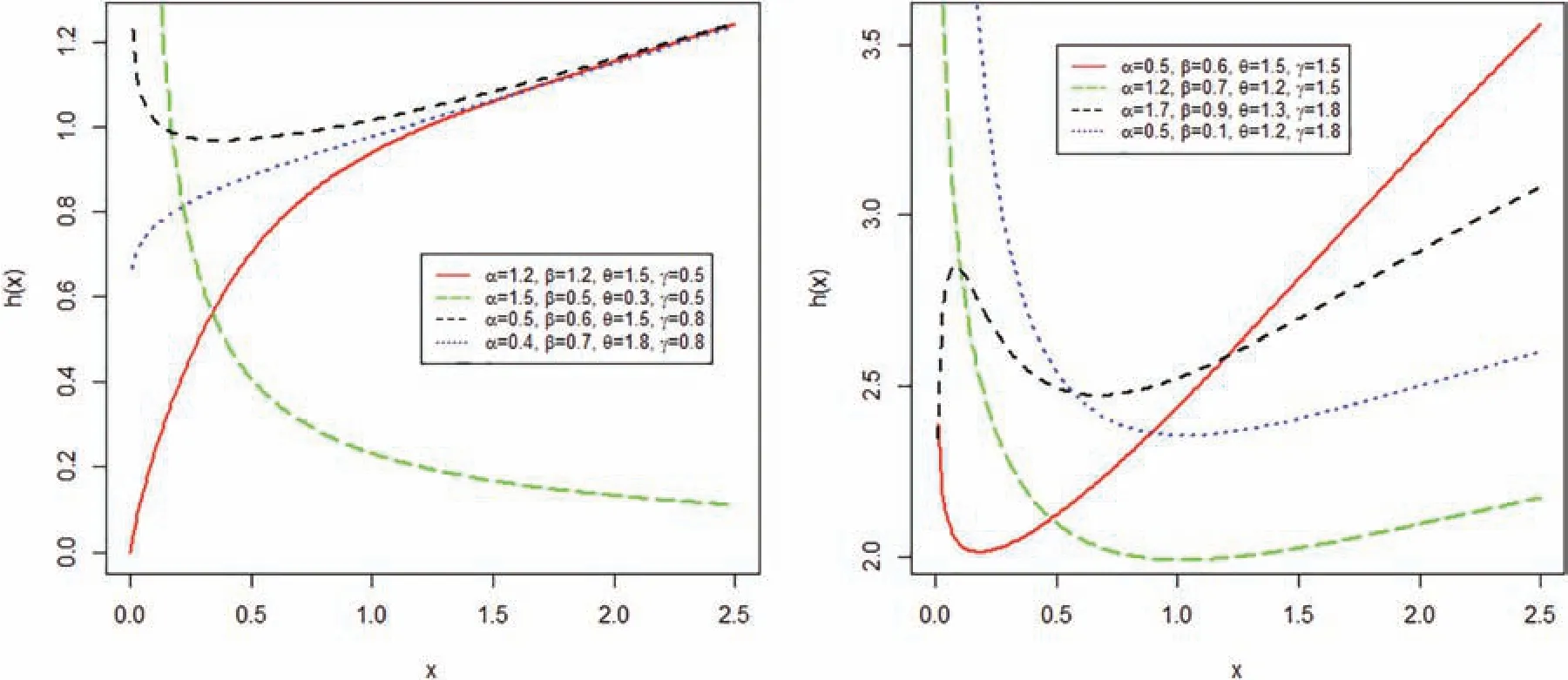
Figure 2:Different plots for the hrf of the NLW distribution
3 Basic Mathematical Properties
In this section,some statistical properties of the proposed family are derived.
3.1 Quantile Function
LetXbe the NL random variable with pdf given by the Eq.(2),the quantile function ofX,sayQ(u)is given by

where,uhas the uniform distribution on the interval(0,1)andG-1(.)is the inverse function ofG(.).From Eq.(5),it is clear that the proposed family has a closed form solution of its quantile function which makes it easier to generate random numbers.
3.2 Moments
Moments are very important and play an essential role in statistical analysis,especially in the applications.It helps to capture the important features and characteristics of the distribution(e.g.,central tendency,dispersion,skewness and kurtosis).Therth moment of the NL family of distributions is given by

Furthermore,a general expression for moment generating function(mgf)of the NL random variableXis
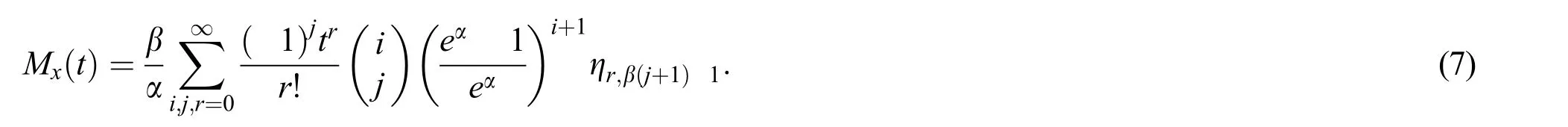
3.3 Residual and Reverse Residual Life
The residual life offers wider applications in reliability theory and risk management.The residual lifetime ofXdenoted by(Rt)is derived as
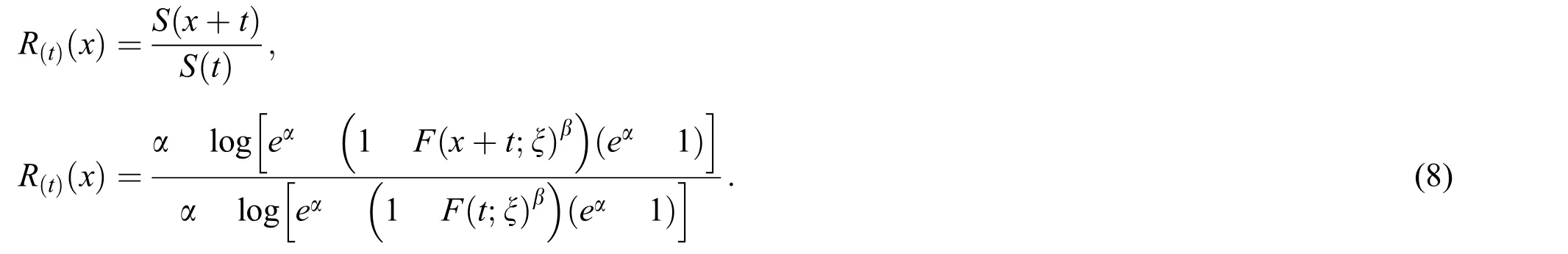
Additionally,the reverse residual life of the NL random variable denoted by (Rt)is
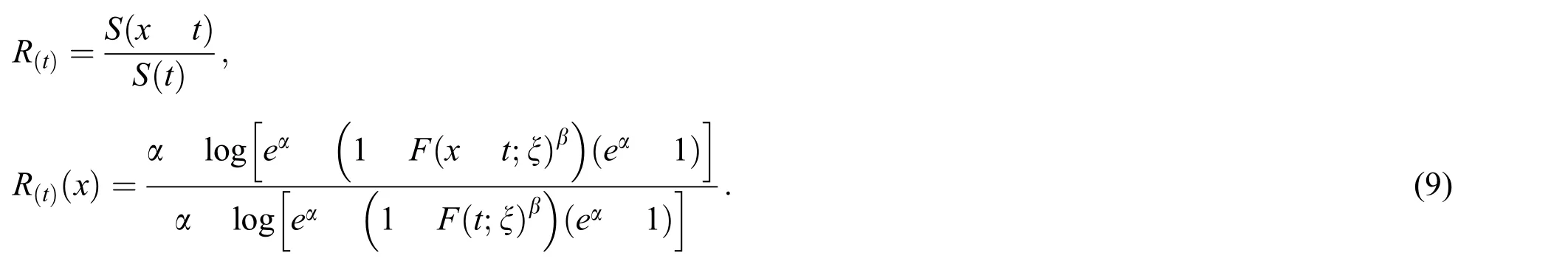
3.4 Order Statistics
Order statistics are among the essential tools in inferential and non-parametric statistics.The applications of these statistics appear in the study of reliability and life testing.LetX1,X2,,Xkbe a random sample of sizektaken independently from the NL distribution with parameters α,β and ξ.LetX1:k,X2:k,,Xk:kbe the corresponding order statistics.Then,the density ofXr:kfor(r=1,2,,k)is given by
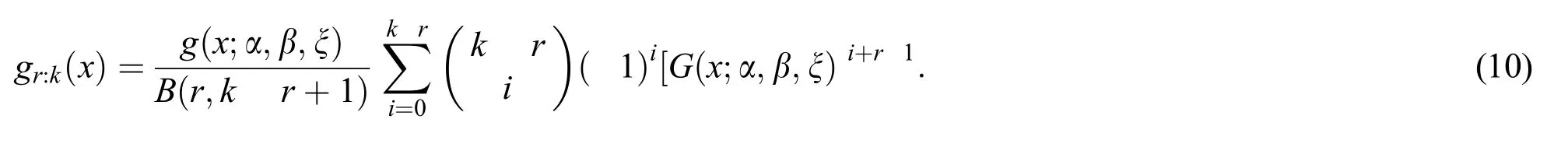
4 Maximum Likelihood Estimation
In this section,the estimation of the unknown parameters of the NL family via the method of maximum likelihood is discussed.LetX1,X2,,Xkbe a random sample from NL family with parameters(α,β,ξ).The log-likelihood function of this sample is
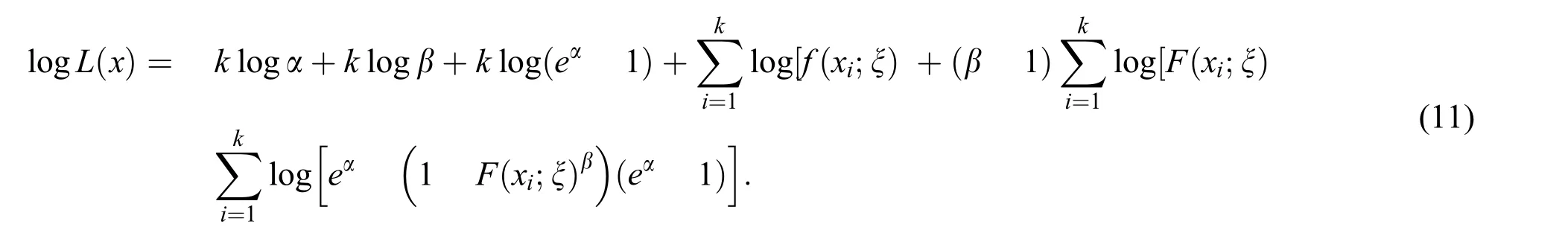
Obtaining the partial derivatives of Eq.(11),one may get
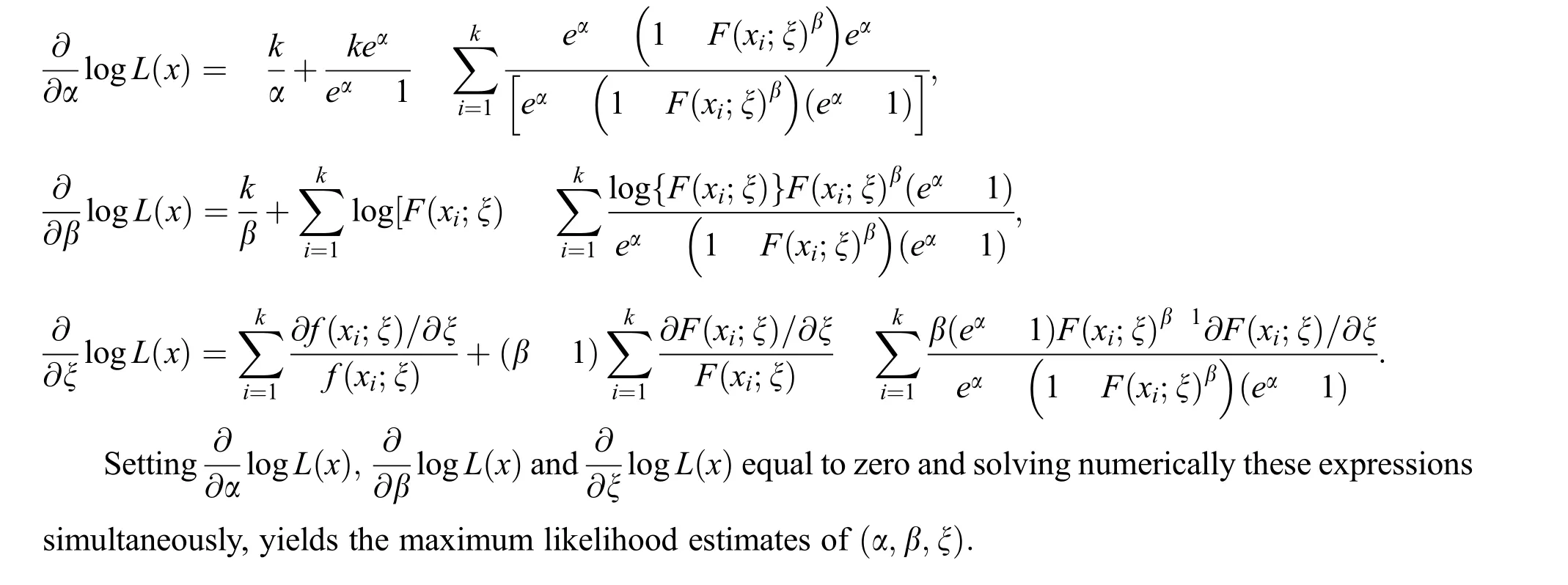
5 Monte Carlo Simulation Study

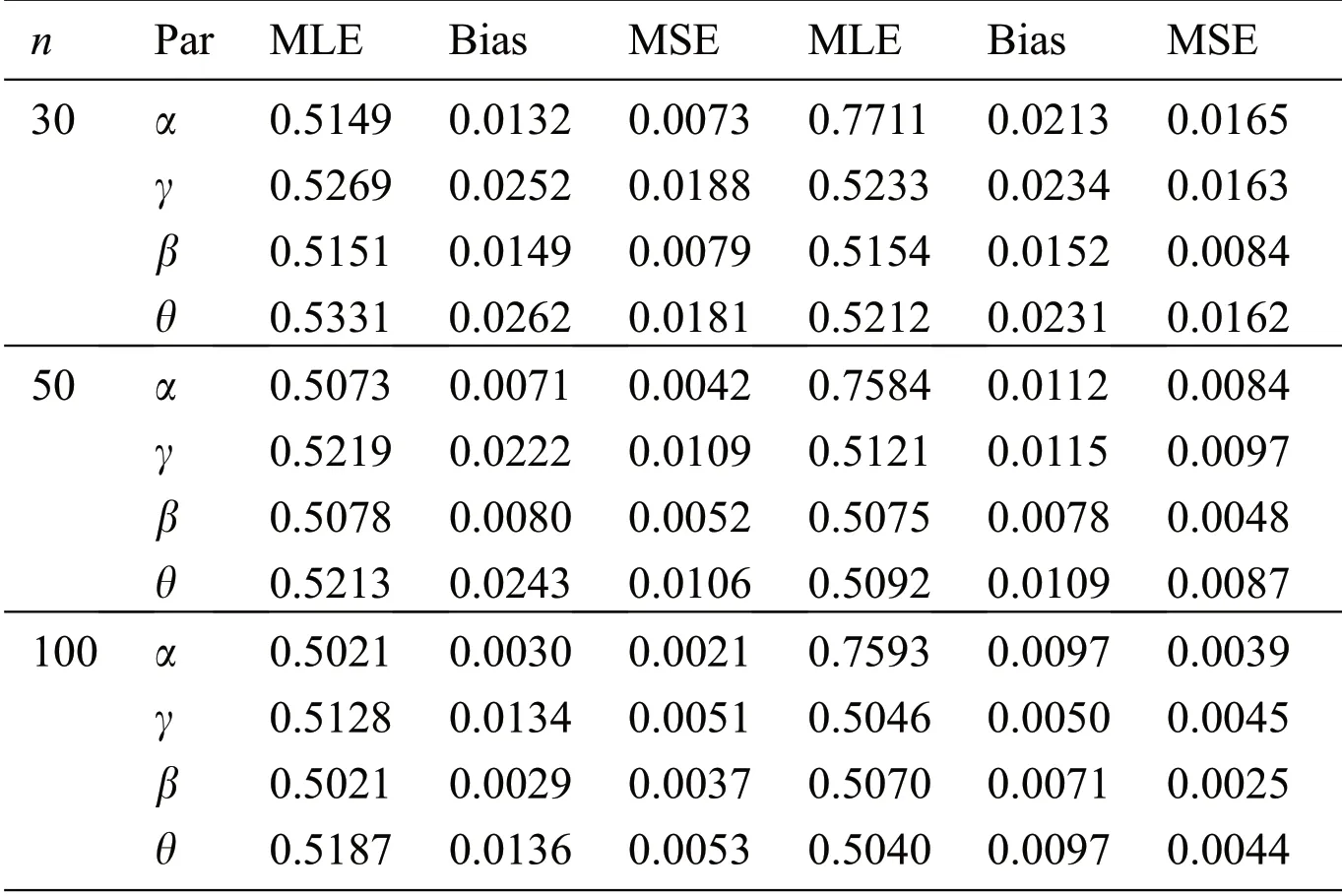
Table 1:The parameter estimation from the NLW distribution using MLE
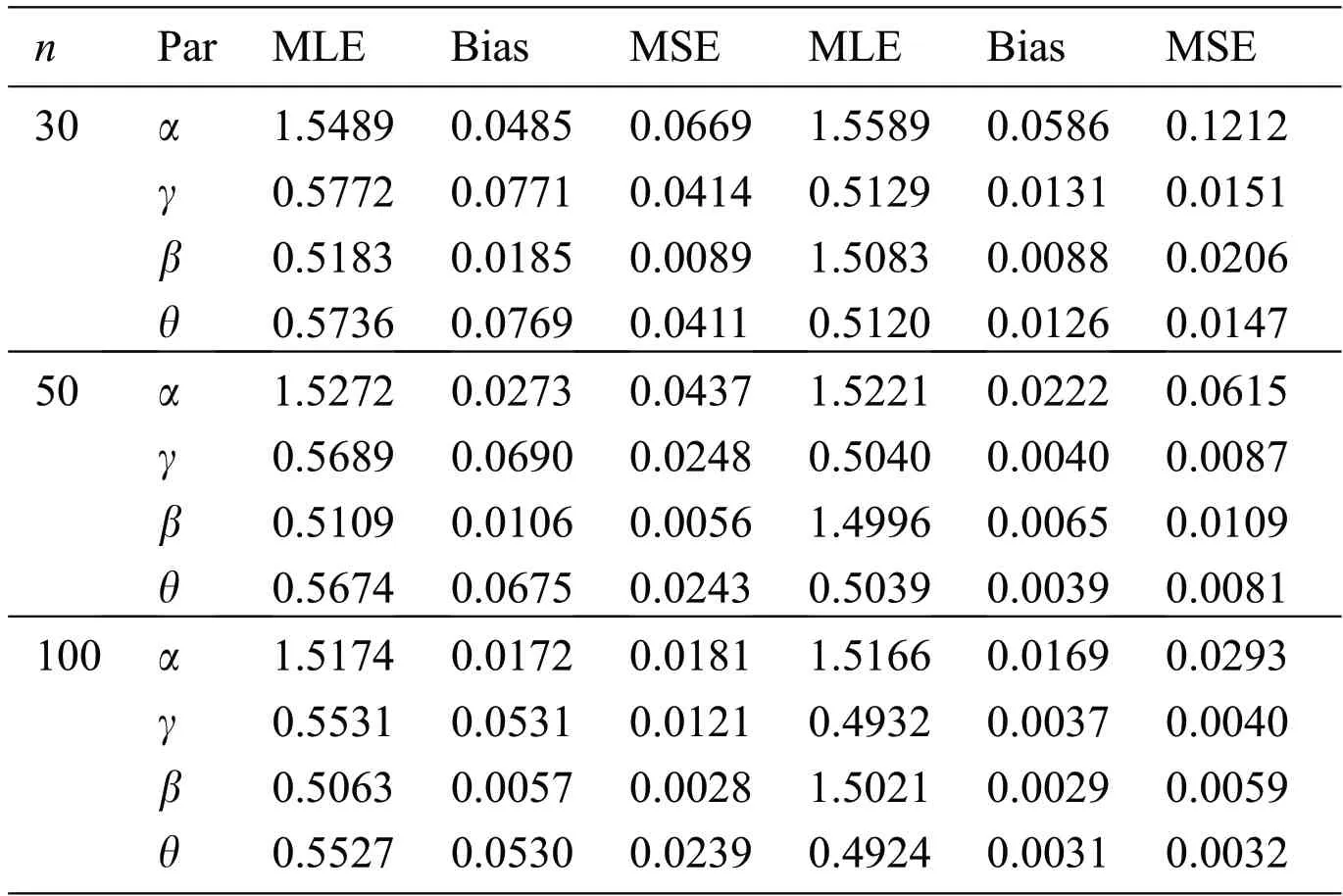
Table 2:The parameter estimation from the NLW distribution using MLE
6 Practical Applications
In this section,we provide two applications of the proposed model to the real data sets.We compare the fits of the proposed distribution to those of the three-parameter exponentiated Weibull(EW)Marshall-Olkin Weibull(MOW)and beta Weibull(BW)distributions.The goodness-of-fit measures such as Anderson-Darling(AD),Cramer–von Mises(CM),Kolmogorov-Smirnov(KS)statistic and the corresponding pvalue are considered to compare the proposed method with the fitted models.In general,a model with smaller values of these analytical measures and high p-value indicates better fit to the data.All the required computations have been carried out in the R-language using“BFGS” algorithm.
Data 1:The first data set representing the remission times(in months)of a random sample of 128 bladder cancer patients.Corresponding to data 1,the maximum likelihood estimates of the fitted models are provided in Tab.3.While,the goodness of fit measures is given in Tab.4.

Table 3:Maximum likelihood estimates of the fitted distributions using data 1
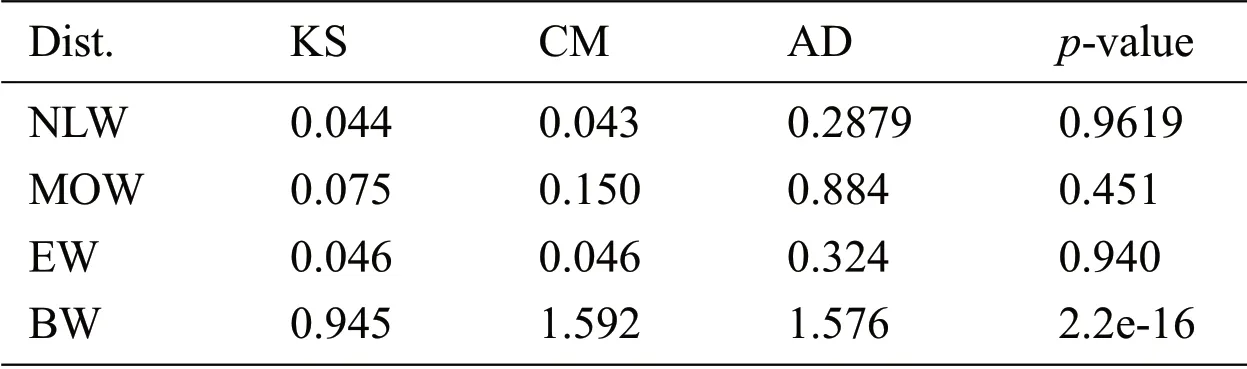
Table 4:The statistics of the fitted models using data 1
From the results given in Tab.4,it is clear that the proposed model provides the best fit to the data.Furthermore,for data 1,the estimated pdf and cdf are sketched in Fig.3,while the Kaplan-Meier survival and pp-plots are provided in Fig.4.These figures show that the proposed model fit the data very closely.

Figure 3:Plots of the estimated pdf and cdf of the NLW distribution for data 1

Figure 4:PP and Kaplan-Meir survival plots of the NLW distribution for data 1
Data 2:The second data set representing the time between failures for 30 repairable items.The maximum likelihood estimates and the considered statistics are provided in Tabs.5 and 6,respectively.Corresponding to data 2,the estimated pdf and cdf of the proposed model are plotted in Fig.5,while,the Kaplan-Meier survival and pp-plots are presented in Fig.6.These figures show how the proposed model fit the data closely.

Table 5:The maximum likelihood estimates of the fitted distributions using data 2
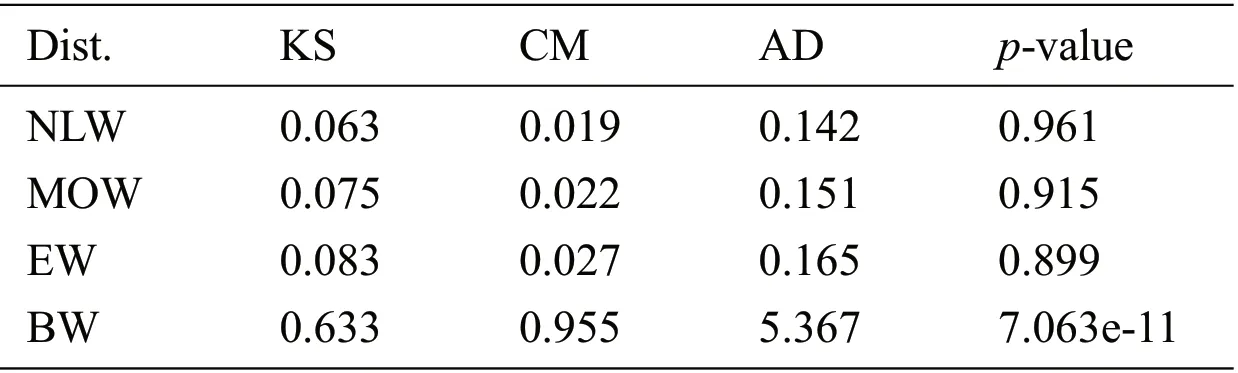
Table 6:The statistical measures of the fitted models using data 2

Figure 5:Plots of the estimated pdf and cdf of the NLW distribution corresponding to data 2
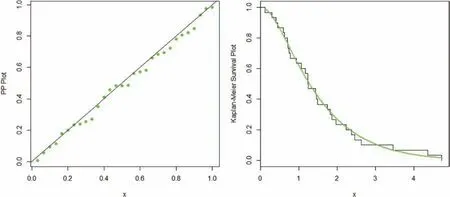
Figure 6:PP and Kaplan-Meir survival plots of the NLW distribution corresponding to data 2
7 Concluding Remarks
In this article,a new method is adopted to extend the existing distributions.This effort leads to a new family of lifetime distributions,called a new logarithmic family of distributions.General expressions for some of the mathematical properties of the new family are investigated.Maximum likelihood estimates are also obtained.There are certain advantages of using the proposed method like its cdf has a closed form solution and facilitating data modeling with monotonic and non-monotonic failure rates.A special sub-model of the new family,called a new logarithmic Weibull distribution is considered and two real applications are analyzed.In simulation study,the consistency and proficiency of the maximum likelihood estimators of the proposed model are also illustrated.The practical applications of the proposed model reveal better fits to real-life data than the other well-known competitors.It is hoped that the proposed method will attract wider applications in reliability engineering and biomedical sciences.
Funding Statement:The first and second authors acknowledge the Research on the Demand Side and Supply Side Demand Mechanism of Overcapacity Capacity of China's Machinery Manufacturing Industry in the“One Belt and One Road” Strategy,16BJY079.
Conflicts of Interest:The authors declare that they have no con icts of interest to report regarding the present study.
杂志排行
Computers Materials&Continua的其它文章
- Design of Authoring Tool for Static and Dynamic Projection Mapping
- Detecting Lumbar Implant and Diagnosing Scoliosis from Vietnamese X-Ray Imaging Using the Pre-Trained API Models and Transfer Learning
- Design of a Compact Monopole Antenna for UWB Applications
- A Smart Wellness Service Platform and Its Practical Implementation
- Fingerprint-Based Millimeter-Wave Beam Selection for Interference Mitigation in Beamspace Multi-User MIMO Communications
- Multilayer Self-Defense System to Protect Enterprise Cloud
