Computer Methodologies for the Comparison of Some Efficient Derivative Free Simultaneous Iterative Methods for Finding Roots of Non-Linear Equations
2021-12-14YumingChuNailaRafiqMudassirShamsSaimaAkramNazirAhmadMirandHumairaKalsoom
Yuming Chu,Naila Rafiq,Mudassir Shams,Saima Akram,Nazir Ahmad Mir and Humaira Kalsoom
1Department of Mathematics,Huzhou University,Huzhou,313000,China
2Department of Mathematics,National University of Modern Languages,Islamabad,Pakistan
3Department of Mathematics and Statistics,Riphah International University I-14,Islamabad,44000,Pakistan
4Center for Advanced Studies in Pure and Applied Mathematics Bahauddin Zakariya University,Multan,Pakistan
5School of Mathematical Sciences,Zhejiang University,Hanghou,310027,China
Abstract:In this article,we construct the most powerful family of simultaneous iterative method with global convergence behavior among all the existing methods in literature for finding all roots of non-linear equations.Convergence analysis proved that the order of convergence of the family of derivative free simultaneous iterative method is nine.Our main aim is to check out the most regularly used simultaneous iterative methods for finding all roots of non-linear equations by studying their dynamical planes,numerical experiments and CPU time-methodology.Dynamical planes of iterative methods are drawn by using MATLAB for the comparison of global convergence properties of simultaneous iterative methods.Convergence behavior of the higher order simultaneous iterative methods are also illustrated by residual graph obtained from some numerical test examples.Numerical test examples,dynamical behavior and computational efficiency are provided to present the performance and dominant efficiency of the newly constructed derivative free family of simultaneous iterative method over existing higher order simultaneous methods in literature.
Keywords:Non-linear equation;iterative method;simultaneous method;basins of attractions;computational efficiency
1 Introduction
One of the ancient problems in mathematics is the estimations of roots of non-linear equation

There are number of applications of non-linear equation in science and engineering.Newton’s method is a numerical iterative scheme which finds a single root at a time.The simultaneous iterative method(SIM)such as,Weirstrass[1]method is used to find all the distinct roots of Eq.(1).The iterative methods for finding single root of non-linear polynomial equation have been studied by[2–4]and many others.On the other hand,there are lot of numerical iterative methods devoted to approximate all roots of Eq.(1)simultaneously(see,e.g.,[1,5–8]and the references therein).The SIM are popular as compared to single root finding methods due to their wider range of convergence,reliability and their applications for parallel computing as well.Further details on SIM,their convergence analysis,efficiency and parallel implementations can be seen in[9,10–13]and references cited there in.The main objective of this article is to construct SIM which have more efficient and higher convergence order for approximating all distinct roots of Eq.(1).For the analysis and comparison of convergence behavior of simultaneous iterative methods,we use the techniques of dynamical plane with CAS MATLAB(R2011b).
2 Constructions of Simultaneous Method
Here,we construct a ninth order derivative free simultaneous method which is more efficient than the similar methods existing in literature.
2.1 Construction of Simultaneous Methods for Distinct Roots
Consider eighth order derivative free Kung–Traub’s[4]family of iterative method(abbreviated as KF):

Using well known Weierstrass[1]method,abbreviated as(WKD),we have:

where
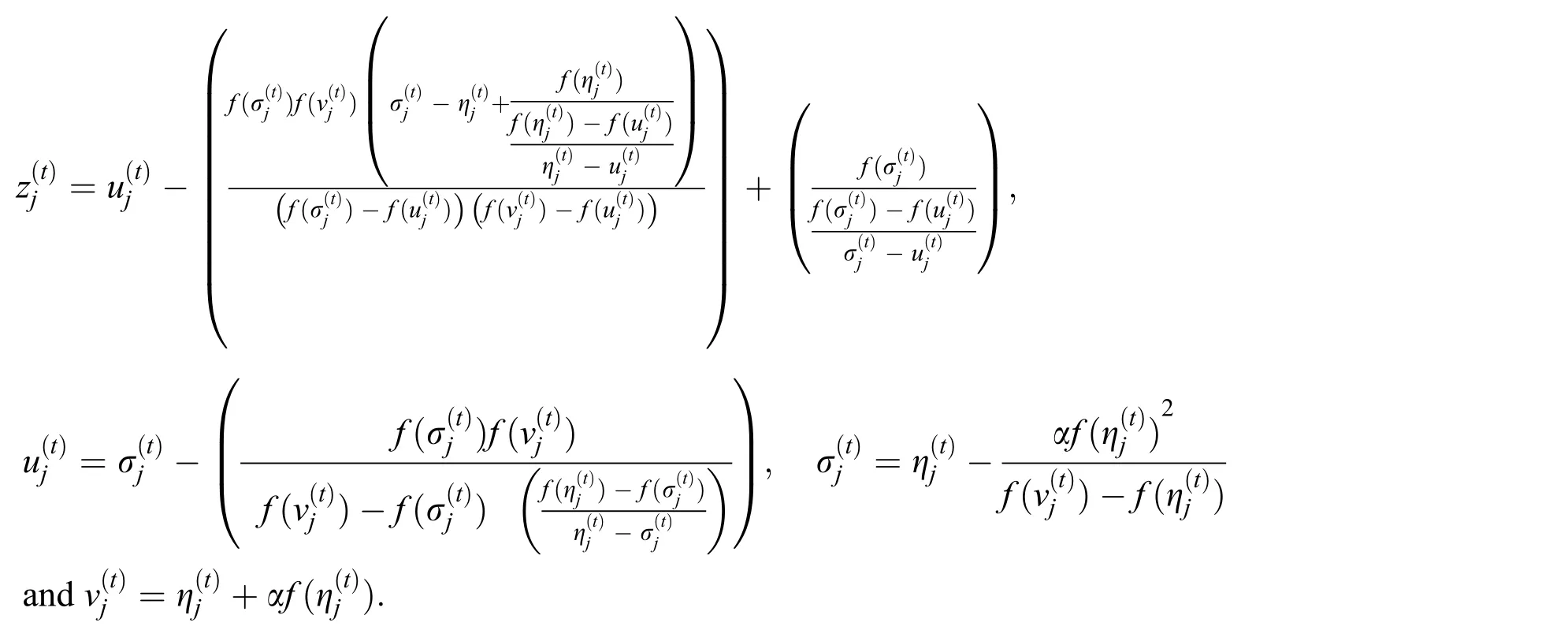
Thus,we have a new derivative free family of simultaneous method Eq.(3),abbreviated as SIM1,for approximating all the distinct roots of Eq.(1).
2.2 Convergence Analysis

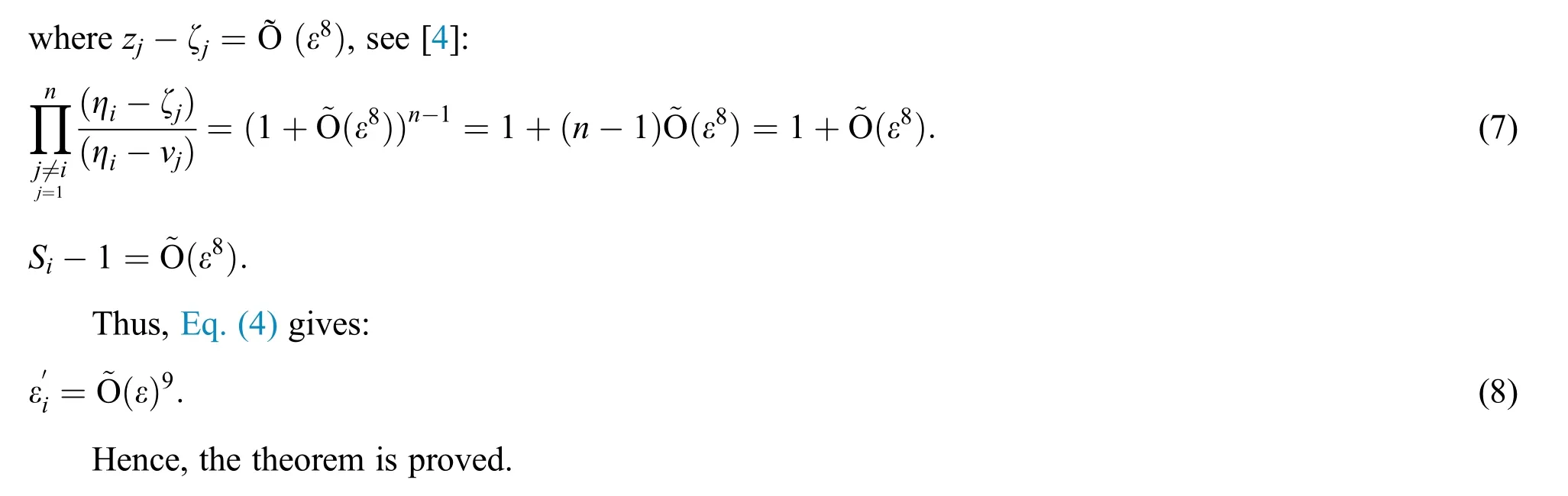
3 Dynamical Studies of KF,SIM1 and SPJ1

4 Computational Aspects

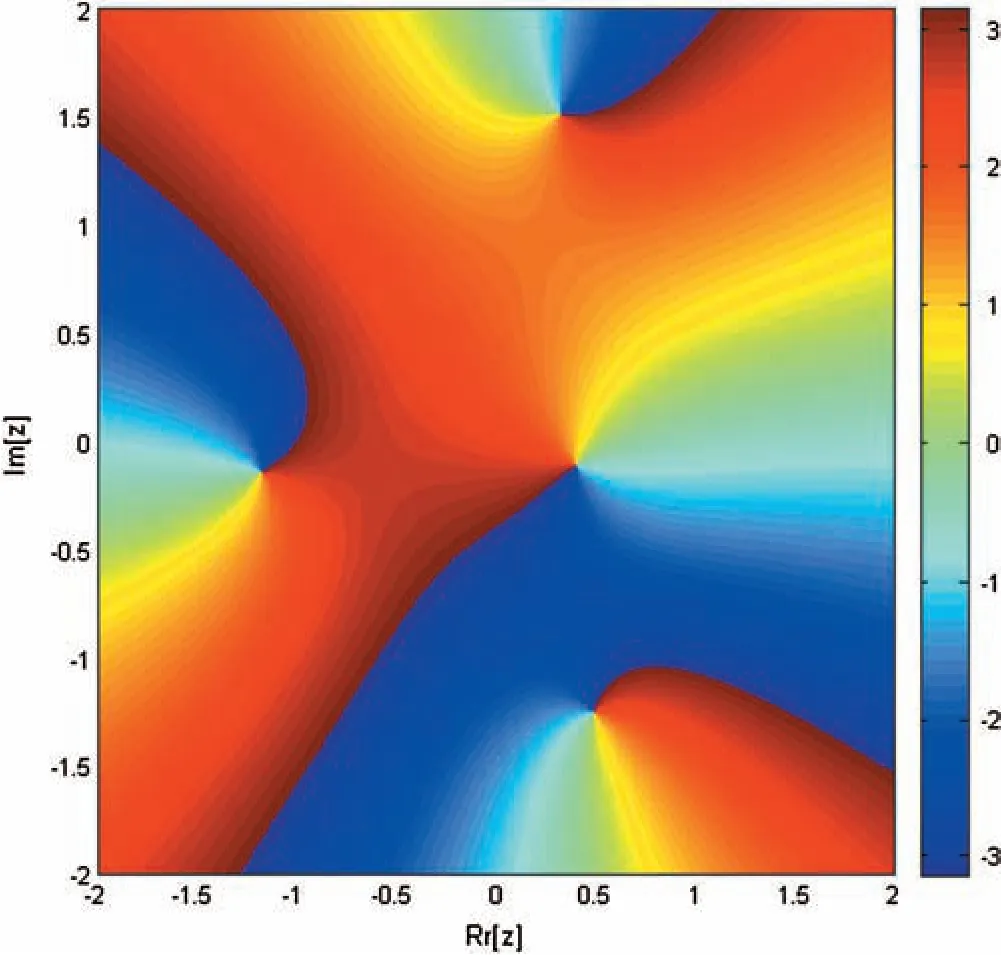
Figure 1:Basin of attraction of iterative method SIM1 for non-linear equation f1(η)=η4+η2+η-1
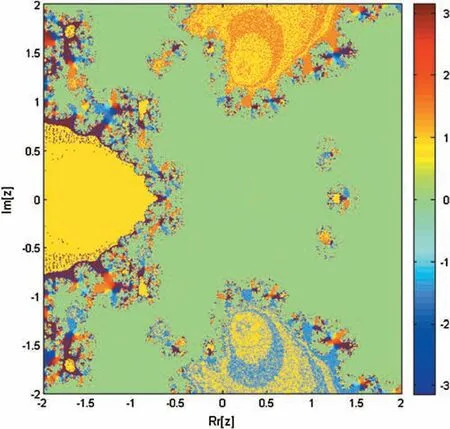
Figure 2:Basin of attraction of iterative method KF for non-linear equation f1(η)=η4+η2+η-1
Thus,Eq.(9)becomes:

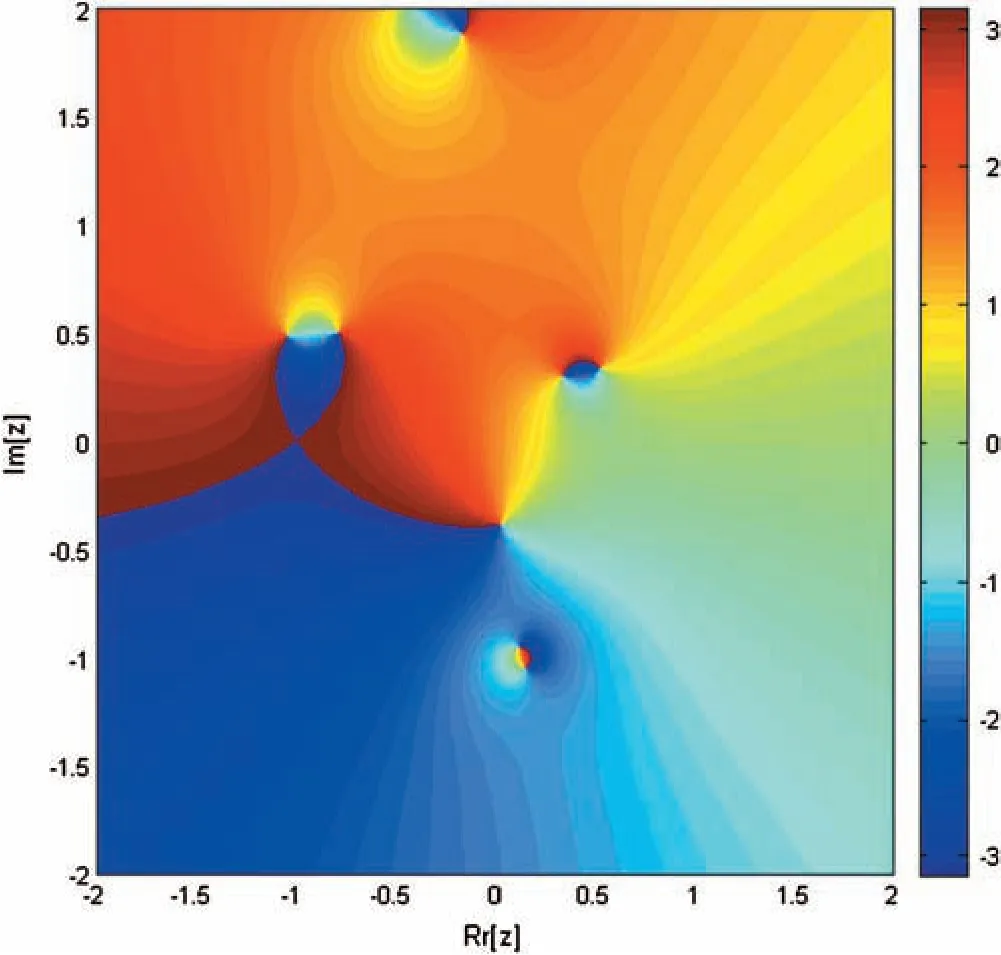
Figure 3:Basin of attraction of iterative method SPJ1 for non-linear equation f1(η)=η4+η2+η-1
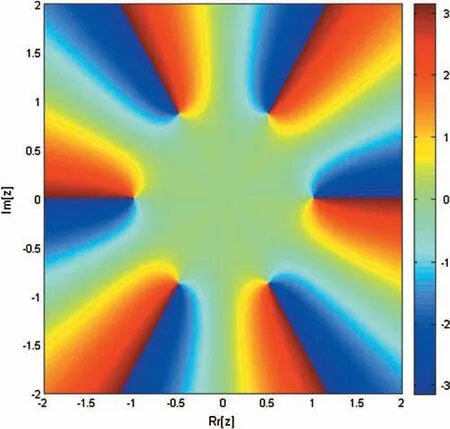
Figure 4:Basin of attraction of iterative method SIM1 for non-linear equation f2(η)=η6+η-1
Using Eq.(11)and data in Tab.1,we find the percentage ratio Ω(SIM1,SPJ1)[14]as:

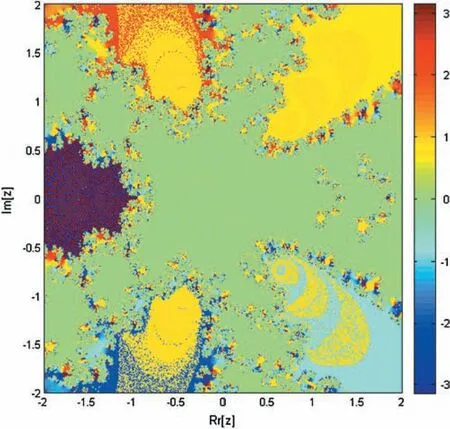
Figure 5:Basin of attraction of iterative method KF for non-linear equation f2(η)=η6+η-1

Figure 6:Basin of attraction of iterative method SPJ1 for non-linear equation f2(η)=η6+η-1

Figs.11–12,graphically illustrates these percentage ratios.Figs.11–12,clearly show that the newly constructed simultaneous method SIM1 is more efficient as compared to Petkovic method(SPJ1).
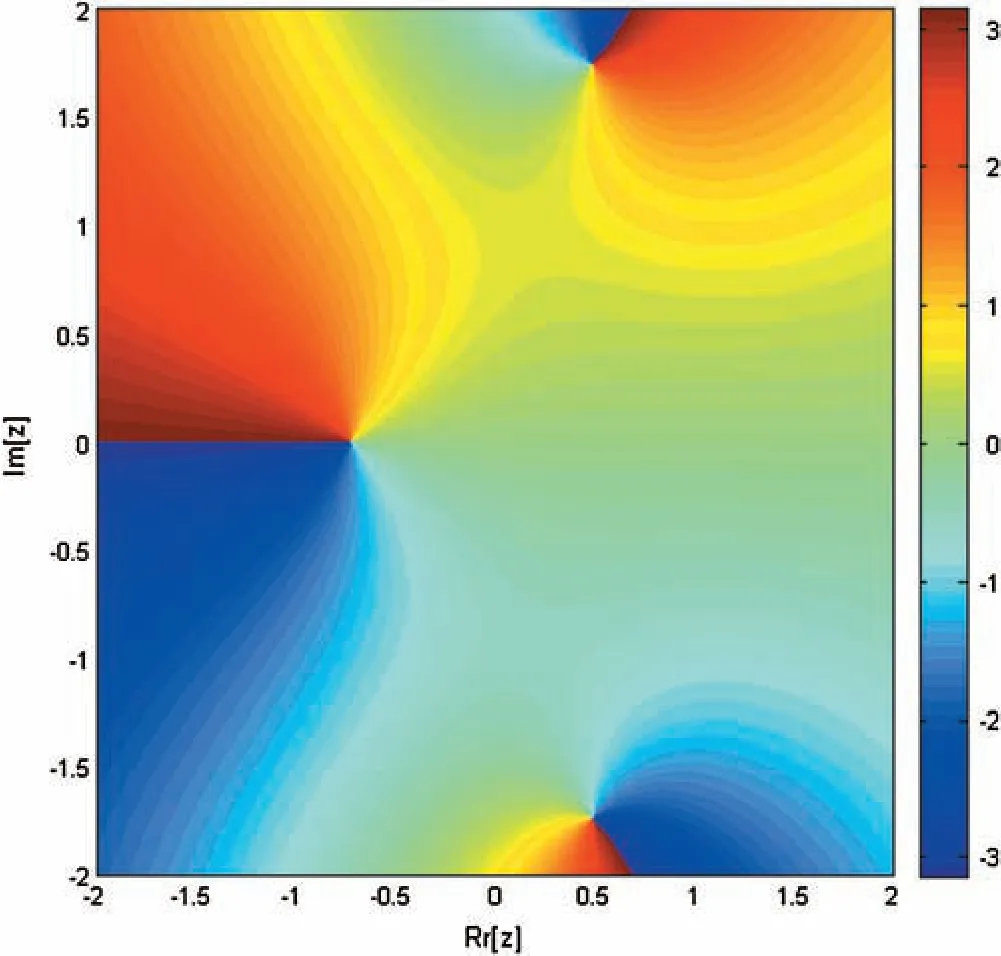
Figure 7:Basin of attraction of iterative method SIM1 for non-linear equation
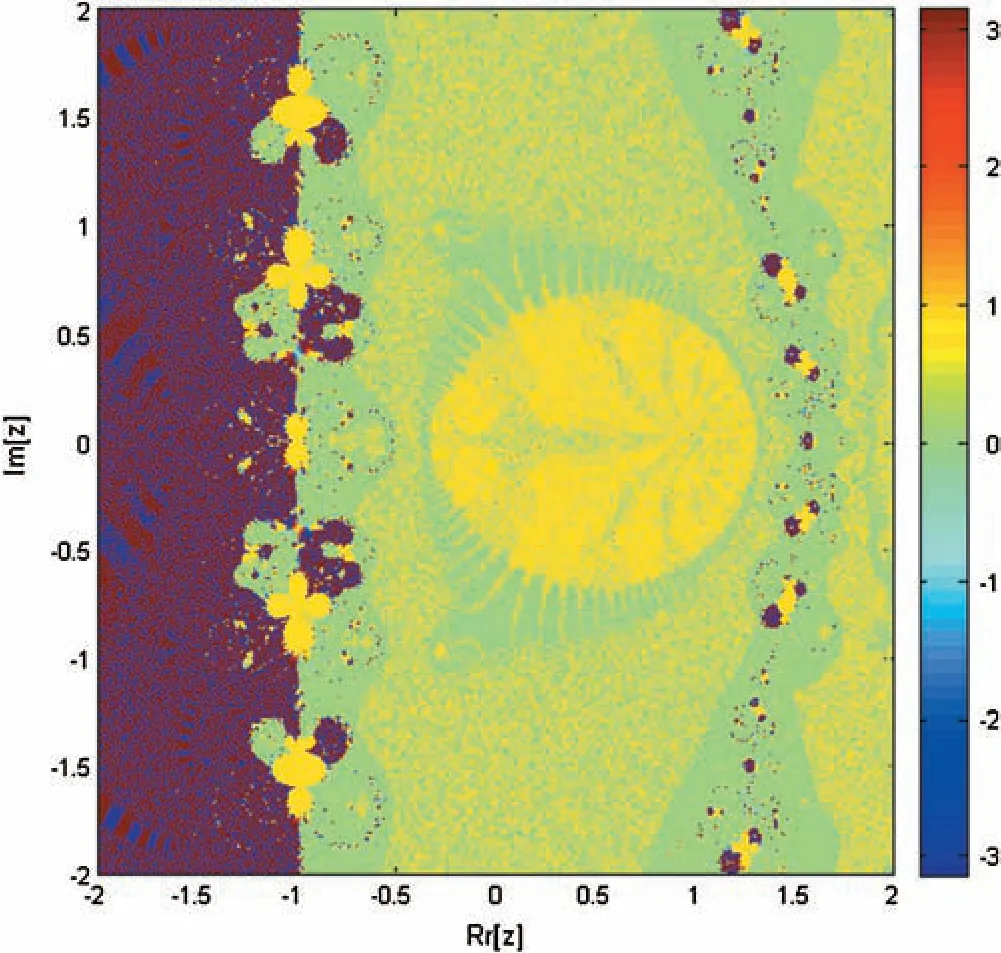
Figure 8:Basin of attraction of iterative method KF for non-linear equation
5 Numerical Results
Here,some numerical test examples are considered in order to show the performance of simultaneous ninth order derivative free method SIM1.We compare our method with[14]method(SPJ1)of convergence order ten for distinct roots.All the numerical calculations are done by using Maple 18 with 64 digits floating point arithmetic.We take ∈=10-30as tolerance and use as a stopping criteria.
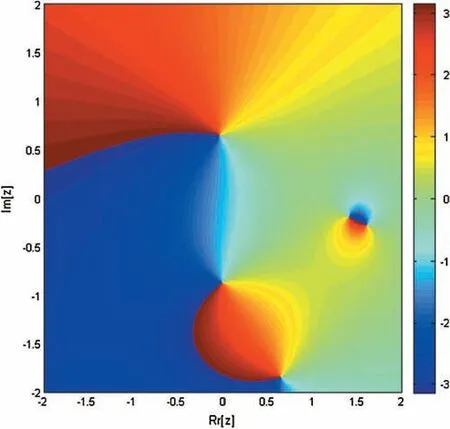
Figure 9:Basin of attraction of iterative method SPJ1 for non-linear equation
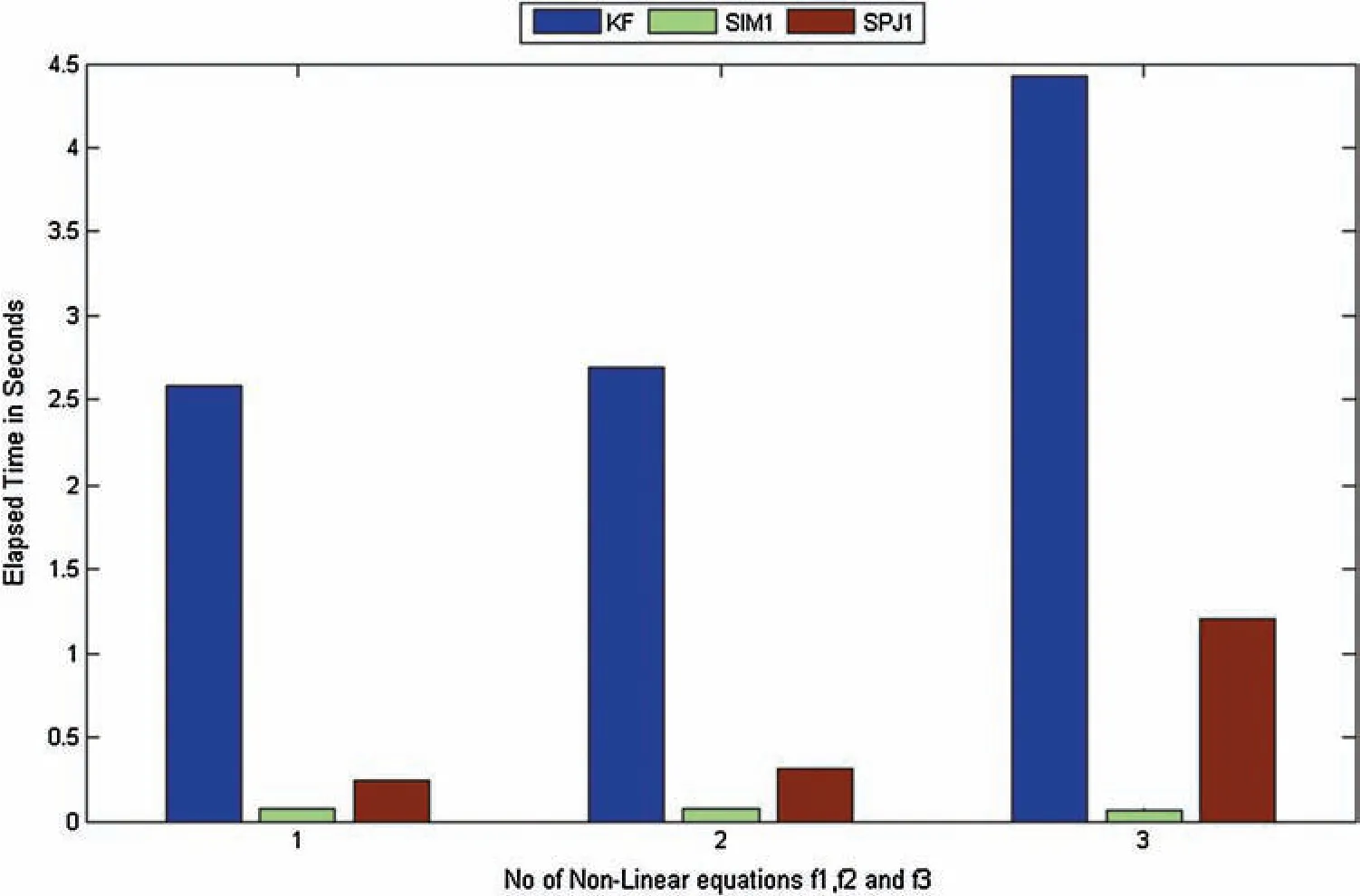
Figure 10:Elapsed time of iterative methods SIM1,KF,SPJ1 in seconds for non-linear function f1(η),f2(η)and f3(η)respectively
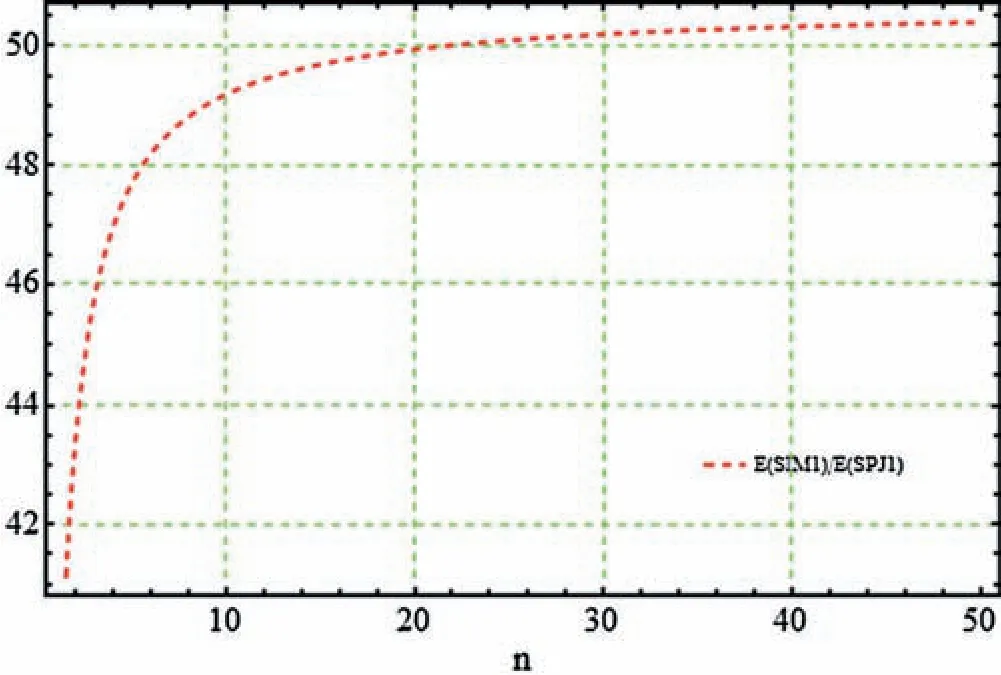
Figure 11:Computation efficiency of SIM1 w.r.t.SPJ1
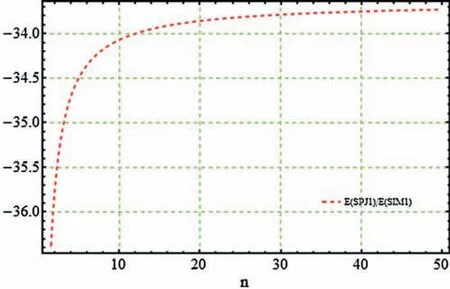
Figure 12:Computation efficiency of SPJ1 w.r.t.SIM1

Tests examples from[16–18]are provided in Tabs.2–3.In all Tables,CO denotes the order of convergence,α,parameter valued in SIM1,n,the number of iterations andCPU,execution time in seconds.Figs.13–16,show that residue fall of the methodsSIM1 andSPJ1 for the numerical test examples 1-2,shows that methodSIM1 is more efficient as compared toSPJ1.We observe that numerical results of the methodSIM1 are comparable withSPJ1 method on same number of iteration.

Table 1:The number of basic arithmetic operations

Table 2:Simultaneous determination of all roots f4(η)
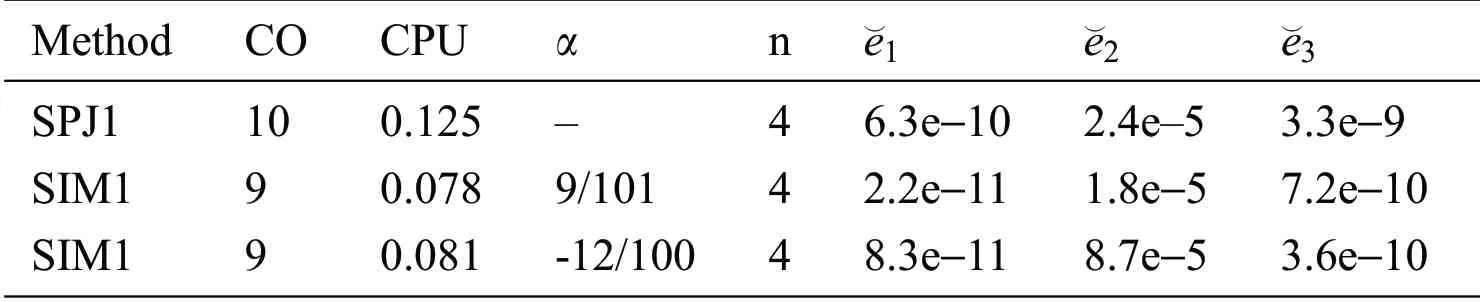
Table 3:Simultaneous determination of all roots f5(η)
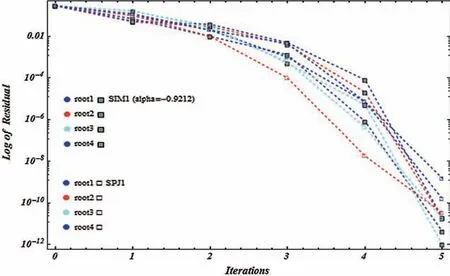
Figure 13:Shows residual graph of SIM1(α=-0.9212)and SPJ1 for non-linear function f4(η)
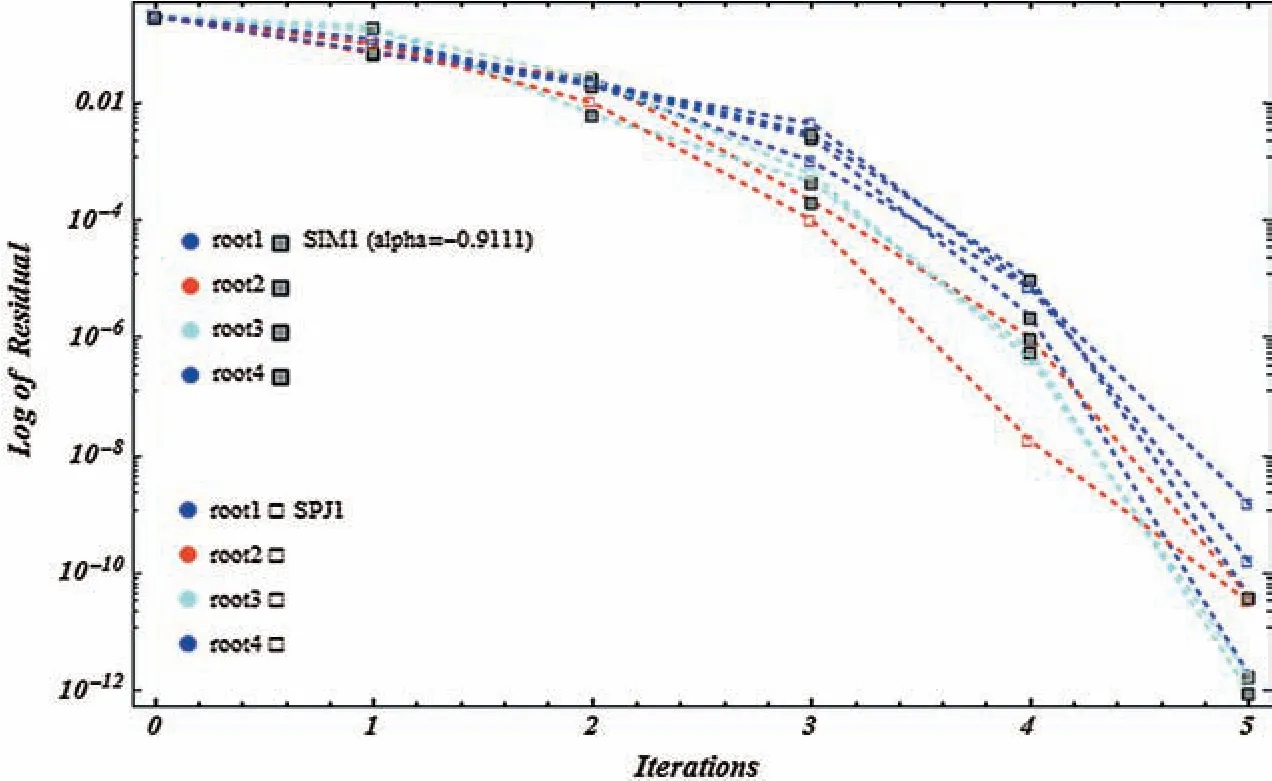
Figure 14:Shows residual graph of SIM1(α=-0.9111)and SPJ1 for non-linear function f4(η)
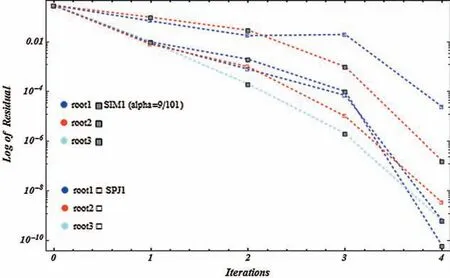
Figure 15:Shows residual graph of SIM1 and SPJ1 for non-linear function f5(η)
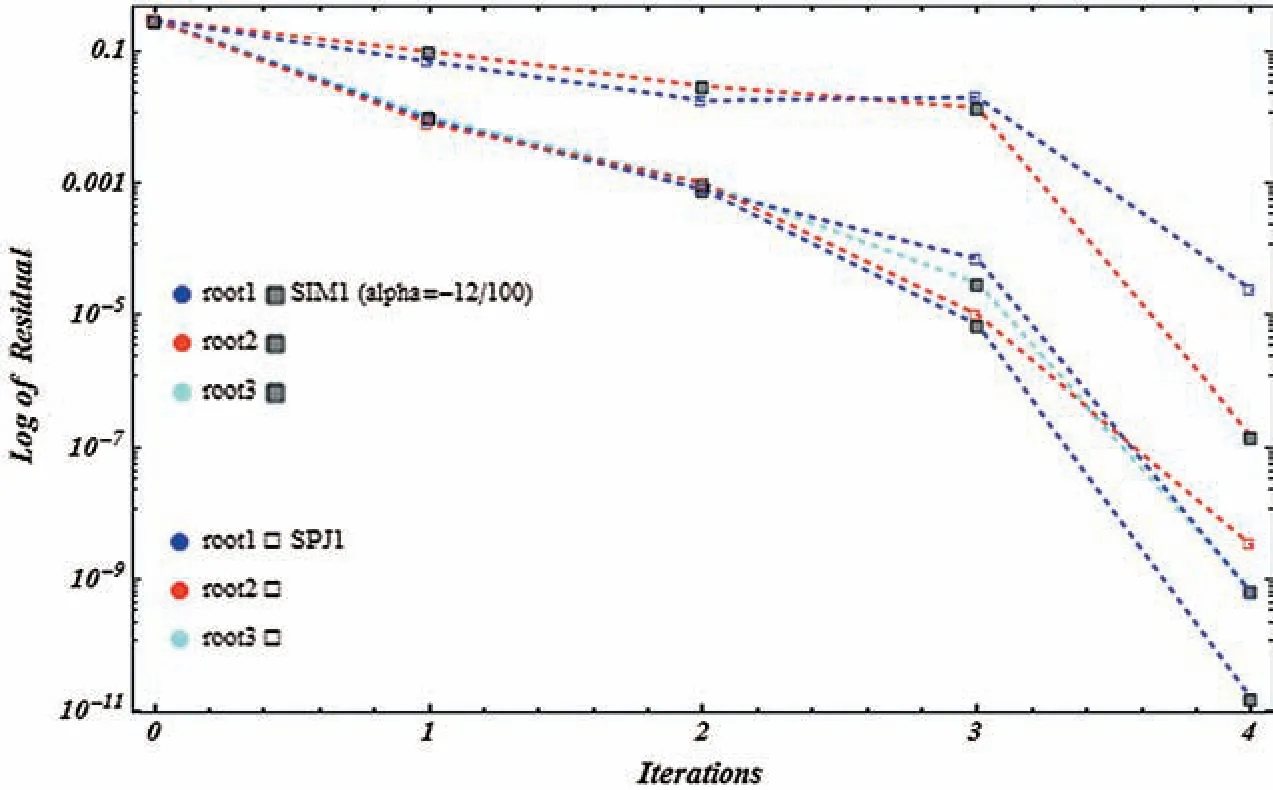
Figure 16:Shows residual graph of SIM1 and SPJ1 for non-linear function f5(η)
We also calculate the CPU execution time,as all the calculations are done using Maple 18 on(Processor Intel(R)Core(TM)i3-3110m CPU@2.4 GHz with 64-bit Operating System).We observe from Tables that CPU time of the methods SIM1 is comparable or better than method SPJ1,showing the efficiency of our family of derivative free methods SIM1 as compared to them.

Table 4:Simultaneous determination of all roots f6(η)
Algorithm for simultaneous iterative method


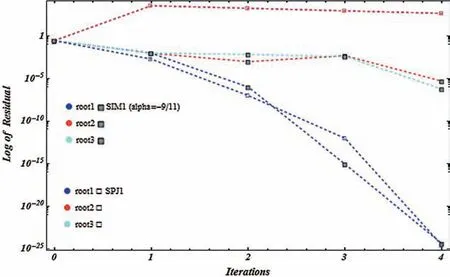
Figure 17:Shows residual graph of SIM1 and SPJ1 for non-linear function f6(η)
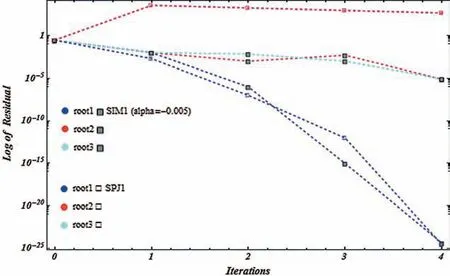
Figure 18:Shows residual graph of SIM1(α=-0.005)and SPJ1 for non-linear function f6(η)
6 Conclusions
We have developed here derivate free family of simultaneous methods of order nine for determining all the roots of non-linear equations.It must be pointed out that so far there exists derivative free method of order four only in the literature.We have made here comparison with method SPJ1 of order 10 involving derivative.The dynamical behavior/basins of attractions of our family of simultaneous methods SIM1 is also discussed here to show the global convergence.An example of single root finding derivative free method of order 8 of King–Traub is discussed to show that the single root finding methods may have divergence region.The computational efficiency of our method SIM1 is very large as compare to the method SPJ1 as given in Tabs.2–4,which is also obvious from Figs.11–12.We have made the numerical comparison with SPJ1 method.From Tabs.2–4 and Figs.1,4,7,13–18,we observe that our numerical results are comparable or better in term of absolute error,number of iterations and CPU time and for log of residual graphs and lapsed time of dynamical planes.
Acknowledgement:The work is supported by the Natural Science Foundation of China(Grant Nos.61673169,11301127,11701176,11626101,and 11601485)and The Natural Science Foundation of Huzhou City(Grant No.2018YZ07).
Funding Statement:The article processing charges(APC)will be paid by Natural Science Foundation and Natural Science Foundion of Huzhou City,China.
Confilcts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
杂志排行
Computers Materials&Continua的其它文章
- Design of Authoring Tool for Static and Dynamic Projection Mapping
- Detecting Lumbar Implant and Diagnosing Scoliosis from Vietnamese X-Ray Imaging Using the Pre-Trained API Models and Transfer Learning
- Design of a Compact Monopole Antenna for UWB Applications
- A Smart Wellness Service Platform and Its Practical Implementation
- Fingerprint-Based Millimeter-Wave Beam Selection for Interference Mitigation in Beamspace Multi-User MIMO Communications
- Multilayer Self-Defense System to Protect Enterprise Cloud
