Dual Branches of MHD Three-Dimensional Rotating Flow of Hybrid Nanofluid on Nonlinear Shrinking Sheet

Liaquat Ali Lund,Zurni Omar,Ilyas Khan and El-Sayed M.Sherif

1School of Quantitative Sciences,Universiti Utara Malaysia,Sintok,Kedah,06010,Malaysia

2KCAET Khairpur Mir’s,Sindh Agriculture University,Tandojam,Sindh,70060,Pakistan

3Faculty of Mathematics and Statistics,Ton Duc Thang University,Ho Chi Minh City,Vietnam

4Center of Excellence for Research in Engineering Materials,King Saud University,Al-Riyadh,11421,Saudi Arabia

5Electrochemistry and Corrosion Laboratory,Department of Physical Chemistry,National Research Centre,Dokki,Cairo,12622,Egypt

Abstract:In this study,magnetohydrodynamic(MHD)three-dimensional(3D)flow of alumina(Al2O3)and copper(Cu)nanoparticles of an electrically conducting incompressible fluid in a rotating frame has been investigated.The shrinking surface generates the flow that also has been examined.The single-phase(i.e.,Tiwari and Das)model is implemented for the hybrid nanofluid transport phenomena.Results for alumina and copper nanomaterials in the water base fluid are achieved.Boundary layer approximations are used to reduce governing partial differential(PDEs)system into the system of the ordinary differential equations(ODEs).The three-stage Lobatto IIIa method in bvp4c solver is applied for solutions of the governing model.Graphical results have been shown to examine how velocity and temperature fields are influenced by various applied parameters.It has been found that there are two branches for certain values of the suction/injection parameter b.The rise in copper volumetric concentration improved the velocity of hybrid nanofluid in the upper branch.The heat transfer rate improved for the case of hybrid nanofluid as compared to the viscous fluid and simple nanofluid.

Keywords:Nonlinear surface;viscous dissipation;MHD;Hybrid nanofluid;two branches

1 Introduction

A modern procreation liquid of strong thermal efficiency is useful in fulfilling industrial and technical needs.In the past,Choi et al.[1]developed nano-liquids and revealed that nanoparticles dispersion can improve the normal fluids’ thermal conductivity.At present,dispersions of nanoparticles have been highly discussed topics for sophisticated heat engineering owing to their exceptional efficiency and subphenomenon of this kind of employed liquid.Graphene is among nanomaterials that have gained more consideration owing to its high heat capacity and strong stability when distributed in traditional fluids(ethylene glycol or water)with low thermal efficiency.Sheikholeslami et al.[2]numerically examined the 3D flow of nanofluid with the magnetic effect.Hayat et al.[3]analytically studied the radiative MHD flow of viscoelastic nanofluid and found that radiation helps to improve the thermal conductivity and temperature of the fluid.Articles of the implementations,formulation,and thermomechanical characteristics of hybrid nanofluids were already undertaken by the following researchers:Subhani et al.[4],Qi et al.[5]and Islam et al.[6].

Due to the importance and demand of the heat transfer rate,researchers have introduced a hybrid nanofluid.Hybrid nanofluid appears to be a mixture of the regular fluid,which are gas,ethylene glycol,water,a blend of water and ethylene glycol,and two distinct classes of nanomaterials,which are carbon materials,metals,and metal oxides.A model for analyzing the heat capacity of hybrid nanofluids specifically in carbon nanotubes has been established by Esfe et al.[7].Carbon nanotubes were chosen for the processing of hybrid nanofluid because of their high effect on thermal performance.Copper and aluminum pairs are both commonly utilized in experimental and theoretical research of synthetic nanofluids.Al2O3provides poor thermal conductivity;nonetheless,strong chemical action in alumina may preserve the durability of the hybrid nanofluid[8].In addition,the computational analyses of hybrid nanofluid have been applied to the problem of boundary layer movement.Initially,the fluid flow on a stretching sheet with alumina-copper/water hybrid nanofluid has been considered in this paper[9].They noticed that rise in heat transfer occurred at higher rates of nanomaterials volume fraction.Also,in a series of publications,Lund et al.[10–13]extended the problems of hybrid nanofluid flow to multiple physical effects,considering the multiple solutions.In addition,some scholars have also addressed the flow of hybrid nanofluid’s problem along with specific physical conditions[14–17].Besides,the usage of hybrid nanofluid will expand the heat rate attributed to the harmonious impacts mentioned by Sarkar et al.[18].Owing to its potential to increase heat transfer rate,most utilizations involving heat transfer,like coolant in electronic and machining and transmitter conserving,regard hybrid nanofluid as heat transfer fluid.

The rotational 3D flow on the shrinking sheet coupled with the heat transfer rate has a huge application in biomedical,chemical,and manufacturing processes.Various uses of hybrid nanofluid are not possible without consideration of the effect of MHD.Recently,encouraging finding is the usage of MHD in cancer care drug targeting[19].Hayat et al.[20]considered the 3D flow with the effect of MHD in rotational fluid flow on the stretching surface.They found that temperature reduced when Pr increased.Shah et al.[21]used the two-phase model of the nanofluid with the effect of Brownian motion in the rotating system.Hayat et al.[22]examined the nanofluid by using of the single-phase model with consideration of Darcy-Forchheimer porous medium effect.

The goal of this research is therefore to investigate the rotating angular effects of the hybrid nanofluid 3D flow across the magnetic field with viscous dissipation using the Tiwari et al.[23]models.To the best of the authors’knowledge,no such study has yet been considered.It can be said that this work is the extension of the work of Hayat et al.[20]and Hayat et al.[22]for the hybrid nanofluid on the nonlinear shrinking sheet where water is used as the base fluid,and alumina(first nanoparticles)and copper(second nanoparticles)are taken into account for hybrid nanomaterials.The findings are gotten for many applied parameters and described graphically.In addition,this whole theoretical framework would help several other engineers and scholars to explore the challenge facing the modern industry in terms of the rate of heat transfer and the need for coolant.

2 Mathematical Formulation

We have considered the steady,MHD,three-dimensional flow of hybrid nanofluid along with heat transfer past a flat plate.The sheet atz=0 is shrinking nonlinearly inx-axis direction i.e.,uw(x)=-cxn.Mass flux of velocity istemperature within boundary layer isTw=T∞+T0x2nand outside the boundary layer isT∞.Water and sheet both are rotating having angular velocity ˜Ω=Ω0x(1-n)about thez-axis taken normal to the sheet.Inz-direction,a uniform field of magnetic is placed,i.e.,B=B0x(1-n)/2.It results in magnetic effects in thex-axis andz-axis directions.The magnetic Reynolds number has been supposed very low and the field of induced magnetic has been ignored.Considering the momentum along with temperature boundary layers equations of hybrid nanofluid flow are described as

The related boundary conditions(BCs)of Eqs.(1)–(5)are

whereu,v,andware the respective components of velocity inx,yandz-axes directions,σhnfis the electrical conductivity of the hybrid nanofluid,andPis the modified pressure including the centrifugal force term.Further,and,ρhnfare the corresponding heat capacity,dynamic viscosity,thermal conductivity,and density of hybrid nanofluid.Moreover,subscripthnfshows the thermophilic properties of hybrid nanofluid.Further,the viscous dissipation function can be expressed as Φ.

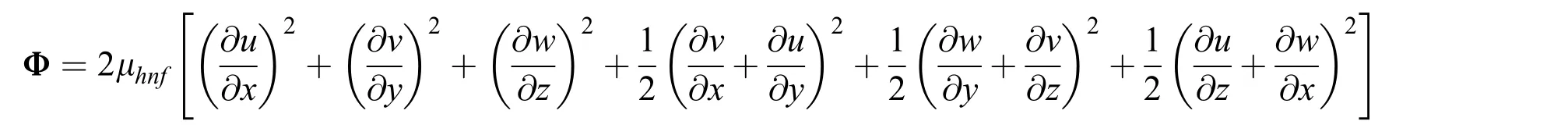
The thermophysical properties are given in Tabs.1–2.

We will employ similarity variables(7)in Eqs.(1)–(5)in order to obtain similarity solutions.

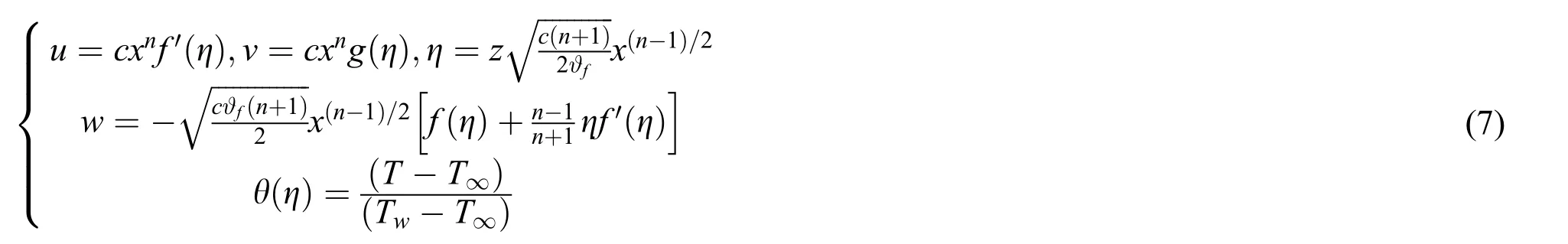
substitute Eq.(7)in(2)–(6),it is obtained

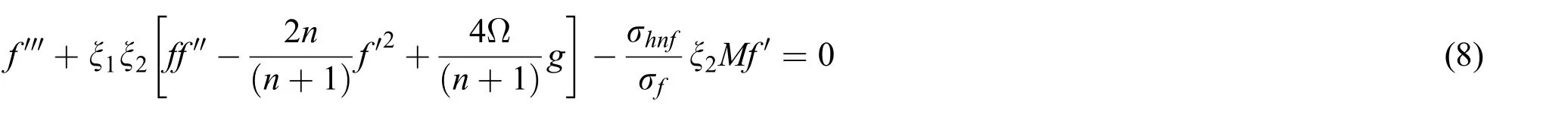
Table 1:Thermophysical features of hybrid nanofluid

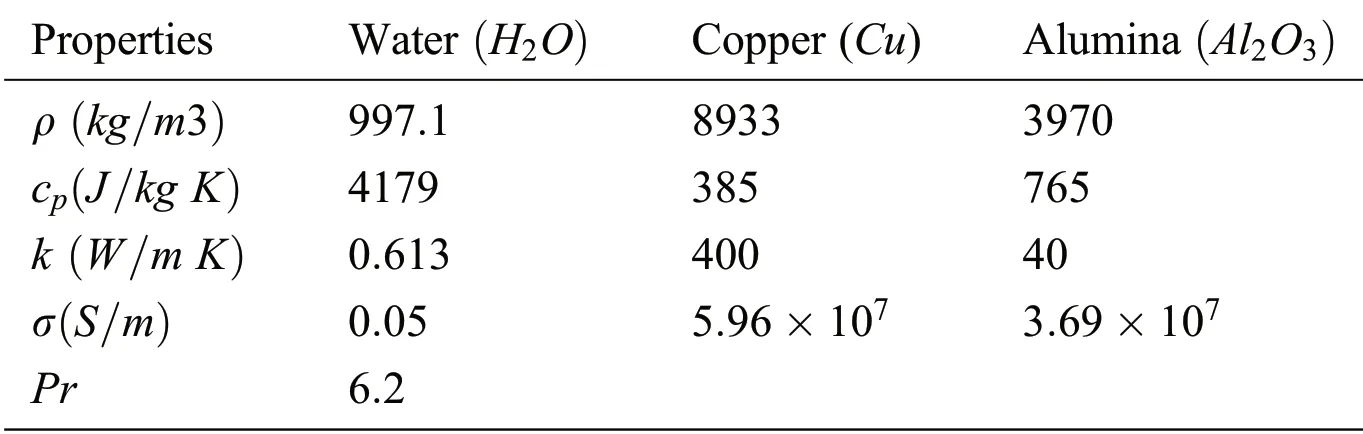
Table 2:The properties of thermo physical

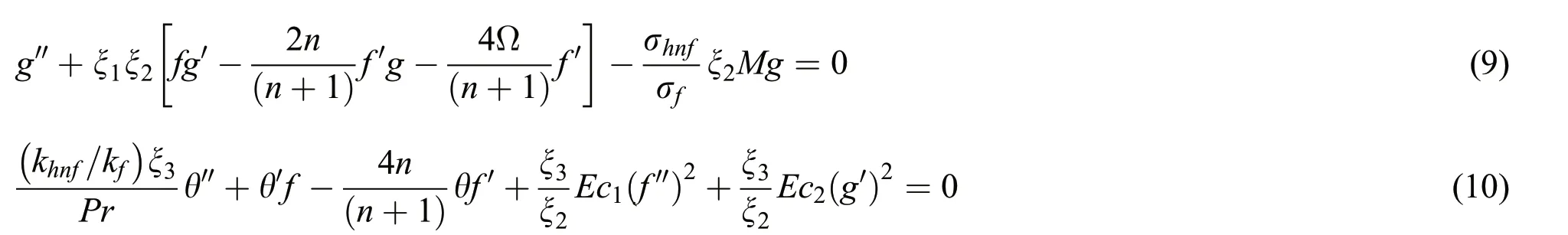
Along with BCs

By substituting Eq.(7)in Eq.(14),it is obtained

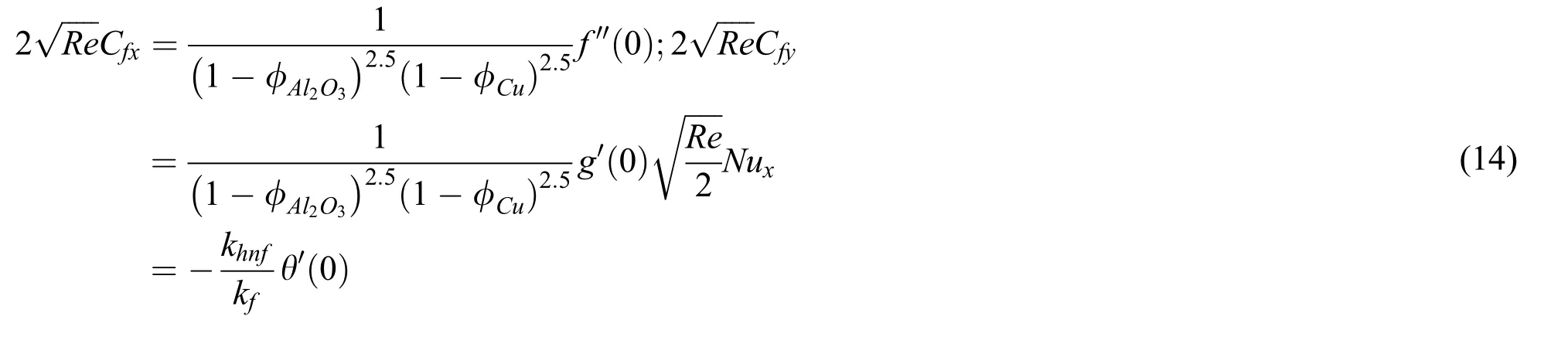
whereRexis the local Reynold number.

3 Results and Discussion

By using MATLAB program with its outstandingbvp4cfunction,similarity multiple branches have been gotten by solving Eqs.(8)–(10)along with BCs Eq.(11).This solver is made with help of a collocation technique that contains 4thorder accuracy.Thebvp4csolver will function reliably to forecast branches by employing the pair of random initial assumptions,yet,average processor time for computing results can vary based on the use of the original assumptions.The thickness of boundary layer η∞=8,Pr=6.2(for water water at room temperature 25°C),the solid volume fraction of alumina ϕAl2O3=0.1 have been kept in the whole study,whereas appropriate initial assumptions for code ofbvp4cand values of other physical quantities have been selected till the velocity and temperature profiles meet the BCs Eq.(11)asymptotically at η →∞.We have set the error of the relative tolerance 10-10which is acceptable scientifically for the excellent accuracy.The system of governing Eqs.(8)–(10)are reduced as follows:

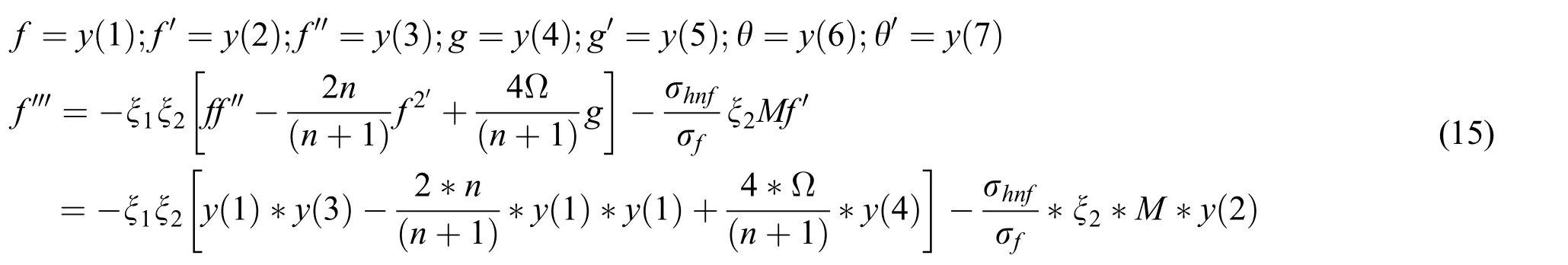
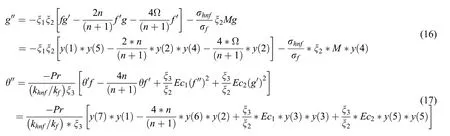
and BCs

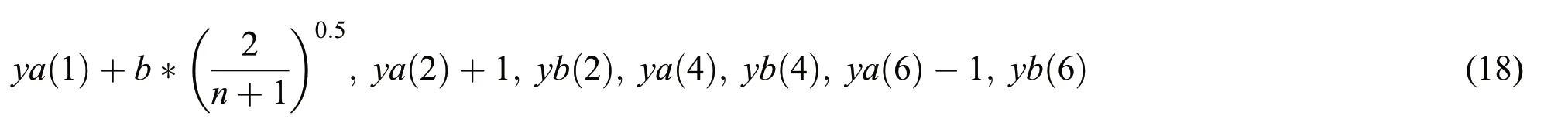
whereyashows the initial condition andybshows the far-field condition.The full description of thebvp4csolver can be read in Lund et al.[24,25].

Two branches of Eqs.(8)–(10)are noticed whenb≤bcand no similarity branch could be found forb＞bc,as revealed in Figs.1–7.Figs.1–3 show the effect of ϕCuon skin friction coefficient(f′′(0),g′(0))and heat transfer rate(-θ′(0))against the various values ofb.Two branches occur for the suction/injection parameterb≤bcwherebc1=-2.4067,bc2=-2.3004 andbc3=-2.2272 are the corresponding critical values of ϕCu=0.01,0.05 and 0.1.It should be noted that both branches exist at the pointbc.The first branch,magnitudes off′′(0)andg′(0)increase when ϕCuis increased but reduce as the effect of suction goes toward to injection effect.On another side,the contrary pattern off′′(0)andg′(0)has been found in the lower branch.In Fig.3,the magnitude of -θ′(0)is high when the volume fraction of the copper nanoparticles is 1% as compared to 5% and 10% in the upper branch.While the heat transfer rate increases whenbenhances in the lower branch.

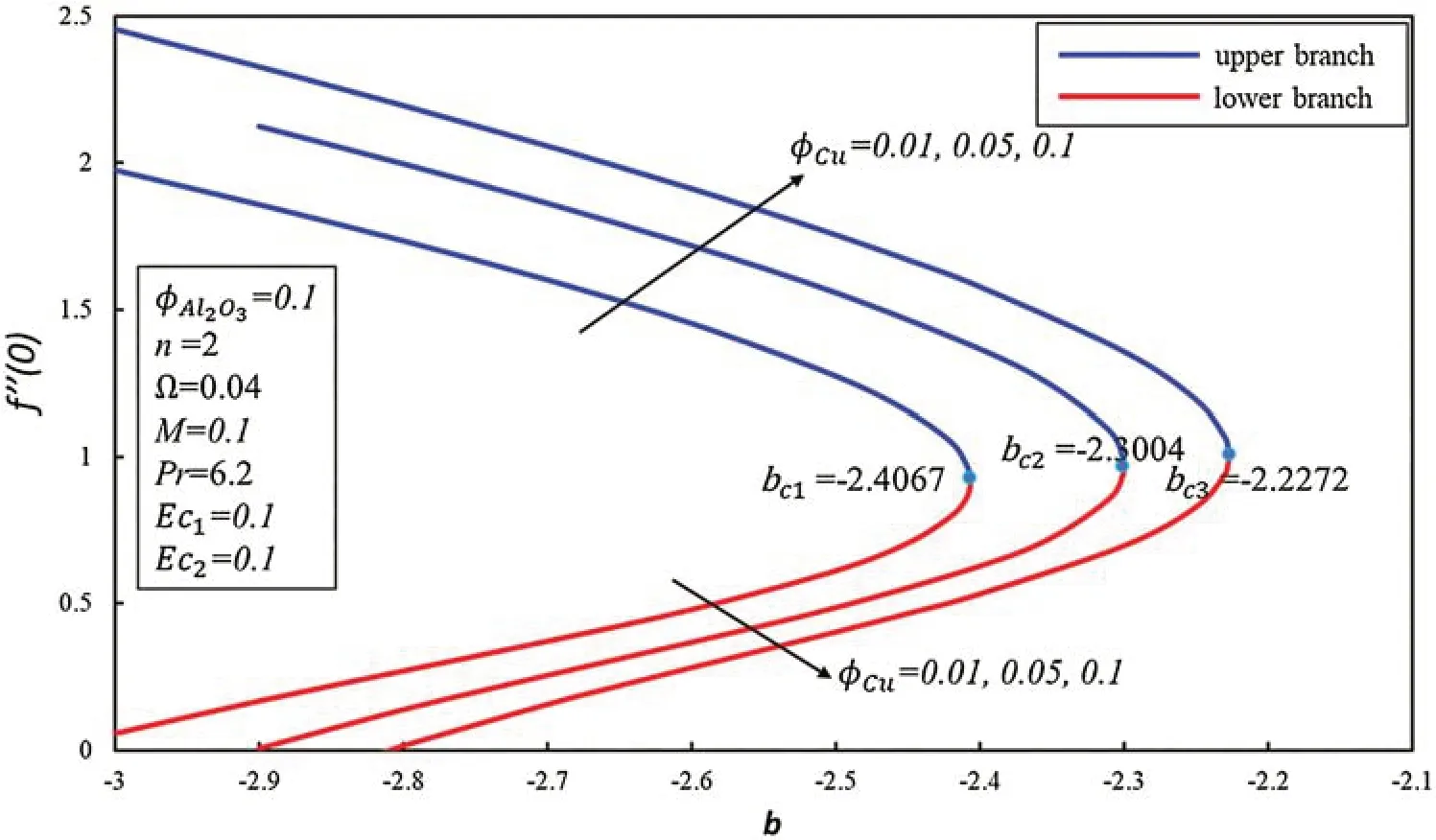
Figure 1:Effect of ϕCu on f′′(0)

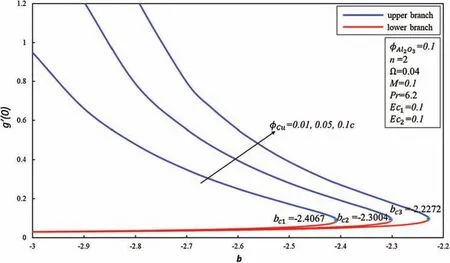
Figure 2:Effect of ϕCu on g′(0)

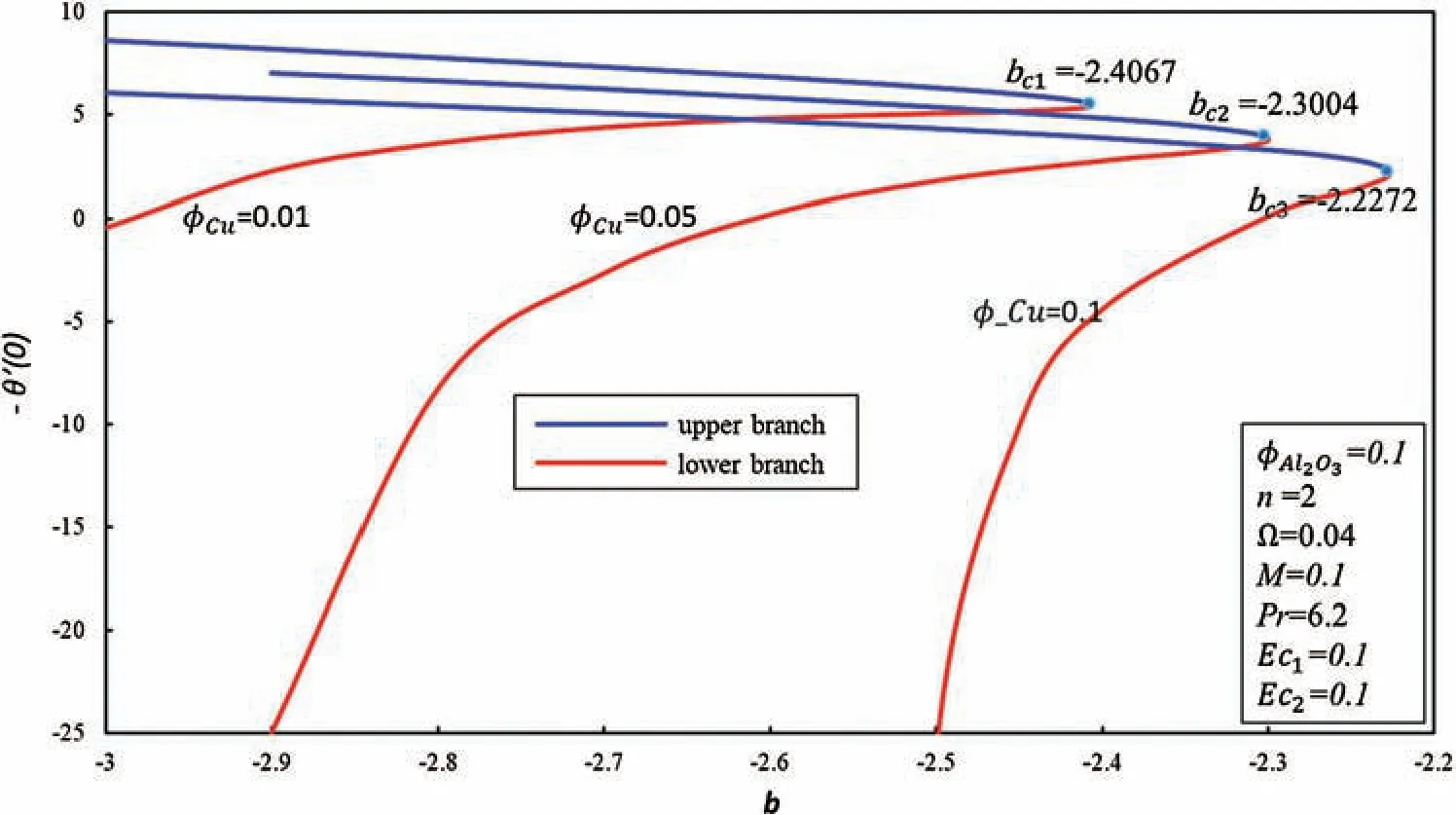
Figure 3:Effect of ϕCu on-θ′(0)

Fig.4 shows the effect ofMon profiles of velocity(f′(η),g(η))and temperature(θ(η)).It is noticed thatf′(η),g(η),and θ(η)decrease for the upper branch with the rise ofM.The result is,however,inverted in the lower branch.It should be noted that singularity exists for in the lower branch of the temperature profile when 0.1 ≤M≤0.2.Singularity indicates that the lower branch is unstable,therefore no need to perform the stability analysis in order to indicate the unstable branch.Logically,a magnetic field causes a Lorentz or drag force that involves reducing the movement of hybrid nanofluid.

Fig.5 exemplifies that how the rotation parameter Ω affects the profiles of velocity(f′(η),g(η))and temperature(θ(η)).In the upper branch,no change is noticed inf′(η)and θ(η)profiles when Ω is enhanced.When growing the rotation parameter values Ω generates higher angular velocityg(η)and higher momentum layer thickness in both branches.It should be noted that when Ω=0.1,we have obtained a single branch only.For the lower branch of θ(η),greater rotation parameter value Ω refers to the higher temperature profile θ(η),and the higher thermal layer width.

Fig.6 demonstrates that velocity(f′(η),g(η))and temperature(θ(η))of hybrid nanofluid increases by increasingnin the upper branch.However,the opposite pattern is found in the lower branch.

The effects of Eckert numberEc1andEc2on the profiles of temperature are exhibited in Fig.7.Profiles of temperature rises asEc1andEc2are enhanced for both branches.It is also noticed that the temperature of the hybrid nanofluid boosts quickly whenEc1increases as compared toEc2.

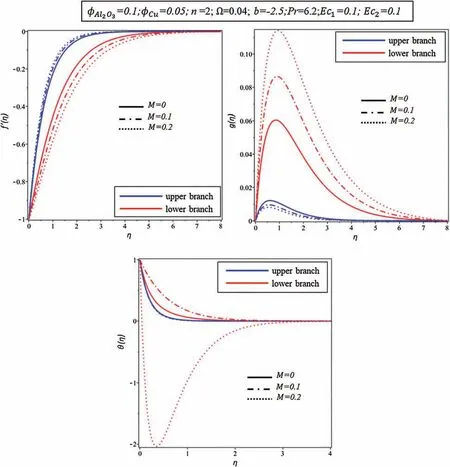
Figure 4:Effect of M on various profiles

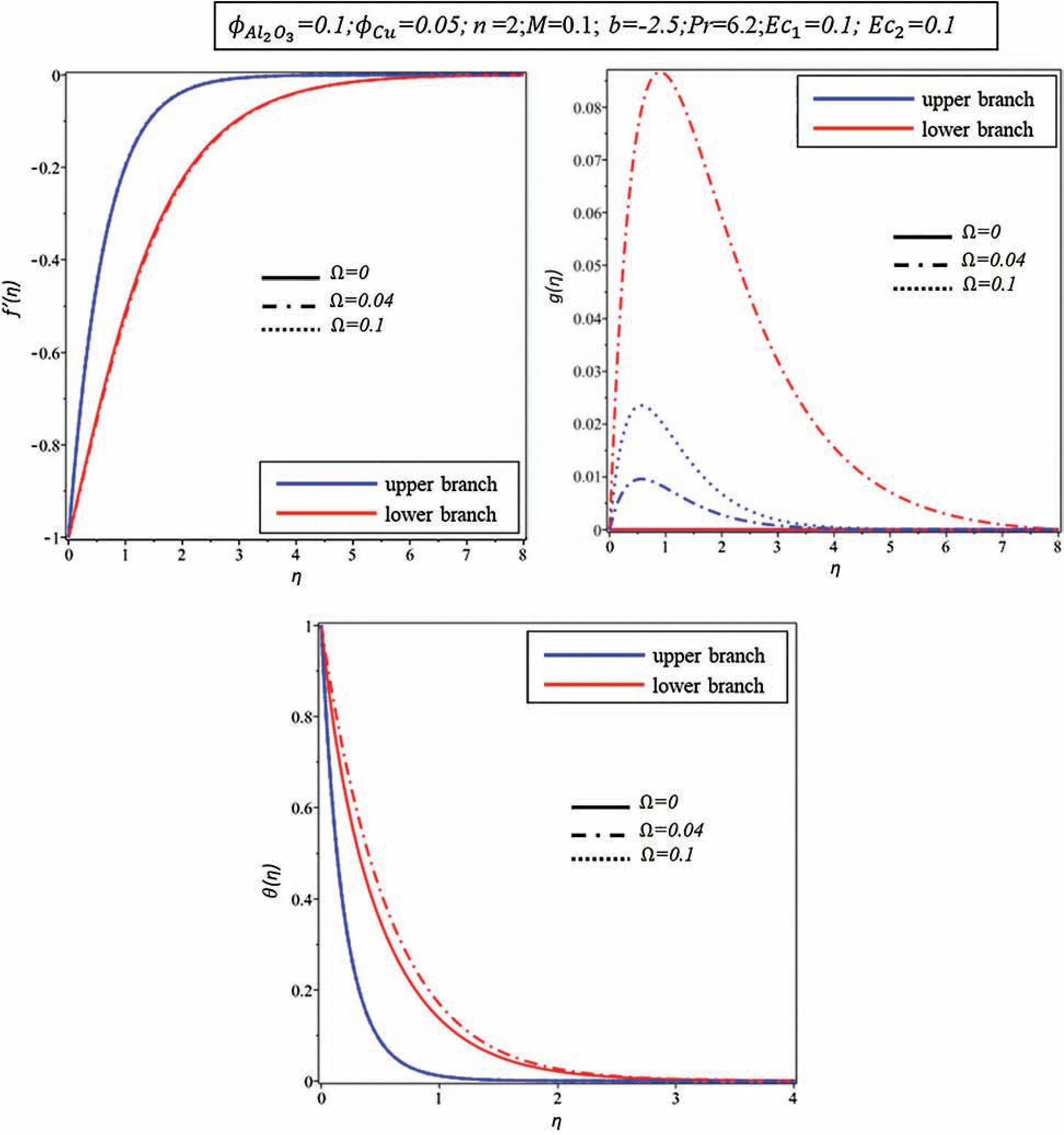
Figure 5:Effect of Ω on various profiles

Fig.8 shows the impacts of Ω on the velocityg(η)profile.The velocity profiles contain duality in nature when Ω increases.It has been found that the behavior of the velocity profile has the same behavior for the negative and positive values of the rotation(Ω)parameter.Physically,it displays that problem of hybrid nanofluid has a symmetrical solution.

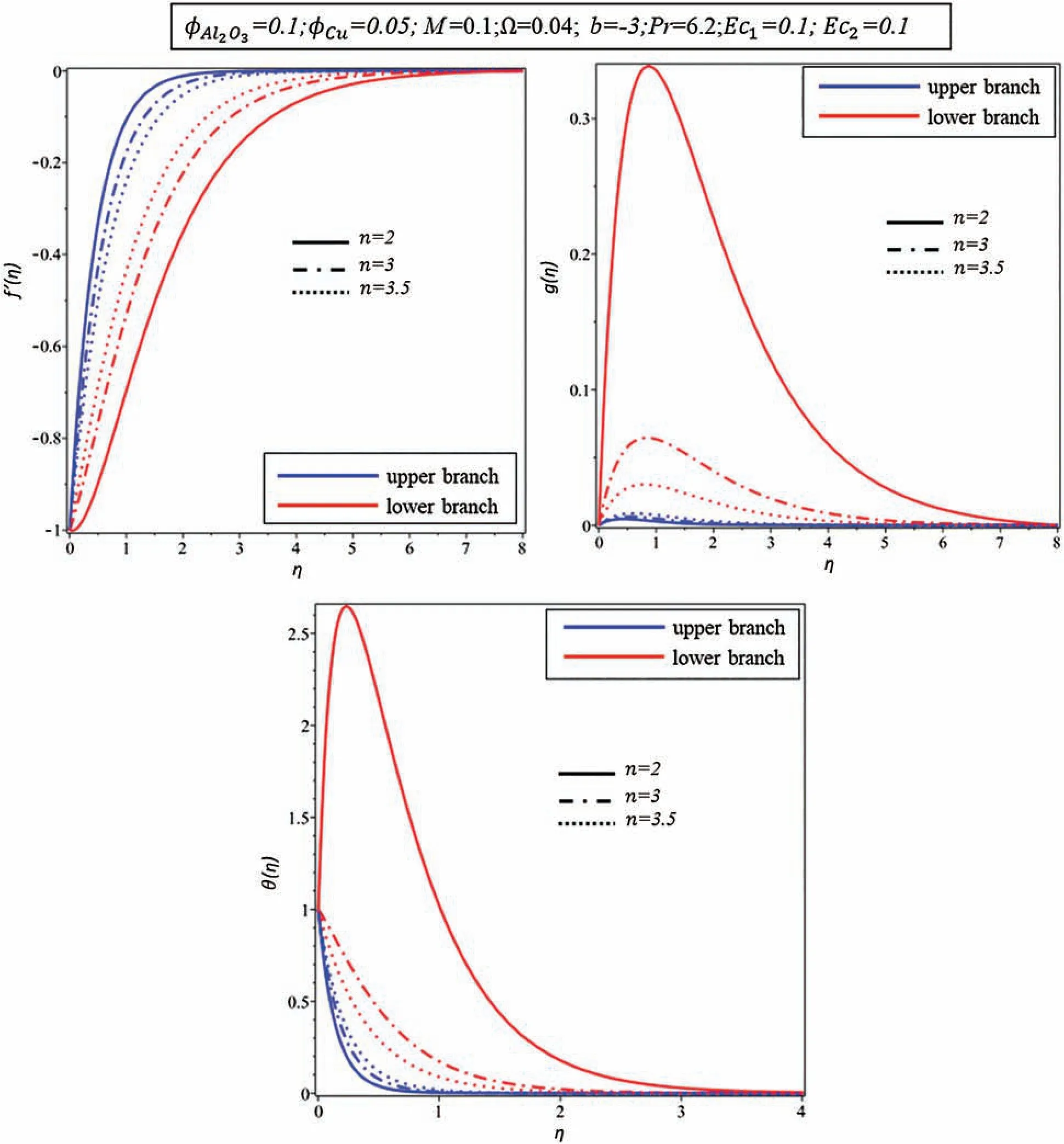
Figure 6:Effect of n on various profiles

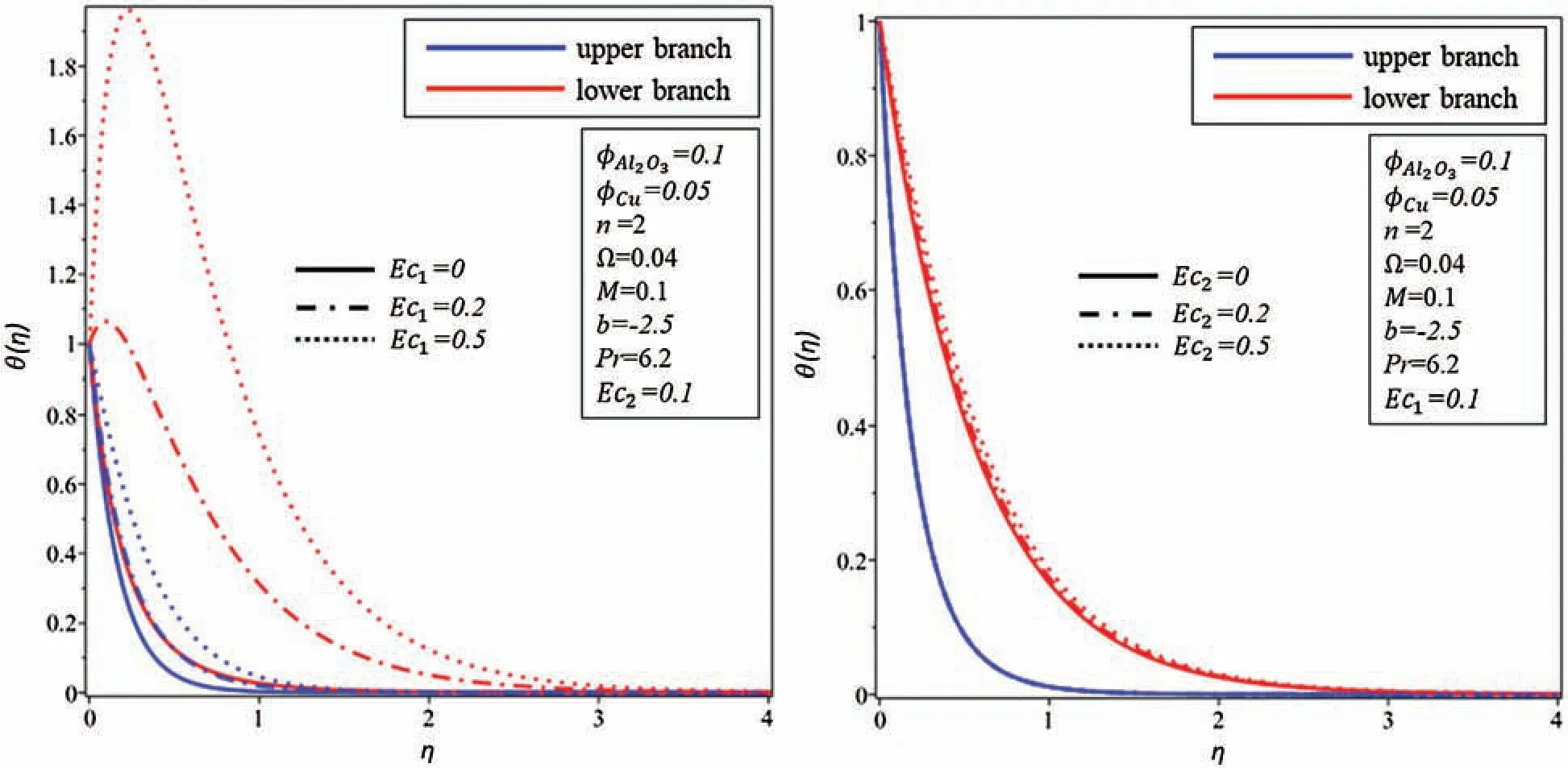
Figure 7:Effect of Eckert numbers on temperature profile

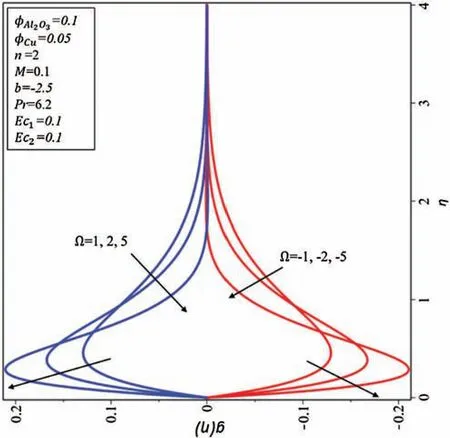
Figure 8:Effect of Ω on g (η)

4 Conclusion

In this study,we have considered the flow of rotating MHD of a water-based hybrid nanofluid on a nonlinear shrinking surface.The transformed nonlinear coupled ODEs along with BCs have been numerically examined and computed by employing ofbvp4cfunction in Matlab software.Our few main findings on this research are as follows:

1.The heat transfer rate of the hybrid nanofluid is higher than the regular nanofluid.

2.Two branches exist in the case of the higher suction.

3.Numerical outcomes indicated that branches are not unique whenb＜bc.

4.Temperature and thickness of the thermal layer increase for the higher values of the Eckert number.

5.The thickness of the thermal boundary layer reduces when the Prandtl number increases.

6.The symmetrical nature of branches exists for the solution of the angular velocity.

7.Heat transfer rate increases as the suction increases

8.Dual branches depend on the value of the rotational parameter.

Funding Statement:Researchers Supporting Project number(RSP-2020/33),King Saud University,Riyadh,Saudi Arabia.This research is also supported by Universiti Utara Malaysia.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.