深度强化学习算法分析与对比研究
2021-12-14程鑫瑶
◆程鑫瑶
深度强化学习算法分析与对比研究
◆程鑫瑶
(沈阳化工大学 计算机科学与技术学院 辽宁 110142)
随着经济社会的发展,人工智能技术也得到了快速发展,深度强化学习融入了深度学习的感知能力和强化学习的决策能力,特别是在对运动控制问题的处理上,潜力非凡。本文分析了深度强化学习算法,通过分析探寻深度强化学习在现实生产中应用的可能性。
人工智能;深度强化学习;奖励机制;经验重放;对比
近些年,因强化学习可以改善序列决策问题,受到了社会各界的广泛关注。受动物学习试错法的启发,强化学习在对智能体训练中,可以将环境和智能体融合得到的奖励值当做反馈信号。一般情况下,强化学习可用马尔可夫决策过程来表示,是由S.A.R.T.y元素构成,S特指现如今所处的环境状态,A特指智能体动作,R特指得到的奖励值,T代表状态转移的概率,y代表折扣因子。智能体策略π代表状态空间到达动作空间的映射。不断优化智能体策略,实现奖励值的最高是强化学习的核心目标。
1 深度强化学习算法分析
(1)SARSA算法
在强化学习算法中,一种相对经典的算法即SARSA算法,该算法融合了动态规划算法等特点。通过预测现阶段动作长期回报,将收集到的反馈信号上传到动作中,在获得反馈奖赏值后,智能体仅向后倒退一步,更新规则如下所示:
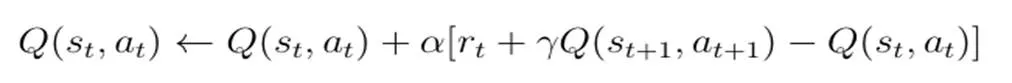
其中学习速率是,折扣因子是,在该算法中,结合当前的状态,动作值函数智能体就可明确下一个状态的动作。结合策略对值函数的依赖程度就可确定SARSA算法的收敛性,因此,对于算性性能质量来说,最关键的是设计良好的探索策略。
(2)Q-learning算法
在强化学习算法中,另一种比较经典的算法即Q-learning算法,这种算法和SARSA算法有所不同。在迭代更新中,Q-learning算法会对所有可能的动作加以考虑,在更新计算中选择最大的值函数,以下是该算法的更新规则:
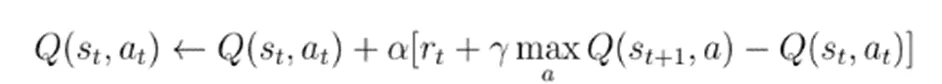
学习速率是∈(0,1],折扣因子是,该算法存在以下优点:在不考虑环境模型的基础下,对所有可用动作的预期效果加以对比。除此之外,该算法可以不做任何修改,对随机奖赏和转换问题进行处理,经理论和验证:应用Q-learning算法,针对处于有限动作和状态空间下的MDP问题,可以结合现实情况为其设计最优学习策略。
(3)确定性策略梯度算法
以下是策略梯度的计算公式:

综合以上计算公式可以知道:结构简单是确定性策略梯度计算的主要特点。一般情况下,在应用确定性策略中,会应用Actor-Critic网络来学习,在该网络架构中,在近似状态动作值函数上,要应用Critic网络,此网络学习流程和Q-learning算法非常相似。在进行网络参数学习上都是参照状态动作值函数损失函数来进行。该网络和传统的Q-learning算法有所不同的是,在计算损失函数期间,该网络不再应用贪心策略算法去选择动作,在选取未来动作时,会应用Actor网络输出动作来完成。
2 深度强化学习原理对比
常规的强化学习算法仅会对一些简单的任务环境加以处理,而实际上面临的一些任务流程都比较复杂,尤其是部分动作和状态空间是呈连续状态,应用传统的强化学习算法无法解决。随着对深度强化学习原理研究的深入发展,社会各界也越来越关注强化学习和深度学习的研究。如今人工智能领域的研究重心已集聚在深度强化学习的算法上,基于值函数近似深度强化学习算法和基于策略梯度深度强化学习算法是现阶段深度强化学习算法的两大类别,其中,前者具有典型代表的是深度 Q网络算法,后者最具典型代表的是深度确定策略梯度算法,在下文具体赘述:
(1)深度Q网络算法
在现实应用中,一些任务环境状态空间较大或者呈连续状态,想要解决这样的问题,应用直接估计离散状态动作值函数较难。通常情况下,要应用参数化连续函数对估计的状态动作值函数加以近似是常见的解决方式,算法如下所示:
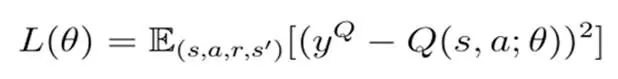
参数化连续函数Q针对一些比较复杂的环境,在近似上一般用神经网络来完成,然而强化学习算法在应用Q网络时,通常是离散的,在现实应用中不够稳定。原因是在强化学习算法期间,这些训练数据是按顺序生成的,具有较强的相关性。针对于此,外界为解决此问题,提出了DQN算法。DQN在网络输入数据上,是以原始图像为例,无需提取,本质上属于端到端的机器学习算法。该算法结合了Q-learning和深度学习算法,与传统的Q-learning算法相比,具备以下两大技术:
其一,在该算法中融合了目标网络,而应用这种目标网络可以显著提高DQN具有的稳定性。
其二,在DQN中应用了经验池结构,这种结构在训练储存期间,对应的智能体将过去应用过的数据信息加以记忆。同时,在实际应用阶段中,两个数据元组之间数据弱相关,对以往数据之间强相关性加以改善,能显著提高系统的收敛性。
(2)双重深度Q网络算法
在传统的Q-learning或DQN算法中,在选择动作并对状态动作值函数加以评估期间,会在最大化操作算子中应用相同的值,这也让实际操作中产生较高的值估计。为此,学者基于算法基础上提出了一种创新方法,此种方法也被称作双重深度Q网络算法。在应用此种算法中,最大化操作算子被分解为两大部分。
(3)深度确定性策略梯度算法
在解决连续动作空间存在的问题时,DPG虽然可以发挥一定的功能,但是一旦面临的策略网络流程相对复杂,应用此种方法依旧存在不少问题,比如具有较差的收敛性。所以学者为提高此种算法的性能,提出了深度确定性策略梯度算法。此种算法融合了DQN和DPG算法的优势,可以有效解决策略网络流程比较复杂的问题。该种算法与DQN算法一样,应用经验重放技术来提高数据应用的效率,应用这种技术,可以弱化数据之间具有的相关性,为系统学习提供充足的稳定性。在学习期间,一些需要的经验数据会被存储到经验池中,一旦经验池装满数据,会丢弃最老的数据。也会应用随机抽样的方式在经验池中抽取一些小批量的数据,将这些数据用作更新训练网络参数。与此同时,目标网络在DQN算法中应用的主要目的是提高系统具有的稳定性,而在深度确定性策略梯度算法中,在更新对应的网络参数之后,应用目标网络主要目的是及时更新滑动平均算法。
3 深度强化学习算法设计探究
强化学习属于一种有核心目的自动化学习决策的一种算法,和现有的监督学习算法有所差异,智能体在强化学习期间,并不会收到指令是否正确的命令,在优化选择和行为时,是依靠智能体得到的积极或消极的奖励来完成。随着深度学习和强化学习的有机融合,在机器学习领域,深度强化学习已将其具有的作用发挥出来。学者也积极探究深度强化学习算法的原理以及应用的途径,2015年,Lillicrap为解决机器人连续运动空间问题,指出了DDPG算法,在这之后,众多学者为提高此算法具有的性能,在此基础之上指出了事后经验重放的想法,所以陆续提出了DAPG,PPO等算法。以上算法在不同的仿真环境之下,可以将机器人运动空间问题有效解决,但是,在解决机器人面临的问题上,单纯依靠一个深度强化学习算法远远不够。究其原因,一些深度强化学习算法在控制对策以及策略形成上是逐步生成的,此种控制策略会推进机器人以较高的效率完成任务。一般情况下,电机会驱动控制机器人关节,如果电机角速度和角度轨迹波动性较大,不够稳定,也会直接影响电机的驱动力矩,甚至会引发较大的突变值,直接损害机器人的关节。所以在控制机器人运动时,应和人类运动一样,平滑地编码机械臂运动。
通过前文的分析可以看出深度强化学习算法在人工智能领域发挥着主要的功效,因此,有必要提出完善深度强化学习算法的对策,推进其在人工智能的有效应用。现如今DMPs算法在保障机器人自主学习上依旧存在问题:如何保障参数化运动基元,可以尽可能适应全新的外部环境,赋予其独立自主性。在应用运动基元过程中,通过对全局参数加以调整,可以将运动基元转化到崭新的任务模块,这里的全局参数就被称作元参数。学者在过去的研究中指出,机器模型本身决定这些元参数。例如在乒乓球活动中,当预设击球位置之后,可以通过逆运动模型得到元参数。但是实际情况是,机器人的模型结构大多处于未知,有关人员想要得到关节角度信息,无法通过逆运动来获取。因此,在提高机器人自主学习独立性上,如何应用现有的深度强化学习算法来计算和获取至关重要。为了对这种缺陷加以弥补,让机器人和人类一样可以执行任务,可以应用分层动态运动基元算法,这也是一种创新的学习算法。在该算法中,有两个相互关联的部分,即元参数以及运动轨迹,这两个部分可以独立完成训练学习,同时二者互相关联,融合了深度强化学习算法以及运动基元具有的优势,保障机器人和人类一样,不但具有自主学习能力,同时也能形成平滑的运动轨迹。
4 总结
总的来说,具备强大的感知能力,甚至在一些场景应用下已超出人类的感知水准是深度学习最大的优势,其具有深度神经网络提取原始输入的特点,如今在机器翻译、语音识别、自动驾驶等多个领域被广泛研究,并取得了显著成果。深度强化学习凭借其强大的学习感知能力,融合强化学习的理念和环境做出交融,来完成决策过程。基于此种背景之下,本文主要研究了深度强化学习的算法,并分析出深度强化学习算法的性能,为人工智能技术的发展提供必要帮助。
[1]刘全.深度强化学习综述[J].计算机学报,2018.
[2]Timothy.P.Lillic;rap.Continuous control with deep reinforc;ement learning[J].Machine Learning 2016.
[3]Volodymyr Mnih. Asynchronous Methods for Deep Rein-forc;ement Learning [J].Machine Learning 2016.
[4]董豪.基于深度强化学习的机器人运动控制研究进展[J/OL].控制与决策,2021.
[5]刘建伟.基于值函数和策略梯度的深度强化学习综述[J].计算机学报,2019.
